基于消息重要性的机会网络能量均衡路由算法

陈志刚，殷滨安，吴嘉

（1. 中南大学软件学院，湖南 长沙 410075；2.“移动医疗”教育部—中国移动联合实验室，湖南 长沙 410083）

1 引言

机会网络[1]具有间歇式连通网络[2]和延时容忍网络[3]的特征，它把节点的移动当作传输的机会，采用“存储—携带—转发”的模式进行通信。由于机会网络不需要节点间直接存在完整的链路，近年来，已经成为无线通信领域内的研究热点[4-7]。目前已经出现了基于机会网络的具体应用。例如，在手持设备交换网PSN(pocket switched network)[8]中，智能终端节点通过人们的移动提供局部通信的机会；MIT开发的CarTel[9]系统中，车辆可以通过移动与其他车辆获得局部通信的机会，或与道路旁安装的无线智能传输设备进行通信，从而将车辆传感器收集的路况和车辆状态等信息传输至 Internet上的服务器。

机会网络中的节点往往是手持或车载设备[10-11]，因此，节点间的数据传输是不稳定的，节点可能在数据传输完成前离开通信范围，导致一部分消息未能发送给对方。因此，在节点间进行数据传输的过程中，应该充分利用节点相遇的机会，优先传输重要性较高的消息。在机会网络的实际应用中，往往有一些消息是比较紧急、比较重要的。比如，在CarTel系统中，车辆故障信息要比路况信息更为重要，服务器只有收到车辆故障信息后才能采取紧急救援等措施。在手持设备交换网中，用户根据消息内容的重要程度不同，往往希望重要性较高的消息得到优先传输。

本文将节点能量和缓存空间不足等[12-13]造成传输中断的因素考虑在内，关注机会网络的实际应用中消息重要程度不同的特点，研究在机会网络单播模式下，即所有消息只有一个目的节点条件下的消息重要性度量方法，提出了基于消息重要性的机会网络能量均衡路由算法 MIEBR(message importance based energy balanced routing algorithm)，解决了重要消息得不到优先转发的问题。

2 相关工作

目前的机会网络路由算法分为零信息型和信息辅助型两大类[14]。零信息型路由算法是指在数据转发过程中不需要额外的信息作为辅助。典型的零信息型路由算法有 Direct Delivery[15]、Epidemic[16]和Spray and Wait[17]等。

Direct Delivery的特点是，源节点不通过中间节点转发消息，而是通过节点的移动，直到遇到目的节点时才传输消息。因此，网络中不存在消息副本，网络开销最小，但传输延时最大，很难提高消息投递成功率。Epidemic的思想是：在节点相遇时，互相发送对方没有的信息。这种方式在不考虑节点缓存空间和能量等因素时，消息投递成功率较高，传输延时较低。但是，在实际应用中，由于网络中存在大量的消息副本，容易造成缓存不足、网络拥塞，导致网络性能急剧下降。Spray and Wait的思想是：在Spray阶段采用喷洒的方式将源节点的信息传输给所有邻居节点。若在Spray阶段没有将消息传输到目的节点，则进入 Wait阶段，携带消息的节点通过移动直到遇到目的节点后将消息转发给目的节点。该方法解决了Epidemic消息副本数过多的问题，但由于没有利用节点和网络状态等信息，传输成功率往往不高。

由于零信息型算法没有考虑到实际应用中节点、数据及网络拓扑的特征，使该类算法往往在投递成功率、网络开销、传输延时等3个方面达不到理想平衡。而信息辅助型路由算法则是结合节点的接触历史、剩余能量、移动速度、邻居变化和社会关系等信息提出的算法。典型的信息辅助型算法有PROPHET[18]、PROPICMAN[19]和Bubble Rap[20]等。

PROPHET利用节点间的历史接触时长和接触次数信息来预测节点间的相遇概率，使消息向与目的节点相遇概率高的中间节点传递。当两个节点相遇时，它们的相遇概率增加，否则相遇概率随时间衰退。该算法同时考虑了相遇概率的传递性。相比Epidemic，该算法大大降低了路由开销，但由于未对消息副本数做出限制，随着消息的传播，网络开销依然较大。该算法未考虑到节点的社会属性，单纯依靠历史相遇概率来选择下一跳节点，存在一定的不合理性。

PROPICMAN是一个基于节点社会上下文的路由算法。其思想是：节点在转发数据时，将目的节点社会上下文信息发送给两跳以内的邻居节点，邻居节点比较自身和目的节点的社会上下文信息，并将结果返回给该节点，该节点选择两跳范围内社会上下文信息符合程度最高的邻居节点作为未来两跳的路由中转。该算法利用了社会上下文信息，在低路由开销下具有较高的消息投递成功率。但是，该算法未考虑到节点的能量对节点进行消息转发的影响，可能出现因部分节点能量消耗过快而耗尽的现象。

Bubble Rap算法通过对节点进行聚类，并计算节点的全局和局部中心度。在转发过程中，若消息没有进入目的节点所在的社区，则将消息发送给全局中心度高的节点。若消息进入了目的节点所在的社区，则将消息发送给该社区局部中心度高的节点。该算法太过于依赖中心度高的节点，造成中心度高的节点繁忙，中心度低的节点空闲，从而使网络负载不均衡。

文献[21]提出了 TBR算法，该算法结合数据分组的TTL值、跳数和数据分组大小确定消息的优先级，优先向邻居节点转发优先级高的消息。该算法减小了具有较高优先级消息的传输延时。但是，该算法在确定消息优先级时，未考虑到消息内容的重要程度。

3 模型设计

本文使用到的数学符号说明如表1所示。

表1 符号说明

3.1 节点的社会属性

网络中的每个用户节点在缓存中存储一张自身社会属性信息表，表中包含该节点用户的姓名、住址、专业、工作单位和爱好等信息。本文将这些信息称为社会上下文信息。每条信息包括属性名(attriName)和属性值(value)。为方便节点间进行属性值的比较，同时保护用户的社会上下文隐私，每个属性值映射为长度固定的散列值(hashvalue)，并且保证网络中的每一个用户节点具有相同的属性名和相同的排序。节点的社会属性信息如表2所示。

表2 社会属性信息

节点的第i项社会属性散列值H(wi)是由属性值wi映射得到的长度为32 bit的十六进制数，是数据唯一且极其紧凑的数值表示形式。本文采用MD5对wi进行映射。

例如，属性名为爱好，属性值为乒乓球，则H(乒乓球) 的值为32 bit的十六进制数且是唯一的571c4d3c50312404d3c82b8dc02e2805。

定义节点a与节点b的社会关系强度为

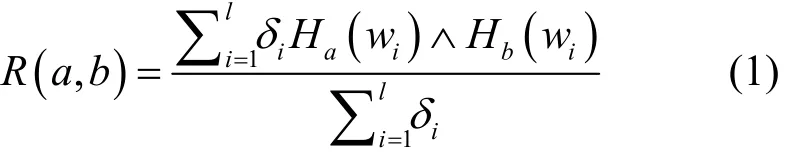
其中，用 δi∈(0,1)来区分不同属性的重要程度，δi越大，表示该项属性越重要。Ha(wi)表示节点a第i项属性的散列值，l为节点社会属性数，∧为逻辑与运算。由于每个节点的属性个数和顺序相同，因此只需要l次比较就可以得到R(a,b)。当两节点所有属性值都相同时，即对于i∈[1,l], 有Ha(wi)∧Hb(wi) ≡1，则Rmax(a,b)= 1 。对于i∈[1,l]，当Ha(wi)∧Hb(wi) ≡ 0 时，则Rmin(a,b) =0。所以，R(a,b)的值域为[0,1]。

3.2 消息重要性的度量

消息的重要性由两方面共同决定：1) 消息内容的重要程度，由消息发送方决定；2) 由消息的TTL值、跳数和大小决定。由此，定义消息m的重要性度量值为

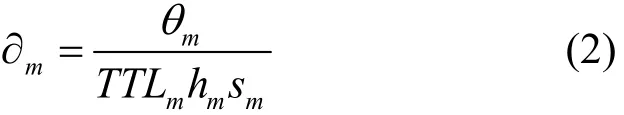
其中，θm表示消息发送方根据m的内容重要程度而设定的值， θm∈(0,1)，θm越大表示m的内容越重要。TTLm为m的剩余生存时间。需要注意的是，不同于TCP/IP协议中的TTL，TCP/IP协议中的TTL表示的是消息可转发的最大跳数，机会网络中的TTL表示的是消息的剩余生存时间。TTL值越小，表明消息离被删除的时间越近，越需要被优先转发。hm为m的跳数，hm越小，表明该消息被转发的次数越少，越需要尽快转发。sm为m的大小，sm越小，则m中每比特的消息重要程度越大。

3.3 消息的缓存价值

机会网络中的节点缓存空间是有限的，当传输过程中接收方缓存不足时，需要删除缓存中的部分消息，从而保证节点具有足够的缓存空间接收数据。从缓存中删除的消息，应该具有最低的缓存价值。

定义消息的缓存价值为

其中，TTLm越小，消息m被转发过的概率越大。反之，TTLm越大，表明消息m被转发的概率越小，则消息m越需要被优先保留。特别地，当TTLm减为0，说明该消息已超过其时效期限，缓存价值为0。mθ越大，即消息m的内容越重要，缓存该消息的价值也就越大。

3.4 能量消耗模型

机会网络中的节点往往是移动设备，这些节点的能量是有限的。因此，必须考虑节点能量对消息转发的影响。

一个数据分组在由节点a转发至节点b的过程中的能量消耗，主要包括节点a转发一个数据分组所消耗的能量ES，以及节点b接收一个数据分组所消耗的能量ER和返回ACK给节点a所消耗的能量EACK。由此，建立节点的剩余能量模型。

设消息m的字节数为Bm，一个数据分组的字节数为Bpkt，则节点a转发m后的剩余能量为

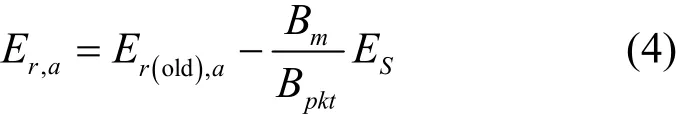
节点b接收m后的剩余能量为

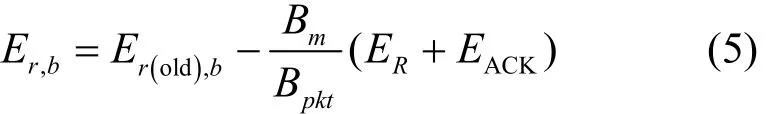
其中，Er(old),a表示节点a转发m前的剩余能量，Er(old),b表示节点b接收m前的剩余能量。

定义节点a的剩余能量百分比为

其中，Emax为节点的最大能量值。

本文关注的是节点在传输消息的过程中的能量消耗，不考虑节点能量衰减等其他因素。

3.5 节点转发消息的收益

节点a在转发消息m至节点b时，若节点b是消息m的目的节点，则节点a转发消息m的收益只由消息m的重要性度量值∂m决定。

若节点b不是消息m的目的节点，则不能只凭消息重要性度量值来确定消息的转发顺序。显然，节点转发重要性较高的消息并成功投递到目的节点，要比重要性较低的消息的成功投递具有更高的收益。但是，若重要性较高的消息未能成功投递到目的节点，则节点的收益为 0。同时，为均衡网络中各节点的剩余能量，延长网络的生命周期，需要将消息转发给剩余能量较多的节点。

由此，定义消息m由节点a转发至节点b的收益为

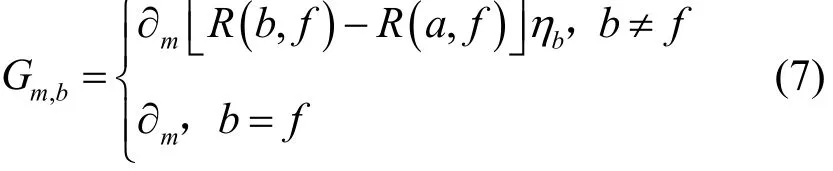
其中，消息m的目的节点为f。ηb表示节点b的剩余能量百分比。由基于社会上下文路由算法的有效性可知，与目的节点的社会上下文信息越相似，则节点与目的节点的相遇概率越高，消息投递成功率也就越高。因此，用R(b,f)-R(a,f)表示消息投递成功率的增量。

图1给出了节点转发消息的实例。节点a有两条消息需要转发给节点b，节点b不是这两条消息的目的节点。设 ηb=0.8，按照式(7)计算得Gm1,b= 0 .064，Gm2,b= 0 .192。由此可见，虽然∂m1＞∂m2，但因Gm2,b＞Gm1,b，节点a应该优先选择m2进行转发。

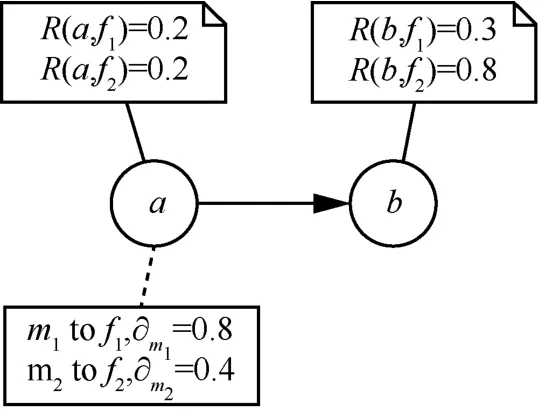
图1 节点转发消息的实例

4 MIEBR设计

部分节点能量的过快消耗降低了网络生命周期。在路由选择时，结合消息重要性和节点能量因素设计路由策略，可均衡节点的能量消耗。结合消息缓存价值设计节点缓存替换策略，可高效利用缓存空间。本章首先设计能量均衡路由策略，然后设计缓存替换策略，最后给出相应的伪代码并分析算法的开销。

4.1 能量均衡路由策略

为了方便描述，记节点缓存中待转发的消息集合为M= {m1,m2,… ,mu}，记M中目的节点地址集合为F= {f1,f2, … ,fd}，记当前时刻下的邻居节点集合为V= {v1,v2,… ,vk}。下面描述能量均衡路由策略的具体步骤。

步骤1网络初始化。当节点加入网络时，将自己的社会上下文信息和地址进行广播，并请求其他节点的社会上下文信息和地址。根据式(1)计算出节点与其他节点的社会关系强度，并存储在缓存中。

步骤2节点a将F发送至{b|b∈V} 中的每个邻居节点，并与邻居节点相互发送消息汇总矢量SV(summary vector)。{b|b∈V} 中的每个邻居节点将步骤1中计算得到的{R(b,f)|f∈F}，以及ηb发送给节点a。

步骤3节点a确定消息的转发顺序和下一跳节点。对于中的每一条消息，执行以下步骤。

① 在每个邻居节点的消息汇总矢量SV中查找当前消息mi，记没有当前消息mi的邻居节点集为V0，对于 {b|b∈V0}中的每个邻居节点，分别根据式(7)计算得到Gmi,b，取其中的最大值作为当前消息mi的转发收益值Gm，即

若Gmi≤ 0 ，则不转发该消息。② 取使Gmi达到最大值的邻居节点作为当前消息mi的下一跳节点。因为使Gmi达到最大值的邻居节点可能不止一个，因此记为节点集V*，即

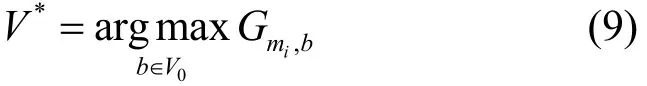
步骤4节点a按照消息转发收益值由大到小的顺序依次向步骤 3中确定的下一跳节点转发消息。若出现消息转发收益值相同的情况，则依据消息在缓存中的起始地址由低位到高位的顺序确定消息转发的优先级。若下一跳节点为消息的目的节点，则下一跳节点在收到消息后以广播的方式向网络中发送接收确认ACK分组，网络中各节点在收到接收确认ACK分组后在本地缓存中查找该消息，若缓存中存在该消息，则将该消息删除。每条消息的转发过程在消息传输完毕或传输链路中断后结束。每条消息转发过程结束后，消息转发节点和接收节点分别按式(4)和式(5)更新节点的剩余能量信息。

步骤5节点a维护邻居节点集V。节点a于每个周期T广播Hello分组，Hello分组用来发现新的邻居节点和确认邻居节点是否离开通信范围。邻居节点若收到Hello分组，则向节点a回复Hello的ACK分组。若节点a发现新的邻居节点，则将其加入V中。若节点a未收到邻居节点回复的Hello的 ACK分组，则可认为该邻居节点不在通信范围内，将其从V中删除。若邻居节点集V有变动，则根据式(8)、式(9)更新缓存中消息转发的顺序和消息的下一跳节点。

下面结合具体的例子描述能量均衡路由策略的消息转发过程。图2中，节点a当前的邻居节点为b和c，节点a缓存中有两条消息m1和m2待转发。对于消息m1，根据式(7)计算Gm1,b=0.1，Gm1,c= 0 .1，则根据式(8)知Gm1= 0 .1。对于消息m2，可得Gm2,b=0.02，Gm2,c= 0 .08，则Gm2= 0 .08。由Gm1＞Gm2可知，消息转发顺序为m1,m2。由式(9)可知，因为Gm1=Gm1,b=Gm1,c，则将m1转发至节点b和c，因为Gm2=Gm2,c，则将m2转发至节点c。

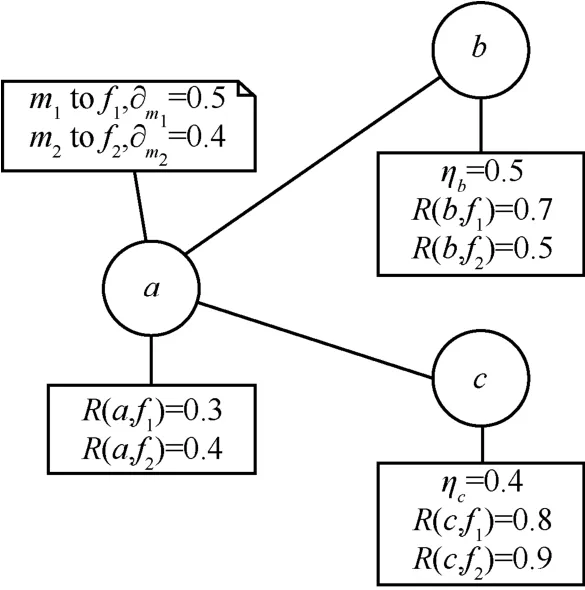
图2 能量均衡路由策略消息转发过程实例

4.2 缓存替换策略

节点b接收消息m前，比较m的大小sm与节点b的剩余缓存空间SL的大小。若sm≤SL，则节点b接收m；若sm＞SL，则节点b由于剩余空间不足不能直接接收m，但节点b可以将缓存价值较小的消息进行丢弃，满足sm≤SL的条件后再接收m。由此，建立0-1背包问题模型。

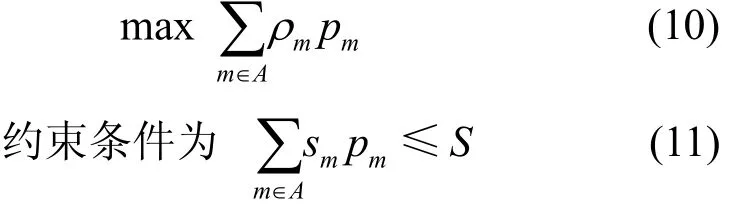
其中，pm∈ { 0 ,1}，当m存入缓存中时，pm=1，否则，pm= 0 。

0-1背包问题是一个NP难题，可以使用动态规划、记忆化搜索等算法求得该问题的精确解，但考虑到时间和空间复杂度，求精确解的方法是不实用的，本文采用修复法[22]求该问题的近似解。下面描述缓存替换策略的具体步骤。

1)D=∅，D表示从A中删除的元素集合。

2) 查找A中 ρm/sm最小的一条消息，记为mmin；若结果为空，则算法结束。

3)A=A {mmin}，D=D∪{mmin}。

4) 若SA＞S，则转到步骤 2)；否则，说明缓存装得下A中所有的消息，此时查看消息m在不在D中，若m∈D，则算法结束。若m∉D，则执行C=CD，C=C∪{m} ，即删除缓存中属于D的消息，然后整理缓存空间，将缓存空间中的消息紧凑排列后，把m存入缓存中。

下面结合具体的例子描述缓存替换策略。图3(a)描述了当前缓存的状态，缓存中的消息为m1，m2和m3，此时m4待存入缓存，这4条消息按照 ρm/sm由大到小的排序依次为m1,m2,m4,m3。按照缓存替换策略，，此时并不真正从缓存中删除m3，如图3(b)所示。

此时比较SA和S的大小，分两种情况分别讨论。第一种情况为若SA＞S，则因为m4∈D，所以算法结束，缓存中不删除任何消息。第二种情况为若SA≤S，因为m4∉D，则删除缓存中的m3，如图3(c)所示，因为剩余缓存空间不连续，此时缓存还是存不下m4，必须对缓存消息进行整理，将消息紧凑排列后再存入m4，如图3(d)所示。

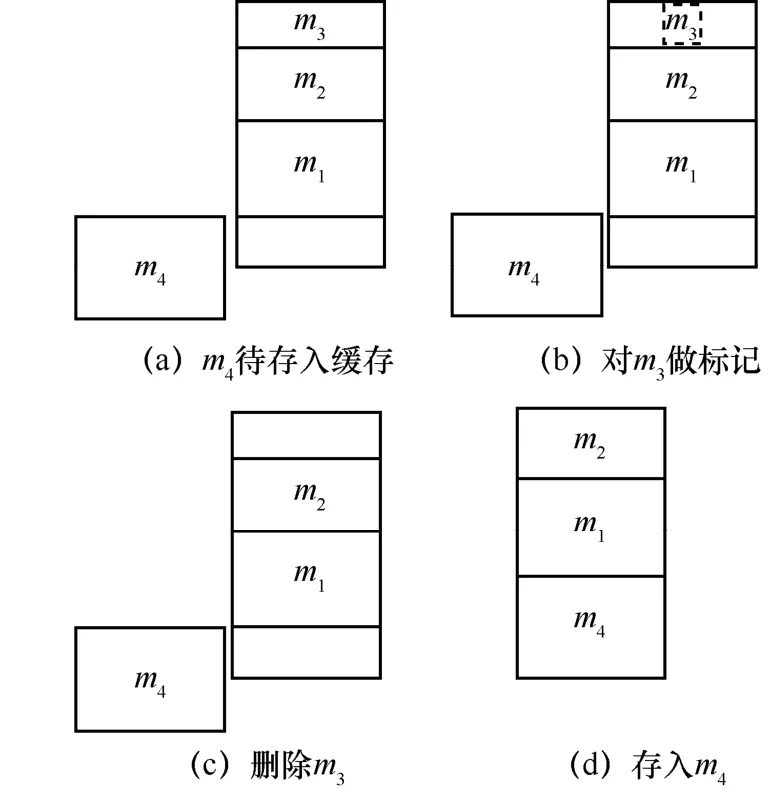
图3 缓存替换操作实例

4.3 算法伪代码

根据以上的分析，MIEBR的思想可用如下伪代码描述。

4.4 复杂度分析

MIEBR虽然提高了节点转发消息的收益，均衡了节点的能量消耗，高效利用了节点的缓存空间，但也带来了额外的开销，一定程度上降低了消息的剩余生存时间。下面分析MIEBR的时间复杂度、空间复杂度和通信复杂度。

1) 时间复杂度

MIEBR在初始化时，需计算节点间的社会关系强度，设网络中节点数为N，节点社会属性数为l，计算两节点间社会关系强度的时间复杂度为O(l)，每个节点需要计算与N-1个节点的社会关系强度，则时间复杂度为O(Nl)。在计算消息的转发收益时，需要查询k个邻居节点的消息汇总矢量SV。因为消息汇总矢量SV的第x位用0或1代表该位置对应的消息分组在缓存中不存在或存在，所以，查询一次消息汇总矢量SV的时间消耗仅为O(1)。缓存中共有u条消息，则计算节点缓存中所有消息的转发收益的时间复杂度为O(uk)。节点按消息转发收益大小确定消息转发顺序，排序算法采用归并排序，时间复杂度为O(ul ogu)。缓存替换算法中的时间开销主要用于遍历A，时间复杂度为O(n)。

2) 空间复杂度

节点存储自身的社会上下文信息需要的空间开销为O(l)。网络中的每个节点计算与其他节点的社会关系强度值后，需要存储在缓存中，空间复杂度为O(N)。节点存储k个邻居节点发送的消息汇总矢量SV，设一个消息汇总矢量SV的长度为q，则空间复杂度为O(kq)。节点存储消息的下一跳节点地址、消息重要性度量值和消息转发收益值，需要空间为O(u)。采用归并排序确定消息的转发顺序，辅助空间仅为O(1)。

3) 通信复杂度

通信复杂度是指MIEBR中传输控制消息的开销，不包括传输数据消息的开销。MIEBR传输控制消息的开销主要来源于向邻居节点发送的消息目的地址集F以及消息汇总矢量SV，则通信开销为O(d+q)，以及邻居节点返回的社会关系强度值和消息汇总矢量SV，也为O(d+q)。

5 仿真与分析

本文使用 ONE(opportunistic network environment)[23]对MIEBR进行仿真实验，比较MIEBR与典型路由算法 Epidemic、PROPHET以及PROPICMAN的性能。为了更加真实的模拟现实生活中人们的移动规律，本文选择芬兰首都赫尔辛基地图，采用Working Day Movement模型[24]进行仿真，仿真运行 10次后取平均值作为最终的结果。设置消息产生时的θ值在(0,1)上服从均匀分布。具体仿真参数设置如表3所示。

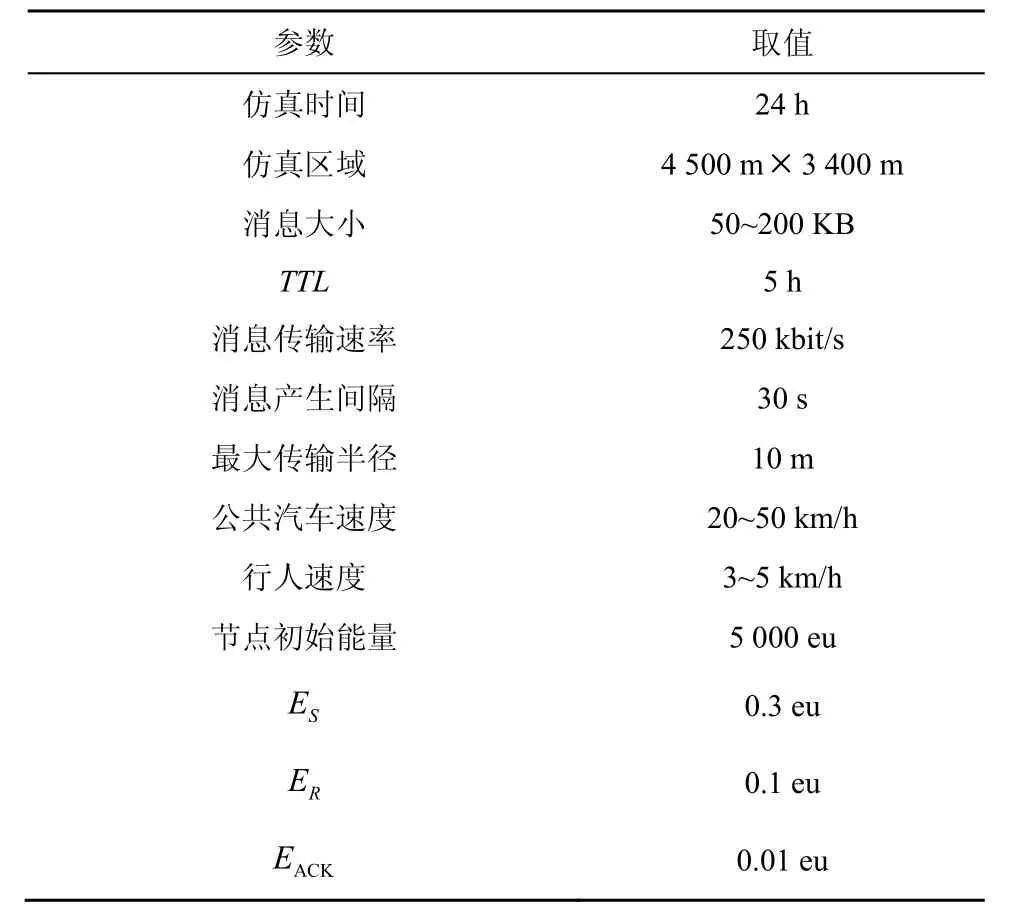
表3 仿真参数设置

5.1 能量均衡性能

本文用以下指标衡量算法的能量均衡性能。

1) 节点死亡收敛速率。用tα表示在死亡节点数量所占比率为α下的网络运行时间。在一定的α下，tα越大，表示节点的平均生存时间越大。定义节点的死亡收敛速率为

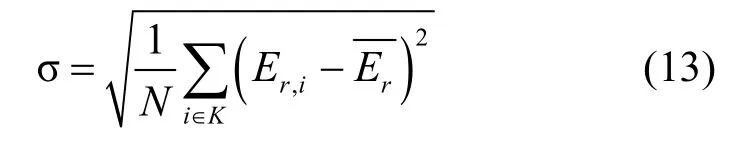
设置网络中节点数量为 260个，缓存大小为30 MB，网络中死亡节点比率从0.1上升至0.5期间，每隔0.1的比率记录不同算法的网络运行时间。网络运行时间从1 h到7 h，每隔1 h计算不同算法的节点剩余能量标准差。

由图4可知，随着死亡节点比率的增大，网络运行时间都会有所增加，MIEBR的网络运行时间最大，这是因为MIEBR控制了消息副本数量，传输消息次数较少，同时均衡了节点的能量消耗。MIEBR的网络运行时间的增加最为缓慢。通过式(12)的计算，当死亡节点比率从0.1变化到0.5时，MIEBR、PROPICMAN、PROPHET以及Epidemic的φ值依次为 9 .3× 1 0-5、 2 .8× 1 0-5、 3 .0× 1 0-5和 3 .6× 1 0-5，表明MIEBR具有最快的节点死亡收敛速率，能量均衡性能最好。

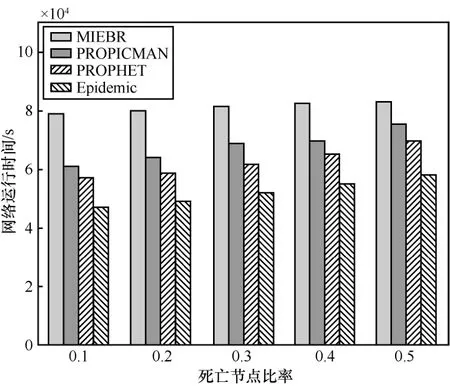
图4 不同死亡节点比率下的网络运行时间

死亡节点比率从α变化到β时，φ越大，表示节点的死亡收敛速率越快，能量均衡性能越好。

2) 节点剩余能量标准差。节点剩余能量标准差体现了节点之间的剩余能量差异的大小，节点剩余能量标准差越小，表示能量均衡性能越好。节点剩余能量标准差为

由图5可知，随着网络运行时间的增加，不同算法的节点剩余能量标准差都有所增加，MIEBR的节点剩余能量标准差最小，表明MIEBR的节点剩余能量分布相比之下更加均匀。这是因为MIEBR在路由的选择时，结合了邻居节点的剩余能量比率，避免了转发能力较强节点能量的过快消耗而导致节点剩余能量差异过大的现象。

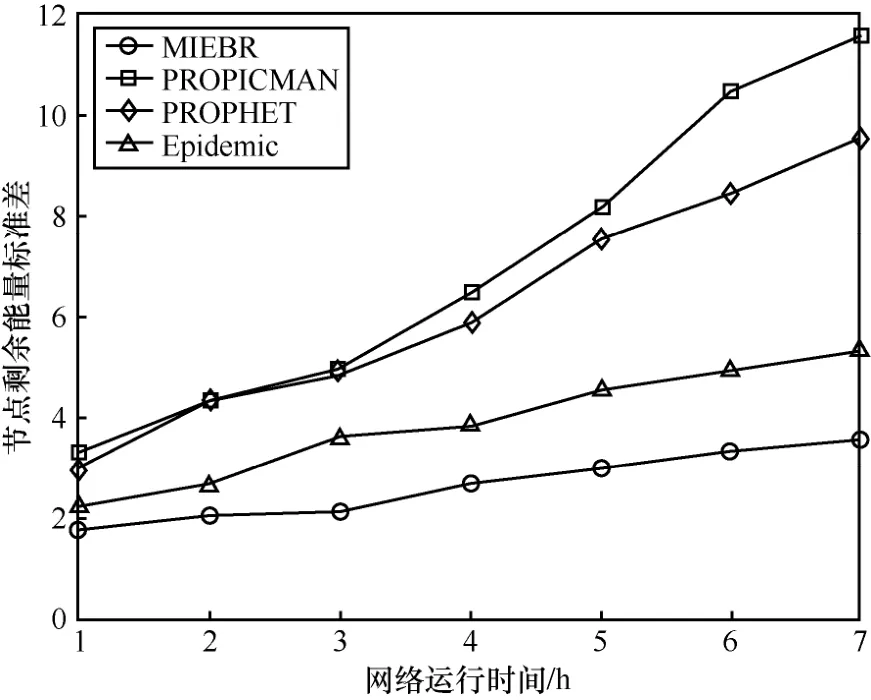
图5 不同网络运行时间下的节点剩余能量标准差

5.2 节点数量对算法性能的影响

节点数量的增加使节点间相遇次数增多。本节设置节点缓存空间为30 MB，随着节点数量的增加，比较在不同的θ区间下 MIEBR的平均消息延时，比较MIEBR、PROPICMAN、PROPHET和Epidemic的消息投递成功率、平均消息延时和网络开销比率。

图6显示的是MIEBR在不同的节点数量和不同的θ区间下的平均消息延时。从图6中可知，不同θ区间的平均消息延时都随着节点数量的增加而减小，θ值越大，则具有越低的平均消息延时。这是因为θ值越大，则消息重要性度量值就越大，在消息转发和缓存替换中具有较高的优先级 。 θ ∈ ( 0.75,1)的 平 均 消 息 延 时 分 别 比平均降低了4%，9%和14%。

图7显示的是不同节点数量下的消息投递成功率。从图7中可知，MIEBR有着最高的消息投递成功率，而Epidemic投递成功率最低，并从节点数量为200以后开始下降。这是因为Epidemic的消息副本数最多，导致了缓存空间不足和能量的过快消耗，当网络中较多的节点死亡后，投递成功率将大幅下降。而MIEBR不但具有节点剩余能量均衡策略，还具有缓存消息替换策略，很好地解决了节点剩余能量不均衡和缓存空间利用不充分的问题。MIEBR的消息投递成功率分别比 PROPICMAN、PROPHET和Epidemic平均提高了23%、31%和52%。

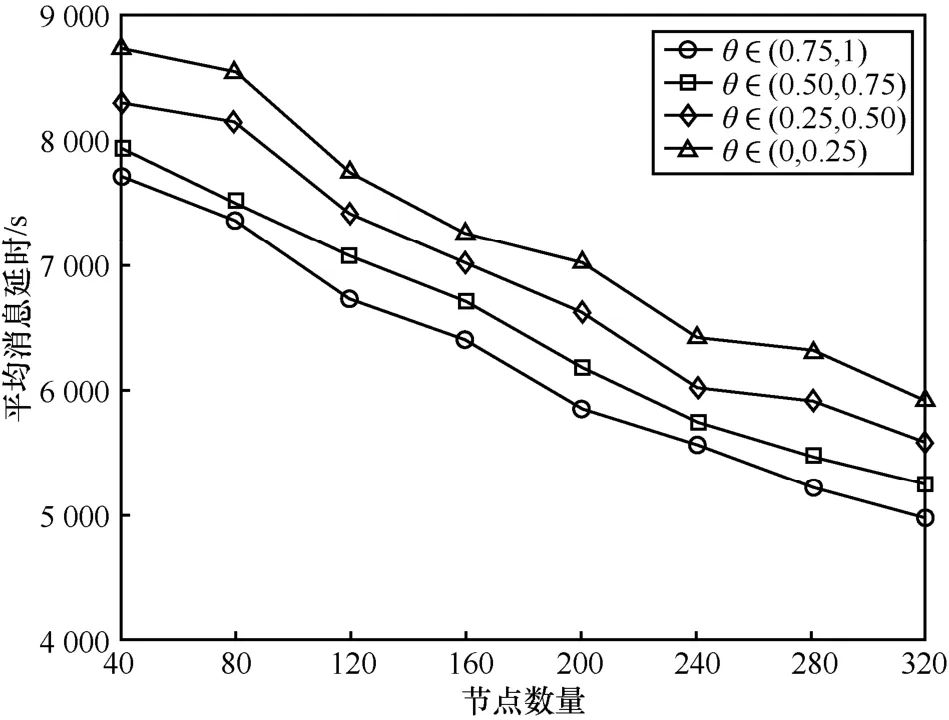
图6 不同θ区间下的平均消息延时

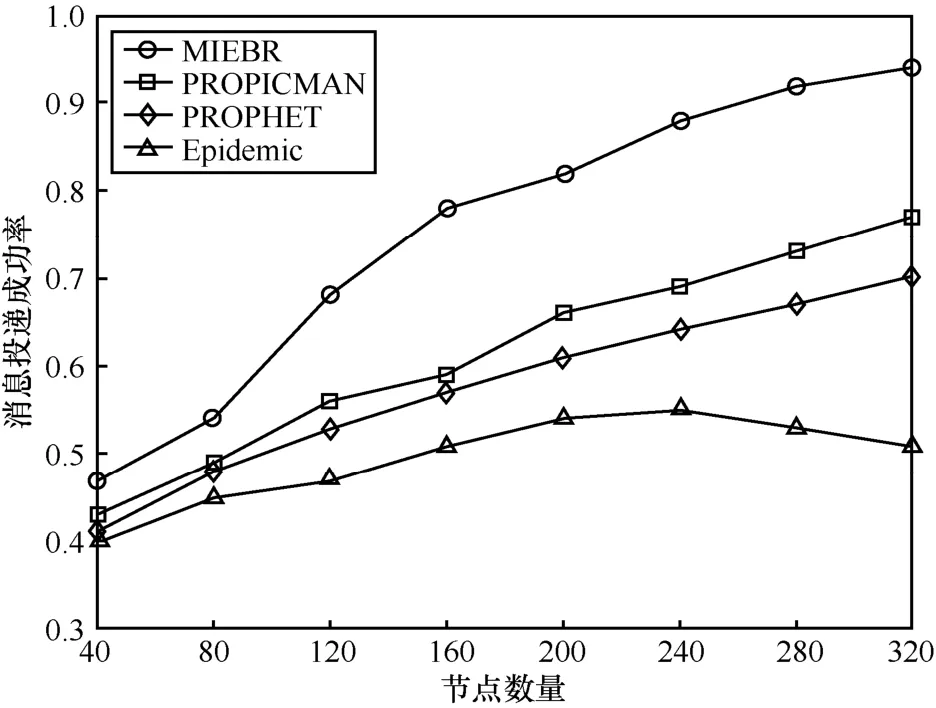
图7 不同节点数量下的消息投递成功率

图 8显示的是不同节点数量下的平均消息延时。从图 8中可知，MIEBR、PROPICMAN和PROPHET的平均消息延时都随着节点数量的增加而快速下降。Epidemic的平均消息延时最高，并且先下降后增加。这是因为随着节点数量的上升，节点相遇次数的增加导致了传输次数增多，使节点能量消耗过快，节点的过快死亡导致了平均消息延时的上升。同时，Epidemic大量的消息副本造成了缓存空间不足，影响了消息的接收和转发。MIEBR的平均消息延时最低，且与PROPICMAN较为接近。MIEBR的平均消息延时分别比PROPICMAN、PROPHET和 Epidemic平均降低了2%、8%和19%。

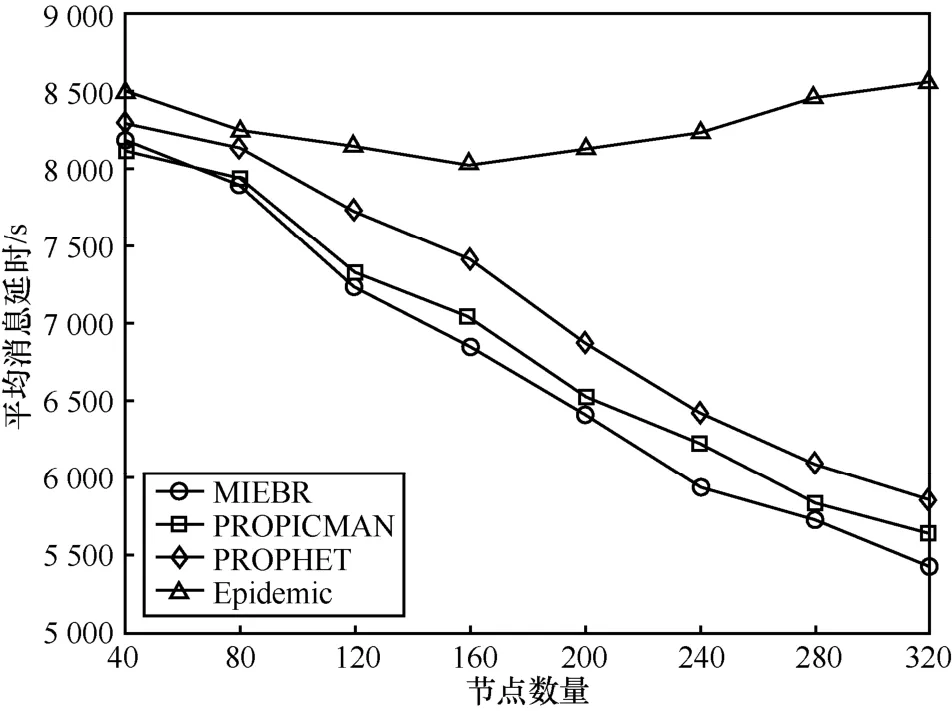
图8 不同节点数量下的平均消息延时

图 9显示的是不同节点数量下的网络开销比率。从图9中可知，网络开销比率都随着节点数量的增加而上升。Epidemic的网络开销比率最高，而且上升趋势最明显。这是因为Epidemic没有控制消息副本的数量。MIEBR和PROPICMAN的网络开销比率相差不大，并且都比 PROPHET的要小。这是由于这两种算法只选择最佳的邻居节点转发数据，有效控制了网络开销。MIEBR的网络开销比率分别比Epidemic和PROPHET平均降低了70%和36%。

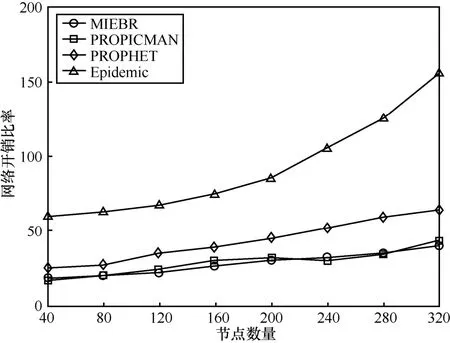
图9 不同节点数量下的网络开销比率

5.3 缓存空间对算法性能的影响

节点缓存空间的大小是影响算法性能的一个重要的因素。缓存空间越大，则节点可存储转发的消息越多。本节设置节点数量为280个，研究缓存空间的变化对算法性能的影响。

图 10描述了不同缓存空间下的消息投递成功率。从图10中可知，4种算法的消息投递成功率都随着缓存空间的增加而上升。MIEBR具有最高的消息投递成功率。

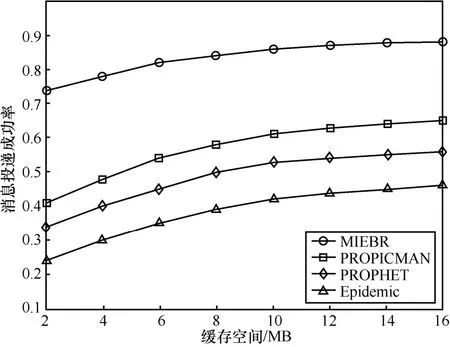
图10 不同缓存空间下的消息投递成功率

图11描述了不同缓存空间下的平均消息延时。从图 11中可看出，平均消息延时随缓存空间的增加而下降，Epidemic具有最高的平均消息延时，且下降趋势最为明显。MIEBR具有最低的平均消息延时，且变化较为平缓。

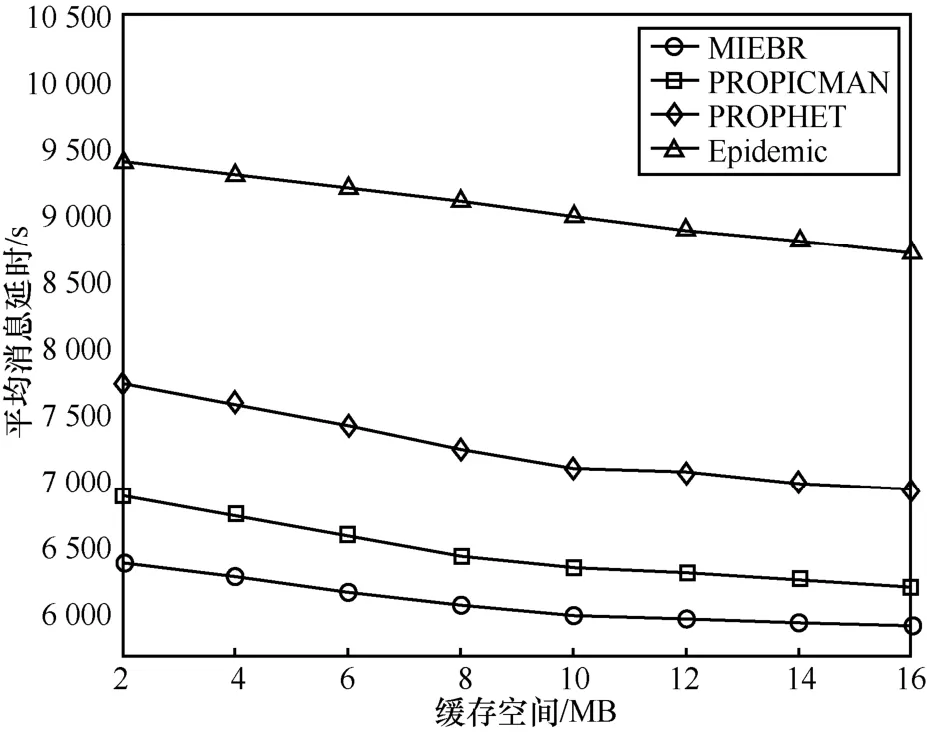
图11 不同缓存空间下的平均消息延时

图12描述了不同缓存空间下的网络开销比率。随着缓存空间的增加，4种算法的网络开销比率都不断下降。Epidemic的网络开销比率下降趋势最为明显，MIEBR和PROPICMAN的网络开销比率基本相同且下降趋势较为平缓。

由以上结果可知，节点缓存大小一定程度上影响了算法的性能。在相同的网络环境下，缓存空间越大，则节点可携带的消息越多，当遇到其他节点时，转发的消息量也就越多，因此，消息投递成功率越高，平均消息延时越低。在数据转发的过程中，若邻居节点缓存不足，PROPICMAN、PROPHET和Epidemic只能等待该邻居节点因缓存中消息的TTL值减为0被删除或该邻居节点收到目的节点接收确认的ACK释放出缓存空间后，继续进行数据传输。因此，未采用缓存替换策略的PROPHET、PROPICMAN和Epidemic算法性能受缓存空间因素影响较大。而 MIEBR由于采用了缓存替换策略，使该算法在缓存空间不足时仍具有较好的性能。

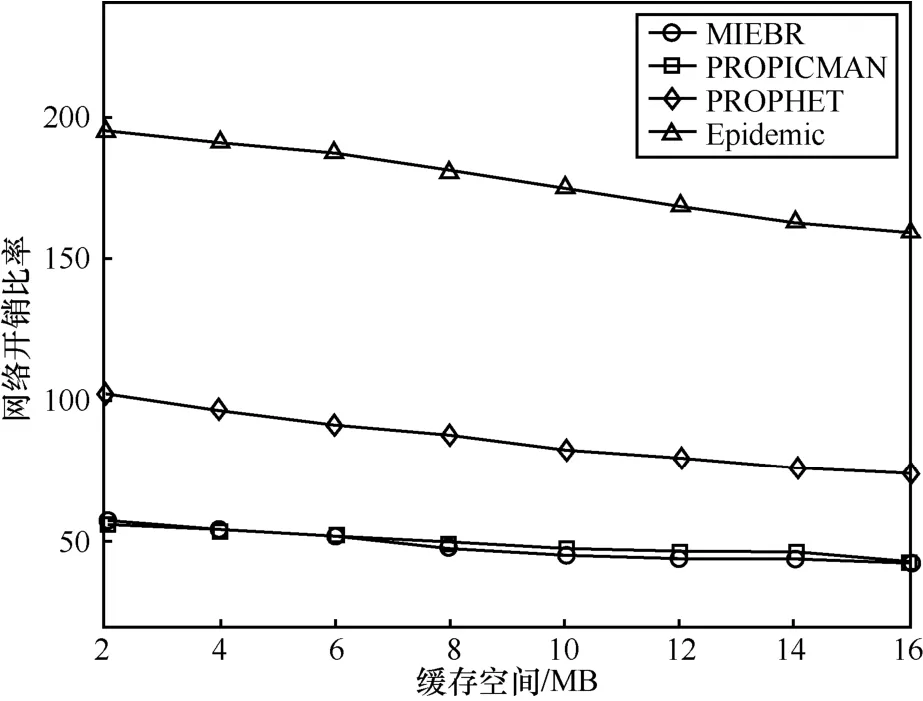
图12 不同缓存空间下的网络开销比率

6 结束语

本文提出的 MIEBR通过引入节点用户对消息内容重要程度的设定，提出了消息重要性的度量方法；依据消息的缓存价值，设计了缓存替换策略；根据节点转发消息的收益，设计了能量均衡路由策略。MIEBR提高了节点转发消息的收益和缓存利用率。实验结果表明，在缓存空间和能量受限的机会网络中，MIEBR均衡了节点的能量消耗，降低了重要消息的传输延时，提高了消息投递成功率，并具有较低的平均消息延时和网络开销。下一步的工作是设计安全机制和信用机制，保证节点用户社会上下文隐私安全和促进节点用户之间的合作。