平衡损失函数下具有时间效应和通胀因子的信度估计
张 强,陈 萍
(南京理工大学 理学院,南京210094)
0 引言
信度理论是一种基于历史索赔数据来计算未来保费的经验厘定方法,它广泛应用于汽车保险、工伤赔偿金及赔款准备金。当代的信度理论归功于Bühlmann[1],他首次在现代统计决策理论框架下建立了无分布限制的信度理论,这为信度理论的发展奠定了统计基础,关于信度理论的详细介绍,可见Bü hlmann和Gisler[2]。
大批学者对信度理论进行了研究,并建立了各种各样的信度模型,这些信度模型极大地依赖于风险间的独立性及时间分量上的条件独立性。事实上,在保险实务中,这种假设有时候是不成立的,风险间存在较强的相依性。近年来,关于风险间的相依性的研究引起了越来越多的精算研究者的重视。如,Yeo等[3]建立了风险具有随机共同效应的信度模型,得到了正态-正态分布下的信度公式。Wen等[4]推广了Yeo等[3],提出了共同效应相依的无分布信度模型。之后,Wen和Deng[5]研究了风险等相关结构的信度估计等。另一方面,多数学者对时间分量上相依的信度模型进行了研究,具体包括郑丹等[6]、Purcaru和Denuit[7,8]、Frees和Wang[9]。最近,Huang和Wu[10]研究了风险相依和时间效应的信度模型。
然而,以上所提到的信度模型总是采用平方损失来刻画保费与风险的适合程度。有研究发现由于正(负)误差引起的损失不同,采用对称损失函数得到的估计不准确。因而,非对称损失函数得到了广泛的应用,其中,平衡损失函数是一类常见的非对称损失函数。Zellner[11]给出了如下形式的平衡损失函数:
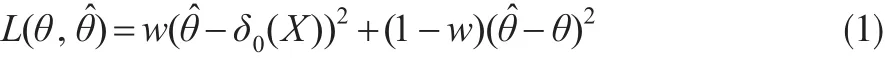
其中δ0(X)为目标估计,w∈[0,1]为已知的权重。
本文在平衡损失数下,研究了具有时间等相依及通胀因子的信度模型,分别得到了非齐次和齐次信度估计,并给出了结构参数的无偏估计。
1 模型假设与准备知识
假设某保单组合具有K种保单,每种保单含有ni年历史索赔数据。记第i种保单前ni年历史数据为 Xi=(Xi1,…Xin)′,则所有的历史数据为 {Xij,i=1,2,…,K,j=1,2,…,ni}。类似于经典信度模型的假设,认为第i种保单未来索赔Xi,ni+1是由所有历史索赔数据决定的。本文研究满足如下假设的信度估计。
假设1 :给定 Θi,随机序列 Xij,j=1,2,…,ni具有条件期望 E(Xij|Θi)=rjμ(Θi),条件方差 Var(Xij|Θi)=r2jσ2(Θi)以及条件协方差 Cov(Xis,Xit|Θi)=rsrtρ(Θi),s≠t,i=1,2,…,k,其中r是通货膨胀因子。
假设2:风险参数 Θ1,Θ2,…,ΘK是相互独立的,具有相同的结构分布函数 π(θ),且有 E(μ(Θi))=μ ,E(σ2(Θi))=σ2,E(ρ(Θi))= ρ ,Var(μ(Θi))=τ2。本文的目的是基于所有的历史数据,来预测未来时期的索赔 Xi,n+1的信度保费,此时需解决如下最优化问题:为了估计 Xi,ni+1,定义下面两类样本的线性函数类,分别称为样本的非齐次和齐次函数类。所以 Xi,ni+1的非齐次估计̂i,n+1与齐次信度估计分别定义为在各自线性函数类使得期望损失(2)最小。
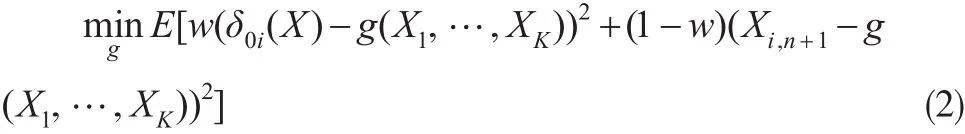
为统计δ0(X),引入记号:
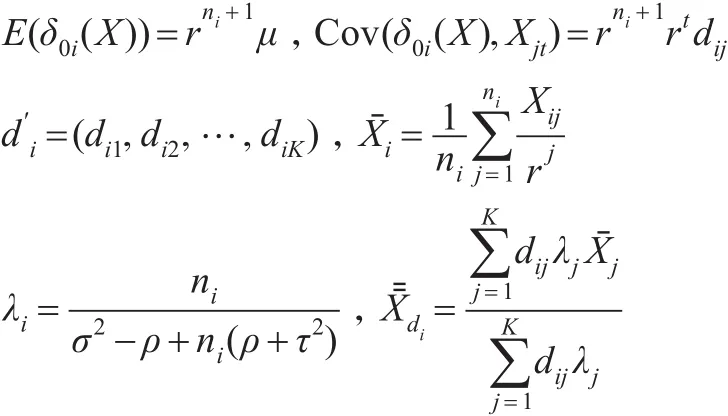
为方便求解非齐次与齐次信度估计,下面给出一些准备型的引理。
引理1:随机变量Y在线性空间L(X,1)和Le(X)上的正交投影分别称为Y的非齐次和齐次信度估计,即有:
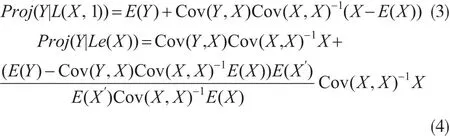
其中Cov(X,Y)是Y与X的协方差矩阵,证明可见[2,4]。引理2:在假设1和假设2下,有以下结论成立
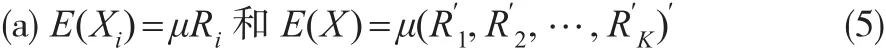
其中 Ri=(r,r2,…rnj)'

其中
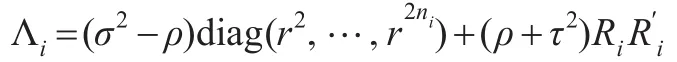
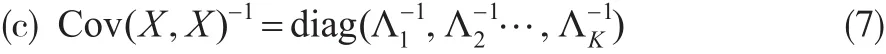
其中
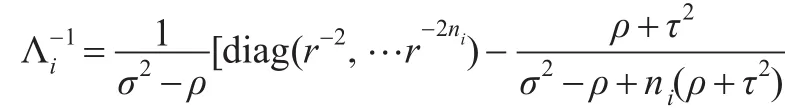
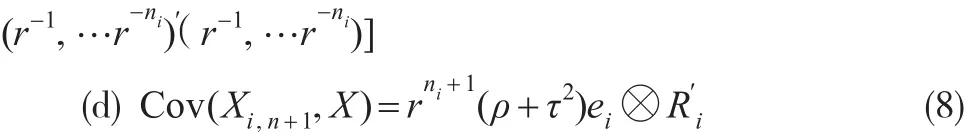
证明:(a)记 Θ=(Θ1,Θ2,…,ΘK),由重期望公式,可得:E(Xi)=E(E(Xi|Θi))=E(μ(Θi)Ri)= μRi
从而:

(b)由协方差的双重期望定理,有:从而,有:
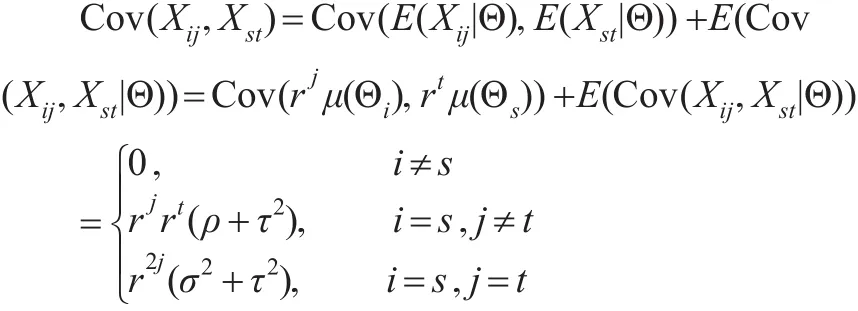

所以有式(6)成立。

可得:
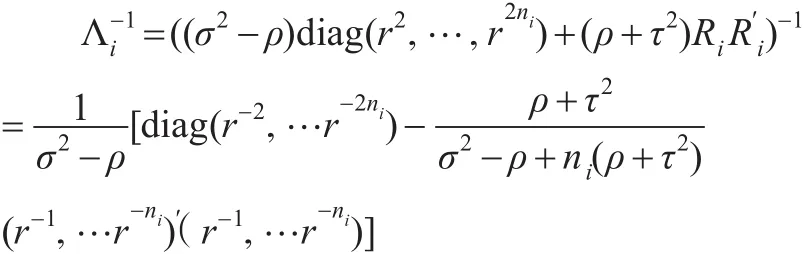
进一步,可得式(7)。
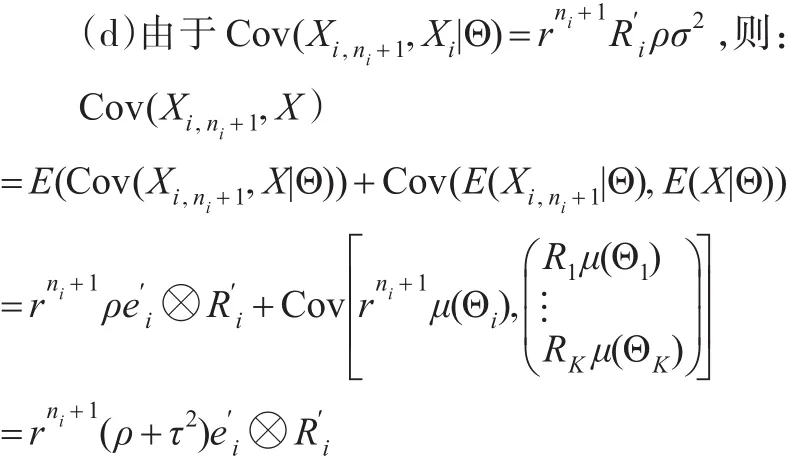
下面将利用正交投影方法求解问题(2),获取未来索赔Xi,ni+1的非齐次和齐次信度估计。
2 信度估计
定理1:在假设1和假设2下,通过求解最小化问题(2),可得 Xi,ni+1的非齐次信度估计为:

证明:令Yi=(1-I)δ0i(X)+IXi,n+1,其中 I为独立于其他变量的0-1随机变量,且满足P(I=0)=1-P(I=1)=w。则最小化问题(2)等价于:
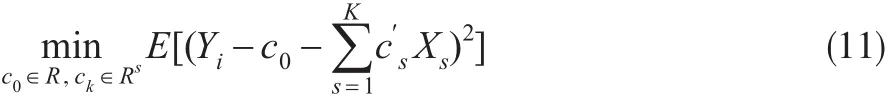
由引理2,知 Xi,ni+1的信度估计为:
从Yi的定义有期望E(Yi)为:

事实上,E(X|I)=E(X),从而:

所以协方差矩阵Cov(Yi,X)为:
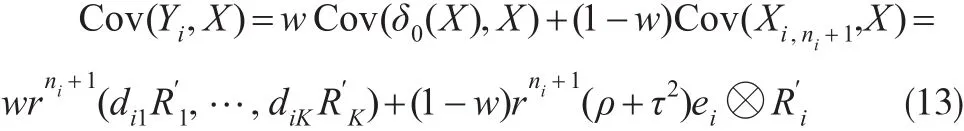
利用引理1,计算可得:
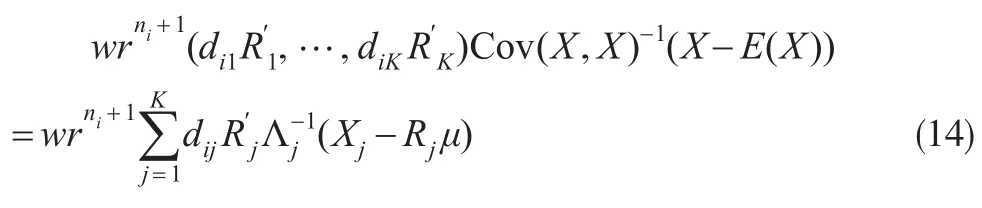
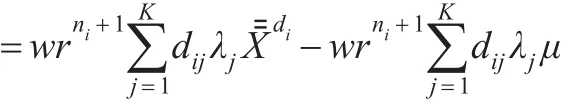
而

故 Xi,ni+1的信度估计为:
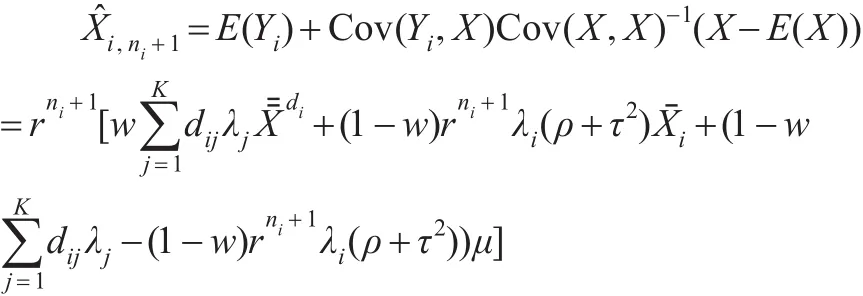
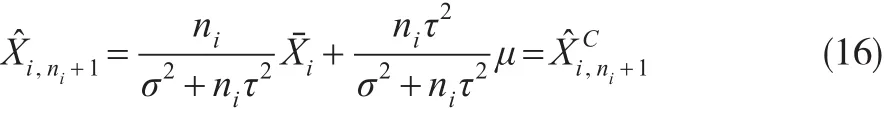
此结果为经典的B ü hlmann信度估计,具体可见B ü hlmann和Gisler[2],本文的模型是其的一个推广。
注 2 :若取 δ0i(X)=rni+1,则有 E(δ0i(X))=rni+1μ ,通过计算可得:当i≠j时,dij=0,当i=j时+(ρ +τ2),则
从而可得信度估计:
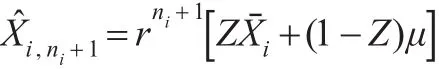
其中信度因子

当μ未知时,定理1不能直接应用,需将问题(2)的估计限定在样本的齐次函数类中,来计算Xi,ni+1的齐次信度估计,结果叙述为下面的定理。
定理2:在假设1和假设2下,未来索赔 Xi,ni+1的齐次信度估计为:
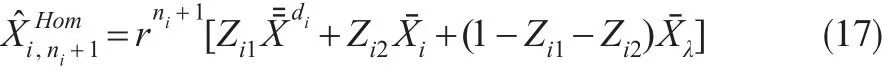

其中,而Zi1,Zi2和定理1一致。
证明:由正交投影的平滑性:
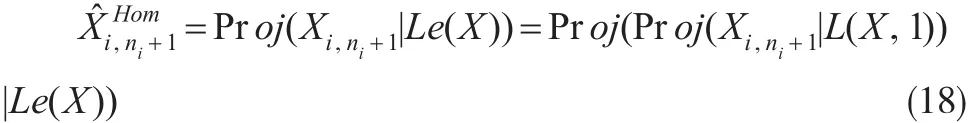
注意到

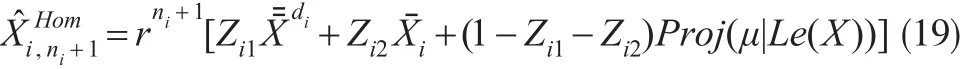
进而,令Y=μ,因为Cov(μ,X)=0,所以:
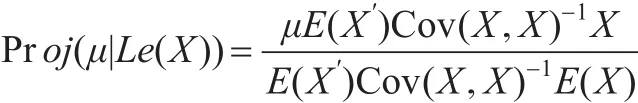
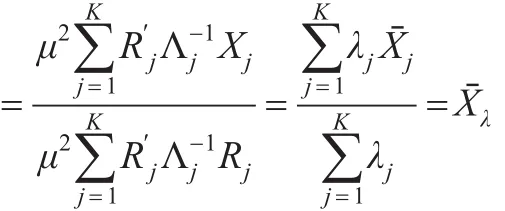
从而式(17)成立。
在定理1和定理2中,本文给出了Xi,ni+1的非齐次和齐次信度估计,然而包含了未知的结构参数μ,σ2,ρ和τ2。这需要利用历史索赔数据{Xij,i=1,2,…,K,j=1,2,…,ni}来估计。由定理2的证明,可知μ的一个无偏估计而 σ2,ρ 和 τ2的无偏估计由以下性质给出。
性质1:结构参数σ2的无偏估计为:
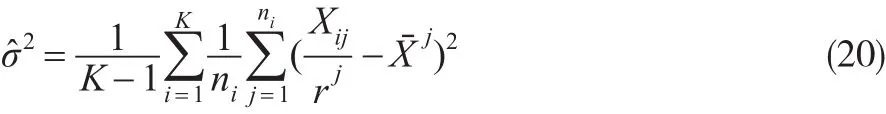

因此:
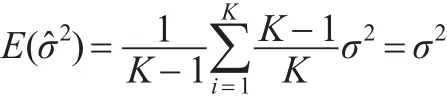
性质2:结构参数ρ的无偏估计为:
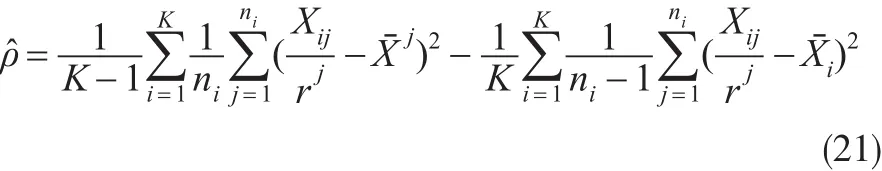
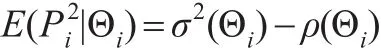
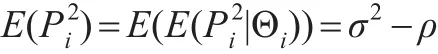
所以:
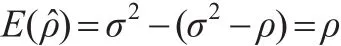
性质3:结构参数τ2的无偏估计为:

从而:
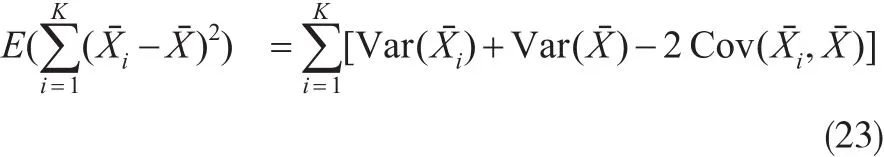
利用双重期望定理,有:

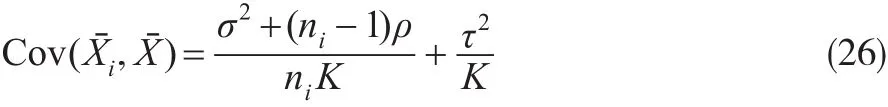
将式(24)至式(26)代入式(23),则:
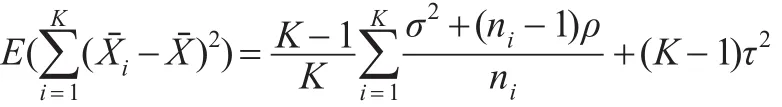
所以 E(τ̂2)= τ2。
3 数值模拟
下面将对定理1的结果进行数值模拟。为了说明问题,假定 n1=n2=…nK=n,K=5,并且随机向量 Xi~N(ΘiRi,Σ) 和 Θi~N(μ,τ2) ,i=1,…,K ,这 里 协 方 差 矩 阵
在模拟中,取 δ0i(X)=rni+1,r=1.05,μ=0.6 ,σ2=1.5,ρ=0.45和τ2=2.1。据以上的假设,产生伪随机数 Xij,j=1,…,n+1,i=1,2,…,5,其中{Xi,n+1,=1,2,…,5}为待估计的真实值,{Xij,j=1,2,…,n,i=1,2,…,5}为样本值。通过式(10)和式(16),分别得到了信度估计,得到不同权重 w 下不同 n 时̂i,n+1与与 Xi,n+1的均方误差 MSE 和 MSEC,重复执行10000次模拟,得到的结果如表1和表2所示。

表1 w=0.2时的模拟结果

表2 w=0.6时的模拟结果
4 结束语
本文在平衡损失函数下研究了具有时间效应及通胀因子的信度保费。利用正交投影方法,得到了未来保费的非齐次和齐次信度估计。同时,给出了信度因子中未知结构参数的无偏估计。这一结果推广了经典的信度模型,为非寿险保险公司厘定未来保费提供理论依据。

