一种改进的无迹Kalman滤波在SINS/GPS组合导航中的应用

陈国通，范圆圆，刘 琪

(河北科技大学信息科学与工程学院，石家庄 050018)

0 引言

随着航空航天技术的发展，对导航与定位系统的性能要求越来越高，单一的导航系统已经无法满足工程实践的需要，组合导航系统应运而生，并且得到了广泛应用[1]。应用最广泛的就是捷联惯导系统(strap-down inertial navigation system, SINS)与全球定位系统(global position system, GPS)的组合[2]。SINS是一种自主式导航系统，不需要外部信息就可以完成导航，在导航过程中也不会向外部辐射能量，具有很好的隐蔽性，但随着时间的推移会有误差的积累[3]。GPS可以全天时、全天候工作，且定位精度高，导航误差不会积累，但是易受干扰和建筑物遮挡[4]。这两个导航系统可以优势互补，能够提供非常完整的导航数据和精确的导航信息[5]。

1960年，R. E. Kalman提出了Kalman滤波算法[6]。但是它只适用于系统模型为线性，且过程噪声和量测噪声都是Gauss分布时的情况[7-8]。当系统模型为非线性，且过程噪声和量测噪声都是非Gauss分布时，该方法就不再适用[9-11]。此时就出现了无迹Kalman滤波(Unscented Kalman Filtering， UKF)。本文针对无迹Kalman滤波导致滤波性能急剧下降和发散的问题，提出了基于抗差因子的无迹Kalman滤波。一方面通过扩维，增加了系统的输入信息，减小了噪声对系统的影响；另一方面可以减小异常观测量对状态估计值的影响。

1 SINS/GPS组合导航数学模型

SINS选取东北天地理坐标系n作为导航坐标系，采用20维的状态参数来建立系统状态方程。SINS/GPS的状态量为

(1)

SINS/GPS组合系统的状态方程为

(2)

式中，X(t)为20维的系统状态量，f(·)为状态量的非线性函数，W(t)为20维的系统过程噪声。

SINS/GPS组合系统的量测部分的观测值，需要选取SINS与GPS的位置、速度之差。因此，系统的量测方程为

Z(t)=h(X(t))+V(t)

(3)

式中，h(t)表示伪距、伪距率的非线性观测方程，V(t)表示伪距、伪距率的白噪声。

2 无迹Kalman滤波算法

2.1 无迹变换

无迹变换的具体步骤如下：

(1)计算2n+1个采样点和权值

(4)

(5)

(2)计算非线性映射得到的Sigma点

利用非线性映射h(·)，对采样得到的每个Sigma点做非线性变换，得到点集yi

yi=hxii=0,1,…,2n

(6)

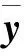
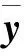
(7)

2.2 无迹Kalman滤波算法实现

无迹Kalman滤波是一种近似线性的最小方差估计方法，它的依据就是无迹变换，以经典Kalman滤波算法为框架，采用确定性采样来完成整个过程。UKF不需要对系统的状态和量测方程提出任何要求，就可以计算出最佳增益阵，因而既适用于线性系统模型，也适用于非线性系统模型。其具体实现步骤如下：

(1)初始化

初始状态和初始方差如式(8)和式(9)所示

(8)

(9)

将式(8)和式(9)扩维得到

(10)

(11)

(2)Sigma点采样

(12)

(13)

均值和协方差的权值如式(14)和式(15)所示

(14)

(15)

(3)时间更新

首先，根据状态方程传递采样点

(16)

接着，根据预测采样点、均值和协方差的权值计算预测均值和协方差

(17)

(18)

预测测量值和协方差

(19)

最后，得到预测测量值和协方差

(20)

(21)

(22)

(4)计算UKF增益，更新状态向量和方差

(23)

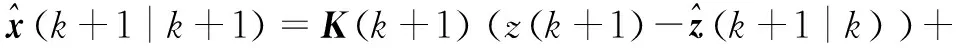
(24)

k+1|k

(25)

3 改进的无迹Kalman滤波

传统的无迹Kalman滤波根据估计量测方程和量测量的协方差矩阵来确定最佳增益，但在导航过程中会因为外界因素的干扰，无法得到准确的量测信息，致使增益有所偏差，导致最后的滤波精度降低。基于此，本文提出了一种改进的无迹Kalman滤波方法。首先对新息(即预测残差向量)的信息进行观察分析，判断是否有异常的观测量，并对异常的观测量进行修正，此修正过程就是通过引入抗差因子来完成的。

设定新息向量νk

(26)

式中，diag(·)表示求取方阵的对角线元素为列向量，m表示m维观测向量，σ为一参数，根据反查标准正态分布表，确定其取值范围应为2.3～4.3。

当k时刻m维的γm(k)全都小于0，则证明新息向量正常；若存在某一值使得γm(k)大于0，则k时刻的某行量测新息存在异常,此时需要引入抗差因子。本文采用的抗差因子是根据IGGⅡ型权函数生成的。

基于预测残差νk构建预测残差判别统计量Δνk，表示为

(27)

IGGⅡ型权函数为

(28)

式(28)中，k0、k1均为常数[11]，取值范围分别为1.0～1.5、2.5～8.0。根据式(28)生成的抗差因子函数为

(29)

将式(29)带入式(26)得到

(30)

此时可以根据抗差因子函数来调整新息向量观测到的异常值，使式(30)的结果不大于0，即γm(k)得到的结果全都不大于0。通过抗差因子调整后，得到的Sigma点集为

(31)

根据第2节无迹Kalman滤波过程，得到改进的无迹Kalman状态与方差估计为

(32)

(33)

4 仿真与结果分析

为了证明改进算法的有效性，本文设计了基于matlab的仿真实验，并将此算法应用到SINS/GPS组合导航系统中进行仿真。仿真实验中的各初始参数设定如表1所示。设运载体初始所在位置为东经114.26°，北纬38.03°，地球的自转角速为ωie=7.292×10-5rad/s，初始速度为v=100m/s，仿真时间为1000s。

图1和图2分别为UKF估计、改进的UKF估计和真实状态比较，通过分析其状态值和绝对偏差值，可以看出改进的UKF更接近真实值。

表1 仿真参数

图1 UKF/改进的UKF状态值估计Fig.1 UKF/ improved UKF state value estimation

图2 UKF/改进的UKF绝对偏差值估计Fig.2 UKF/improved UKF absolute bias value estimation

图3～图5为EKF、UKF和改进的UKF在水平和垂直方向上的误差曲线。分析比较可以看出，改进的UKF误差曲线更加平滑，更加收敛。

图3 EKF水平/垂直方向误差Fig.3 EKF horizontal and vertical errors

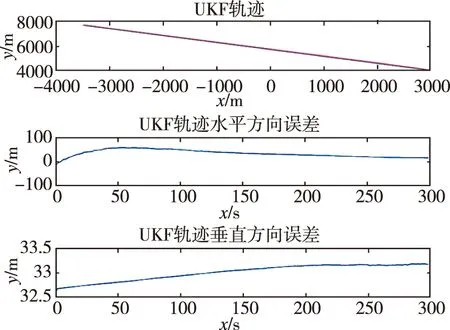
图4 UKF水平/垂直方向误差Fig.4 UKF horizontal and vertical error

图5 改进的UKF水平/垂直方向误差Fig.5 Improved UKF horizontal and vertical error

本文采用的是东北天坐标系，所以对东向速度误差和北向速度误差进行分析，如图6和图7所示。可以看出3种算法得到的速度误差的滤波精度逐渐提高。EFK算法得到的速度误差在(-0.5m/s，0.5m/s)以内，UKF算法得到的速度误差在(-0.3m/s，0.3m/s)以内，改进的UKF算法得到的速度误差在(-0.1m/s，0.1m/s)以内。

图6 东向速度误差曲线Fig.6 Eastward velocity error curve

图7 北向速度误差曲线Fig.7 North direction velocity error curve

5 结论

传统的无迹Kalman滤波在非线性系统中能够很好地提高鲁棒特性和收敛速度，但是在观测过程中容易出现量测新息不规则的情况。因此，本文提出了一种改进的无迹Kalman滤波方法，一方面根据新息向量的概率特性，能够及时发现异常信息；另一方面通过引入抗差因子来对异常信息进行修正。通过仿真实验证明，本文提出的改进算法能够提高组合导航系统的滤波解算精度，对SINS/GPS组合导航的研究具有一定的参考价值。