星载抛物面天线视在相位中心确定方法及应用

沈迎咏，高晶波，王 聪

(哈尔滨工业大学航天学院，哈尔滨 150001)

0 引言

随着通信、雷达、人造卫星的发展，天线在国防领域的应用越来越广泛，由于抛物面天线具有发射功率大、副瓣较低、结构简单易加工、相关技术较成熟等优点[1]，常常被选择作为发射天线或阵列单元。例如SAR卫星[2-3]采用大口径可展开抛物面天线，馈源处安置喇叭天线，它的主要任务是通过微波成像的方式获取地面目标的图像情报信息，结合多种成像工作模式，实现对地面目标的详查和普查。为了适应微波载荷提出的空间高分辨率、定位高精度、探测高灵敏度的参数指标，卫星天线需具备更高的指向精度[4]和稳定度[5]，而这些均与天线的相位中心密切相关。

相位中心在卫星天线研究中占有重要地位。为了实现反射面天线高增益和低副瓣电平的目标，必须把馈源喇叭天线相位中心[6-10]放置在反射器抛物面的焦点处。由于喇叭天线的辐射场不是理想的球面波，因此不存在严格的相位中心，但实际应用中仍需要确定一个近似的相位中心，并使其与抛物面焦点重合，以便得到最大的天线增益，该点便称为“视在相位中心”[11-13]。在实际应用中将对视在相位中心进行测量，来替代物理意义上的相位中心。确定喇叭天线的视在相位中心有两种方法：一种是实验方法[14]，该方法将喇叭天线放置在抛物面天线的焦点附近做轴向移动，确定抛物面天线的增益最大(或者主瓣宽度最窄)时的喇叭天线的位置，从而确定视在相位中心。实验方法虽然简单，但需要进行重复的实验，工作量大，效率低。另一种是从理论近似分析求得[3]，该分析需要计算抛物面天线主波束一定角度范围内的多个测点的远场相位方向图的相位波动值，当某点方向图的相位波动最小时，这个点就称为天线的视在相位中心，此时抛物面天线视在相位中心的计算公式很复杂，不能直接应用于工程实际中。因此，本文结合具体的实际问题，建立卫星有限元模型，基于多体系统动力学在轨仿真分析，利用抛物面天线的工作原理以及视在相位中心的定义，拟合抛物面天线在机动过程中的视在相位中心位置，并利用最小二乘法分析视在相位中心坐标偏移量。对比分析有阻尼器和无阻尼器两种连接方式对天线视在相位中心偏移量的影响，为抛物面天线指向精度的研究提供参考。

1 抛物面天线工作原理与视在相位中心

抛物面天线是由抛物面反射器和位于其焦点处的馈源组成的面状天线，馈源处通常安置喇叭天线。如图1所示，抛物面天线有以下两个重要的性质[15]：1)由焦点F发出的射线经反射器抛物面反射后，所有反射线都与抛物面轴线平行；反之，当平行射线沿抛物面轴线入射到抛物面上时，被抛物面反射后，其反射线均汇聚于焦点处。2)由焦点发出并经抛物面反射的各条射线，到达垂直于抛物面轴线任一平面时的波程相等，因此，垂直于轴线的平面为等相位面。这两个性质的证明如下：

图1 反射器在xz平面内的横截面Fig.1 Cross section of the reflector in the xz plane

O点为反射器抛物面的顶点，F为焦点，焦距为f，M为反射器表面上一点，M点与焦点F的距离为rf，该抛物线用极坐标rf,θf可表示为

(1)

(2)

归一化得

(3)

则入射角αf与反射角为αi可以求得

(4)

(5)

因此可以得出

(6)

(7)

性质1)由此可以证明。

下面证明性质2)，从焦点到口径面的总长度为

FM+MN=rf+rfcosθf=rf1+cosθf=2f

(8)

因为总长度是恒定的，从焦点处的馈源到达口径平面的波相位也恒定。

以上两个重要的性质是抛物面天线的工作基础。基于以上性质，抛物面天线用作发射天线时，位于焦点F处的弱方向性馈源向抛物面辐射球面波，经抛物面反射的电磁波变成沿轴线传输的截面约为抛物面口径的平面电磁波(相位相同)，使反射器口面场形成均匀分布，均匀口面场将产生方向性辐射场，反之，如果把抛物面天线用作接收天线，入射波又是平行于抛物面轴线的平行波形式，经反射器反射后则会把平面波转换成球面波传送到位于焦点位置的馈源(相位中心)，形成聚集接收，增加其接收信号的强度。因此，从物理现象上电磁波相当于从一点发出或者被同一点接收，定义此点即为抛物面天线视在相位中心。

2 整星多体系统动力学仿真

整星多体模型包括星本体、天线系统、左右对称的帆板等。本文重点研究天线视在相位中心，因此将星本体视为刚体，馈源简化为圆形平面薄板，如图2所示。整星在方位向(X轴)上定轴转动，范围为0°～90°，这个过程中保持动中成像，有指向精度与稳定度要求，然后成像结束，恢复初始位置，调姿曲线如图3所示。本文仿真环境是：整星受到距离向即x轴正方向的飞轮干扰力、飞轮干扰力矩以及太阳电池阵驱动机构(SADA)扰动。飞轮干扰力及干扰力矩采用四阶谐波叠加

(9)

其中，m(t)为扰动力或扰动力矩；n为模型中含有的谐波数；Ω为转速；hi为第i次谐波数；Ci为与mt相应的第i次谐波的幅值，单位为N/Hz2或N·m/Hz2；αi为随机相位角，假设均匀分布在0,2π。本文仿真分析中，飞轮转速为6000r/s，飞轮谐波系数如表1所示，飞轮干扰力如图4所示，飞轮干扰力矩如图5所示。考虑SADA扰动时，由于轴向干扰力矩为主要扰动因素，径向干扰力为次要扰动因素，本次仿真忽略SADA干扰力的影响，只建立SADA扰动力矩的模型，干扰力矩的均值为2N·m，方差为0.3(N·m)2，如图6所示。

图2 整星仿真模型Fig.2 Whole star simulation model

图3 整星调姿曲线Fig.3 Whole star attitude curve

图4 飞轮干扰力曲线Fig.4 Flywheel interference force curve

图5 飞轮干扰力矩曲线Fig.5 Flywheel interference torque curve

图6 SADA扰动力矩曲线Fig.6 SADA interference torque curve

采用不同的连接方式进行仿真分析，各仿真工况如表2所示，分析不同工况下视在相位中心的位置。

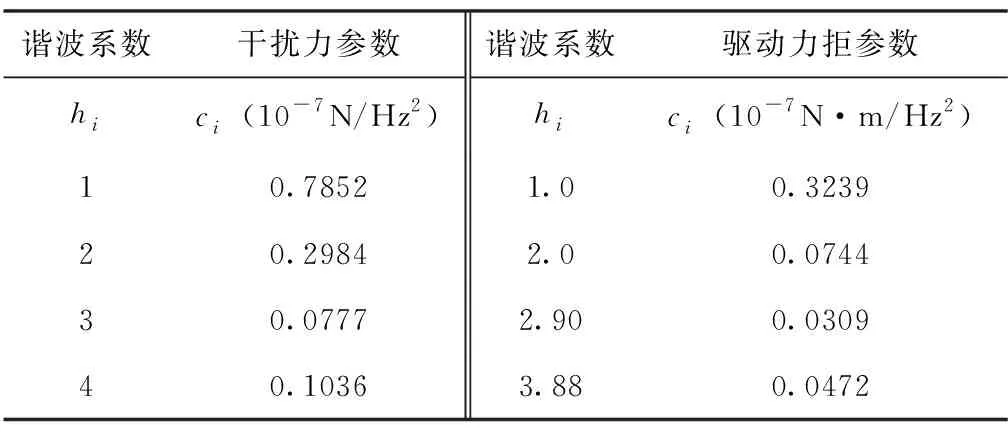
表1 飞轮谐波系数

表2 多体动力学仿真工况

3 天线视在相位中心的计算

采集不同仿真工况下反射器抛物面标志点坐标，利用最小二乘法拟合抛物面方程。仿真过程中，坐标原点放置在天线底部中心，采集xz面与yz面天线内反射表面标志点坐标，分别拟合计算焦点(x0，z0)和(y90，z90)，得到视在相位中心(x0，y90，(z0+z90)/2)。下面以天线不动时为例求解天线视在相位中心。

初始时刻xz面与yz面天线内反射面标志点坐标如表3、表4所示，利用最小二乘法分别拟合标志点如图7中(a)、(b)所示，可得xz面拟合曲线为

表3 xz面内标志点坐标

表4 yz面内标志点坐标

z=8.3443×10-5x2-5.7066×10-8x+1.5001

(10)

得其焦点x0,z0为(3.4149×10-2，3011.0739)，yz面拟合曲线为

z=1.8343×10-5y2+4.2329×10-6y+1.5007

(11)

得其焦点y90,z90为(-0.0253，3011.0582)，即可得到视在相位中心(x0，y90，(z0+z90)/2)为(3.4149×10-2，-0.0253，3011.0661)。

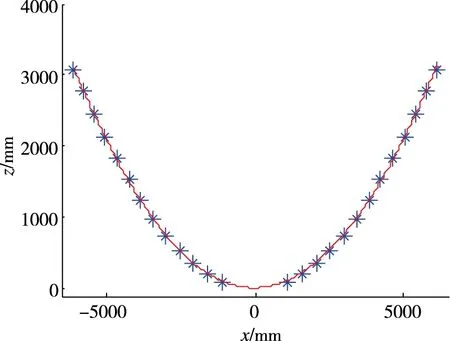
(a) xz面内拟合面

(b) yz面内拟合面图7 抛物面拟合图Fig.7 Parabolic fitting

依照此方法可以拟合得到天线机动过程中的相位中心，利用最小二乘法拟合可得视在相位中心坐标偏移量，从而可得天线机动过程中的视在相位中心坐标范围。进行仿真工况1时，天线与中心平台无阻尼器连接，拟合可得视在相位中心坐标偏移量如图8所示。从图8中可以看出，视在相位中心在天线机动过程中受到飞轮干扰以及SADA扰动的影响，x坐标的偏移量范围Δx∈-0.2169,0.2358，y坐标的偏移量范围Δy∈-0.0184,0.0249，z坐标的偏移量范围Δz∈-0.1569,0.2093，由于整星在方位向(x轴)定轴转动，因此y坐标偏移量最小。

图8 无阻尼器连接时天线视在相位中心偏移量Fig.8 The deflection of the antenna in the phase center when the damper isn’t connected

进行仿真工况2时，天线与中心平台有阻尼器连接，拟合可得视在相位中心坐标偏移量如图9所示。从图9中可以看出，视在相位中心在天线机动过程中受到飞轮干扰力、干扰力矩以及SADA扰动的影响，x坐标的偏移量范围Δx∈-0.0988,0.0953，y坐标的偏移量范围Δy∈-0.0160,0.0170，z坐标的偏移量范围Δz∈-0.0011,0.0010，由于阻尼器的作用，视在相位中心的坐标偏移量都减小，其中z坐标偏移量最小。

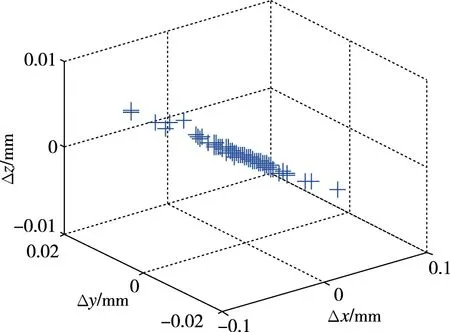
图9 有阻尼器连接时天线视在相位中心偏移量Fig.9 The deflection of the antenna in the phase center when the damper is connected

对比两种工况下的视在相位中心的变动范围，如表5所示，整星在方位向(X轴)上定轴转动，范围从0°～90°，受到距离向即x轴正方向的飞轮干扰力、干扰力矩以及SADA扰动，有阻尼器连接的天线视在相位中心的振动量明显小于无阻尼器连接的情况，阻尼器连接方式的天线视在相位中心最大偏移量Δz的变化量比无阻尼器连接的天线降低了两个数量级。

表5 视在相位中心偏移量对比

4 结论

本文针对星载抛物面天线成像过程中对波束的指向精度的要求，提出了天线视在相位中心的确定方法，并利用多体系统仿真方法研究了卫星机动过程中的视在相位中心范围及影响因素，得到以下结论：

1) 给出了抛物面天线视在相位中心的定义，并利用最小二乘法拟合得到了天线视在相位中心的位置。

2)天线视在相位中心的偏移量的分量受天线运动方向的影响，整星在方位向(X轴)上定轴转动，x坐标偏移量最大。

3)天线在机动过程中，无阻尼连接的天线视在相位中心的z偏移量在(-0.1569，0.2093)范围内，有阻尼器连接的天线视在相位中心的z偏移量在(-0.0010，0.0011)范围内，最大偏移量降低了两个数量级；无阻尼连接的天线视在相位中心x偏移量在(-0.2169,0.2358)范围内，有阻尼器连接的天线视在相位中心的x偏移量在(-0.0988,0.0953)范围内，最大偏移量降低一个数量级，阻尼器对天线视在相位中心x,z方向的震荡有明显的抑制。

以上不同工况的仿真结果表明，本文所提出的方法能够准确给出机动过程中抛物面天线视在相位中心，为抛物面天线指向精度和稳定度分析提供理论基础。