不同密度比球体入水空泡流体动力特性研究

李达钦，王国玉，张敏弟，黄 彪

(北京理工大学机械与车辆学院, 北京 100081)

0 引言

结构体入水运动涉及固、液、气的三相耦合作用，是一个具有强瞬态和非定常运动特性的过程，伴随着湍动、相变、可压缩、介质突变等大量复杂的流动现象[1-3]。入水现象普遍存在，并在自然科学、工业生产及仿生技术等领域有着广泛应用[4-8]。尤其是在航空航天领域，飞机的水上着落、飞船返回舱水上回收等正是利用入水空泡及自身结构的耦合作用实现航行和弹道稳定[9-12]，因此对入水空泡及其流体动力特性的研究具有很强的工程应用及科学研究意义。

近年来，国内外学者针对球体入水问题开展了大量研究。在实验方面，Aristoff等[13-14]对不同密度比的疏水性球体入水空泡发展特性进行了实验和理论研究，总结了空泡形态与韦伯数以及邦德数之间的关系，同时指出密度较小的球体有较大的速度衰减，空泡的夹断深度比与傅汝德数无关。Shepard等[15]针对不同密度比球体在不同入水冲击速度下的动力特性开展了研究，结果表明空泡夹断前球体所受总流体力会产生波动，尤其准静态空泡闭合瞬间受力波动最大。Truscott等[16-17]以球体为研究对象，针对入水溅射水冠和球体入水过程的非定常受力开展了实验研究，结果表明水冠的发展受大气压强影响显著，密度较小的亲水球体受到阻力最大。随计算机技术的发展，计算流体力学方法在处理入水问题方面得到了广泛应用。Iranmanesh等[18]、Mirzaii等[19]基于VOF(Volume of Fluid)方法和不可压缩流假设建立了一种运动体入水数值计算方法，应用该方法计算的不同密度球体入水空泡和轨迹均与实验拟合较好，并进一步将方法应用于圆柱入水计算，讨论了圆柱密度比、几何参数及入水冲击速度对入水轨迹的影响规律。Abraham[20]运用VOF多相流模型并耦合SST(Shear Stress Transport)湍流模型数值模拟了球体垂直入水初期阶段自由液面发展过程以及阻力特性，对比了不同入水速度、球体密度等参数，结果表明入水初期运动体阻力主要来源于入水物体与周围流域的动量转换。Ding等[21]通过数值模拟研究了球体及柱体垂直入过程产生的入水空泡，并实现了移动接触线的计算，结果表明接触线钉扎现象对随后入水空泡发展过程有显著影响。张伟伟[22]采用多物质ALE(Arbitrary Lagrangian-Eulerian)仿真方法，对球体入水时引发的水花、空泡及其所受冲击力等内容进行了系统的研究。通过与实验、理论数据对比，证明了多物质ALE 方法不仅可以再现结构入水的复杂过程， 还能较好地反映密度、冲击速度及表面亲水性等因素的影响。

目前国内外针对不同密度比航行体入水问题已有一些研究，但针对跨介质时的溅射水冠发展规律、入水空泡形态随球体密度比变化的详细分类以及水下流体动力特性的研究还需要进一步探索。本文基于实验与数值模拟相结合的方法，开展了不同密度比球体垂直入水研究,获得并分析了球体密度对垂直入水空泡形态、溅射水冠及水下流体动力特性的影响规律。

1 实验系统及方法介绍

基于高速摄像法建立的实验系统如图1所示。系统分为图像采集部、水箱以及发射部3部分。

图1 实验系统示意图Fig.1 Schematic of the experimental system

图像采集部由计算机、高速摄像机及光源组成。计算机负责储存和驱动Phantom V7.3高速摄像机对球体入水过程进行拍摄, 拍摄帧率为2000fps。同时实验设计了一套同步采集系统，在计算机端控制发射装置，可实现球体释放落水与摄像机采集的同步。实验中采用一组4×500W 的点阵光源通过柔光屏散射后照射水域, 并将两盏1000W 镝灯布置在水槽的左右两侧作为补充光源来达到良好的照明效果。实验水箱的尺寸为0.8m×0.8m×1m，四面及底面均为10mm厚的有机玻璃，底层铺有厚度为10mm的橡胶垫，以防球体与水箱底部撞击损伤底部玻璃。发射部由水箱外释放及支撑装置组成。为保证实验的可重复性和降低初始扰动，支撑装置采用可调节高度的型材支架，可实现球体从不同固定高度自由释放。释放装置固定在支架的水平支杆上并位于水箱中心正上方垂直于水面，装置采用内径27mm、高50mm的圆柱导轨，导轨内部设置有电磁铁控制的卡头，断电时卡头承接住球体，通电时卡头收回，球体便沿垂直方向自由下落。

实验采用5种不同材料的球体，密度比分别为m*=ρs/ρ=7.86、2.54、1.14 、0.94和 0.53(对应轴承钢、玻璃、两种不同类型树脂橡胶、轻质木材)，其中ρs为球体密度，ρ=998.2kg/m3为水的密度。实验球体直径D0均为25mm, 表面都涂有SY-Super coat-SHFC3150疏水性涂层，表面接触角θ均为150±0.5°，涂层所增加的球体厚度和质量可以忽略不计，除球体密度外实验球体其他参数相同，具体实验参数如表1所示。

2 数值计算方法介绍

2.1 控制方程

本文基于均相流模型，假定气液两相为均相流动，且相间无速度滑移，采用有限体积法求解Navier-Stokes方程[23]。低傅汝德数入水过程中无空化现象发生，考虑空泡闭合时内部高压可能会引起压缩效应，因此将空气相选为理想气体。控制方程包括连续性方程、动量方程及能量方程。分别为

(1)

(2)

(3)

式中，下标i和j分别代表坐标方向，ρm为混合介质密度，u为来流速度，p为流场压力，μm′为混合介质的动力黏性系数，μt为湍流黏性系数，κeff为有效传热系数，T为流体温度。根据均质平衡流模型假设，混合介质密度ρm和湍流黏性系数μm分别定义为

ρm=ρlαl+ρgαg

(4)

μm=μlαl+μgαg

(5)

本文采用VOF方法对水汽两相界面进行捕捉[23]；采用CSF(Continuum Surface Force)模型考虑接触角影响[24]；湍流模型选择SSTk-ω模型，该模型对强剪切流的计算上具有更高的精度和可靠性。

2.2 网格及边界条件

本文选取二维轴对称模型模拟不同密度小球垂直入水过程。图2展示了计算流域、网格及边界条件，其中球体直径D0=25mm与实验参数一致。在自由界面建立坐标系如图2所示，原点位于水面处，z轴正方向与重力加速度g方向相反。流域内采用全结构化网格，对于球体周围以及流经路径着重加密，确保y+=yuτ/vl≈1，流域内网格节点数约为25万。计算时间步长选定为Δt=1.00×10-7s，平均库朗数CFL=U∞Δt/Δx≈0.01。对球体垂直入水计算应用的动网格技术为动态铺层方式。利用6DOF求解器获得球体位置参数，并实现网格和数据实时更新，同时监测球体受力以及速度，为流体动力特性分析提供数据基础。

图2 网格及边界条件示意图Fig.2 Mesh for the whole domain and boundary conditions

2.3 数值方法验证

为了研究不同球体密度比对入水空泡、溅射水冠以及动力特性的影响，本文开展了不同密度比球体垂直入水实验和数值模拟计算。针对密度比m*=7.86，入水冲击速度U0=5.40m/s(Fr=U0/(gD0)0.5=10.9)的实验工况开展数值方法验证研究。图3展示了数值计算球体无量纲入水深度Z/D0随时间变化结果与实验结果的对比，以球体底部刚接触到水面的时刻为t=0ms时刻，用球心坐标表征球体位置。可以观察到总体上数值结果与实验结果吻合较好，尤其在40ms之前，数值结果与实验结果几乎一致，随着时间发展，数值结果略低于实验结果，平均误差在5%以内。图3中同样展示了典型时刻数值与实验入水空泡形态的对比，可观察到相同入水时刻空泡径向与轴向尺度均与实验结果拟合较好。由此可知，本文建立的数值模拟方法能够有效预测不同密度比球体垂直入水轨迹及空泡形态，证明了本文建立的数值模拟方法的准确性与可行性。

图3 数值计算入水轨迹与实验结果对比Fig.3 Comparison of sphere depth vs. time for the impact sequences of numerical results and experimental results

3 结果与讨论

3.1 不同密度比球体入水空泡及溅射水冠的发展规律

基于以上确立的数值计算方法，并结合实验结果，开展溅射水冠及入水空泡研究。通过处理实验拍摄的相邻入水图像，可以获得入水冲击速度。球体释放高度H对应入水冲击速度U0的范围为(0.7～7.0±0.1)m/s。所有实验工况均展示于图6，并选取3个典型密度比球体(m*=7.86、1.14和0.53)在4种入水冲击速度U0=0.7m/s、2.18m/s、5.40m/s和6.25m/s(Fr=1.4、4.4、10.9和12.6)工况下的入水空泡及溅射水冠进行对比，如图4所示。根据Duez理论[7]可知，表面接触角θ=150°的条件下形成入水空泡的临界速度U*=0.26m/s。理论预测结果与实验现象相符，实验设计速度均大于临界值并产生入水空泡。

(a)Fr=1.4, t= 55.0ms

(b)Fr=4.4, t= 63.0ms

(c)Fr=10.9, t= 59.5ms

(d)Fr=12.6, t= 57.5ms图4 不同密度比球体入水形态对比Fig.4 Comparison of cavity shape for water entry of spheres with different density ratio

图4的每组对比中，各球体入水图像所取的入水时刻相同。在入水空泡方面，总体上看密度越大的球体在相同入水速度下获得更大的动能，所以相同时刻会获得更大的入水深度。当Fr=1.4时，密度比小于1的轻质球(m*=0.53)会迅速上漂，其他两种密度球体随着下落，三相接触点迅速上移至球顶端，连接水面与球体的空泡逐渐形成半月牙状，此时重力和表面张力的平衡作用占主导地位，这种空泡形态称为准静态入水空泡。随着Fr增至4.4，轻质球(m*=0.53)依然处于准静态空泡阶段，而其他两种密度球体随着入水深度增加，入水空泡不断拉长，入水空泡逐渐向中心轴线收缩，到后期完整的入水空泡发生夹断形成上下两部分空泡，此刻的空泡状态称之为深闭合空泡，并且伴随出现向上向下的两股液态射流(图5(a))。当Fr继续从10.9增大到12.6时，密度最大的轴承钢球入水空泡尾部脱离自由液面，并且在自由液面处发生了闭合，此刻的空泡状态称之为面闭合空泡。闭合后脱离水面的空泡随着球体下落继续拉长，但面闭合位置出的空泡壁面在水静压作用下失稳，并产生垂直向下的水射流，水射流进入并撞击空泡后使得原本光滑的空泡壁面出现斑纹和扰动。同时随着球体入水深度增加，入水空泡出现明显的收缩趋势，并产生深闭合(图5(b))。与此同时轻质球依然处于准静态空泡阶段，树脂球依然处于深闭合空泡阶段。说明各流形之间的临界速度随着球体密度的增加而减小。

(a)Fr=4.4 (b)Fr=10.9图5 入水空泡深闭合图像，m*=7.86Fig.5 The images for deep seal, m*=7.86

在本实验的设计速度区间，对比所有实验结果可得到入水空泡形态之间的临界傅汝德数与球体密度的关系图，如图6所示。进一步将空泡形态分为准静态入水空泡、深闭合优先入水空泡、水冠闭合优先的深闭合入水空泡以及面闭合空泡，分别对应图6中Ⅰ、Ⅱ、Ⅲ、Ⅳ区域中所表征的类型。观察到密度小于水的球体在实验速度范围内时只能产生准静态空泡并无夹断生成，而密度大于水的球体则经历更为复杂的空泡形态，随着密度的增加，各空泡形态之间的临界速度降低同时降低速率减缓。由此可以推测，当球体密度持续加大，各空泡形态的临界速度会趋于稳定值。

图6 入水空泡形态的临界傅汝德数与球体密度比的关系Fig.6 Critical Froude number for cavity shape versus density ratio

针对水下空泡的深闭合与面闭合现象进行进一步分析，以Fr=10.9的钢球入水工况为例，图7(a)展示了空泡面闭合、空泡收缩以及空泡深闭合时的流场结构，图7(b)展示了对应的各个时刻沿轴线相对压力分布，参考压强为101325Pa。可以观察到，由于射流及水静压等因素的耦合作用，入水空泡内部出现大量多尺度漩涡结构，泡内出现高速气流和低压区，更进一步加剧了空泡的收缩。此外，空泡面闭合和夹断后会在闭合位置产生局部闭合高压，压力值远大于对应位置水静压，高压与射流促进了空泡的溃灭。

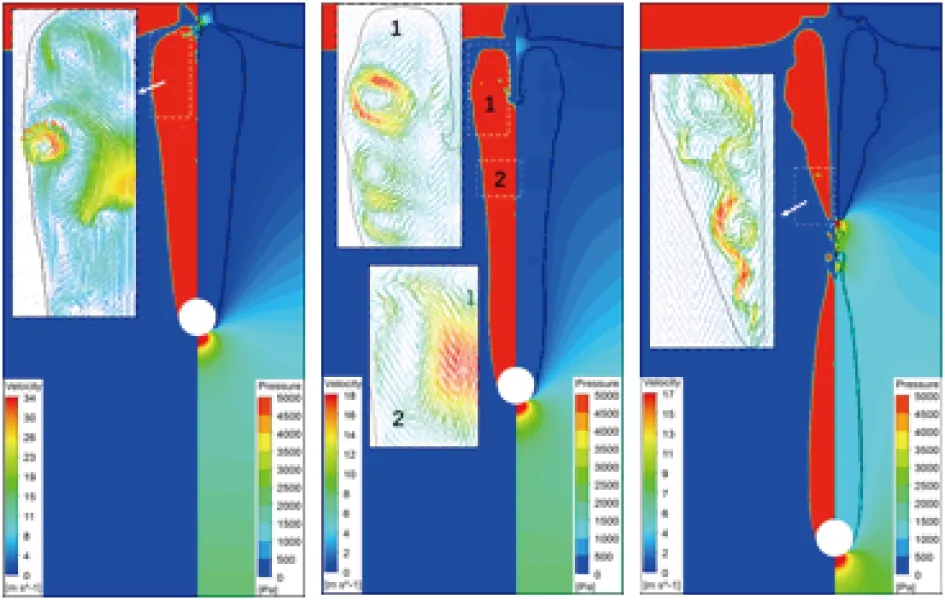
t=39.8ms t=50.3ms t=75.0ms(a)钢球入水流场结构云图，Fr=10.9

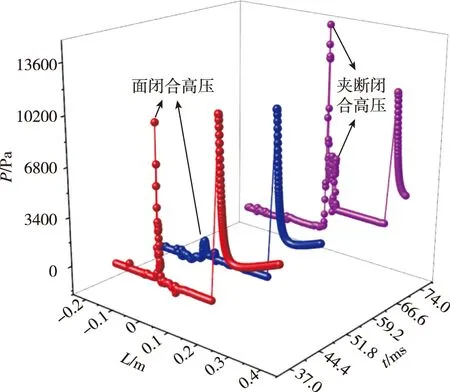
(b)沿轴线压力分布图，Fr=10.9图7 球体入水流场结构及压力分布Fig.7 The flow structures and preesure distribution for the impact of sphere

在溅射水冠方面，从图5实验结果中观察到入水傅汝德数较低(图4(a))时，各球体均未产生溅射水冠。当入水冲击速度还不足够大时(图4(b))，并不会发生水冠闭合现象,而是一边向中心收缩一边下落至水面，因此在空泡夹断前整个过程入水空泡始终与大气连通，这种空泡形态称为深闭合优先入水空泡。随着傅汝德数增加，水冠轴向径向增长迅速，在液面上方会发生碰撞闭合形成封闭圆顶(图4(c)和(d))，这种水冠闭合现象称之为早期表面闭合[16]，对应的入水空泡形态包括水冠闭合优先的深闭合入水空泡以及面闭合空泡两种。早期表面闭合伴随形成上下两股水射流，此时空泡内气体不再与外界大气压相连，向下的液体射流进入并撞击空泡壁面，造成原本一直光滑的空泡壁面发生扰动，会进一步加剧空泡壁面的不稳定。以钢球5.40m/s(Fr=10.9)入水工况为例，图8展示了其产生的溅射水冠发展过程，经历了初始溅射阶段、水冠成型与生长阶段以及水冠闭合与溃灭阶段。图9展示了对应的过程中几个典型时刻的数值计算结果，主要关注跨水界面区域的速度矢量和压强分布。可以观察到，当球体以较高速度冲击自由液面时，会与液面进行强烈的动量交换，进而形成飞溅，飞溅形成的水膜与球体发生分离，继续向四周扩散形成水冠。随着球体入水深度增加远离自由液面，球体对水冠向上生长影响逐渐减小，空气不断高速流入空泡并在水冠内部形成涡团结构，同时产生低压区。水冠在内外压差的作用下向中心轴线收缩，最终形成水冠闭合。

图8 球体入水水冠形态，m*=7.86，Fr=10.9Fig.8 The evolution of splash formation created by the impact of the steel sphere at m*=7.86, Fr=10.9

入水过程中会在球身某处形成固-液-气三相接触线，线上任意一点为三相接触点。图10定义了入水过程中三相接触点相对于球底的位置距离Hc。以前文中3种密度球体以Fr=10.9入水工况为例，图11展示了实验与数值计算中三相接触点垂直位置随着入水时间的变化。

图9 入水水冠发展典型时刻下的数值流场结构Fig.9 The numerical flow structure at some typical moments during the splash evolution

图10 三相接触点示意图Fig.10 Schematic illustration of the definition of triple line contact point

图11 三相接触点位置随时间变化图Fig.11 The history position of the triple line vs. time

接触点垂直位置用球体直径进行了无量纲处理，可以观察到数值结果与实验测量结果拟合较好。入水初期阶段各密度球体的接触点运动趋势近乎一致，均快速上升并随着球体入水深度增加最终稳定在约Hc/D0=0.35的位置，此时对应的是球体带空泡稳定下落阶段。这种稳定状态在约t=60ms时发生变化，轻质球体的接触点迅速上移并闭合在球顶，而其他密度球体的接触点仍然维持固定高度。此时对应轻质球体速度衰减剧烈不能给予附着空泡更多的动能克服水静压，接触点迅速上移至球顶部，附着的空泡形成准静态后迅速在球体顶部极点处闭合并脱离球体。同时其他密度大于水的球体所附着的空泡在发生深闭合后依然有一部分空泡持续附着，直至最终脱落。

3.2 不同密度比球体入水流体动力特性分析

(6)

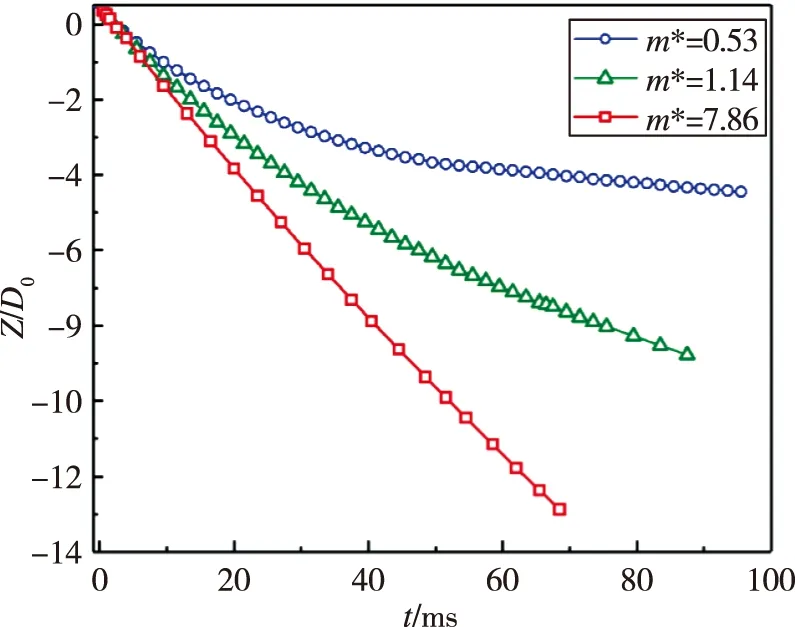
图12 不同密度比球体入水轨迹实验结果，Fr=10.9Fig.12 The sphere depth vs. time for the impact sequences of experimental results at Fr=10.9

(7)

(8)

(a)不同密度比球体流体动力系数随时间变化对比图，Fr=10.9

(b)不同密度比球体入水空泡夹断时流场结构，Fr=10.9图13 不同密度比球体流体动力系数对比及空泡夹断时流场结构Fig.13 Effect of sphere density ratio on hydrodynamic force coefficient upon impact and the flow structures when cavity pinches off

图13(a)展示了实验与数值不同密度比球体流体动力系数随时间变化对比结果，选取工况与图11相同，选取时间区间为1.5ms～75ms。此阶段内所有球体发生空泡夹断。总体上数值结果与实验结果吻合较好，尤其是对空泡夹断时流体动力系数陡增现象的捕捉。可以观察到入水初期各密度比入水球体的流体动力系数均呈现缓慢上升趋势，并且大小都比较接近，密度越大的球体所产生的受力系数略大一些。但很快随着时间的发展，密度越小的球减速越明显，造成对应的受力系数值以及增长的趋势都明显加大，尤其在空泡夹断和溃灭阶段，轻质球受力系数受到波动而陡增，橡胶球的也有明显的增加，而钢球由于重力较大整个过程受力系数的波动不明显，这种波动极其短暂，受力系数随着时间推进很快又趋于平稳。为进一步分析，结合图7(a)与图13(b)给出的其他两种密度球体入水空泡夹断时的流场结构云图可知，对于轻质球，空泡闭合在球的顶端并产生瞬间的闭合高压，同时由于完全沾湿而大大减小了所受的浮力与附加质量力，两者共同作用给了球体一个瞬间较大的推动作用。对于橡胶球和钢球，空泡夹断后球体携带的空泡体积快速减小，导致内部压强增大，因此也会对球体带来瞬间的推动。随着球体相对密度的增加，一方面夹断后球体所携带的空泡体积越来越大，内部压力变化相对更缓慢；另一方面自身的惯性也越来越大，抵抗空泡夹断所带来的扰动的能力也越来越强，因此波动也越发微弱。

图14给出了实验中密度比与傅汝德数对入水球体时均流体动力系数的影响，Fr区间为4.4～14.1，力的系数取t=0ms时刻到夹断前的平均值。可以观察到，时均流体动力系数对球体密度比敏感而受入水冲击速度影响较小。同一密度球体，随着入水速度增加，受力系数均呈现微弱的减小趋势。而相同入水速度下，密度越小的球体平均受力系数则显著增大。

图14 密度比与傅汝德数对时均流体动力系数的影响Fig.14 Effect of sphere density ratio and impact velocity on time-average hydrodynamic force coefficient to pinch-off

4 结论

本文采用实验与数值模拟相结合的方法开展了不同密度比的疏水性球体垂直入水研究，获得并分析了入水速度和球体密度对空泡形态、溅射水冠以及球体下落过程中流体动力特性的影响规律。主要结论如下：

1)随着入水冲击速度的增加，球体动能加大，入水空泡尺度增大并从准静态闭合空泡逐渐发展为深闭合及面闭合空泡，并且各状态的临界速度随着密度比的增加而减小。此外，空泡夹断后会形成闭合高压以及上下两股高速射流，射流的进一步运动加速了水面及球体附近空泡的溃灭。

2)较高的入水冲击速度会产生较强的溅射水冠。对于密度小于水的球体，球体表面固-液-气的三相接触线会在准静态空泡闭合时于球顶闭合，而密度大于水的球体接触线位置在空泡夹断前几乎无变化，稳定在距离球底0.35D0的位置。

3)球体带空泡航行阶段的时均流体动力系数随密度比的增加而减小，而随入水冲击速度的变化较小，同时空泡夹断会造成流体动力较大波动。