飞行器程控跟踪相控阵天线安装误差补偿技术

张德智, 胡 倩, 戴昌昊

(中国运载火箭技术研究院研究发展中心, 北京 100076)

0 引言

相控阵天线具有波束形状可定义、指向灵活、扫描速度快等特点[1]，在通信、雷达领域得到广泛应用。近年来，随着飞行器天基测控手段的普及和大容量星间多波束通信技术的推广[2]，相控阵天线在航天领域的应用也日益兴起，其中程控跟踪相控阵天线工作原理简单，可靠性高，受到了更多青睐。

近年来，飞行器上电源、热控技术不断进步，更高频段、更高密度、更高增益的相控阵技术逐步应用[3]。随着天线增益的提高，天线波束变得更窄，以阵元数量为512的Ka频段相控阵天线为例，天线波束宽度最窄处只有2.4°，对波束的指向精度要求很高，需要降低波束指向各个环节的误差来源。

1 程控波束指向误差来源

相控阵天线有自跟踪和程控跟踪两种方式。自跟踪方式通过提取接收阵列信号幅度，相位的和、差信息，从而获得误差控制信号，进行波束指向闭环控制，该方式对波束指向误差具有一定适应性。程控跟踪相控阵天线波控器利用飞行器平台组合惯导实时敏感的当前位置、姿态、速度信息以及预知的通信目标位置、速度信息，进行一系列波束指向角计算，将指向结果转换成波控码进行移相控制，最终实现合成波束指向通信目标，其对波束指向误差更加敏感。

波束指向误差来源主要有以下几个方面：天线和组合惯导的安装误差、组合惯导的测量误差、波控算法误差、移相控制误差、波束合成误差。其中波控算法误差、移相控制误差、波束合成误差为相控阵天线自身误差，李毓琦等[4]和隆锐[5]均提出了多种补偿方法。

安装误差和组合惯导的测量误差属于相控阵天线的输入误差。对于高精度组合惯导，飞行器位置测量精度可达10m以内，对于通信距离上万千米的星间链路，上述偏差可以忽略；姿态测量偏差可达0.1°以内，对波束指向影响很小。安装误差包括安装位置偏差和角度偏差，位置偏差为毫米量级，对波束指向结果影响很小，但角度偏差影响较大。组合惯导的安装角度偏差将影响飞行器姿态测量结果，相控阵天线安装偏差将影响波束指向基准。对于复材结构飞行器，设备安装角度偏差最大可达0.4°，对波束指向影响不可忽略。

2 安装误差测量方法

飞行器仪器设备安装角度偏差可以通过测量设备坐标系各轴与机体坐标系的角度偏差获取。定义相控阵天线坐标系为OaXaYaZa，定义组合惯导设备坐标系为OcXcYcZc，定义飞行器机体坐标系为OeXeYeZe。通过测量OaXaYaZa坐标系与OeXeYeZe坐标系的角度偏差可以获取相控阵天线安装角度偏差，通过测量OcXcYcZc坐标系与OeXeYeZe坐标系的角度偏差可以获取组合惯导设备安装角度偏差。

为获取高精度姿态偏差测量数据，本文采用了光学瞄准测量方法。测量设备包括1台G2000型摆式陀螺寻北仪(测量精度优于3″)和1台LeicaTM5100A型号的电子经纬仪(测量精度优于0.5″)。测量思路为：将光学设备可获取的东北天坐标系作为公共基准，通过测量各设备坐标系和东北天坐标系的角度偏差，推导出设备间的安装偏差。测量示意如图1所示。

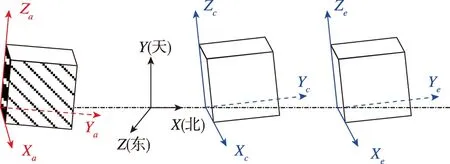
图1 各被测设备坐标系对应关系Fig.1 Coordinate system correspondence of the equipment under test

测量时首先在相控阵天线、组合惯导表面、飞行器粘贴立方棱镜，棱镜各轴与各设备坐标系定义的X、Y、Z轴平行。测量现场使用陀螺寻北仪建立方位基准，基准建立后使用光电经纬仪先瞄准立方镜，再跟寻北仪对瞄将北向基准引入，从而获取被测设备坐标系和东北天坐标系的角度偏差。测量内容如下：

测量Ka频段相控阵天线立方镜在Xa轴方向的方位角ψxa(Xa轴方向与北向夹角，北偏东为正)和俯仰角θxa(Xa轴方向与大地的不水平度，抬头向上为正)，再通过瞄准相控阵天线立方镜Ya轴方向，测量出Ya轴方向的俯仰角θya，通过上述3个角度可以确定相控阵天线相对于东北天坐标系的姿态。测量角度示意如图2所示。

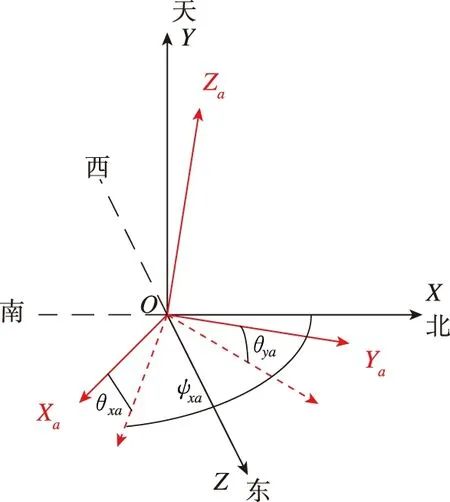
图2 Ka频段相控阵天线测量角度示意Fig.2 Schematic diagram of measurement angle of Ka band phased array antenna

同理测量组合惯导立方镜在Xc轴方向的方位角ψxc和俯仰角θxc，再通过瞄准组合惯导立方镜Yc轴方向，测量出Yc轴方向的俯仰角θyc，获得组合惯导姿态，从而完成惯导坐标系的标定；

同理测量飞行器立方镜在Xe轴方向的方位角ψxe和俯仰角θxe，再通过瞄准飞行器立方镜Ye轴方向，测量出Ye轴方向的俯仰角θye，获得飞行器姿态，从而完成机体坐标系的标定。

3 安装误差补偿方法

获取各设备相对于东北天的误差角度后，需要推导出相控阵天线相对于机体坐标系的姿态转换矩阵和组合惯导相对于机体坐标系的姿态转换矩阵，并将转换矩阵装定至对应设备以消除偏差。

设相控阵天线相对于东北天坐标系的姿态转换矩阵为La，机体相对于东北天坐标系的姿态转换矩阵为Le。如图2所示，从相控阵坐标系旋转至东北天坐标系的转换过程为：绕Ya轴逆时针旋转θma角，使得Xa轴落入XOZ平面(水平面)。绕新形成的Xa1轴顺时针旋转θya，使得Ya轴落入XOZ平面。绕新形成的Za2轴逆时针旋转ψxa角，使得Xa轴与X轴重合。绕X轴逆时针旋转90°，使得Ya轴与Y轴重合、Za轴与Z轴重合。因此，从相控阵天线坐标系到东北天坐标系的姿态转换矩阵为

La=Mx(90)·Mz(ψxa)·Mx(-θya)·My(θxa)

(1)

式中，Mi(x)代表着绕i轴旋转x角度的旋转矩阵。

(2)

同理，从机体坐标系至东北天坐标系的姿态转换矩阵为

(3)

式中，ψxa、ψxe、θya、θye的角度可直接测得，θma、θme的角度需要根据几何关系推算，经推导，当θxa、θya、θxe、θye较小时，有

(4)

(5)

将上述测量结果代入式(2)、式(3)中，可得La、Le，则相控阵天线坐标系到机体坐标系的姿态转换矩阵Lae为

(6)

Lae为消除了相控阵安装偏差后的姿态转换矩阵，将Lae矩阵装定至相控阵天线波控机，可以消除相控阵安装偏差对波控指向的影响。

同理，参照式(2)可以获取组合惯导相对于东北天坐标系的姿态转换矩阵Lc，则组合惯导坐标系到机体坐标系的姿态转换矩阵Lac为

(7)

Lac为消除了组合惯导安装偏差后的姿态转换矩阵，将Lac矩阵装定至组合惯导，可以消除组合惯导安装偏差对姿态测量的影响，从而降低对相控阵波控指向的影响。

4 效能评估

在某型无人机中，经光学瞄准测量获取的相控阵天线、组合惯导、机体相对于东北天坐标系偏差角度为

ψxa=+90°23′47″，θxa=0°23′48″，θya=-0°1′18″ψxc=+90°1′11″，θxc=-0°7′34″，θyc=+0°10′06″ψxe=+89°53′52″，θxe=-0°1′20″，θye=+0°3′01″

(8)

将上述角度代入式(1)～式(7)，求出相控阵天线相对于机体系的转换矩阵Lae和组合惯导相对于机体系的转换矩阵Lce，并将上述转换矩阵装定至相控阵天线和组合惯导

(9)

(10)

无人机飞行过程中,相控阵天线指向角度曲线见图3～图4，其中修正后指向数据通过无人机遥测数据获取。误差补偿前，最大指向偏差为0.6°。采取误差补偿后，实际测得的指向曲线比补偿前更接近理论曲线，最大指向偏差为0.2°，偏差值最大改善0.4°，有效减少了波束指向误差。

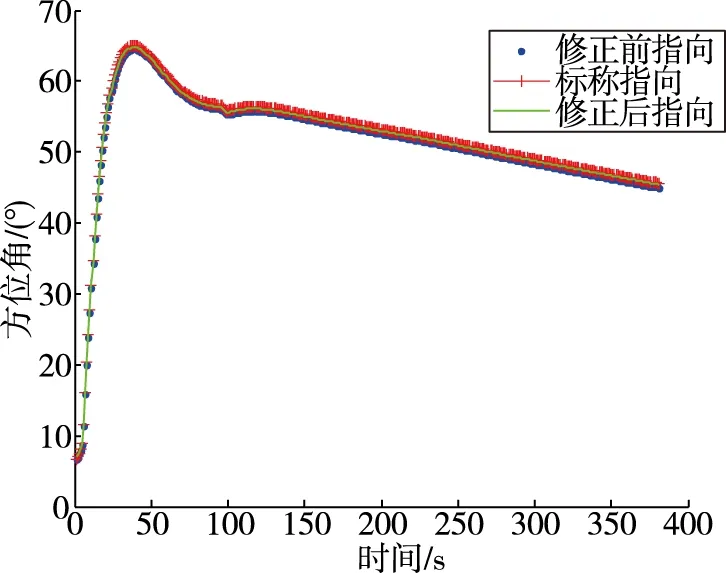
图3 安装误差补偿结果(全局)Fig.3 Installation error compensation results(whole)

图4 安装误差补偿结果(局部放大)Fig.4 Installation error compensation results(local zoom)

5 结论

本文提出的程控跟踪相控阵天线安装误差补偿方法，通过光学测量设备精确获取仪器设备的安装误差，利用测量数据推导出修正后的姿态转换矩阵，并装定至相控阵天线和组合惯导设备，以提高波束指向精度。通过某型无人机飞行任务实测验证，该方法可以有效提高波束指向精度。