模内微装配成型微型机械转动运动副可运动特性研究

周国发，郭 勇，陈 松

(南昌大学资源环境与化工学院，南昌 330031)

0 前言

聚合物微小机械系统制造产业化的共性技术瓶颈是微装配技术[1-4]，而模内微装配成型创新工艺逐渐成为解决这一技术瓶颈有效途径[5-7]，倍受学者关注。其成型过程如图1所示。先由可变组合模具左右两边的可移动滑块内的内圆柱孔形成一次成型微型轴的模腔，一次注射成型微型轴。待其冷却凝固后，再移动左右二边的滑块，由预成型轴的微装配面与可变组合模具重构二次成型微型块的模腔，二次注射成型微型块，并在模内同时实现二者的模内微装配。模内微装配成型集成型与装配于一体。模内微装配成型的技术关键是如何确保其成型加工的微型机械运动副具有可运动性能。然而在成型过程中，微型块的二次充填流动高温熔体与一次成型微型轴的微装配界面之间的高分子链扩散及缠结会诱发运动副装配界面的熔接粘附[8-10]，同时充填完毕后的微型块的冷却凝固定型会使其装配面形成冷却收缩自紧接触作用[11]。熔接粘附和冷却收缩自紧对微型机械运动副的运动会产生驱动摩擦阻力扭矩(见图2)，过大的驱动摩擦阻力扭矩可使运动副丧失可运动性能，形成废品。如何抑制运动副装配界面的熔接粘附，最大程度降低装配界面冷却收缩自紧接触压力就成为制备高性能微型机械运动副的技术关键。论文重点研究运动副装配界面冷却收缩自紧接触特性，明晰其关键调控参数，研究建立微型机械运动副形成可运动性能所需的最小驱动摩擦阻力扭矩的预测方法，研究具有重要的工程应用价值。

图1 模内微装配成型过程Fig.1 Molding process of in mold microassembly

图2 驱动摩擦阻力扭矩形成原理Fig.2 Forming principle of driving friction resistance torque

1 模内微装配成型运动副接触特性的模拟

1.1 模拟方法及技术路线

在微型块冷却凝固定型过程中，微型块与微型轴的微装配界面形成冷却收缩自紧接触的前提是：微型块在装配界面处的冷却凝固层厚度需超过某一临界厚度，微型块才具有足够的刚度来约束微装配界面的热黏弹塑性变形，使微型块与微型轴在微装配界面的热黏弹塑性变形不一致，由此而产生微装配界面过盈或间隙配合。而如何准确预测其微装配界面之间的装配过盈量所诱发的冷却收缩自紧接触压力是本文的关键科学问题。将初始形成自紧热黏弹塑性变形约束作用的临界固化层厚度时的温度场，作为计算运动副微装配界面冷却收缩自紧压力的初始温度场，计算追踪初始温度场的冷却降温过程中运动副微装配界面的热黏弹塑性接触变形，即可获得运动副微装配界面冷却收缩自紧接触压力。微型块冷却凝固定形过程涉及微型块聚合物材料的相变演化，其固相相态经历黏弹性高弹态→黏弹塑性玻璃态→弹塑性固态的连续相变演化过程，而如何建立综合反映温度和相变演化影响的固态聚合物材料的热黏弹塑性的应力-应变本构关系，是准确预测其热黏弹塑性变形的理论前提。基于上述分析，研究建立了图3所示的运动副微装配界面冷却收缩自紧接触过程模拟的技术路线。

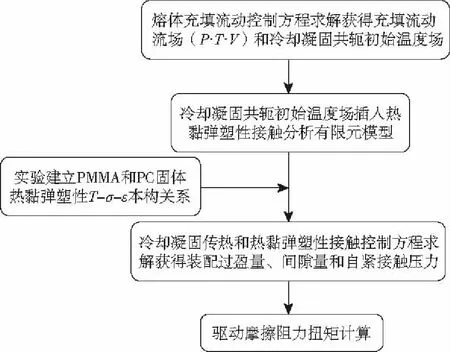
图3 模拟技术路线Fig.3 Technical route of simulation

1.2 模拟条件

图4 微型机械运动副有限元模型Fig.4 Finite element model of micro mobile mechanical pair

现以图1所示的微型圆轴和微型块组成的典型微型机械转动运动副的模内微装配成型过程为研究对象，研究成型加工的微型机械转动副的接触特性，其有限元模型见图4。微型圆轴尺寸为φ0.8×6 mm，微型块尺寸为4 mm×3.2 mm×8 mm。先模拟二次成型聚合物熔体的填充流动过程和冷却凝固过程，获得二次成型微型块形成临界固化层厚度的初始温度场，然后将此初始温度场插值导入微型机械运动副的热黏弹塑性接触分析的有限元模型中，进行传热和装配界面热黏弹塑性接触分析，获得二次成型微型块冷却凝固定型时其微装配界面的过盈量和冷却收缩自紧接触压力。

预成型微型轴采用聚碳酸酯(PC)材料，而二次成型微型滑块采用聚甲基丙烯酸甲酯(PMMA)材料，图5～图7分别是这2种材料的弹性模量、泊松比以及热膨胀系数与温度的关系曲线，图8为固态聚合物温度-应变-应力本构关系。二次成型PMMA熔体采用Cross-WLF本构方程[12]。模型参数见表1。

1—PMMA 2—PC图5 弹性模量与温度的关系Fig.5 Modulus of elasticity vs. temperature

1—PMMA 2—PC图6 泊松比与温度的关系Fig.6 Poisson ratio vs. temperature

1—PMMA 2—PC图7 热膨胀系数与温度的关系Fig.7 Thermal expansion coefficient vs. temperature

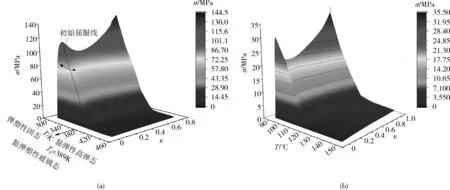
(a)PMMA (b)PC图8 PMMA和PC材料的热黏弹塑性温度-应变-应力本构关系Fig.8 Temperature-strain-stress thermal viscoelastic-plastic constitutive relation of PMMA and PC

(1)

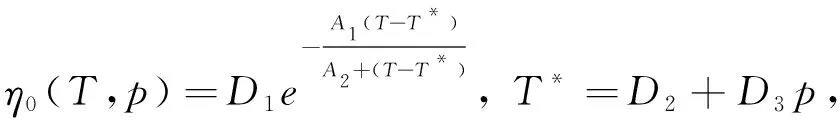
(2)

式中η——黏度,Pa·s

η0——零剪切黏度,Pa·s

n——流变指数

T——温度，K

τ*——产生剪切变稀特性的临界剪切应力, MPa

T*——参考温度，K

A1,A2——温度影响系数

D1——熔体在玻璃化温度下的零剪切率黏性系数，Pa·s

D2——玻璃化转变温度，K

D3——压力影响系数，K·Pa-1

表1 PMMA材料Cross-WLF本构方程材料参数Tab.1 PMMA material parameters of the Cross-WLF constitutive equation

1.3 二次熔体注射温度对初始温度场影响

固定其它工艺参数条件不变，仅人为改变二次成型注射温度，以此来研究二次成型注射温度对微装配界面形成收缩自紧的初始温度场的影响。工艺参数见表2。图9和图10分别为运动副初始温度场分布云图和二次成型注射温度与初始平均温度的关系曲线。研究表明：随着二次熔体成型注射温度提高，微型块的平均温度增高，而微型轴的平均温度降低。

表2 二次成型工艺参数Tab.2 Process parameters of secondary molding

图9 运动副初始温度场分布(T=503 K)Fig.9 Initial temperature field of motion pair

1.4 注射温度度对微装配界面收缩自紧接触特性的影响

1—微型块 2—微型轴图10 初始平均温度与注射温度的关系Fig.10 Initial temperature vs. injection temperature

图11为热黏弹塑性接触模拟的微装配界面装配过盈量与间隙量的云图。研究表明：在装配界面迎流面，二侧端区域为过盈配合，中间区域表现为间隙配合。而在背流面，二侧端区域为过盈配合，而随着二次成型注射温度提高，中间区域由间隙配合演化为过盈配合，且迎流面的过盈量和间隙量明显大于背流面。

(a)迎流面，463 K (b)迎流面，503 K (c)背流面，463 K (d)背流面，503 K图11 熔体注射温度对装配过盈量与间隙量的影响Fig.11 Influence of injection temperature on the maximum magnitude of interference and clearance

(a)迎流面，463 K (b)迎流面，503 K (c)背流面，463 K (d)背流面，503 K图12 注射温度对收缩自紧接触压力的影响Fig.12 Influence of injection temperature on self tightening contact pressure

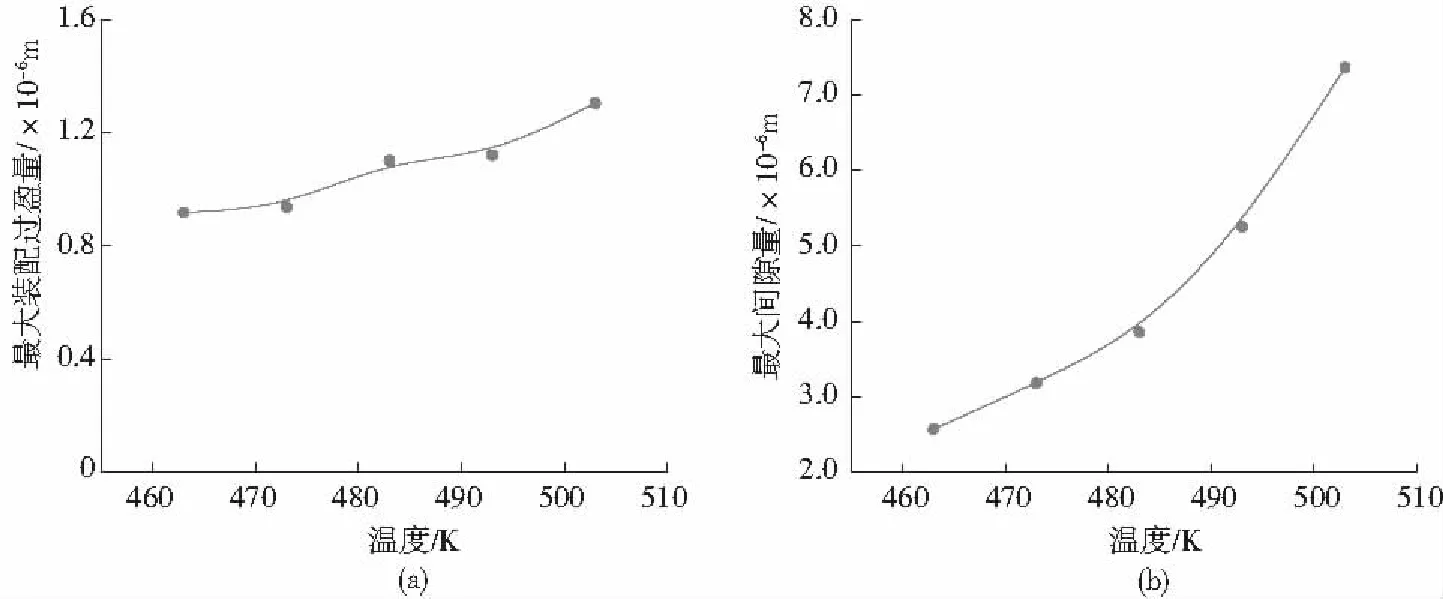
(a)最大装配过盈量 (b)最大间隙量图13 最大装配过盈量和最大间隙量与注射温度的关系Fig.13 Relation of the maximum magnitude of interference and clearance vs. injection temperature

图12为二次成型注射温度对微装配界面冷却收缩自紧接触压力的影响。研究表明：运动副微装配界面二侧端区域的冷却收缩自紧接触压力明显大于中间区域。在装配界面迎流面中间区域，由于均为间隙配合，则其自紧接触压力为零。而在背流面中间区域，随着二次成型熔体注射温度提高，其配合由间隙配合逐渐演化为过盈配合，因而其自紧接触压力逐渐增大。图13为注射温度与微装配界面最大过盈量和最大间隙量的关系曲线。研究表明：运动副微装配界面的最大装配过盈量和间隙量均随着二次成型注射温度提高而增大，当二次成型熔体注射温度由463 K增至503 K，其最大装配过盈量由9.17×10-7mm增至1.24×10-6mm，增幅35.2 %，而最大装配间隙量由2.45×10-6mm增至3.83×10-6mm，增幅为56.3 %。由此可见降低二次成型注射温度，有利于提高模内微装配成型运动副的配合精度和可运动性能。

通过后处理软件，可计算出微装配界面的面积平均收缩自紧接触压力，再由滑动摩擦公式计算得到微型机械运动副的驱动摩擦阻力扭矩，其中PMMA与PC材料副的滑动摩擦因数取为0.3。图14是运动副微装配界面平均收缩自紧接触压力和驱动摩擦阻力扭矩与注射温度的关系。研究表明：自紧接触压力和驱动摩擦阻力扭矩均随着二次成型注射速度提高而增大。当二次成型注射温度由463 K增至503 K时，微装配界面平均收缩自紧接触压力由778 364 Pa增至1 197 766 Pa，增幅为53.9 %，而其驱动摩擦阻力扭矩由2.35 N·mm增至3.61 N·mm，增幅为53.6 %。综上可知，降低二次成型注射温度，有利于大幅减小微装配界面的收缩自紧接触压力和微机械转动运动副获得可运动性能的最小驱动摩擦阻力扭矩，并提高其可运动性能。

(a)平均自紧接触压力 (b)驱动摩擦阻力扭矩图14 平均自紧接触压力和驱动摩擦阻力扭矩与注射温度的关系Fig.14 Average self tightening contact pressure and driving friction resistance torque vs. injection temperature

图15为在驱动摩擦阻力扭矩作用下，运动副初始形成转动时， PC微型轴当量应力分布云图，图16为其最大von-Mises当量应力与二次成型注射温度的关系曲线。研究表明：当二次成型注射温度由463 K增至503 K时，其PC微型轴的最大von-Mises当量应力由40.6 MPa增至62.4 MPa，而PC材料在常温下的断裂强度为54.8 MPa。由此可见，二次成型注射温度不宜超过483 K，否则运动副形成初始运动时，PC微型轴的最大von-Mises当量应力会超过PC材料的断裂强度，易导致微型轴产生断裂失效。

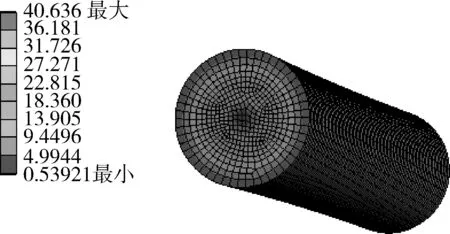
图15 驱动阻力矩作用下微型轴的当量应力云图(T=463 K)Fig.15 Cloud chart of von-Mises equivalent stress of micro shaft

图16 最大当量von-Mises应力与成型温度的关系Fig.16 Relation of the maximum von-Mises equivalents stress under driving friction resistance torque vs. injection temperature

2 结论

(1)基于实验建立的PMMA和PC固体的温度—应变—应力热黏弹塑性本构关系，构建了模内微装配成型微型机械运动副冷却收缩自紧热黏弹塑性接触过程的模拟仿真方法，该方法能准确预测微机械转动运动副获得可运动性能的最小驱动摩擦阻力扭矩；

(2)运动副微装配界面的最大装配过盈量和间隙量与二次成型注射温度呈正关联关系，当二次成型注射温度由463 K增至503 K，其最大装配过盈量由9.17×10-7mm增至1.24×10-6mm，增幅35.2 %，而最大装配间隙量由2.45×10-6mm增至3.83×10-6mm，增幅为56.3 %；降低二次成型注射温度，有利于提高其运动副的装配配合精度，并改善其运动性能；

(3)运动副微装配界面的冷却凝固收缩自紧接触压力和驱动摩擦阻力扭矩均与二次成型注射温度呈正关联关系；当二次成型注射温度由463 K增至503 K时，其平均冷却收缩自紧接触压力由778 364 Pa增至1 197 766 Pa，增幅为53.9 %，而其驱动摩擦阻力扭矩由2.35 N·mm增至3.61 N·mm，增幅为53.6 %；降低二次成型注射温度，可大幅减小微机械转动运动副获得可运动性能的最小驱动摩擦阻力扭矩。