新媒体视角下朱利亚集合生成形态研究

（祥明大学 韩国 首尔 110-743）

新媒体概念的出现，使得艺术作品本身的定义不再决定于它的实体形式，而是更多的在于它的形成过程。分形艺术作为新媒体中的一种艺术类别，它不同于普通的电脑绘画，而是由计算机程序生成，将抽象的数学公式转变成充满神秘感的艺术性创作。

一、分形，一种新的几何语言

分形原意是指“不规则的、分数的、支离破碎的”物体。人类在认识自然、改造自然的过程中，用以描述客观世界的几何学是欧几里德几何学、解析几何学等近似线性的处理方式。虽然使很多理论和实际问题得到了解决，但是随着社会和科学技术的发展，已经显露出它的局限性。自然界大部分不是有序的、平衡的、稳定的和确定性的，而是处于无序的、不稳定的、非平衡的和随机的状态之中，它存在着无数的非线性过程[1]。

自20世纪70年代以后，科学家开始跨入无序的大门,纷纷探索各类不规则现象。云团不是球体、山岭不是锥体、海岸线不是圆周、树皮并不光滑、闪电更不是沿直线传播[2]。这些不规则的形态很难用传统欧氏几何的方式加以描述，人类需要新的几何语言。正是在这种情境之下,法国数学家曼德勃罗特创立了研究复杂现象的非线性科学——分形。经过短短四十几年的发展，分形在自然科学和社会科学领域得到极大关注，并对艺术领域产生了一定的影响[3]。已成为一门描述自然界中许多不规则事物的规律性学科。

二、朱利亚集合解读

朱利亚集合是在复平面上形成分形的点的集合，在分形理论中具有重要地位，它用分形维数的视角和数学方法来描述和研究客观事物，是数学与艺术的完美结合。朱利亚集合可以由以下公式进行反复迭代得到：

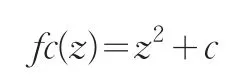
对于固定的复数c，取某一z值（如z=z0），可以得到序列

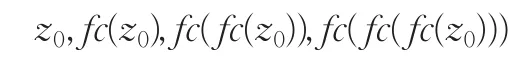
这一序列可能发散于无穷大或始终处于某一范围之内并收敛于某一值。我们将使其不扩散的z值的集合称为朱利亚集合[4]。

三、控制参数对朱利亚集合形态的影响

在新媒体时代，视觉艺术随着数字技术的发展，开始寻求更多的表现形式。朱利亚集合与控制参数——逃逸时间K、逃逸半径M的数值紧密相关，是从数字化设计出发的一种新的设计思潮。下面将运用Microsoft Visual C++程序，以二次朱利亚集合为例作具体的分析。

（一）逃逸时间K对朱利亚集合形态的影响

在Microsoft Visual C++程序中，设定绘图范围a–1 600，b–1600，逃逸半径 M 500，实部p 0.32，虚部q 0.043。

逃逸时间K取值K1,K20,K50,K100,K200,K500，K1000,K10000。共生成八幅图像。

图1 ：不同的逃逸时间K所对应的二次朱利亚集合

分析结果整理如下：

从直观上可以看出，逃逸时间K的取值由小变大时，朱利亚集合由不规则的边缘轮廓逐渐转变为具有精细结构的复杂图像。

在生成朱利亚集合的过程中，所需时间随着K值的增大而变长。这可能与逃逸时间K取值增大，朱利亚集合点的迭代次数增多，点逃逸出去所需要的时间增加有关。

（二）逃逸半径M对朱利亚集合形态的影响

在Microsoft Visual C++程序中，设定绘图范围a–1600，b–1600，逃逸时间K 100，实部p 0.32，虚部q 0.043。

逃逸半径M取值M1,M10,M50,M100,M500,M1000,M10000,M100000。共生成八幅图像。

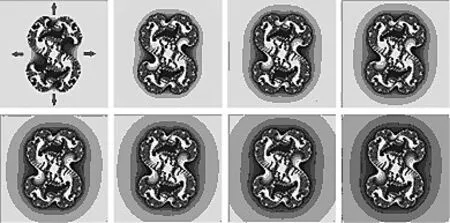
图2 ：不同的逃逸半径M所对应的二次朱利亚集合

分析结果整理如下：

总体来说，逃逸半径M的取值对朱利亚集合形态的影响不大。逃逸半径M在取值1以后，图像变化过程缓慢，很难直接分辨。但是将这八幅图像连续播放后可以明确地看出，随着逃逸半径M取值增大，朱利亚集合的点，缓慢向发散区逃逸，原本向内凹陷处（图中红色箭头标记处）逐渐向外膨胀，同时图像亮度也逐步降低。

四、朱利亚集合的形态特征

（一）自相似性

自相似性是分形几何的重要特征，它是自然界的普遍规律之一。在不同的尺度下观察朱利亚集合，可以看到其部分与部分之间的精细结构相似，一样曲折、琐碎、纷乱、不规整、不光滑，并且，部分与整体也具有一样的复杂性。这使得生成的朱利亚图形具有节奏和韵律感。

（二）标度不变性

在朱利亚集合上任选一局部区域，对其进行放大，这时得到的放大图像又会显示出原图的形态特性，因此，对于朱利亚集合，不论将其放大或缩小，它的形态、复杂程度、不规则等各种特性均不会发生变化[5]。标度不变性与自相似性是密切相关的，具有自相似的结构（或图形），一定会满足标度不变性[6]。

（三）嵌套性

朱利亚集合具有复杂的层次结构，蕴含着无穷的嵌套关系。整体中任何点都是结构的一个分支点，整体中的任何一部分又是它自身的整体，尺度越来越小，精细度却越来越高。这种嵌套性的复杂结构给朱利亚集合带来了画面的丰富性，赋存着无尽的创造力。

（四）随机性

自然界产生的形体不可能像数学所产生的计算结果一样精确无误，大多数是不规则的、随机性的。在计算机生成朱利亚集合的过程中，随机性产生的“不可预测”是突破设计师惯性思维的重要因素，同时也赋予了朱利亚集合形态的多样化。

结语

本文以朱丽亚集合为中心，运用Microsoft Visual C++程序，分析并探讨了控制参数对朱利亚集合形态的影响及其形态特征。研究结果表明，朱丽亚集合与逃逸半径M、逃逸时间K的参数紧密相关，参数的改变会使朱丽亚集合的形态产生变化。朱丽亚集合具有自相似性、标度不变性、嵌套性、随机性的形态特征。

在新媒体时代，视觉艺术随着数字技术的发展更加趋于数字化、虚拟化和多样化，技术的变革必将引起艺术形式的创新。分形揭示了隐藏在复杂现象背后的局部与整体的本质联系和运动规律，体现出“非理性的、非总体性、非线性的”思维倾斜。作为一种新兴的数字艺术，其独特的构成形式、空间形态以及动态样式，为视觉艺术提供了更为广阔的思维空间和创作方式，符合数字化设计的发展趋势。