微型谐振气体传感器多场耦合非线性振动特性分析

付晓瑞，党亚辉，许立忠

(燕山大学 机械工程学院，河北 秦皇岛 066004)

微机电系统(Micro-Electro-Mechanical System，MEMS)主要包括微传感器、微执行器和处理电路三部分[1-2]。微传感器作为MEMS器件中的一个重要组成部分，在机器人、智能设备、医疗设备等高科技领域中得到广泛应用，已成为国内外微机电系统领域中一个重要研究方向。传感器根据其工作原理又可分为电容式、电阻式和谐振式三种，其中微谐振传感器输出的为不易失真的频率信号，不受距离因素的影响，因此受到广泛关注。微型谐振气体传感器尺寸小、结构简单、灵敏度高、稳定性好，更符合气体传感器智能化、高灵敏化、集成化、微型化的发展方向。

近年来，国内外学者对微谐振气体传感器进行了大量的研究工作。20世纪60年代，ZnO半导体气体传感器研制成功并作为一种新兴产品投入市场[3-4]。2001年，Lange等[5]开发了一种集成在芯片上的热激励共振气体检测系统，其中热敏电阻用作谐振驱动器，惠斯通电桥用于悬臂梁振动的检测。Fadel等[6]开发了用于检测挥发性有机化合物(Volatile Organic Compound，VOC)的质量敏感性气体传感器，验证了毫米尺寸和微米尺寸悬臂之间的噪声在集成传感器设计中不可忽略。Thomas等[7]开发了微悬臂梁阵列，进行亚微摩尔浓度下细菌病毒T5的定量质量测量实验。李鹏等[8]设计了一种高分辨率压阻检测式硅微悬臂梁谐振式传感器。张建等[9]研究了范德华力对硅基微悬臂梁抗黏附稳定性的影响。Zimmermann等[10]设计制作出用于检测具有挥发性的有机气体的高度集成气体传感器。李强等[11]利用旋转涂胶的方法制备了酞菁铜薄膜材料，经研究发现酞菁铜具有良好的气敏特性。刘丽丽等[12]研究了一种新型微气体传感器结构,并利用仿真软件对该结构的传感器进行了优化与相关研究。Xu等[13]引入气体吸附的化学反应动力学方程，建立了机械-化学耦合动力学模型，研究了微型谐振气体传感器的时变特征。总之，国内外已经取得一系列有关微型谐振气体传感器的研究成果。然而，随着谐振式传感器尺寸的不断减小，极板间的分子力、尺寸效应和热应力对微谐振梁振动特性的影响变得不能忽略[14]，同时，谐振子处于多场耦合的环境下，因此对悬臂梁多场耦合振动的研究具有重要意义。目前，国内外对于考虑温度影响的微型谐振气体传感器多场耦合动力学问题的研究较少。为此，本文建立微型谐振气体传感器的机械-化学-分子力-温度四场耦合动力学方程，分析分子力和温度对气敏传感器固有频率、瞬时频率以及时域动态响应的影响规律，为该种传感器进一步的微型化和智能化奠定理论基础。

1 动力学方程

本文采用的微谐振子多场耦合动力学模型，如图1所示。分为底座和悬臂梁两个部分，底座和悬臂梁由单晶硅制成，悬臂梁单晶硅部分厚度为h；悬臂梁表面蒸发镀导电层，厚度为h2；在导电层表面利用旋转法涂上厚为h1的酞菁铜敏感层。当传感器的周围环境内含有被测气体时，被测气体分子以速度K1附着在被敏感层上，同时被测气体分子以速度K2从附着层脱落，最后与环境中气体浓度达到平衡状态，如图1所示。K1为气体附着在敏感层速度常数，K2为气体脱离敏感层速度常数。

将梁的中轴线作x轴，将对称面内与x轴垂直向上的方向取作y轴。由于采用的悬臂梁是细长梁，可以忽略其剪切变形和截面绕中性轴旋转的惯性效应。梁只有在y轴方向的位移y(x,t)，底座和悬臂梁下表面距离为u。悬臂梁长为l，宽为b，密度为ρ，弹性模量为E，截面面积为S，作用在梁上沿y轴的单位长度动载荷为Δq(x,t)。

根据振动理论得到梁的动态弯曲振动方程[15]

(1)

Δq包括电场力和分子力，即

Δq=Δq0+Δqr

(2)

其中动态单位长度的范德华力为[16]

(3)

式中：A为Hamaker常数，A=10-19J。

真空下动态单位长度开西米尔力为

(4)

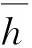
因位移变化引起单位长度动态电场力为

(5)

当将传感器放在含有被测气体环境中时，气体吸附的化学反应动态平衡方程为

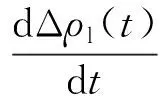
(6)

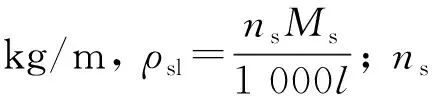
由敏感层中材料分子个数不变可知

ns+Δns=ns0

(7)

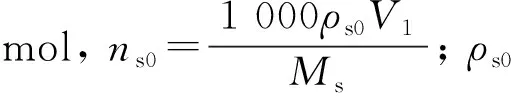
联立式(6)和式(7)，并积分可得敏感层吸附质量密度变化表达式为

(8)

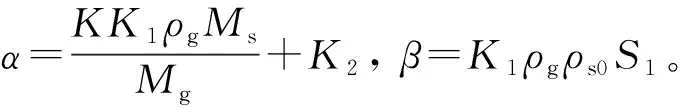
梁上各点的非线性位移应变关系为

(9)

y(x,y,t)=y(x,0,t)=y(x,t)

(10)

梁上的任一点的格林应变为

(11)

当考虑温度载荷时，梁中沿轴向的正应力

σ=E(ε-αT)

(12)

式中：ε为格林应变；α为热膨胀系数；T为温度变化量。

将轴向的正应力沿y轴进行积分，求和得到轴向合力和合力矩

(13)

(14)

式中：hp≈h1+h2；hb=h；Eb=E,Ep为复合层弹性模量，由参考文献[17]可得。

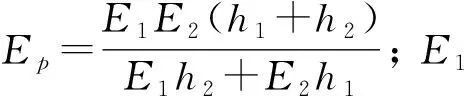
将式(13)和式(14)代入弯曲振动方程可得

(15)

将式(15)简化为

(16)

其中，

F=bT(Epαphp+Ebαbhb)

考虑范德华力情况下动态方程为

(17)

考虑开西米尔力情况下动态方程为

(18)

令Δy=φ(x)q(t)代入式(8)并进行变换可得

(19)

(20)

其中，

ρl0=ρbh+ρtbht+ρs0bh1

解模态方程式(19)，得各阶固有频率为

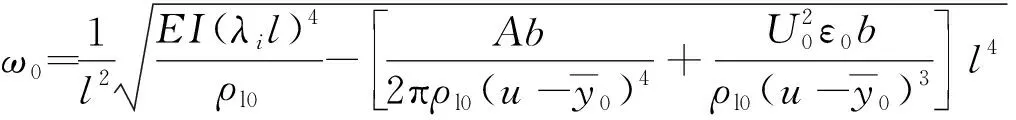
(21)

同理得考虑开西米尔力时的各阶固有频率为

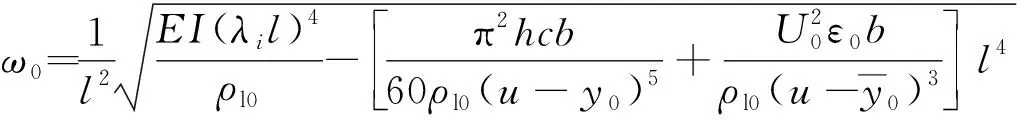
(22)

式中：λ1l=1.875;λ2l=4.694;λ3l=7.855;λ4l=10.996。

与之对应的各阶模态函数为

φi(x)=cosλix-chλix+ηi(sinλix-shλix) (i=1,2,3,4,L)

(23)

其中，参数ηi定义为

式(20)舍去化学项得到

(24)

将q(t)展开成ε的幂级数如下

q=q0+εq1+ε2q2+L

(25)

将系统自由振动频率ω展开成ε的幂级数如下

(26)

引入变量τ=ωt得

(27)

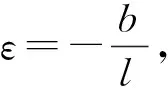
(28)

将τ=ωt代入式(28)中得

(29)

可得

(30)

令ε的同次幂项的系数化和为零，可得

(31a)

(31b)

(31c)

各方程的初始条件如下，A为广义坐标初值

(32)

从零次近似方程式(31a)和初始条件式(32)解出

q0=Acosτ

(33)

将式(33)代入式(31b)，可得

(34)

为避免式(34)的解中有久期项，使cosτ系数等于零，可得

σ1=0

(35)

将式(32)和式(33)代入式(34)中，可得

(36)

将式(33)和式(36)代入(31c) ，可得

(37)

为避免次式(37)的解中有久期项，使cosτ的系数等于零，可得

(38)

将式(36)和式(38)代入式(37)，可得

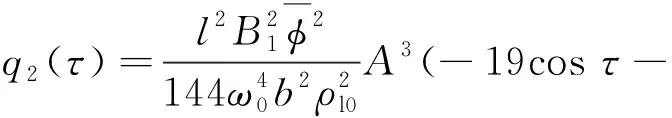
(39)

将式(33)、式(36)和式(39)代入式(25)，可得

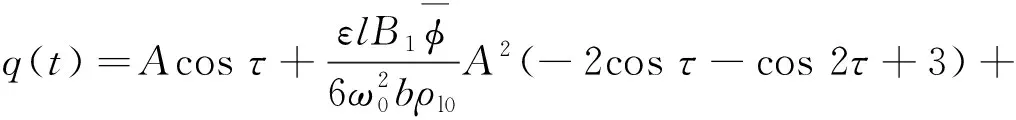
(40)

将式(35)和式(38)代入式(26)，可得

(41)

悬臂梁上任意一点某时刻的位移表达式为

y=y0+Δy=y0+φ(x)q(t)

(42)

式中：y0为初始静态位移。

为求解瞬时频率，可引入Hilbert变换，对任意的时间序列x(t)，它的Hilbert变换为

对q(t)做Hilbert变换，得到

(43)

将瞬时频率定义为

(44)

可得到悬臂梁瞬时频率表达式为

ω=(1+εC1+ε2C2)ω0

(45)

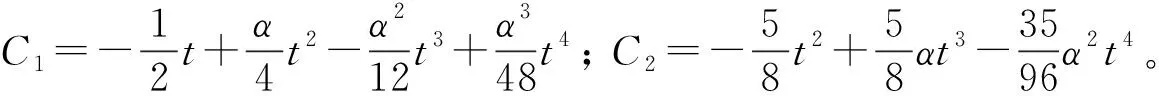
2 实例计算与分析

2.1 频率特性

微型谐振气体传感器主要参数，如表1所示。待测乙醇气体浓度ρg=0.000 1 kg/m3，利用式(21)、式(22)可得传感器在考虑与不考虑分子力情况下各阶固有频率，如表2所示。其中ω1为不考虑分子力时固有频率，ω2为考虑范德华力时固有频率，ω3为考虑开西米尔力时固有频率，η1为考虑范德华力时与不考虑分子力时相对偏差，η2为考虑开西米尔力时与不考虑分子力时相对偏差。将第一阶固有频率代入式(45)可以得到不同情况下的瞬时频率响应曲线，如图2所示。假设环境温度30 ℃，比较考虑和不考虑热应力情况下瞬时频率与初始固有频率差值随时间t的变化，图3(a)为考虑范德华力情况下的变化曲线，图3(b)为考虑开西米尔力情况下的变化曲线，由表2、图2和图3可知：

表1 系统计算参数Tab.1 System parameters

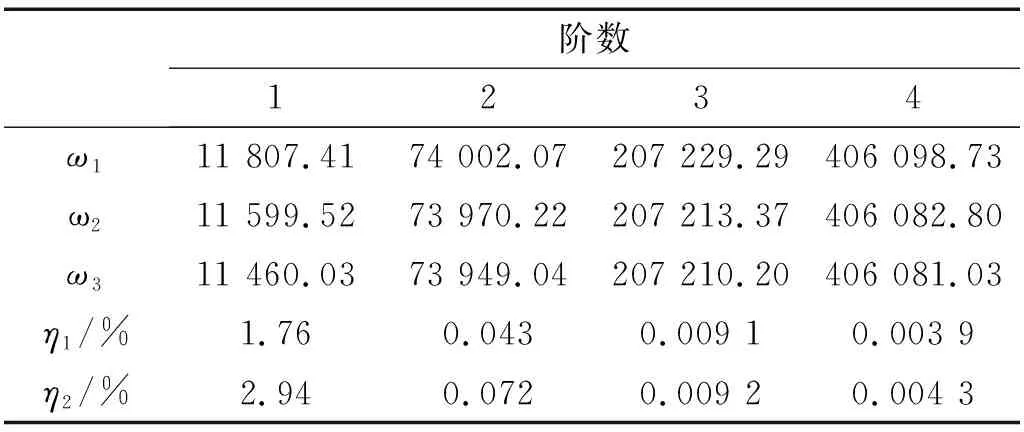
表2 各阶固有频率Tab.2 The natural frequency of each order Hz

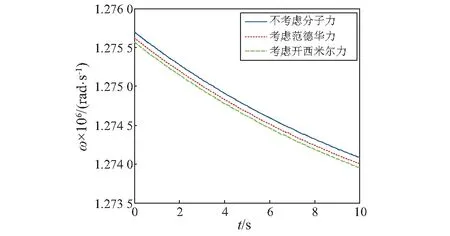
图2 瞬时频率响应曲线Fig.2 Instantaneous frequency response curve

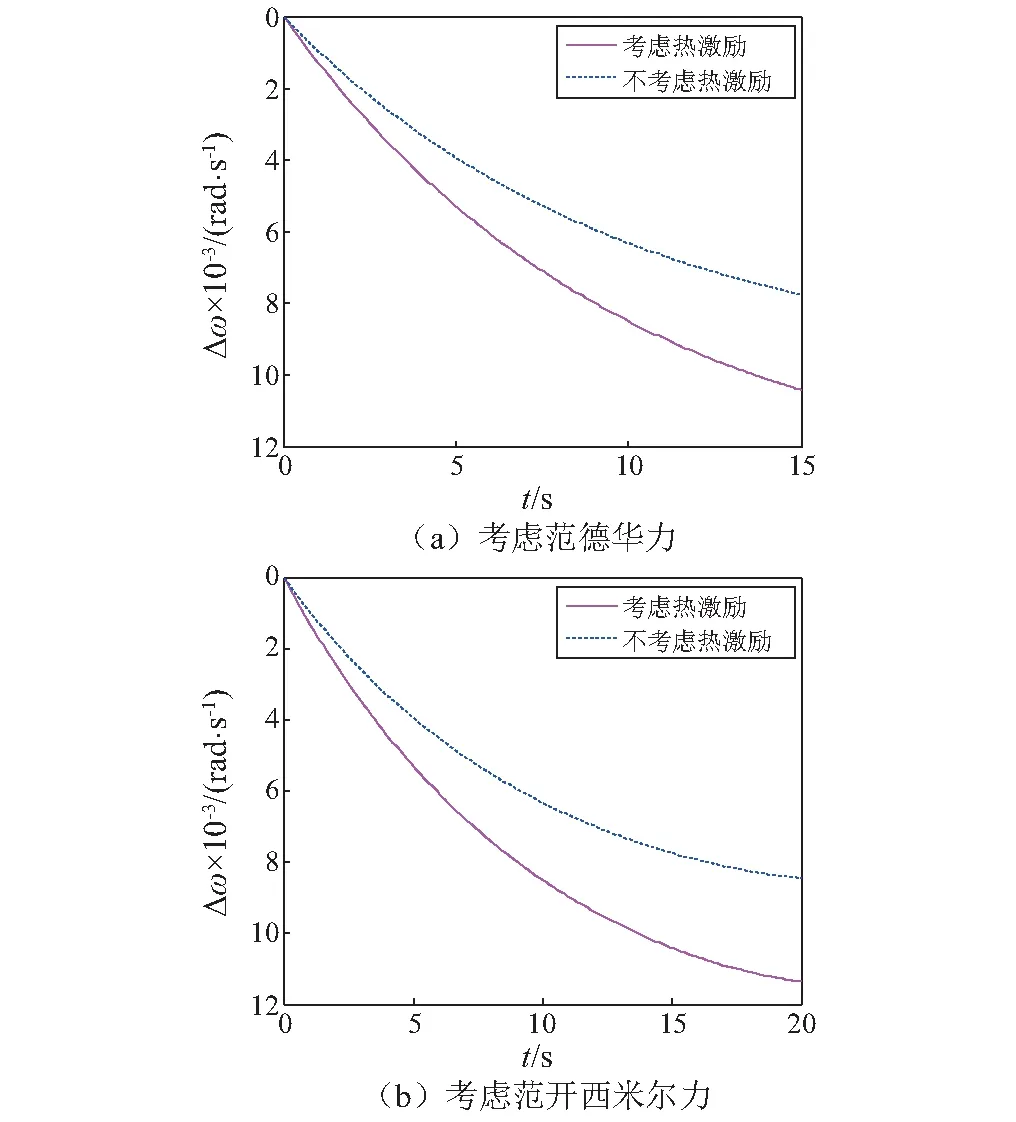
图3 瞬时频率差变化曲线Fig.3 Difference of instantaneous frequency

(1)考虑分子力时，微型谐振气体传感器的固有频率比不考虑分子力时要小，而且考虑开西米尔力的情况比考虑范德华力情况时固有频率下降更为明显。随着阶次的增加范德华力对传感器的固有频率的影响减弱，第一阶时考虑范德华力时的相对偏差为1.76%，而考虑开西米尔力时相对偏差为2.94%。而第四阶相对偏差分别为0.003 9%和0.004 3%，因此对于低阶次固有频率，分子力的影响不可忽略。

(2)传感器的固有频率随着时间的延长，逐渐下降。这是由于谐振子不断吸附酒精气体分子而导致的谐振子质量不断增加的结果。考虑分子力与不考虑分子力情况相比，谐振子固有频率变化趋势一致，但是每一时刻对应的固有频率不同。

(3)考虑热激励时谐振子固有频率随时间下降的速度更快，频率下降幅度更大。其中考虑开西米尔力情况下谐振子固有频率受热激励的影响更为显著。

2.2 时域分析

为了研究范德华力和开西米尔力对悬臂梁振动时域动态响应的影响，将悬臂梁顶端处分别将考虑范德华力和开西米尔力时的动态响应与不考虑分子力时的动态响应进行求差。图4为动态响应差随悬臂梁长度变化规律，图5为动态响应差随悬臂梁与基体间隙变化规律。可以得知：

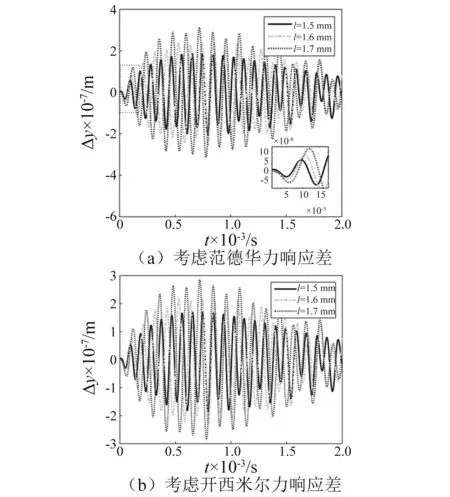
图4 响应差随悬臂梁长度变化Fig.4 Difference of the vibrating amplitudes as length

(1) 分别考虑范德华力和考虑开西米尔力时的响应差随着时间的增加，响应差幅值先增大后减小，表明两种分子力对悬臂梁多场耦合时的时域动态响应的影响随时间变化成周期性变化。

(2) 随着悬臂梁长度增大，两种情况的响应差的幅值增大，且当长度变化时响应差的幅值变化较大，因此，响应差对于悬臂梁长度的变化敏感。

(3) 随着悬臂梁与基体的间隙变小时两种情况的响应差幅值变大，且随着初始间隙变化时响应差变化剧烈，因此对于初始间隙较小时，两种分子力对悬臂梁多场耦合时的时域动态响应影响较大，不可忽略。

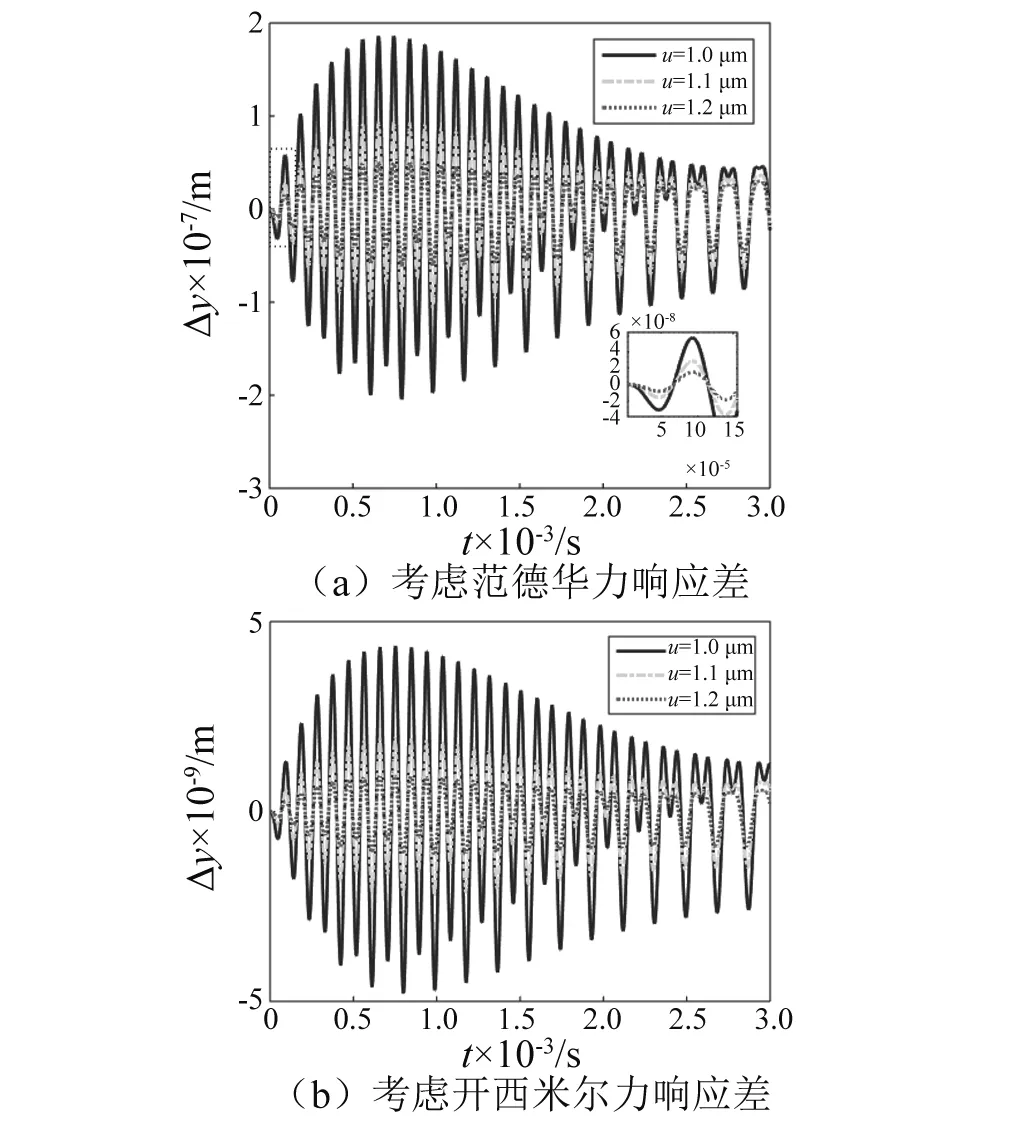
图5 响应差随悬臂梁间隙变化Fig.5 Difference of the vibrating amplitudes as gap

2.3 实验分析

悬臂梁振动频率是谐振式气体传感器的关键参数，直接决定了气体传感器的性能，因此，研究悬臂梁的频率特性非常重要。为了验证上述关于悬臂梁振动频率理论分析的正确性，利用光刻、腐蚀以及镀膜等其他微机械加工工艺，制作出悬臂梁谐振子以及微谐振气体传感器，如图6 所示。利用自行设计研发的测试系统进行振动频率测试。

图6 微型谐振子及气体传感器Fig.6 Micro resonator and gas sensor

本实验采用静电激励-电容检测的方法进行振动频率的测量，当静电驱动的频率接近悬臂梁固有频率时，悬臂梁发生共振，此时位移响应出现极值，从而输出的电压信号也最大，通过观察输出的幅频图中极值点所对应的频率来确定悬臂梁的固有频率。静电激励-电容检测电路如图7所示，试验现场照片如图8所示，试验结果如图9所示。得到扫描频率等于11.579 kHz时信号幅值最大，可以判断谐振子固有频率在11.579 kHz附近，表3为实验结果与与理论分析结果的比较，由表3可以得知，考虑范德华力时，理论结果与实验结果相对偏差为1.34%，考虑开西米尔力时相对偏差为1.67%，不考虑分子力时相对偏差为1.74%，从而验证了理论分析的正确性，同时验证了当传感器尺寸足够小时，分子力的影响不可忽略。

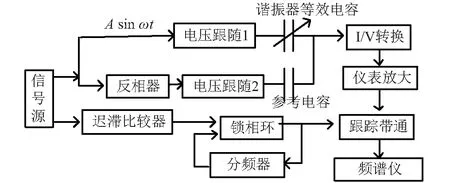
图7 开环检测系统Fig.7 Open loop detection system

图8 实验现场图Fig.8 Experimental site map

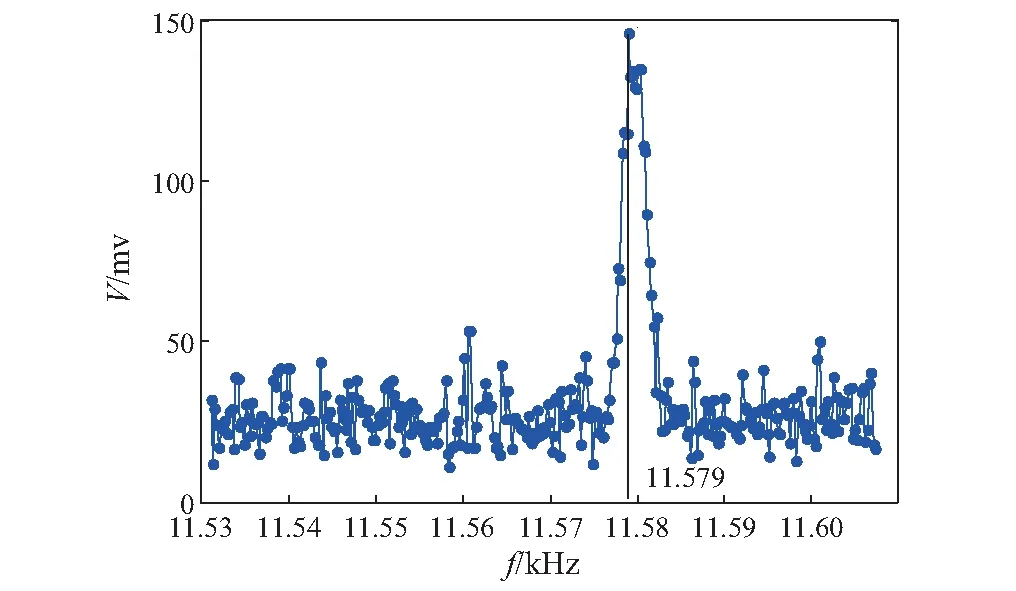
图9 开环扫频曲线Fig.9 Open loop sweep curve表3 实验结果与理论值比较Tab.3 Comparison of experimental results and theoretical values

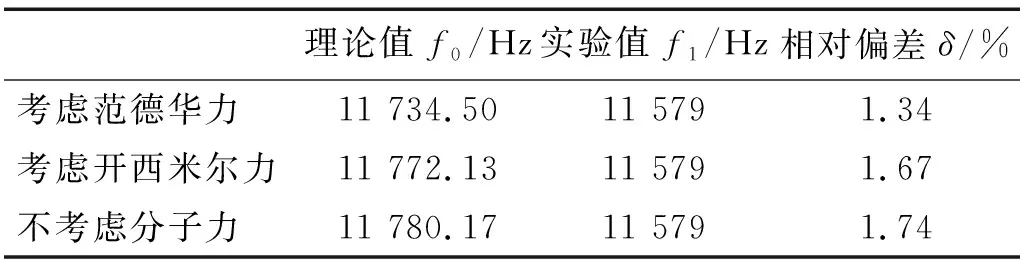
理论值f0/Hz实验值f1/Hz相对偏差δ/%考虑范德华力11 734.5011 5791.34考虑开西米尔力11 772.1311 5791.67不考虑分子力11 780.1711 5791.74

3 结 论

本文建立了微型谐振气体传感器机械-化学-分子力-热应力四场耦合动力学方程，并利用多尺度法求出谐振子固有频率表达式。研究了谐振子固有频率随分子力、吸附气体浓度以及温度的变化规律，分析了系统参数对悬臂梁时域响应差的影响，得知，当传感器中谐振子尺寸足够小时，分子力的影响不可忽略且当悬臂梁间隙较小、长度较大时，分子力对传感器低阶次固有频率和时域响应的影响较大。利用微机械加工技术制造出的微型气体传感器，并研发出开环测试系统，进行了扫频实验，得到微传感器的固有频率，与分析结果接近，验证了理论分析的正确性。