基于密度峰值聚类算法的模态参数识别
王飞宇,胡志祥,黄 潇
(1.合肥工业大学 土木与水利工程学院,合肥 230009; 2.中国电子科技集团公司第三十八研究所,合肥 230088)
仅通过系统的响应信号识别模态参数一直是个有挑战性的研究。盲源分离法(Blind Source Separation, BSS)已经被广泛的应用于模态分析领域。Kerschen等首次将单模态信号作为BSS算法中的源信号,并利用独立分量分析(Independent Component Analysis,ICA)提取多个单模态信号,得到结构每阶模态振型。与传统时域方法相比,BSS具有无需先验信息、计算简单、非参数化等优点。随后,一些学者提出了新的盲源分离方法都得到较好的结果,例如:二阶盲辨识方法(Second Order Blind Identification, SOBI)、多源提取方法(Algorithm for Multiple Unkown Signals Extraction, AMUSE)等。
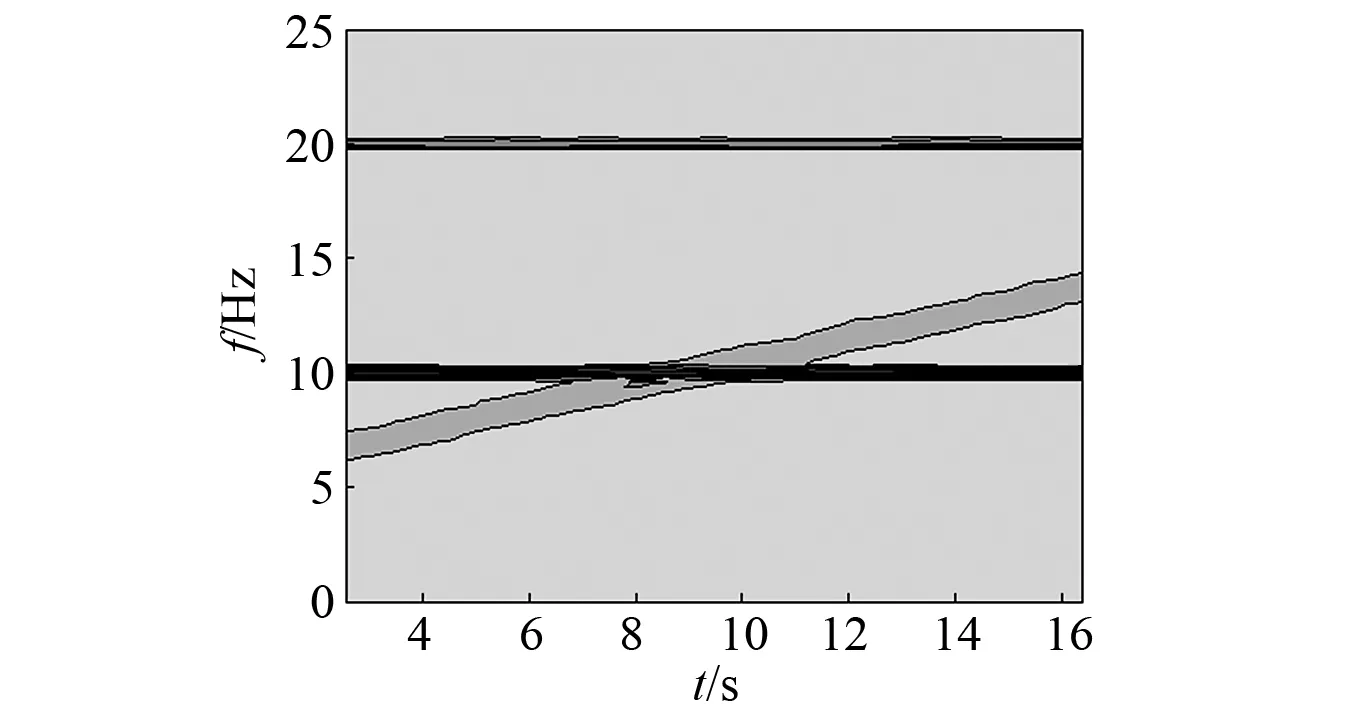
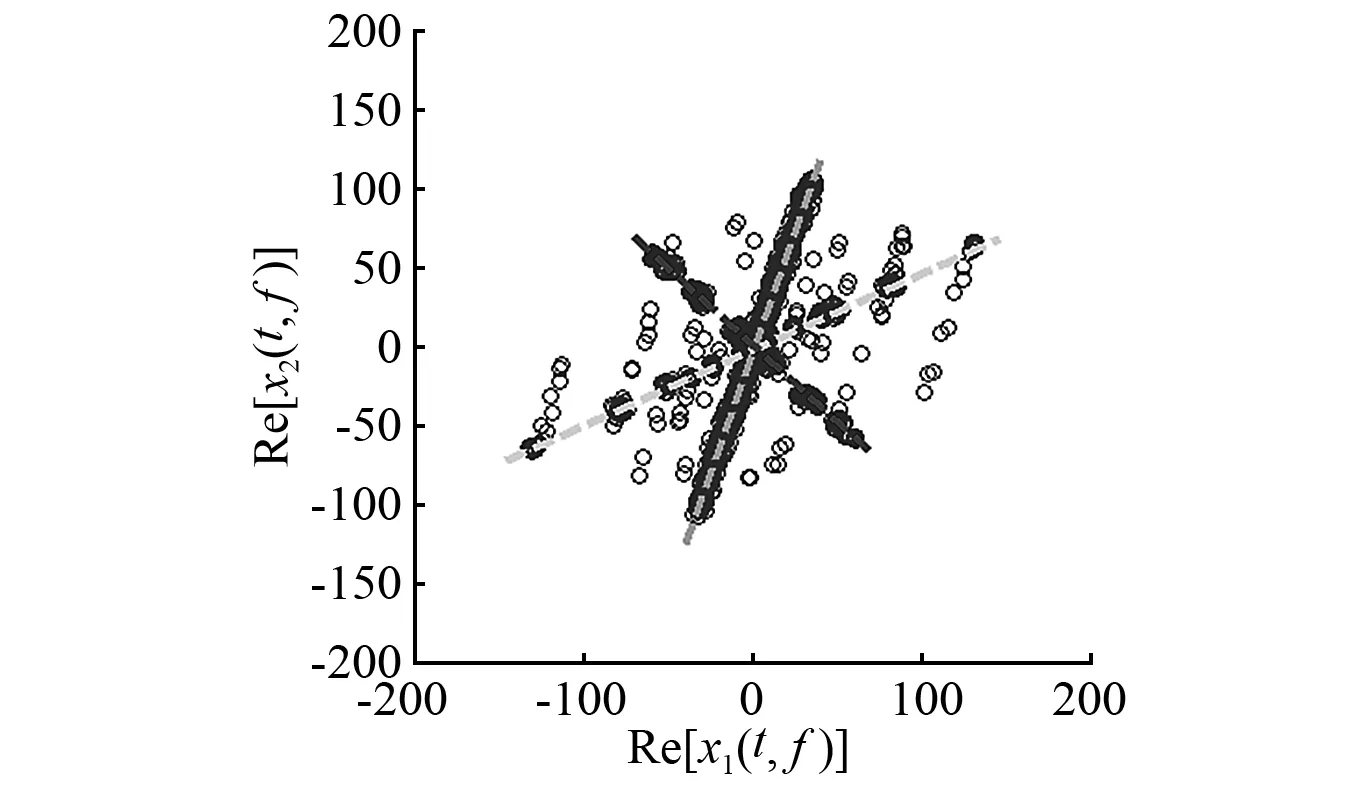
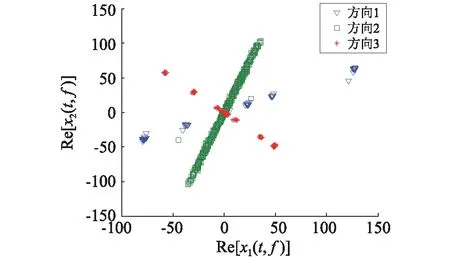
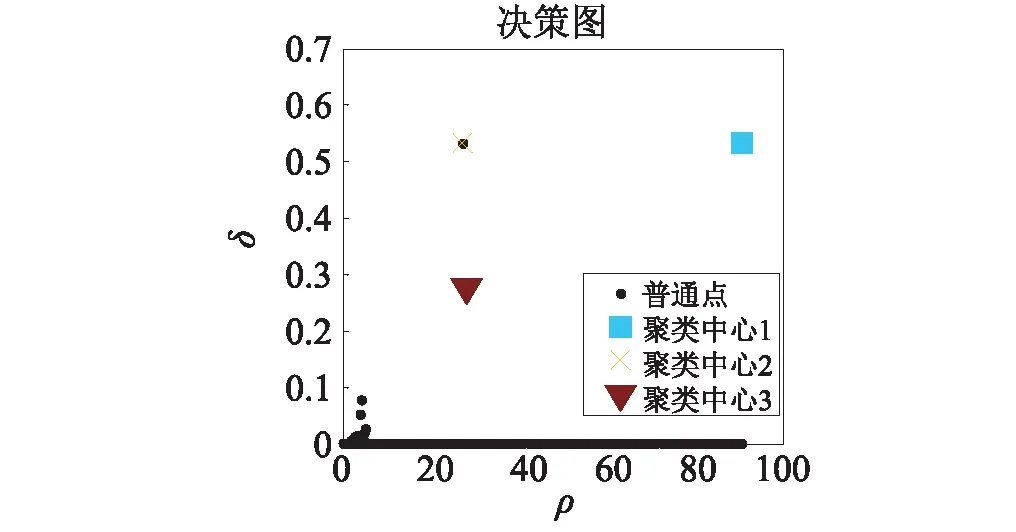
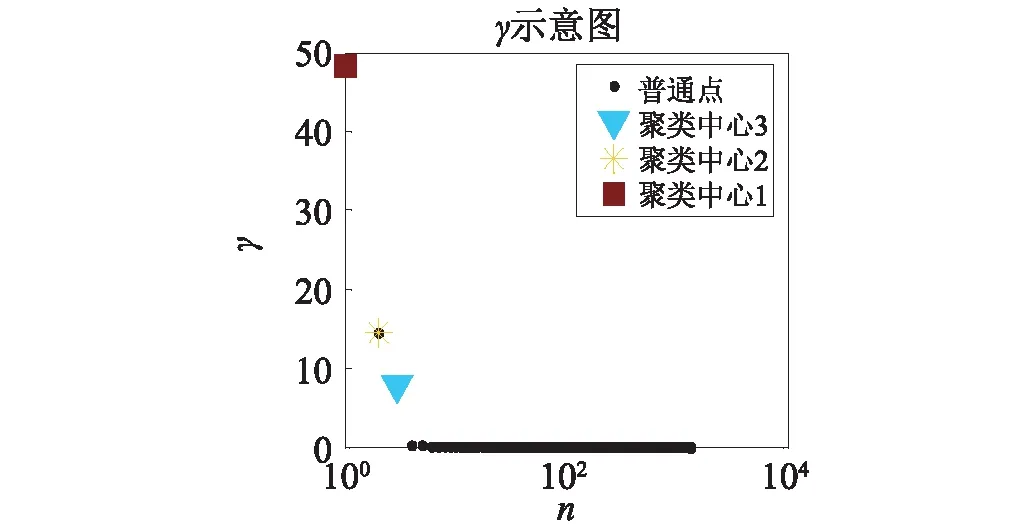
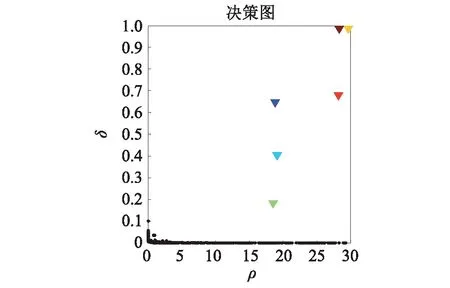
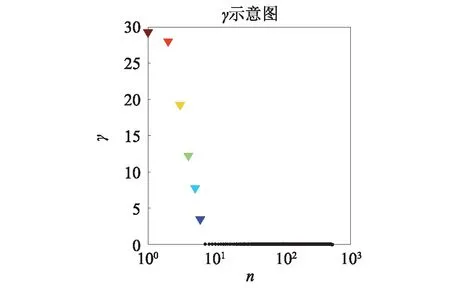
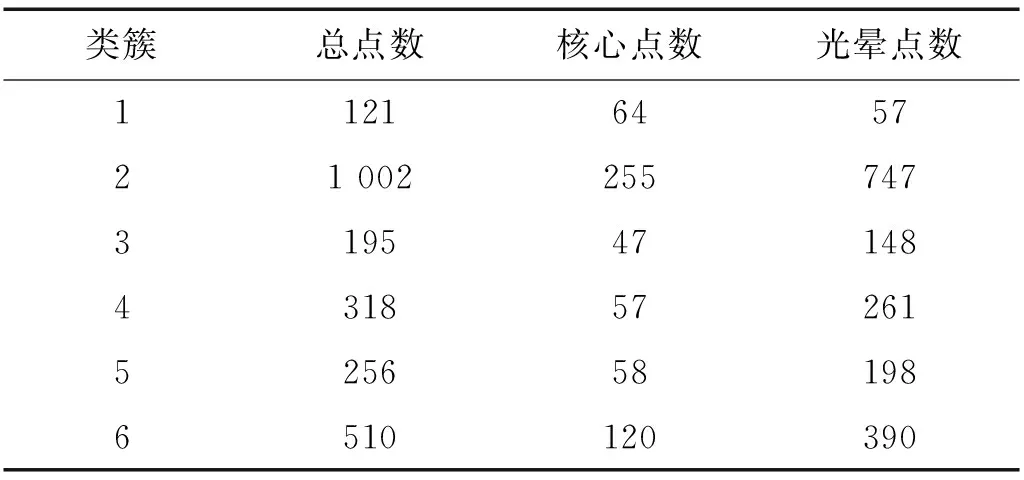
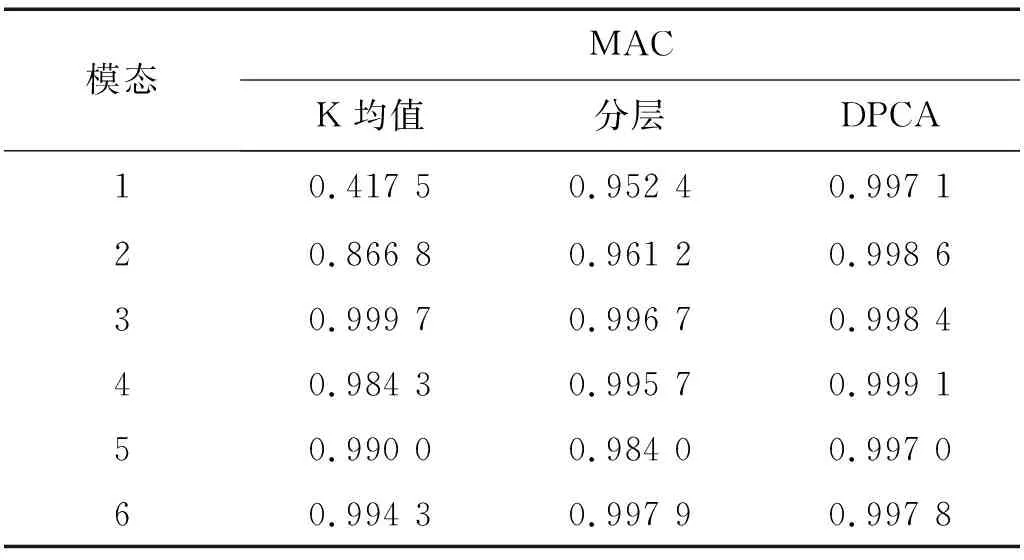
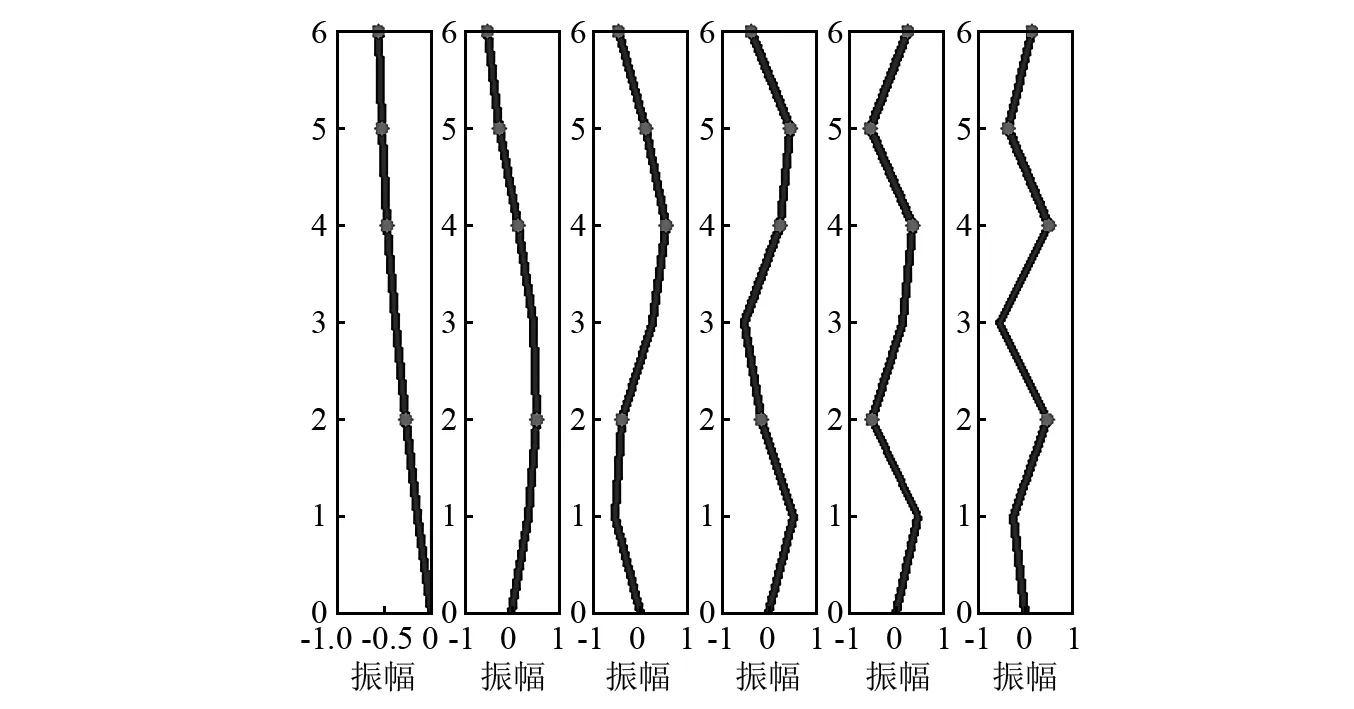
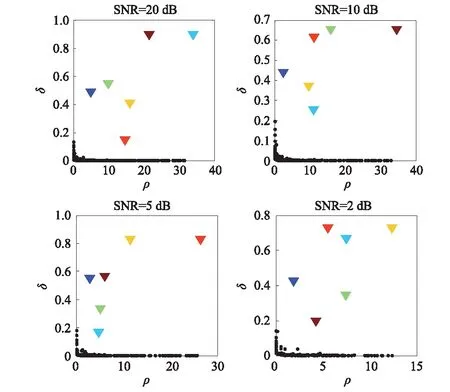
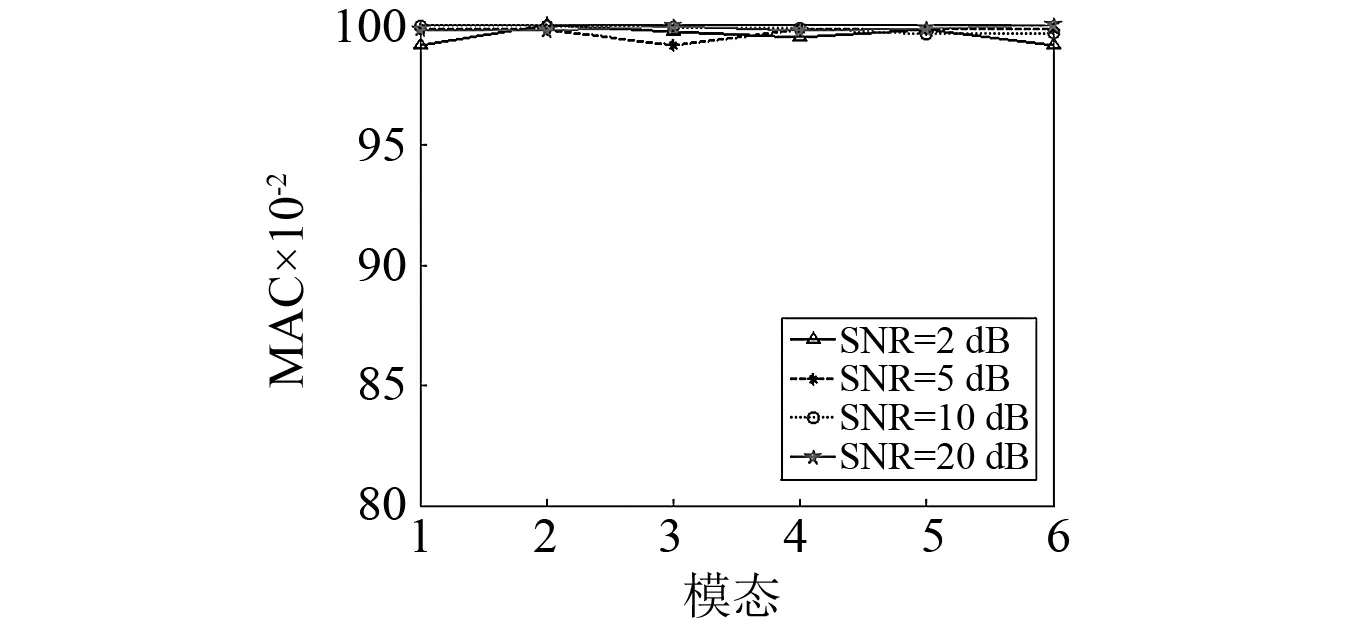
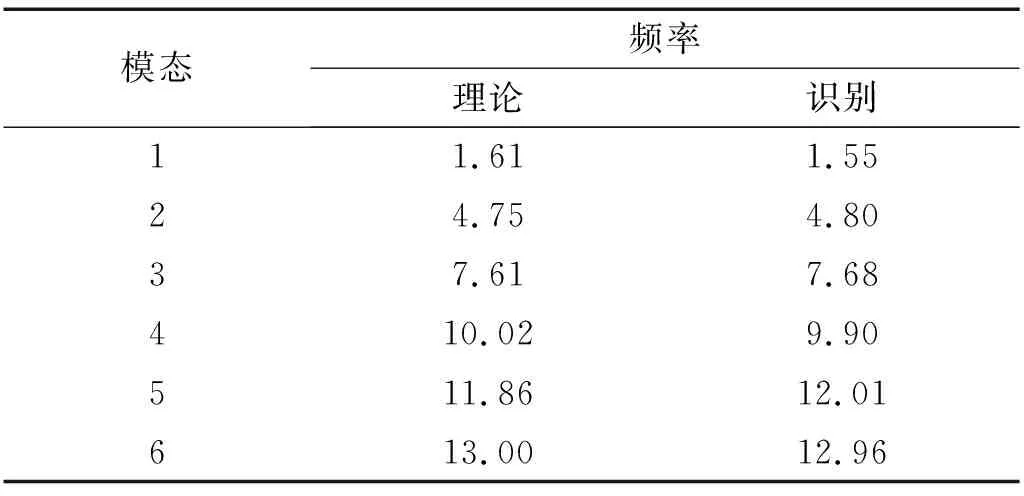
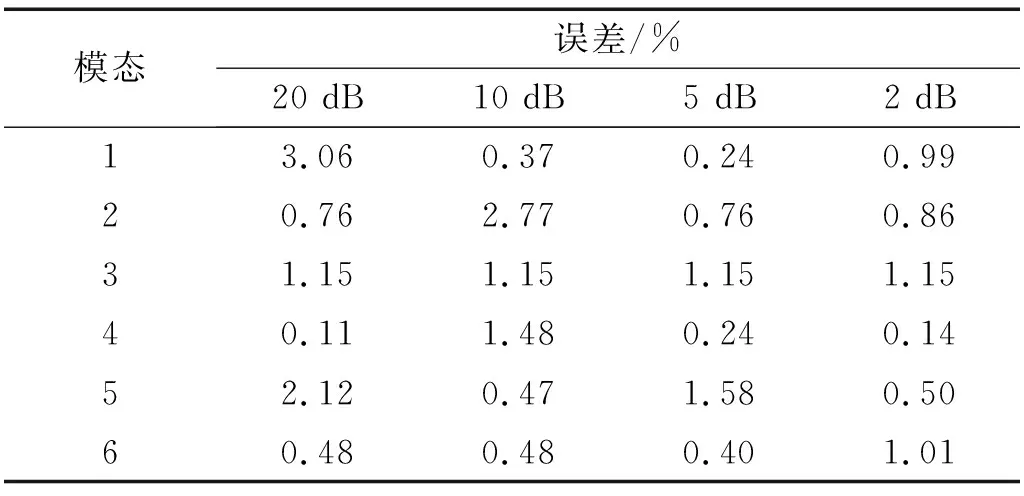
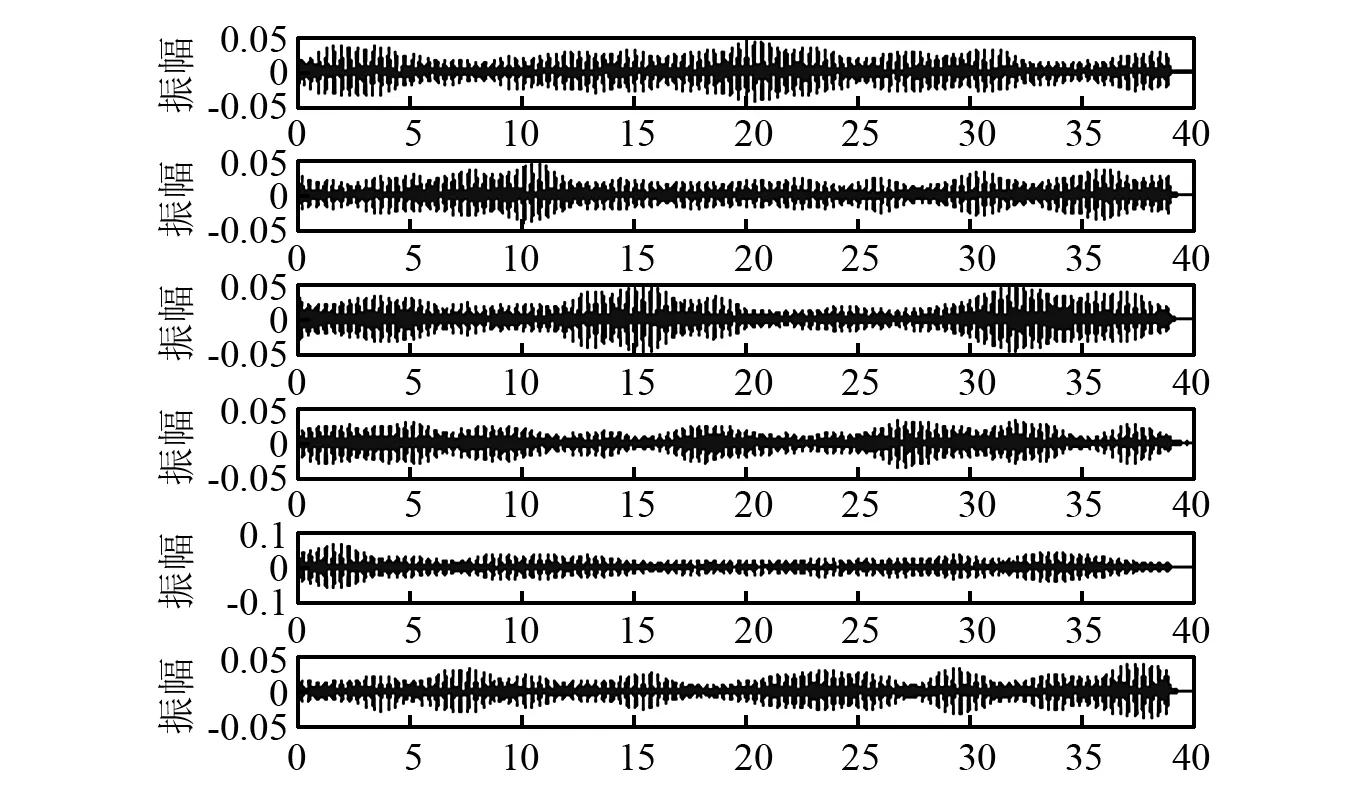
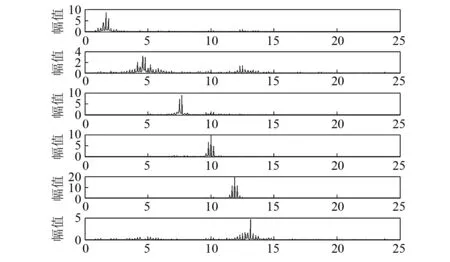
然而,文献[1-7]中的算法都只能解决BSS算法中的正定问题,即需要满足传感器数目(m)大于或等于结构自由度数目(n)。当m 本文首先利用短时傅里叶变换将信号从时域转换到时频域。针对源信号数量未知和结构高阶模态混叠的问题,利用2014年发表于science的聚类算法识别模态振型[13],它是一种基于密度峰值的聚类方法(Desity Peaks Clusering Algorithm, DPCA)。DPCA算法可以在源信号数量未知的情况下,通过决策图直观得到聚类数目,并且有效忽略频率混叠点和噪声点对聚类精度的影响。最后,利用SL0算法重构每阶模态的时频域信号,通过逆短时傅里叶变换得到单模态时域信号,进而计算出模态频率。 考查线性时不变结构系统,其在激振力作用下的微分方程为 (1) 式中:M,C,K分别为n×n阶质量,阻尼和刚度矩阵;f(t)为激振力;x(t)为位移响应。将x(t)转化到模态坐标形式为 x(t)=Φq(t) (2) 式中:Φ为模态振型矩阵,其每一列向量代表结构的某一阶振型;q(t)为模态坐标振动信号。各阶模态坐标振动信号可表示为 qi(t)=Bie-ξiωn,itsin(ωd,it+φi) (3) 式中:ωn,i和ωd,i分别为无阻尼和有阻尼的情况下每阶振型的固有频率;B和φ为两个由初始条件确定的常数;ζi为第i阶振型的阻尼比。仅通过系统的响应信号识别模态参数,即仅利用振动响应x(t)提取结构模态振型、频率和阻尼比。 上述模态参数识别问题可以与盲源分离问题对应起来。盲源分离是指在源信号与混合通道参数均未知的情况下,仅利用传感器测量信号计算各源信号的信号处理方法。BSS的数学模型为 X(t)=AS(t) (4) 式中:X(t)∈Rm为观测信号,m为观测信号数量;A∈Rm×n为未知列满秩矩阵;S(t)为未知n维源信号。对于正定问题,即m=n,盲源分离的主要任务是仅通过观测信号找到混合矩阵A并求A-1,然后由式(1)解出S(t)。 对比式(2)和式(4)可以看出,盲源分离的数学模型与模态分析时域模型有相似之处。由于源信号和混合矩阵的先验信息未知,两者都是仅通过结构系统的输出信号求解方程。模态响应q(t)相当于式(4)中的S(t),而位移响应x(t)相当于式(4)中的X(t)。本文所要解决的为欠定盲源分离问题,即m 首先利用调频信号算例说明模态振型矩阵计算原理。设混合信号由两个简谐信号和一个调频信号组成,简谐信号q1和q2频率分别为10 Hz和20 Hz,调频信号q3从5 Hz增加到15 Hz,调频信号的频率范围保证了信号在时频域有混叠成分;采样频率100 Hz;加入混合信号能量10%的白噪声。设矩阵Φ为 (5) 利用短时傅里叶变换将混合信号x(t)转换到时频域上,得到稀疏信号 x(t,f)=Φq(t,f) (6) 该混合信号的时频图如图1所示。式(6)中源信号数量为3,观测信号数量为2。式(6)亦可写作 (7) 图1 混合信号时频图Fig.1 The mixing signals in the time-frequency domain 假设存在一点(t1,f1),仅存在源信号q1,那么式(7)可以简化为式(8)和式(9) Re(x1(t1,f1))=a11Re(q1(t1,f1)) (8) Re(x2(t1,f1))=a21Re(q1(t1,f1)) (9) 式中:Re为取实部,由式(8)和式(9)可知 Re(x1(t1,f1))/Re(x2(t1,f1))=a11/a21 (10) 由式(10)可知,通过混合信号时频点实幅值的比值可得到混合矩阵第一列向量,重复这一步骤可以得到混合矩阵每一列向量。式(10)中选取虚部和实部的结果是一样的[14]。绘出两个混合信号在时频域上的实部幅值散点图,如图2所示。图中散点的排列方向趋近于Φ矩阵各列向量的方向,如图虚线所示。通过聚类算法求出每一组的聚类中心,即为振型矩阵的每一列向量。 图2 混合信号幅值散点图Fig.2 Scatter plot of the amplitude of the mixing signals 图2中,位于虚线上的点称为单源信号点,而远离虚线的点称为多源信号点。多源信号点会影响聚类算法的精度。为提高聚类算法精度与效率,宜先剔除多源信号点。当同一时频点对应的实部向量与虚部向量的夹角低于某一阈值时,可以认为该点为单源信号点[15]。实部,虚部和夹角满足下列关系式 (11) 式中:Im为虚部;θ为混合信号实部向量与虚部向量的夹角阈值,2°即可满足要求。 选取满足式(11)的时频点可以保证每个源信号互相独立,在时频域上无混叠成分。图3为去除多源信号点的混合信号幅值散点图。图中三类标记的数据点分为三个排列方向,即混合矩阵的列向量。可以看出,通过设置实部与虚部角度的阈值可以很大程度上减少计算量并且提高聚类精度。对这些时频点进行聚类可计算出模态振型矩阵,聚类方法在下一节进行介绍。 图3 去除多源点混合信号幅值散点图Fig.3 Scatter plot of the amplitude of the mixing signals after eliminating source points 本文利用一种基于峰值密度的聚类算法估计模态振型,该算法应用于模态分析的方面有两个优点:①不需预先知道结构自由度数或活跃模态数,通过决策图直观选出聚类中心和聚类数目;②可以有效地分离噪声点,从而保证模态振型计算的精度。 算法的核心思想是寻找被低密度区域分隔的高密度峰值点。对于一个数据集,聚类中心总是被低局部密度的数据点包围。DPCA主要分为2步:①通过计算每个数据点的局部密度ρi和与更高密度点之间的距离δi,确定聚类中心;②将所有数据点划分到对应的类簇中。 局部密度ρi的定义为 ρi=∑jχ(dij-dc) (12) 其中, (13) 式中:dc称为截断距离,为自定义参数。所选dc使得每个数据点的平均局部密度为数据点总数的1%~2%。本文所用距离公式为1-|cosα|,α为数据点对应的向量夹角。 对于数据点i,若存在更高密度的数据点,δi由式(14)计算 δi=min(dij),j∈Is (14) 式中:Is为所有局部密度大于数据点i的序号的集合。即,δi表示在所有局部密度大于xi的数据点中,与xi距离最小的数据点与xi之间的距离。当数据点i有最大局部密度时,Is=Ø,δi取最远数据点与xi之间的距离。 因此,每一个数据点xi有对应局部密度和距离值:(ρi,δi)。在二维图中画出每一组(ρi,δi),即为决策图。当xi同时有较大的ρ值和δ值时,则被认为是数据集的聚类中心。考虑图3中的算例,将所有数据点对应的(ρi,δi)在平面上表示出来(ρ为横轴,δ为纵轴,ρ和δ已被归一化),如图4所示。 图4 图3中数据点决策图Fig.4 The decision graph for the data inFigure 3 图4中有3个标记点“脱颖而出”,同时拥有较大的ρ值和δ值,表示源信号有3个。每一种标记类型点对应着图2中的一个排列方向。由图4可知,正方形聚类中心有最大局部密度ρ,此时式(14)中的Is为空集。因此,正方形聚类中心的δ取最远的数据点到它的距离。三角形与星形聚类中心不具有最大的局部密度,但局部密度比它们大的点属于其他类簇,因为聚类中心在该类簇中有最大的ρ值。因此,3种标记点都有较高的δ值。对于圆点,比它ρ更大且距离最近的点与其属于同一类簇,所以圆点δ值较小。 若决策图中无法直观地得到聚类数目时,可通过计算γ值确定类簇数目 γi=ρiδi,i∈Is (15) 图5 数据点γ值分布图Fig.5 The value of γ in decreasing order 考虑2.1中的算例,在确定了3个聚类中心后,再对图3中所有的圆点数据进行归类。决策图(见图4)中各聚类中心ρ值的大小关系为:三角形的密度<星形的密度<正方形密度。对比图3与图4也可发现,在正方形类簇对应的方向上,数据点聚集得最为密集,而三角形与星形点略为稀少。 得到局部振型矩阵后,式(6)变为一个欠定的线性方程组。由于源信号在时频域具有稀疏性,附加一定限制条件可以寻找最稀疏解。于是求解式(6)转化为一个最优化问题,对于时频点(t,f),求解模型为 (16) l0范数最小优化方法是求解该问题的方法之一。但是由于l0范数对噪声极为敏感,任何大于零的数都会被当作非零数。通常用l1范数代替l0范数,转化为一个凸优化问题,可以用线性规划方法进行求解,但该方法复杂度高,计算量大。因此Mohimani等通过最速下降法和梯度投影原理提出用平滑函数趋近信号的l0范数,把最优化问题转化为平滑函数的极值问题,称为平滑l0范数重构算法。它可以在保证同样精度的情况下,重构速度比基追踪算法[16]快2~3倍。 SL0的核心思想是用一个连续光滑函数去估计不连续的l0范数。此光滑函数采用均值为0的高斯函数 (17) 式中:s为复数;σ为函数的光滑程度,数值越大越函数光滑。当σ趋近零时 (18) l0范数计算向量中的非零元素,而SL0是计算向量中零元素的数量。对于有n维的任意向量s,其近似连续函数可以写成 (19) 最后l0范数最小值问题归为连续函数Fσ(s)最大值问题。 ‖s‖0≈n-Fσ(sj) (20) 对于上文所述算例,在时频点(t,f)处,观测量有两个,未知量有3个。SL0算法即是要找出一组q1(t,f),q2(t,f),q3(t,f),在满足式(6)的同时使其平滑l0范数最小(或‖s‖0最大)。 采用一个6层剪切框架模型作为算例,各层刚度和质量分别为176.729 MN/m和100 t;第一阶阻尼比为0.05;采样频率取50 Hz,采样时间取40 s;各层受白噪声激励,采用龙格-库塔法进行振动响应计算;位移传感器数量取4个,少于结构自由度数量,分别布置在2层、4层、5层、6层。对响应信号进行短时傅里叶变换。为了减小聚类计算量,先利用式(11)去除在时频域发生频率混叠的时频点,再进行后续识别。 在计算结构阵型时,选取dc使得每个数据点的平均邻居个数为数据点总数的1%。图6和图7分别为峰值聚类算法的决策图与γ值降序分布图。 图6 仿真算例决策图Fig.6 The decision graph of the simulation example 图7 仿真算例γ值分布图Fig.7 The value of γ in decreasing order for the simulation example 图6中有6个三角形点同时拥有较大的ρ值和δ值,表示数据点被分为6类簇。图7也可以看出,有6个点γ值较大。可判定聚类中心为6个。 由于环境激励和阻尼会使散点图中有很多噪声点,使高阶模态难以识别。为了区分噪声点,DPCA方法中引入了边界区域的概念。边界区域的是属于某一类簇但与属于其它类簇的数据点距离不超过dc的数据点的集合。在边界区域中,定义最大的局部密度点对应的局部密度为ρb。若类簇中数据点的密度值高于ρb,则视为核心点;剩下的则被视为类簇光晕点。将图6中三角形点作为聚类中心,得到的核心点与光晕点如表1所示。例如表1中的类簇2,属于该类簇的点数共有1 002个,其中大于边界密度的核心点有255个,小于边界密度的光晕点共有747个。取核心点平均方向作为类簇方向,可有效降低模态振型识别误差。 为表明DPCA聚类方法的优点,用模态置信准则(Modal Assurance Criterion, MAC)评估模态振型识别结果,对比了三种方法聚类识别出的振型结果,各阶振型MAC如表2所示。 由表2可知,K均值和分层聚类识别的第一阶和第二阶振型并不精确。K均值聚类初始值选取不佳可能导致算法无法收敛到最优解,且需要预先确定类簇数目;分层聚类虽然不需要输入类簇数目,但是一旦聚类被分裂或合并后,就无法返回,聚类质量受限制[17]。而DPCA聚类可以把数据点分为核心点和光晕点,光晕点中包含噪声点。在计算聚类均值时,仅采用核心点,保证了计算模态振型的精度。识别振型与理论振型的对比如图8所示,可见各阶模态振型均能被精确识别。 表1 DPCA聚类后数据点分布情况Tab.1 The distribution of the points 表2 三种聚类方法计算振型MAC值Tab.2 The MAC obtained by three clustering algorithms 图8 模态振型识别值与理论值对比Fig.8 The mode shapes of the identification value and the theoretical value 为了验证明该算法的抗噪性,对传感器信号加入白噪声。信噪比分别取20 dB,10 dB,5 dB,2 dB,不同信噪比下的DPCA决策图如图9所示。 从图9可以看出,随着传感器信号信噪比减小,决策图中处于“特殊位置”的标记点数目没有发生变化,始终是6个。将图中标记点作为聚类中心所识别的模态振型MAC值,如图10所示。 图10中各阶振型的MAC值均在0.99~1,说明该算法识别模态振型结果受噪声影响较小。且图9和图10证明了PDCA在较高噪声水平下仍可以准确选择出结构的自由度数目和识别模态振型。 图9 各种信噪比下的决策图Fig.9 The decision graph under various SNR 图10 各种信噪比下识别的模态振型Fig.10 The mode shapes MAC under various SNR 得到模态振型后,采用SL0算法重构各阶单模态信号。重构后的各阶单模态振动信号时频域能量分布如图11所示。 图11中最大能量对应的频率值由直线标出。为提高频域分辨率,可通过逆短时傅里叶变换将时频域信号转换到时域,再由快速傅里叶变换得到更精确的结果。各阶模态坐标信号如图12所示,对应傅里叶变换如图13所示。识别出的各阶模态频率见表3。由识别结果可见各阶模态频率识别精度较高。 表4给出了不同信噪比下算法识别出的模态频率包含的误差,各信噪比下模态频率识别结果较稳定,误差基本在1%左右,只有个别误差超过2%,这说明算法对噪声有较好的鲁棒性。 除上述数值算例外,利用本文算法,也精确地识别出了ASCE benchmark模型[18]的模态振型和频率,限于文章篇幅较长,未在文章中展示。 表3 频率识别值与理论值Tab.3 The mode frequency of the identification value and the theoretical value 表4 不同信噪比时的识别模态频率识别误差Tab.4 Modal frequency error under various SNRs 图11 各阶模态信号时频域三维图Fig.11 Time-frequency representation of recovered modal coordinate signals 图12 各阶模态时域信号Fig.12 Time domain represent of the recovered modal responses 图13 各阶模态频域信号Fig.13 Time frequency represent of the recovered modal responses 本文利用基于峰值密度的聚类算法识别模态振型,然后通过可以快速重构稀疏信号的SL0算法重构各阶单模态振动信号,并识别各阶模态频率。在数值算例中,DPCA算法可以从决策图和γ值分布图中直观地识别出源信号数量。在计算聚类中心时,DPCA算法将所有数据点分为核心点与光晕点,然后从核心点中得到更精确的聚类均值。 在重构信号时,充分利用了结构振动响应信号在时频域上的稀疏特性,采用SL0算法,精确高效地重构出单模态振动信号。数值算例显示,在较低信噪比下,算法仍可以准确识别结构模态振型和模态频率,对噪声有较好的鲁棒性。算法适用于传感器数量小于结构自由度数的盲源分离问题,为结构模态参数识别提供了新的选择。1 盲源分离与模态参数识别
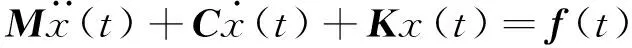
2 模态振型矩阵计算
3 DPCA算法
3.1 确定聚类中心
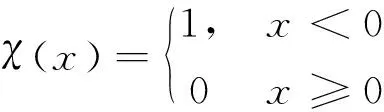
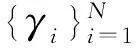
3.2 剩余数据点归类
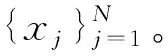
4 SL0算法基本原理
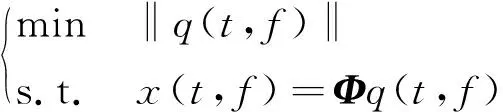
5 模态识别算例
5.1 模态振型计算
5.2 单模态信号重构

6 结 论

