一种基于关联熵融合与改进回声状态网络的故障预测方法

王浩天，段修生，单甘霖，孙 健，邱锦涛

(1.61716部队，福州 350000； 2.陆军工程大学，石家庄 050003；3.石家庄铁道大学，石家庄 050003； 4.中国洛阳电子装备试验中心，河南 洛阳 471003)

液压泵性能退化是一个相对复杂的过程，为了更好地实现故障预测，必须确定合适的退化特征[1]。为此，课题组经过前期研究，从多个层面对故障信息进行挖掘：为了挖掘信号中所包含的高阶统计信息，利用离散傅里叶变换代替传统双谱法中的傅里叶变换，提取离散傅里叶变换高阶奇异熵(The Discrete Cosine Transform high Order Singular Entropy,DHOSE)作为退化特征，以揭示性能退化的整体趋势信息[2]；为了挖掘信号中所包含的的多重分形特性信息，利用加窗法改进多重分形去趋势波动分析法(Multi-Fractal Detrended Fluctuation Analysis,MF-DFA)，通过对常用的谱参数性能进行对比分析，提取多重分形谱峰值所对应的奇异值α0和谱宽Δα作为退化特征，以揭示性能退化的内部动力学特性信息[3]；为了挖掘信号中所包含的敏感故障信息，对信号进行局部特征尺度分解，利用贝叶斯信息准则和互信息相结合，从所得的内禀分量中筛选出所需的敏感分量，经过融合后，提取复合谱熵DCSE作为退化特征，以揭示性能退化的细节敏感信息[4]。但是，过多的特征虽然保证故障信息的全面性和完整性，也会增加信息的冗余程度，还可能会出现冲突信息，造成决策误判[5]。针对此问题，文献[6-7]采用降维处理，对特征进行约简，降低了计算量，但是这种降维处理很可能会出现对特征的直接剔除，造成一些敏感特征信息的遗失，导致特征的部分重要特性的损失。因此，本文将引入信息融合的思想，采用一种关联熵的融合模式，通过对各个特征向量包含信息的综合利用，实现特征层级的融合，在尽可能提高特征简洁度的基础上，进一步改善融合特征的性能。

此外，基于数据驱动的预测方法已经得到了广泛应用，并取得了一定的效果。但是，灰色模型对于非线性、随机性较强的序列预测效果较差，且GM(1,1) GM(1,1)是基于等时距建立的，而实际采集的状态数据大都是非等间距的，限制了该方法的应用范围[8-9]；隐马尔科夫模型对于系统中含有噪声以及其它不确定性因素时的处理效果不佳，影响了预测效果[10-11]；极限学习机对于输入权值向量和隐层节点阈值的随机选择，会影响输出稳定性和预测精度[12-13]。回声状态网络(Echo State Network,ESN)[14]以储备池作为内部网络，提高了非线性状态空间的复杂性和多样性，具有非常强的非线性映射能力，显著减少了学习过程的运算量[15]。由于ESN储备池内部神经元采用随机稀疏连接方式，指导性和目的性较差，影响了网络泛化能力，且储备池的拓扑结构与内部动力学特性息息相关，有待进一步完善。

因此，本文提出一种基于关联熵融合与改进ESN的故障预测方法。首先，构建基于关联熵的特征层级融合算法，对所提取的特征信息进行综合利用，进一步改善融合特征对性能退化特征的表征能力；在此基础上，通过对ESN储备池结构和内部矩阵连接权值的改进，建立ESN预测模型，进一步提高预测精度；最后，通过对液压泵全寿命试验数据的应用分析，对本文所提出的方法有效性进行验证。

1 基于关联熵融合算法的预测特征构建

1.1 关联熵融合算法

关联熵能够有效地反映不同变量间的信息冗余程度，取值越大，两变量之间的关联关系越明显，信息冗余度越大[16]。

为了避免因过度融合[17]所造成的信息遗漏，本文选取θ=0.9×I0作为融合判据，其中I0为各特征量初始最小关联熵。由于每次融合都是选取具有最大关联熵的两个特征量，融合后的新特征量和剩余特征量的关联熵必定小于初始的关联熵，因此在进行下次融合前需要判断此时的最大关联熵与判据θ的大小关系。

关联熵融合算法的预测特征构建具体过程如下：

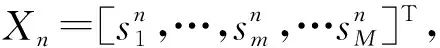
步骤1计算Xn所包含的特征信息量H(Xn)

(1)

I(Xn1,Xn2)=H(Xn1)+H(Xn2)-H(Xn1n2)

(2)

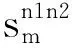
(3)

步骤3选取最大关联熵Inxny，判断Inxny与θ的大小：若Inxny>θ，则选择Inxny所对应的特征向量Xnx与Xny，将其从原特征数据集X中剔除，用二者融合后的新特征向量Xnxny代替(其计算方法同式(3))，形成新的N-1维特征数据集X；若Inxny≤θ，则跳至步骤5，输出融合后的特征向量集。

步骤4重复步骤1～3，直至特征数据集X的维数等于1。

步骤5输出结果即为预测特征向量。

关联熵融合方法并不是单纯对特征删减的降维处理，而是在保留原有特征基本信息的同时，将关联性大的两个特征融合成一个全新的特征，在提高特征简洁性的同时，尽可能改善预测特征的性能。

1.2 仿真分析

为了验证关联熵融合算法的效果，本节将利用仿真信号进行具体分析。设置采样频率fs=1 024 Hz，采样时间为t=10 s，构建仿真信号y1(t),y2(t),y3(t)

y1(t)=0.2a1(t)+0.5a2(t)+n(t)

(4)

y2(t)=0.15a1(t)+0.4a2(t)+n(t)

(5)

y3(t)+0.1a1(t)+0.3a2(t)+n(t)

(6)

通过分析可知，每个信号主要包含三个分量信号，即故障信号a1(t)、谐波干扰信号a2(t)和白噪声信号。a1(t)模拟周期性冲击信号，特征频率为f0=16 Hz，冲击函数为t2e-200tsin(2π×256t)，共振频率为256 Hz；a2(t)模拟谐波干扰分量cos(2π×40t)+cos(2π×50t)，包括40 Hz，50 Hz两个频率成分，差频为10 Hz；n(t)表示白噪声，且每个信号都加入一定程度的白噪声，使得y1(t)～y3(t)的信噪比均为-3 dB。

将其等分为10段，用来模拟性能退化的不同阶段，利用MUWDF算法[18]对每一阶段的三个信号进行融合预处理，结果分别为yfinal1～yfinal10，采用文献[2-4]所提出的方法，分别计算yfinal1～yfinal10信号的DHOSE，α0和Δα，DCSE，并对其进行归一化处理(Δα在归一化后需要进行1-Δα变换)，利用所提出的基于关联熵的方法对所提取的四个特征进行融合，得到融合特征，结果如图1所示。

图1 预测特征与各退化特征的比较Fig.1 Comparison between the prognostic feature and the degradation features

由图1可知：DHOSE能够提取反映整体退化趋势的信息，但曲线整体变化较缓，敏感度不够；α0和Δα侧重于揭示信号的不规则程度信息和局部波动信息，对整体趋势的跟随能力有限，且存在波动与反复现象；DCSE侧重于反映细节信号中的敏感信息，可能会造成一些趋势信息的遗漏，其曲线变化也存在一定的波动现象；预测特征通过对上述四个特征信息的综合利用，减少了冗余信息和矛盾信息，其曲线基本位于各特征曲线的中间位置，且随退化程度的加深呈现明显的下降趋势，对退化过程具有良好的表征效果。

为了进一步验证预测特征的有效性，改变原仿真信号中的噪声程度。为了便于对比分析，需要噪声强度变动控制在一定范围内，确保仿真信号各分量的实际意义。因此，本文选择信噪比为-2 dB，-1 dB，1 dB，2 dB及无噪声的情况进行分析，分别计算DHOSE，α0和Δα，DCSE，并进行归一化处理，利用基于关联熵的融合算法构建预测特征，将结果与-3 dB的情况绘至图2中。

图2 不同噪声背景下预测特征的变化情况Fig.2 Changes of the prognostic feature under various conditions

图2描述了不同噪声背景下预测特征的变化趋势。通过分析可知，无论是信息熵还是多重分形参数，都是对信号整体复杂性和不确定性的一种度量，显而易见，随着噪声程度的提高，信号自身成分越来越复杂，不确定性也随着提高，导致预测特征整体取值也随之上升。但是，这种对于每一条曲线而言，高组别数据的预测特征值明显比低组别数据的小，且随着组别数据的增加，曲线呈现显著的下降趋势，曲线变化率也基本呈现逐次增加的情形，这表明，噪声强度的变化对预测特征值有一定的影响，但是这种影响比较细微，各噪声背景下的预测特征曲线均能比较理想的反映性能退化过程，能够更为真实地反映液压泵的实际退化过程。

2 基于改进ESN的故障预测方法

2.1 ESN基本原理

作为ESN的核心网络，储备池中包含大量随机生成的神经元，这些单元往往具备记忆能力，以稀疏的方式相互连接[19]。ESN的拓扑结构如图3所示。

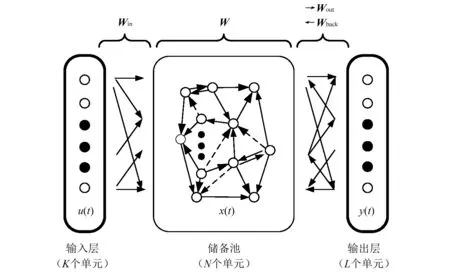
图3 ESN网络结构图Fig.3 The structure of ESN

如图3所示，u(k)为输入层输入向量，x(k)为储备池状态向量，y(k)为输出层状态向量。ESN的状态更新方程为

x(k+1)=f(Winu(k+1)+Wx(k)+Wbacky(k))

(7)

式中：f()为神经元的激励函数；x(k)和y(k)分别为第k时刻的状态向量和输出向量；u(k+1)为第k+1时刻的输入向量，Win，Wback分别为输入连接权值矩阵和反馈连接权值矩阵；W为储备池内部的连接权值矩阵。ESN的输出方程为

y(k+1)=f(Wout(u(k+1),x(k+1),y(k)))

(8)

式中：Wout为输出权值矩阵。通过状态更新方程以及输出方程，ESN能够利用储备池中的神经元激发出复杂多样的非线性空间，减少了局部极值现象的出现，提高了对非线性序列的预测能力。

2.2 ESN的改进

ESN储备池内部单元采用的是随机稀疏连接模式，这种连接模式存在指导性和目的性差的问题，使得储备池网络拓扑结构的随机性难以满足对不同特性时间序列的预测需求，影响了ESN的泛化能力以及预测精度[20-21]。

因此，需要储备池网络能够对自身结构进行动态修正。考虑到NW小世界网络[22]中，节点间的连接权值只能为0或1，导致邻接矩阵中的元素或为0或为1，属于确定性连接，致使其对自身结构的修正能力无法满足对非线性时变序列的预测需求[23]。为此，在改进ESN模型中，对NW小世界内部节点连接权值p进行了重新定义。通过分析可知，单纯依靠该距离来定义p，会导致网络内部节点连接随机性的降低。为了同时融入距离与随机性对加边的影响，改进ESN模型中p的定义式可描述为

p=e-λd+(1-e-λd)rand(0,1)

(9)

式中：d为节点间的欧式距离；λ为调整参数；p的取值范围为0～1，由距离因子e-λd和随机因子rand(0,1)共同决定：当节点距离越近时，e-λd越接近于1，1-e-λd则趋近于0，此时d为p的主要决定因素；而当节点距离越远时，e-λd越接近于0，1-e-λd则趋近于0，此时rand(0,1)为p的主要决定因素。

利用式(9)所定义的改进ESN内部连接方式，同时融入了对节点间的随机因素和距离因素的考虑，使得储备池能够根据输入序列的特点，动态改变自身拓扑结构，改善网络的泛化能力。

2.3 基于改进ESN的故障预测

为了提高预测精度，目前神经网络的预测过程多采用动态多步预测策略，即在每次预测后，仅利用一部分的输出结果对相应地预测数据进行更新，剩余预测结果则用于更新输入向量，保证预测模型的同步更新，改善模型的适应能力。因此，本文也采用动态多步预测策略，在每一步预测完成后，选取部分输出结果作为该单步预测结果，并以此对输入向量进行更新，继续后续预测，以此实现预测。其具体实现步骤为：

步骤1利用液压泵性能退化试验数据，分别提取DHOSE，α0和Δα，DCSE四个退化特征，采用基于关联熵的算法对其进行处理，得到预测特征。

步骤2根据液压泵在不同退化阶段的故障特点，选择合适的预测区间[Ta,Tb]和训练区间[Tc,Ta-1]，其中[Tc,Ta-1]作为已知数据对改进ESN进行学习训练，而[Ta,Tb]作为未知数据区间用于检验改进ESN的实际预测效果。

步骤3利用文献[24]提出的果蝇优化算法，对改进ESN的储备池规模EN以及内部连接矩阵谱半径ER两个参数进行优化：①设定参数寻优的目标函数为训练区间改进ESN输出值与真实值的均方根误差，果蝇种群规模为Nf，最大步长值为Len；②随机初始化位置坐标(x0,y0)，搜索食物位置并更新种群位置坐标

(10)

式中：k=1,2,,Nf；len为[-Len,Len]的随机值；③计算当前位置的味道浓度Smk

(11)

④搜索出味道浓度最高的果蝇，保留该果蝇的位置，判断此时的最高浓度值是否优于前一次迭代的最高值，若是，则跳至⑤，否则，重复②；⑤引导果蝇群体飞向浓度最高的位置，判断是否满足终止条件，若满足，则当前的果蝇位置即为食物的位置，跳至⑥，否则，重复②；⑥将最终得到的果蝇位置(xopt,yopt)作为参数EN，ER的最优值。

步骤4设定步进值为k，利用训练好的改进ESN，采用动态多步预测策略，进行预测。具体过程可描述为：对于预测区间[Ta,Tb]，假设输入预测特征向量为[Tz1,Tz2,,TzN]，经过改进ESN得到的输出向量为[y1,y2,,yN]，将[y1,y2,,yk]作为[Ta,Ta+1,,Ta+k-1]处的预测值，同时对模型进行更新，将下次预测的输入向量更新为[Tz1+k,Tz2+k,,y1,y2,,yk]，进行下次预测。

步骤5重复步骤4，直至预测完成后，判断预测值[y1,y2,,yk]中是否存在低于指定阈值的，如果存在，则将低于阈值的预测值所对应的时刻作为故障失效时刻，如果不存在，则判定预测方法失效。

步骤6输出[Ta,Tb]的预测值，估计RUL。

3 实验数据验证

3.1 液压泵试验数据的采集

为了获取真实可靠的数据，本文在液压泵寿命试验台进行液压泵退化试验。分别在泵端盖X,Y,Z三个方向安装传感器，如图4所示，采集并存储振动信号。采样频率为5 200 Hz，采样时间为10 s，采样间隔为23 min。所采集的信号原始数据(以长度1 s为例)如图5所示。

图4 三方向振动传感器的安装Fig.4 Installation of three-dimensional sensors

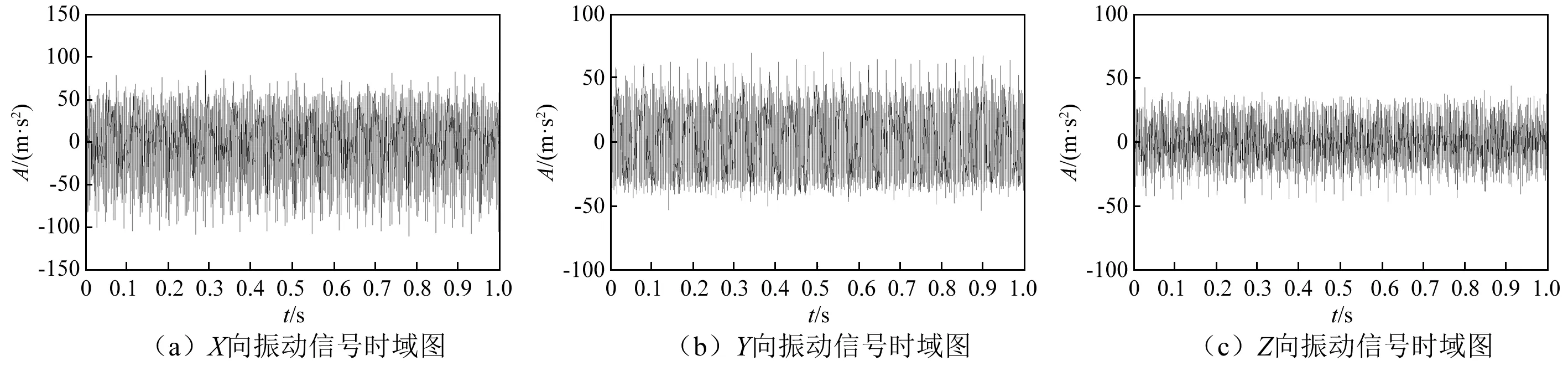
图5 X,Y,Z向振动信号时域图Fig.5 Time domain of X,Y,Z

当试验进行到37 214 min时，η=80%，系统判定泵失效，自动停机，经拆解确定为松靴故障。

3.2 实验结果与分析

(1)预测特征的构建

由于采样间隔为23 min，因此，可得到1+37 214/23=1 619组振动信号原始数据。分别利用引言中文献[2-4]的方法，计算得到的1 619组DHOSE，α0和Δα，DCSE，经过归一化处理后，利用基于关联熵的融合算法，按照1.1节的步骤1～步骤5，计算得到的预测特征如图6所示。

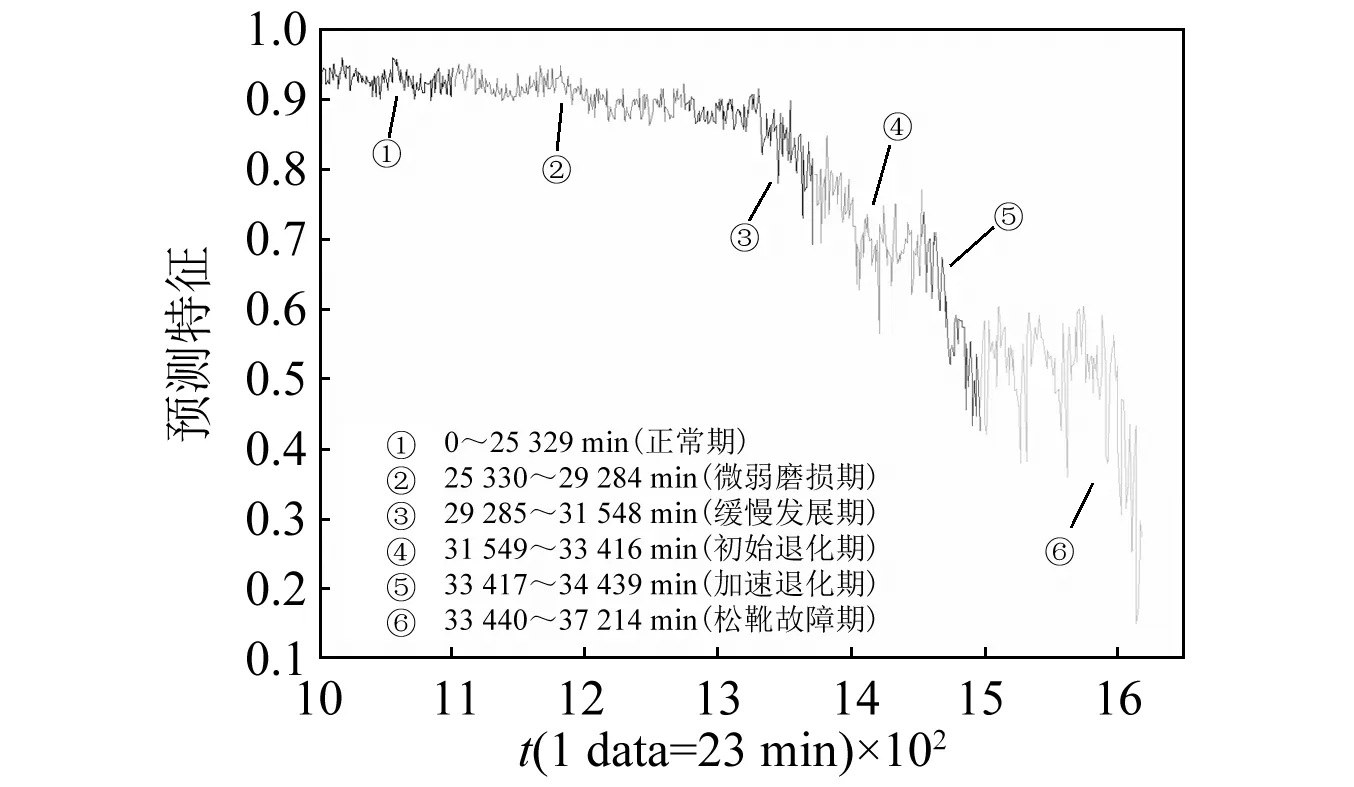
图6 预测特征在不同退化阶段的变化情况Fig.6 The changes of the prognostic feature in various stages

通过分析可知，在0～25 329 min，即第1 101组样本之前，为正常阶段；在25 330～29 284 min，即1 102～1 273组样本之间，为微弱磨损期(F1)，容积效率介于93%～95%，在这个阶段中，液压泵内部已经开始出现轻微的磨损征兆，预测特征呈现微弱下降趋势；在29 285～31 548 min，即1 274～1 372组样本之间，为缓慢发展期(F2)，容积效率介于91%～93%，在这个阶段中，摩擦副间的磨损不断加重，预测特征的下降速度开始提高；在31 549～33 416 min，即1 373～1 453组样本之间，为初始退化期(F3)，容积效率介于88%～91%，关键摩擦副间已经开始出现了故障模式的征兆，预测特征出现加速变化趋势，继而趋于较平稳的变化；在33 417～34 439 min，即1 454～1 497组样本之间，为加速退化期(F4)，容积效率介于86%～88%，油膜逐渐变薄，配合间隙增加，造成液压油的外泄，性能参数变化加剧，预测特征再次出现加速下降的趋势，并伴随一定程度的震荡，逐渐达到失效状态；在34 440～37 214 min，即1 498～1 619组样本之间，为松靴失效期(F5)，此时容积效率已经低于86%，泵已经处于完全失效状态。

考虑到在F3阶段和F4阶段，液压泵处于初始退化期和加速退化期，性能参数尚处于所要求的范围内，且预测特征的变化比较显著，能够清晰地反映故障退化规律，具有实际预测意义。因此，本文选取F3阶段作为训练区间，选取F4阶段作为预测区间，如图7所示。

图7 分析区间Fig.7 The analyzing parts

(2)预测结果分析

预测起始点设置为第1 454组数据，失效点为第1 497组数据，失效阈值设定为第1 497组预测特征的数值0.426 1。ESN网络初始输入为第1 374～1 413组预测特征值，输入输出的维数均为40。按照步骤3中的FOA算法对参数进行优化，结果为EN=30，ER=0.5。在为EN=30，ER=0.5的条件下，采用动态多步预测策略，对预测区间进行预测，为设定步进值为1，输入输出维数不变，共进行43步预测后，预测值满足失效阈值条件，停止预测，输出结果，如图8所示，预测值与实际值的误差如图9所示。

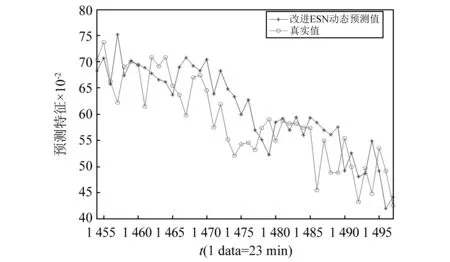
图8 改进ESN预测结果Fig.8 The prognostic results of the modified ESN

图9 预测误差曲线Fig.9 The prognostic errors

图8显示了本文所提出的改进ESN预测结果，预测值与真实值比较接近，能够较好地跟随真实值的变化过程，在第1 496组样本处，预测值小于失效阈值，判定为失效时刻，与实际失效时刻间的误差仅为1个时间点，即23 min，因此，以1 454为起点预测出的RUL=42×23=966 min。图9描述了预测曲线各点的预测误差，可以发现，最大的误差也仅在0.1左右，表明改进ESN对实际退化过程具有比较理想的预测效果。

为了作进一步对比分析，采用相同的训练与预测区间，分别利用改进ESN静态预测法、传统ESN动态预测法、NW-ESN动态预测法以及ELM动态预测法进行预测，结果分别如图10～图13所示。

图10 改进ESN静态预测结果Fig.10 Results of the modified ESN with static prognostic

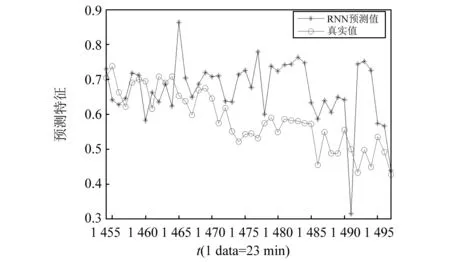
图11 传统ESN预测结果Fig.11 Results of traditional ESN prognostic

图10采用的是静态改进ESN预测方法，即每次预测后并不对输入向量进行动态更新，预测结果与实际值偏差较大，预测效果远远不如动态预测算法，无法有效地实现故障预测；图11描述了传统ESN网络的预测结果，基本能够反映变化趋势，但是预测结果与实际值间存在较大的误差，且在第1 491组样本时即满足了阈值条件，预测误差为6个时间点，即138 min，这主要是由ESN固有缺陷所导致的。

图12 NW-ESN预测效果Fig.12 Results of NW-ESN prognostic

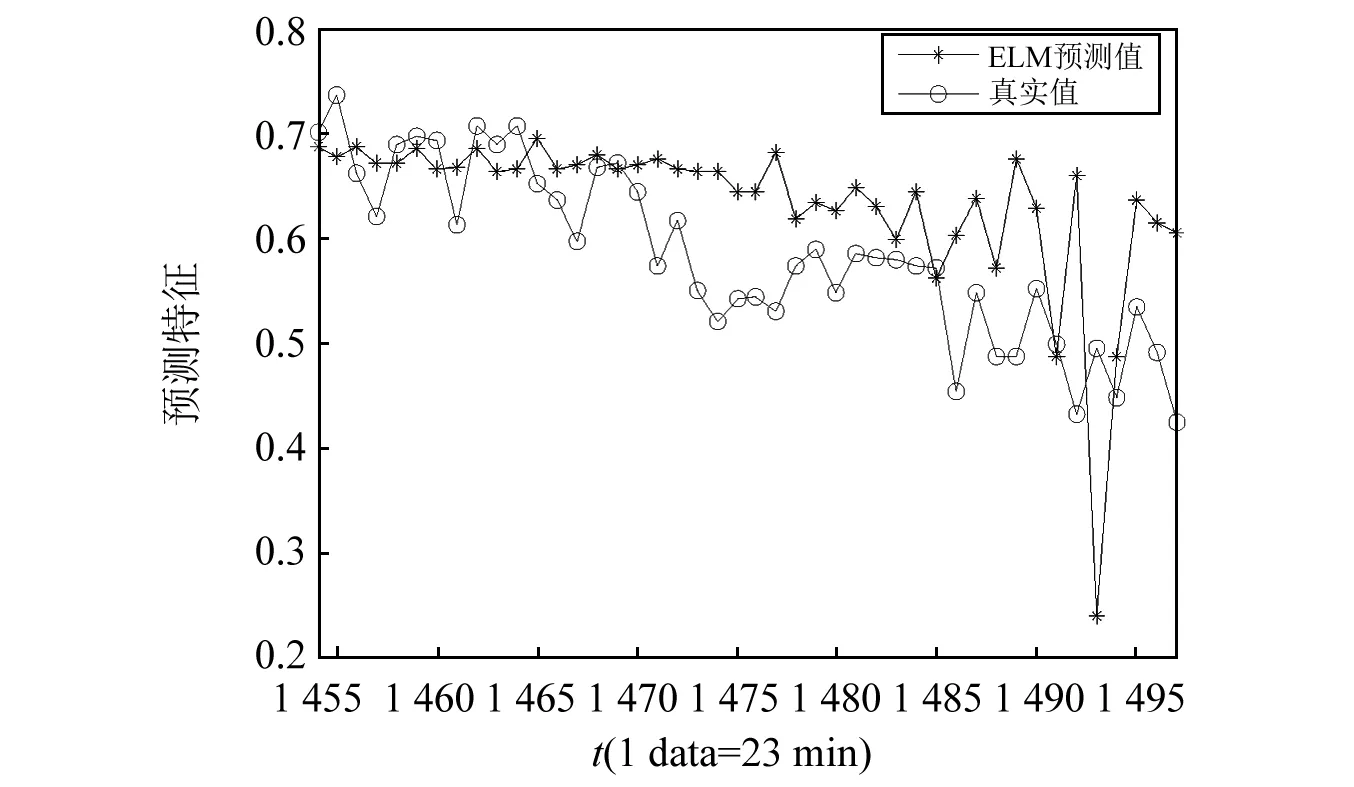
图13 ELM预测效果Fig.13 Results of ELM prognostic

图12描述了NW-ESN的预测结果，与传统ESN相比，由于采用NW小世界网络作为ESN储备池的拓扑结构，降低了部分预测误差，但是，由于NW小世界中内部节点连接值为确定性的0或1，导致对自身结构的修正能力不足，与图8所示的改进ESN的预测结果相比，预测误差仍比较大，且在第1 493组样本处即满足了阈值条件，误差为4个时间点，即92 min；图13描述了ELM的预测结果，它摒弃了梯度下降的迭代调整策略，学习速度快，但是，由于ELM输入权值向量和隐层节点阈值的随机选择，导致在第1 493组样本即满足了阈值条件，误差同样为4个时间点，即92 min。

在上述定性分析的基础上，以平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)和均方根百分比误差(Root Mean Square Percentage Error, RMSPE)作为评价指标，其计算公式分别为

(12)

(13)

分别对改进ESN动态预测方法、改进ESN静态预测方法、传统ESN动态预测法、NW-ESN动态预测法以及ELM动态预测法的预测效果进行定量评价，结果见表1。

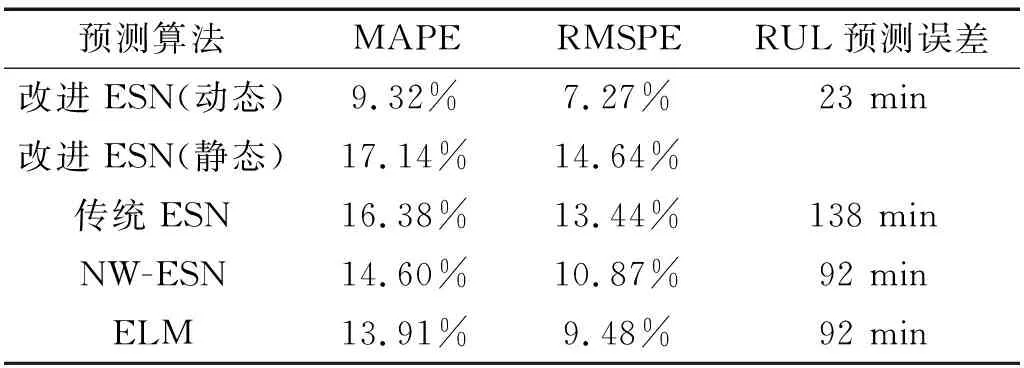
表1 不同算法的预测效果评价Tab.1 Evaluation for prognostics based upon various algorithms

通过分析表1可以发现，一方面，由于对输入向量进行实时更新，动态预测策略的预测效果要远好于静态预测策略；另一方面，本文所提出的改进ESN动态预测算法，优化了ESN的储备池结构，并利用节点间的距离以及随机因素重新定义了邻接矩阵中各元素的值，解决了ESN网络的指导性、目的性差的问题，改善了网络自身结构的修正能力，提高了网络的泛化能力以及预测精度，其MAPE和RMSPE指标均优于其它算法，且剩余寿命预测时间误差仅为23 min，具有一定的实际应用价值。

4 结 论

本文提出了一种基于关联熵融合与改进ESN的故障预测方法，并对液压泵性能退化试验所采集的全寿命数据进行了应用分析，主要结论如下：

(1)提出的关联熵算法实现了对特征信息的综合利用，有效地提高了退化特征简洁度，进一步改善了特征性能。

(2)建立的改进ESN预测模型解决了因稀疏随机连接所带来的指导性和目的性差的问题，改善了网络泛化能力与预测性能，提高了预测精度。

(3)通过对液压泵全寿命试验数据的应用分析表明，本文所提出的方法能够有效地实现液压泵故障预测，而且具有较高的预测精度。