超高速撞击充气压力容器前壁穿孔试验及预报
盖芳芳,闫龙海,高国付,于月民,唐玉玲
(1.黑龙江科技大学 理学院,哈尔滨 150022; 2.天津科技大学 机械工程学院,天津 300222)
地球近地轨道的空间碎片严重威胁着人类在轨航天器的安全运行。压力容器是航天器的关键部件之一,空间碎片的超高速撞击可能导致压力容器产生穿孔或撕裂,轻则容器发生泄漏,影响航天器的正常运行,重则航天任务可能提前终止[1]。关于压力容器的超高速撞击损伤研究,国内外研究者主要以试验和数值仿真手段为主,并且试验数据较少,定性研究多于定量研究[2-4]。鉴于超高速撞击问题的复杂性,关于压力容器损伤的预测,大部分为基于试验和数值仿真结果的经验公式,理论研究结果并不多见[5-8]。本文针对球形弹丸超高速撞击充气压力容器问题,采用试验与理论分析手段对压力容器前壁穿孔特性进行研究。研究内容分为两个方面:一方面,基于二级轻气炮进行超高速撞击试验;另一方面,基于试验结果,对压力容器前壁穿孔进行预报。
1 超高速撞击试验
1.1 试验方法
为了研究超高撞击过程中充气压力容器前壁损伤情况,利用哈尔滨工业大学高速撞击研究中心二级轻气炮进行了超高速撞击压力容器试验,共进行了20组撞击试验,试验示意图如图1所示。
试验中压力容器材料为Al6061,形状为圆柱形,直径100 mm,壁厚1.5 mm,内充氮气;弹丸材料为Al2017,形状为球形,直径均为6.35 mm。试验时弹丸正撞击压力容器前壁,弹丸撞击速度为1.5~4.1 km/s,容器内充气体压力为0.2~1.4 MPa。具体试验方案见表1(其中:dp为弹丸直径;vp为弹丸撞击速度;p0为容器内压)。

图1 超高速撞击压力容器试验示意图Fig.1 Schematic diagram of the experiments of hypervelocity impact on pressure vessels
1.2 试验结果分析
压力容器前壁损伤试验结果,如图2所示。由图2可知,全部20个撞击试验中,除了试验b9号由于弹丸在撞击容器前壁前发生破碎导致试验失败外,其他19个

图2 压力容器前壁穿孔试验结果Fig.2 Experimental result of perforation of the front wall
试验中,压力容器前壁均只产生一个较规则的圆形穿孔,无撕裂及其他损伤,并且未见明显的裂纹及翻边,将测量得到的容器前壁穿孔直径列于表1中。下面根据表1中压力容器前壁的穿孔直径试验结果,针对容器内压、弹丸撞击速度对穿孔直径的影响进行分析。
选取了2.1 km/s,2.6 km/s和3.8 km/s 3个不同撞击速度,共12组试验对容器内压的影响进行了分析。当弹丸速度为2.1 km/s左右时,选取了b3号、b4号、b5号和b2号试验工况,内压分别为0.2 MPa,0.6 MPa,0.8 MPa和1.0 MPa;当弹丸速度为2.6 km/s左右时,选取了a1号、a6号、b6号和a3号试验工况,容器内压分别为0.6 MPa,1.0 MPa,1.3 MPa和1.4 MPa;当弹丸速度为3.8 km/s左右时,选取了b8号、b11号、b10号和a9号试验工况,容器内压分别为0.6 MPa,1.0 MPa,1.3 MPa和1.4 MPa。前壁穿孔直径随容器内压的变化曲线,如图3所示。

表1 试验方案及穿孔直径试验结果Tab.1 Experimental plan and experimental result of perforation diameter
由图3可见,图中3条曲线均近似平行于坐标横轴。当撞击速度为2.1 km/s左右时,容器前壁穿孔直径为9.0 mm左右;当撞击速度为2.6 km/s左右时,容器前壁穿孔直径为10.0 mm左右;当撞击速度为3.8 km/s左右时,容器前壁穿孔直径为11.0 mm左右。可见,当弹丸直径及撞击速度相同时,随着容器内压的增大,容器前壁穿孔直径变化不大,也就是说,容器内压对容器前壁穿孔直径影响不大。由图3还可以看出,当撞击速度不同时,压力容器前壁的穿孔直径有较为明显的变化。
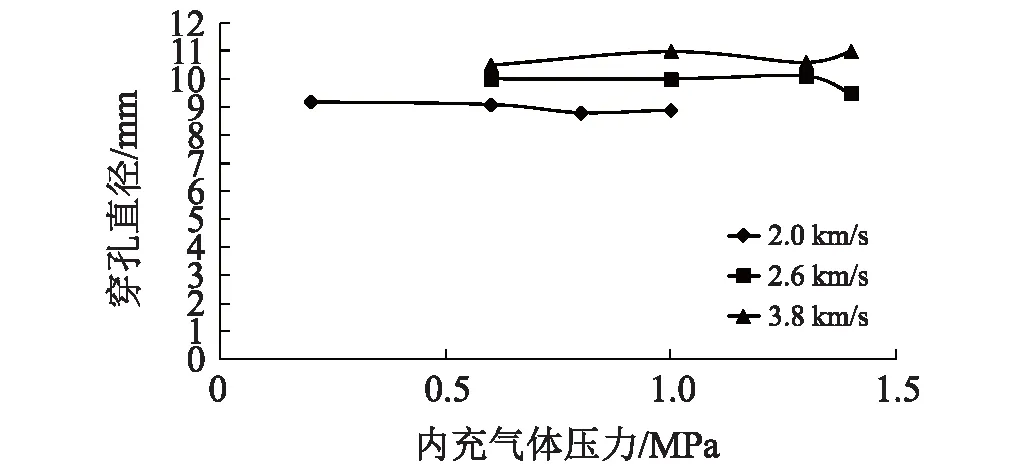
图3 穿孔直径随容器内压的变化曲线Fig.3 The change curve of perforation diameter with internal pressure
为了考察弹丸撞击速度对容器前壁穿孔直径的影响,在弹丸直径与容器内压均相同的情况下,选取b1号、b2号、a6号、a2号、a8号、b11号、a5号、a7号共8组试验工况进行分析,容器穿孔直径随着弹丸撞击速度的变化曲线,如图4所示。其中弹丸直径均为6.35 mm、容器内压均为1.0 MPa,弹丸撞击速度为1.5~4.1 km/s。由图4可见,压力容器前壁穿孔直径随着弹丸撞击速度的增大而增大,并且近似呈线性关系。由以上分析可以看出,弹丸撞击速度对容器前壁损伤影响较大。

图4 穿孔直径随弹丸撞击速度的变化曲线Fig.4 The change curve of perforation diameter with impact velocity
2 压力容器前壁穿孔预报
2.1 预报模型建立
基于试验结果分析可知,容器内压对容器前壁穿孔直径影响不大,因此对容器前壁穿孔进行建模时,可以忽略气体压力的影响;另一方面,由于穿孔直径与容器尺寸相比很小,则在分析过程中也可以忽略容器曲率的影响。因此,在弹丸撞击速度不是很高的条件下,为了简化计算,做如下假设:
(1)弹丸及容器材料在撞击过程中未发生相变,仍为固体;
(2)忽略撞击过程中摩擦、热传递等能量损失;
(3)撞击产生的碎片云没有反溅碎片;
(4)忽略容器壁曲率和内压的影响。
下面基于上述假设,建立压力容器前壁穿孔的预报模型。
由撞击试验可以发现,球形弹丸以一定速度撞击容器前壁后,不仅造成容器前壁产生穿孔,而且还在容器内形成了碎片云,如图1所示。因此,弹丸的撞击能量E在撞击过程中可以分为两个部分:一部分能量提供给弹丸撞击容器前壁形成穿孔,该部分能量用E0表示;另一部分能量提供给弹丸击穿容器前壁后形成的碎片云,即碎片云具有的动能,该部分能量用E1表示。
弹丸具有的撞击能量E可表示为
(1)
式中:mp为弹丸质量,kg。
为了计算碎片云动能E1,需要确定碎片云的质量及碎片云的速度。设在撞击过程中无材料损失,则碎片云具有的质量等于弹丸质量mp与被弹丸冲塞的容器材料质量mv之和。假设弹丸初始冲塞的穿孔直径等于弹丸直径,则mv可通过式(2)进行计算得到
(2)
式中:ρv为容器材料密度,kg·m3;tv为容器壁厚,m。
根据文献[9]的研究结果,当容器壁厚为1.5 mm、弹丸直径为6.35 mm、撞击速度不高于4.1 km/s时,弹丸在撞击过程中包括未破碎和破碎两种模式,如图5所示。在弹丸不同的破碎模式下,碎片云的速度特性是不同的,因此,下面分别针对弹丸未破碎及破碎两种模式确定碎片云的速度特性。

图5 弹丸不同破碎模式下的碎片云速度Fig.5 Debris cloud velocity of different fragmentation patterns of projectiles
当弹丸未发生破碎时,碎片云只包含一个大的碎片,该碎片由撞击压扁的弹丸和被冲塞的容器材料构成,如图5所示。考虑在撞击过程中动量守恒[10],则该碎片的速度vc可表示为
(3)
当弹丸发生破碎、并且撞击速度不高于4.1 km/s时,由文献[11]可知,碎片云的大部分质量集中在碎片云的中心元素中,其他小碎片较少。因此,可以假设碎片云所有的质量均集中在碎片云的中心元素中,并且碎片云的速度等于中心元素在撞击轴方向上的轴向速度。为了方便,当弹丸破碎时,碎片云的速度同样用vc表示(如图5所示),vc可由迟润强的研究计算得到
(4)
式中:cp为弹丸材料声速,m/s;vppf为弹丸主体材料临界破碎撞击速度,m/s,该值可根据迟润强的研究确定。
根据以上分析可见,碎片云具有的动能E1可通过式(5)计算得到
(5)
根据能量无损失的假设,弹丸撞击动能中提供给容器前壁穿孔的能量E0为
E0=E-E1
(6)
基于文献[12]对容器后壁损伤分析的建模方法,对容器前壁穿孔进行建模。将容器前壁考虑为一个厚度等于容器壁厚tv、半径为R的固支圆板,弹丸考虑为作用在圆板中心的均布冲击载荷,冲击载荷的撞击能量等于E0,作用直径等于弹丸直径dp,并且dp≪R。在均布冲击载荷作用下,容器前壁获得的初速度V和容器材料在单位面积上获得的冲量I可由式(7)计算得到
(7)
容器前壁产生穿孔的过程可分为两个阶段:初始冲塞穿孔阶段及扩孔阶段。根据最大塑性应变破坏准则,即在均布冲击载荷作用下,容器前壁产生的最大径向应变εmax达到容器材料的极限应变εf时,材料断裂产生初始冲塞穿孔,设初始冲塞穿孔直径等于均布冲击载荷的作用直径,即等于弹丸直径dp。其中,最大径向应变εmax可根据文献[13]表示为
(8)
将式(8)代入最大塑性应变破坏准则,即εmax=εf中,可以得到材料发生破坏时容器壁上的临界冲量,即
(9)
再结合式(7),容易得到初始冲塞穿孔的临界速度Vcr及产生初始冲塞穿孔所需要的能量Ecr
(10)
式中:σs为容器材料的屈服应力,Pa。
冲击载荷的撞击能量使容器前壁发生初始冲塞穿孔后,剩余能量对初始冲塞穿孔进行扩孔,直到消耗所有能量,容器前壁最终的穿孔直径Dh可由式(11)和式(12)求得。
(11)
(12)
将式(12)代入式(11)中,消去r′,并对式(11)中等号右侧第二项进行积分,最终将式(11)改写成仅关于穿孔直径Dh的公式,并通过该式计算得到穿孔直径Dh。
2.2 预报模型试验验证
将压力容器前壁穿孔直径试验结果与预报模型计算结果进行比较,如表2所示。
经过比较发现,除了失败试验b9号外,压力容器前壁穿孔直径的预报结果与试验结果的最大误差为12.2%,可见预报结果与试验结果吻合较好。并且由表2还可以发现,预报结果均小于试验结果。导致这种结果的原因主要是因为在建模过程中,忽略了撞击过程中的动量及能量损失,尤其是在弹丸破损模式下,假设整个碎片云的速度等于中心元素撞击轴方向的轴向速度,实际上碎片云中心元素上不同位置的速度是不同的,并且撞击轴方向的轴向速度最大。因此,基于上述假设计算得到的碎片云动能偏大,而提供给容器壁穿孔的能量偏小,计算得到的穿孔直径也偏小。由以上分析可见,虽然预报结果比试验结果偏小,但根据误差的分析可以看出,所建立的压力容器前壁穿孔预报模型仍是有效的。
预报模型是基于试验结果建立的,具有一定的适用范围,比如撞击速度低于4.1 km/s,容器内压低于1.4 MPa。若弹丸撞击能量或容器内压较大时,容器前壁损伤模式不仅是单一的圆形穿孔,可能产生裂纹或发生撕裂,因此容器前壁发生灾难性破坏的临界条件需要进一步研究;另一方面,在建模过程中,假设所有材料在撞击过程中未发生相变。实际上,在超高速撞击过程中,固体材料将产生液化或气化现象,但考虑弹丸撞击速度较低,忽略了撞击过程中的相变现象。由试验结果与预报结果的比较发现,这种假设是可行的,但当弹丸撞击速度超过4.1 km/s甚至具有更高的速度时,预报模型是否适用有待于进一步验证与改进。尽管如此,其研究结果对航天器类部件的防护设计仍具有一定的参考价值。
3 结 论
采用试验与理论分析相结合的手段,对球形弹丸超高速撞击压力容器前壁穿孔特性进行了研究。主要可以得到以下几点结论:
(1)基于超高速撞击试验获得了容器前壁穿孔特性及尺寸。
(2)穿孔直径随着弹丸撞击速度的增大而增大,并近似呈线性关系。
(3)容器内压对穿孔直径影响不大。
(4)建立了压力容器前壁穿孔预报模型,并验证了有效性。
由于试验条件限制,所有的撞击试验中只有一种直径的弹丸,弹丸尺寸较单一,因此,应需针对具有不同直径的弹丸对容器前壁的损伤进行进一步研究。

