核岛结构PCS水箱FSI效应简化方法研究
李小军, 宋辰宁, 周国良, 魏 超
(1. 北京工业大学 建筑工程学院,北京 100124;2.中国地震局地球物理研究所,北京 100081;3. 山东建筑大学 土木工程学院, 济南 250101; 4. 环境保护部核与辐射安全中心,北京 100082)
AP1000是美国西屋公司设计研发的第三代先进压水堆核电厂,如图1所示,核岛结构主要由屏蔽厂房,辅助厂房和钢安全壳组成。屏蔽厂房顶部的冷却水箱是非能动安全壳冷却系统(Passive Containment Cooling System, PCS)的重要组成部分,液体和屏蔽厂房之间的流固耦合(Fluid-Structure Interaction, FSI)效应会对结构的动力特性和地震反应造成影响。由于FSI效应的复杂性,常用有限元软件(ABAQUS,ANSYS,ADINA等)在求解该问题时,通常需要花费较长时间。因此,在对核岛结构进行动力分析(地震、爆炸、撞击等)时,有必要对液体晃动进行一定的简化,在满足计算要求的前提下,提高计算效率。
以地震反应分析为例,针对储液结构的经典理论,最早是Housner[1-2]针对规则储液罐,基于液体无旋、无黏、不可压缩及刚性罐壁、线弹性等假定提出的近似计算方法。核心理论是将液体动力效应分为两部分,一部分是脉冲压力,另一部分是对流压力,使得流固耦合求解过程得到简化。在此基础上,Haroun等[3-4]针对柔性结构,考虑储液罐变形的影响,提出Haroun-Housner模型,进一步将液体脉冲压力分为柔性脉冲分量和刚性脉冲分量,该简化模型更适用于工程结构,被相关抗震设计规范和标准广泛采用。
Housner模型和Haroun-Housner模型是针对规则储液结构地震分析的两种常用的简化方法,对于不规则形状储液结构的简化研究,大多集中在环形水箱[5]和纯锥形水箱[6],核岛结构中涉及的PCS水箱为底部锥形的环形圆柱结构,对于该特殊的储液结构并没有给出相关的简化计算方法。本文基于现有简化方法,针对PCS水箱,提出一种适用于核岛结构三向地震反应分析的简化模型,并与FSI模型计算结果进行对比,验证简化模型的合理性。

图1 AP1000核电厂示意图Fig.1 Diagram of AP1000 nuclear power plant
1 理论分析
考虑核岛主体结构和PCS水箱的几何尺寸和结构特性,可将其视为刚性储液结构,满足Housner模型的基本适用条件。因此,本文基于Housner模型的基本假定,开展简化计算模型研究,以提出工程分析计算精度的模拟PCS水箱液固耦合作用的简化模型。
1.1 Housner模型
1957年,Housner基于如下假定提出简化模型:①储液结构截面规则;②底部为平底;③适用于水平地震作用;④刚性结构。其核心思想是将刚性储液结构中液体晃动等效为“质量-弹簧”模型,如图2所示。图2中:m0为脉冲质量;m1为一阶对流质量;mn为n阶对流质量;k1为一阶等效弹簧刚度;kn为n阶等效弹簧刚度;h0为脉冲质量高度;h1为一阶对流质量高度;hn为n阶对流质量高度。脉冲质量附着在结构内壁,随结构作同步运动,对流质量依靠弹簧与箱壁相连,等效模拟液体晃动效应。
在具体计算和应用时,首先要确定脉冲质量和对流质量的比例关系以及其质心相对于底面的高度,然后通过计算得到液体的晃动特性以及液体晃动产生的基底剪力和储液结构箱壁的倾覆弯矩。该模型简洁实用,至今仍为国内外学者采用。

图2 Housner模型Fig.2 Housner model
1.2 简化模型
一般的储液结构(如LNG储罐、石油储罐等)底部为平底,在采用Housner模型进行简化计算时基于基本假定,通常只考虑水平地震作用。核岛PCS水箱为底部锥形的环形圆柱结构,且相关规范条例要求必须进行三向地震反应分析,而Housner模型中并没考虑液体竖向振动。
考虑PCS水箱的特殊结构形式和需要进行三向地震反应分析要求,本文参考Housner模型的计算方法,分两步推导建立PCS水箱简化模型:①计算脉冲质量和对流质量的比例关系、对流质量质心相对于底面的高度;②计算液体的晃动频率,根据晃动频率和阻尼比确定连接对流质量和箱壁的弹簧阻尼器参数。
基于Housner模型可以得出:液体高阶对流压力远小于一阶对流压力。因此,为了简化计算,本文模型中只考虑液体的一阶晃动,即将PCS水箱中液体的总质量分为脉冲质量和一阶对流质量。设PCS水箱液体体积为V,液体总质量为m,液面设计高度为h,内半径为Ri,外半径为Ro,参考已有研究成果[7-8],将非规则环形水箱等效成圆柱形水箱,等效半径R、一阶对流质量m1、一阶对流质量高度h1计算公式为
(1)
(2)
(3)
针对环形圆柱水箱,Meserole等给出了晃动力学模型的参数表达式,考虑到PCS水箱为底部锥形的非规则环形结构,本文首先将其等效为平底环形结构。如图3所示,基本思路是保证V,Ri和Ro不变,将PCS水箱等效成环形圆柱水箱,计算等效液面高度ha,求解晃动频率,计算公式为
(4)
λ=Ri/Ro
(5)
ki=(ha/Ro)ξi
(6)


(a)PCS水箱

(b)环形圆柱水箱图3 等效模型示意图Fig.3 Diagram of equivalent model
在PCS水箱简化模型中,将脉冲质量m0离散成质量点附加于水箱底部和水箱壁,参考ASCE4-98规范[9],认为液体竖向振动近似于刚性,将一阶对流质量m1分成水平分量mh和垂直分量mv,将mv离散成质量点附加于水箱底部。为了避免对流质量在动力计算过程中引起水箱壁局部应力集中,对mh进行分层离散处理,通过弹簧阻尼器连接于水箱壁,如图4所示。基于结构动力学基本公式,弹簧阻尼器的刚度和阻尼系数计算公式为
(7)

图4 液体晃动效应水箱简化模型Fig.4 Simplified sloshing model of water tank
式中:k和c为单个弹簧阻尼器的刚度和阻尼;K和C为弹簧阻尼体系的整体刚度和阻尼;n为弹簧阻尼器数目;ω1为一阶晃动频率;γ为晃动阻尼比。
2 结构反应数值分析
2.1 计算模型
采用ADINA软件建立核岛结构有限元模型,如图5(a)所示,X轴正方向为北,Y轴正方向为西,采用3D-Solid单元模拟核岛结构混凝土底板,3D-Shell单元模拟核岛结构墙体和楼板,3D-Beam单元模拟空间钢桁架。在流固耦合效应模拟方面,如图5(b)和图5(c)所示,模型1中采用流体单元模拟PCS水箱中的液体,模型2中采用简化模型模拟PCS水箱的FSI效应,模型材料参数见表1。

表1 数值模型材料参数Tab.1 Material parameters of numerical models

图5 核岛结构计算模型Fig.5 Numerical models of nuclear island building
2.2 结构模态分析
振动模态和频率是结构的固有特性,采用Lanczos法提取结构的振动模态和频率,结构前两阶自振频率及液体一阶晃动频率见表2。前两阶振动模态为核岛结构整体沿两个水平方向振动,两个模型前两阶频率相对误差均小于2%,液体一阶晃动频率相对误差小于1%。可以看出,本文PCS水箱简化模型可以较好地反映结构的动力特性。

表2 结构前两阶自振频率及液体一阶晃动频率Tab.2 The first two natural frequencies and 1st sloshing frequency
2.3 结构反应时程分析
选用典型的强震动记录El Centro地震动时程和基于核电厂标准设计反应谱拟合的人工地震动时程分别进行结构反应的时程分析,研究核岛结构地震反应。地震动采用三向输入,按照SSE(Safe Shutdown Earthquake)要求,峰值加速度均取0.3g[10-12],El Centro地震动和人工地震动三向加速度时程曲线和反应谱,如图6和图7所示。

图6 El-Centro地震动加速度时程和反应谱Fig.6 Acceleration time histories and response spectra of El Centro ground motion

图7 人工地震动加速度时程和反应谱Fig.7 Acceleration time histories and response spectra of artificial ground motion
考虑篇幅所限,本文选取屏蔽厂房西侧水箱顶部、水箱根部、支撑斜坡与筒体交界处3个观测点和辅助厂房顶部西南角1个观测点进行反应的具体分析,分别验证两个模型的地震反应在时域、频域以及液压效应方面的吻合情况。时域方面主要以观测点的峰值加速度作为对比参数,频域方面主要采用观测点的楼层反应谱进行对比分析,液压效应方面主要通过对比观测点处的有效应力时程曲线体现。4个观测点的具体位置见图5(a)。
2.3.1 结构反应的峰值加速度
计算结构反应并提取两个模型4个观测点在两组地震动下的峰值加速度。分析两个模型计算结果的相对误差,见表3,相对误差的计算公式为

(8)
表3中数据表明,两个模型各观测点反应的峰值加速度相对误差基本控制在5%以内,少数超过5%。该误差是由于简化模型本身采用了一些假定和简化处理,不能完全如实反应真实液体晃动情况造成的,但误差在可接受的范围内,可以认为计算结果吻合良好。

表3 结构反应的峰值加速度相对误差Tab.3 Relative errors of peak accelerations of structural responses
2.3.2 结构反应的楼层反应谱
根据加速度反应时程曲线计算得到楼层反应谱,图8列出了两个模型在El Centro地震动下4个观测点的楼层反应谱对比情况。在水平方向(X向、Y向),模型2的楼层反应谱曲线与模型1基本重合,在各个频段差异很小。在垂直方向(Z向),P1和P2两个观测点在结构基频对应的周期附近(0.10~0.30 s),两条曲线有一定的差异,在其他频段差异很小。两个模型的计算结果总体吻合良好。
图9列出了两个模型4个观测点在人工地震动下的楼层反应谱对比情况。与El Centro地震动计算结果相似,P1和P2两个观测点的垂直方向楼层反应谱在某些频段存在一定差异,两个模型计算结果总体吻合良好。
通过两个模型计算结果的对比分析可以进一步看出,对于两组特性(频谱和持时)差异很大的地震动,观测点楼层反应谱曲线的分析结果是一致的,说明提出的水箱简化模型在模拟FSI效应方面具有较好的适用性。针对某些频段(0.10~0.30 s)计算结果,为了更清楚地反映其差异大小,定量地分析两者的误差,提取加速度反应谱曲线在0.10 s,0.20 s,0.30 s时刻的数值和反应谱最大值,计算其相对误差,统计结果见表4和表5。相对误差采用式(8)计算。

表4 El Centro地震动下加速度反应谱值相对误差Tab.4 Relative errors of spectral accelerations under El Centro ground motion
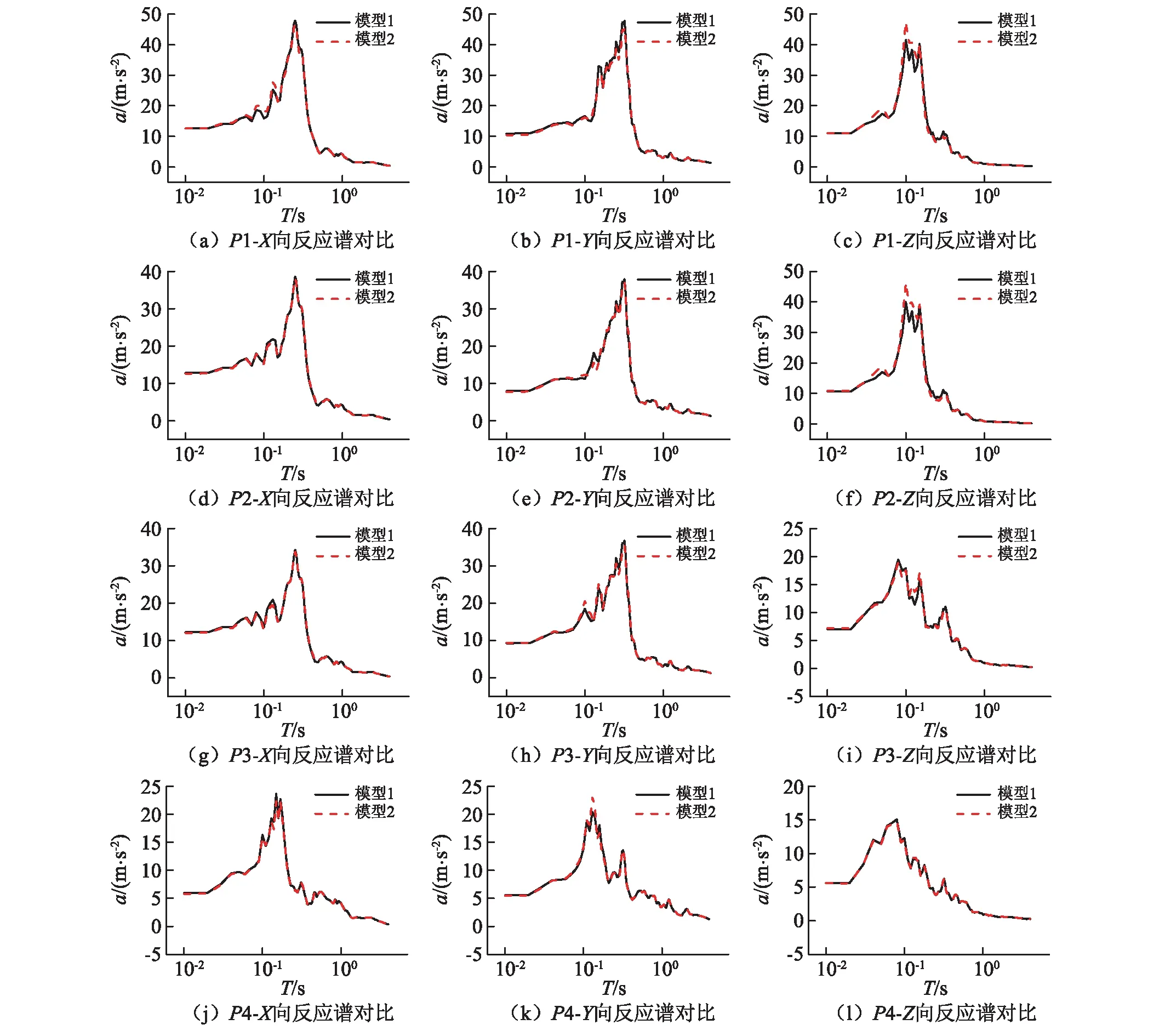
图8 El Centro地震动下观测点反应谱对比Fig.8 Comparison of response spectra under El Centro ground motion
图9 人工地震动下观测点反应谱对比Fig.9 Comparison of response spectra under artificial ground motion

表5 人工地震动下加速度反应谱值相对误差Tab.5 Relative errors of spectral accelerations under artificial ground motion
从表4和表5中可以看出,两个模型的楼层反应谱相对误差基本控制在10%以内,少数达到了12%左右。相对误差较大位置出现在水箱结构上的观测点(P1和P2),特别是在垂直方向,屏蔽厂房和辅助厂房上的观测点(P3和P4)相对误差较小。
PCS水箱简化模型中,在考虑水平地震作用时,基于Housner模型,将一阶对流质量m1的水平分量mh通过弹簧阻尼器连接于水箱壁来模拟水平晃动;同时在考虑竖向地震作用时,参考相关规范采用了液体竖向振动近似于刚性假定,将一阶对流质量m1的垂直分量mv附加在水箱底部。这些假定与真实竖向振动并不完全相符,加上PCS水箱底部倾斜,水箱外壁特别是根部(P2)受力情况复杂,简化模型并不能完全模拟真实情况。因此简化模型的计算结果在水平方向上更接近于流固耦合模型,垂直方向的误差相对较大。
通过图8、图9、表4和表5中的数据可以看出,水箱简化模型可以用于模拟考虑FSI效应的核岛结构动力分析,特别是水箱以下的主体结构,误差很小;对于水箱结构本身,采用简化模型存在一些差异。针对结构在三向地震动作用下的动力反应,水箱简化模型可以在保持计算结果合理的前提下,节省计算时间,提高计算效率。
2.3.3 结构反应的有效应力
由于简化模型无法输出液体动水压力,液体晃动效应作用在结构上主要体现在结构应力、应变的变化,因此,为了验证简化模型在模拟液体晃动和液压效应方面的合理性,提取4个观测点处的有效应力时程进行对比,如图10、图11所示。可以看出,在两组地震动作用下,P1观测点处两个模型的有效应力时程曲线形状基本相同,具体数值上有一定的差异,P2,P3,P4观测点处时程曲线基本重合。为了更清楚地反映差异大小,提取有效应力最大值进行比较,采用式(8)计算相对误差,如表6所示。P1观测点处有效应力最大值相对误差分别为8.30%和5.71%,P2,P3,P4观测点处相对误差均小于5.00%,4个观测点处相对误差控制在10%以内,认为两个模型计算结果总体吻合良好。

图10 El Centro地震动下观测点有效应力对比Fig.10 Comparison of effective stress under El Centro ground motion

图11 人工地震动下观测点有效应力对比Fig.11 Comparison of effective stress under artificial ground motion

表6 观测点有效应力最大值相对误差Tab.6 Relative errors of maximum effective stress
由于P1观测点位于水箱顶部,采用流固耦合模型计算时,能考虑到水箱顶部受液体晃动冲击的影响,而采用简化模型计算时,液体晃动效应通过“质量-弹簧-阻尼”系统模拟,由于对流质量高度有限,不能很好地考虑液体对水箱顶部的晃动冲击,存在一定的差异,造成有效应力的计算结果小于流固耦合模型。对于水箱下部和结构主体(P2,P3,P4观测点),简化模型能够很好地模拟结构反应的有效应力。
3 结 论
本文考虑核岛结构PCS水箱FSI效应,基于Housner模型提出一种适用于核岛结构三向地震反应分析的PCS水箱简化模型。在简化模型中,将液体分为脉冲质量和一阶对流质量,一阶对流质量的水平分量通过弹簧阻尼器连接于水箱壁,脉冲质量和一阶对流质量的垂直分量附加于水箱壁和底部。在此基础上,采用ADINA软件进行了高置冷却水箱核岛结构三向地震反应分析,对比了FSI模型和简化模型的计算结果,提取观测点结构反应的峰值加速度、楼层反应谱和有效应力,分析其相对误差。计算结果对比显示,PCS水箱简化模型可用于高置冷却水箱核岛结构的三向地震反应分析,能够很好地模拟FSI效应,在保证计算精度的情况下提高计算效率。

