常开洞工业厂房风致内压试验研究

樊友川，顾 明，全 涌

(同济大学土木工程防灾国家重点实验室，上海 200092)

0 引言

多次风灾调查表明［1－3］，由于建筑物门窗破坏等原因导致开洞，外部气流沿开洞传播，风致内压急剧增大，使得内外风压共同作用成为导致建筑结构破坏甚至倒塌的重要原因。文献［1］指出，在佛罗里达州风灾调查中，64%的民用建筑均因开窗，风压激增而导致破坏。因此，国内外许多学者运用现场实测［4－8］、风洞试验［9－13］与 CFD 数值风洞［14－15］等手段对建筑内压进行了大量的研究。大多数学者［6，10－12］重点研究了建筑结构迎风面瞬间开洞的内压脉动时程，并运用空气动力学理论推导了内压的响应方程。

工业厂房是一类开洞较多，开洞面积较大，且大多保持常开洞状态的建筑结构。Vickery［12］在湍流试验中发现结构瞬间开洞时内压脉动峰值较常开洞状态下的内压峰值小;Stathopoulos等［16］也通过风洞试验发现开洞建筑内压平稳值比开洞瞬间时的内压脉动大。本文通过风洞试验研究不同单个常开洞状态厂房结构内部压力系数的分布规律与形成机理，并根据理论公式对内压系数进行预测，为结构设计时内压的合理取值提供参考依据。

1 刚性模型风洞测压试验

风洞测压试验是在同济大学土木工程防灾国家重点实验室风洞试验室的TJ-2大气边界层风洞中进行的。该风洞是一座闭口回流式矩形截面风洞，试验段尺寸为宽 3m、高 2.5m、长 15m，试验风速范围从 0.5～68.0m/s连续可调。

风洞试验原型为单跨双坡工业厂房，纵向长度为90m，跨度为45m，高跨比为0.8，屋面坡角均为 3°。模型几何缩尺比为1∶100。模型为刚性模型，用3mm厚的有机玻璃板制成，如图1所示。模型均在一侧纵墙开洞。模型开洞形状、位置及其开洞率(开洞面积与纵墙面积的比值)如表1所示，模型示意图见图2。模型内外表面各布置测点221个，共442个测压点，图3为模型内表面测点布置图，外表面测点布置与之完全相同。测压管通过模型底部开孔与测压扫描阀连接以取得压力信号，同时将模型底部开孔用聚氯乙烯保温板封闭防止内部压力受底部开孔影响。以试验风垂直吹向纵墙平行于山墙方向为0°风向角，逆时针转动控制转盘增加风向角，取风向角间隔为22.5°，并加吹风向角15°、30°、60°以及 75°。

本次风洞试验的大气边界层流场为我国建筑结构荷载规范［17］中定义的A、B等两类风场，按照文献［18］的方法进行模拟。在风洞中选一个不受建筑模型影响，且离风洞洞壁边界层足够远的位置作为风场参考点，在该处60cm高度设置皮托管测量参考点静压总压。两类平均风速剖面的地貌地面粗糙指数 a分别为0.12、0.16。由于各类地貌的湍流度剖面我国规范尚未给出，且运用脉动系数计算得到的湍流度较其它国家的规范偏小许多。日本建筑物荷重指针(AIJ2004)［19］通过实测得到湍流度剖面并拟合出公式，本次风洞试验采用该湍流度公式。图4给出了A类风场的模拟结果以及模型屋盖平均高度处纵向风速谱。

文献［7］指出，为了正确模拟内压脉动特性，结构长度缩尺比［L］r、体积缩尺比［V0］r与风速缩尺比［U］r必须满足，所以选取试验风速比为1∶1以保证正确模拟内压。试验风速为15m/s(模型屋盖平均高度处)，采样频率为312.5Hz，每个测点采样样本长度为9000个数据。试验模型几何缩尺比为1∶100，风速比为1/1，则频率比为100，实际采样频率为3.12 Hz。采用文献［20］的方法修正了测压管道对测量信号的影响。风洞试验测量的压力数据通常用无量纲化的风压系数表示为:

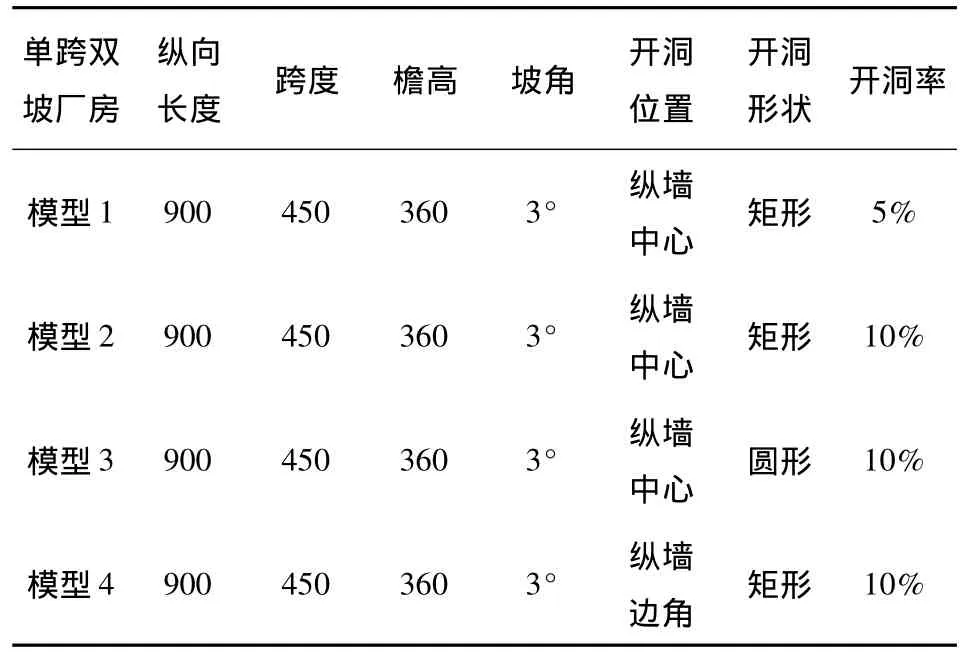
表1 刚性模型详细参数(mm)Table 1 Wind tunnel model parameters

式中，Cp为测点的风压系数，P为作用在测点上的风压，ρ为空气密度，Vh是参考高度处风速，这里取屋盖平均高度作为参考高度。风压系数的符号约定指向受压面为正，反之为负。

2 内压分布规律及其脉动机理

图5给出了在0°风向角下模型2内部三个测点1-1、1-28和3-19(图2)上的风压系数时程曲线。由图5可知，结构内部测点时程曲线几乎完全相同。图6给出了模型1在0°风向角时内压系数平均值和均方根值的等值线图，内压均值及均方根值空间分布非常均匀，几乎处处相等，仅在开洞附近测点的风压值稍有差别。对于单开洞建筑，其内部空气对流微弱，在给定边界的空间中空气以声速传播压力，内部压力瞬间达到相等，内部测点压力空间完全相关。因此，可以用统一的时程曲线来代表单开洞结构内压的特性。

图7为0°风向角时模型3的脉动内压系数与开洞纵墙外表面脉动风压系数的相干函数。约5Hz以下的低频部分，开洞纵墙面测点的外压与内压相关性很强，由此可见内压与开洞纵墙面外压的低频段脉动均来源于来流风的湍流作用。图8给出了0°与45°风向角时内压系数与开洞墙面外压系数的自功率谱。0°与45°风向角时内压在频率约90Hz左右产生赫姆霍兹共振，根据文献［22］可计算出模型3赫姆霍兹频率理论值为95Hz，可见试验测得的赫姆霍兹频率与理论预测值吻合得较好。45°风向角时频率约20Hz处内压自功率谱能量值数倍于低频段能量值，这一现象是洞口附近的旋涡脱落导致的。文献［21］在风洞试验中改变试验风速导致旋涡脱落频率与赫姆霍兹频率接近时，激起了较大能量的赫姆霍兹共振。内压最大极值可能发生在斜风向工况，所以应尽量避免旋涡脱落频率靠近赫姆霍兹频率。综上所述，常开洞建筑内压脉动主要源于三个方面:来流湍流作用直接引起的风压脉动;旋涡脱落、尾流干扰等引起的内压脉动;赫姆霍兹共振导致的内压脉动。

3 内压随风向角变化规律

图9(a)为模型内压系数的均值随风向角变化曲线。模型纵墙中心开洞时，内压系数均值随风向角的变化规律一致。0°风向角的内压系数均值最大，模型1为0.54，模型2 为0.67，模型3 为 0.67。随着风向角的增大，内压系数均值不断减小，约75°风向角时内压系数均值减小至0;当风向角增大至135°，模型1～3内压系数均值取得最小，分别为 －0.50、－0.56 与 －0.54。当开洞墙面处于背风面时，三个模型内压系数均值很接近，约为－0.23。当模型纵墙面边角开洞时，内压系数随风向角的变化规律与中心开洞时不同。模型4为边角矩形开洞，30°风向角时内压系数均值为最大，为0.50;约65°时，内压系数均值减小至0;与中心开洞模型类似，其最小值也出现在135°，为 －0.64;180°风向角时内压系数均值为－0.30。

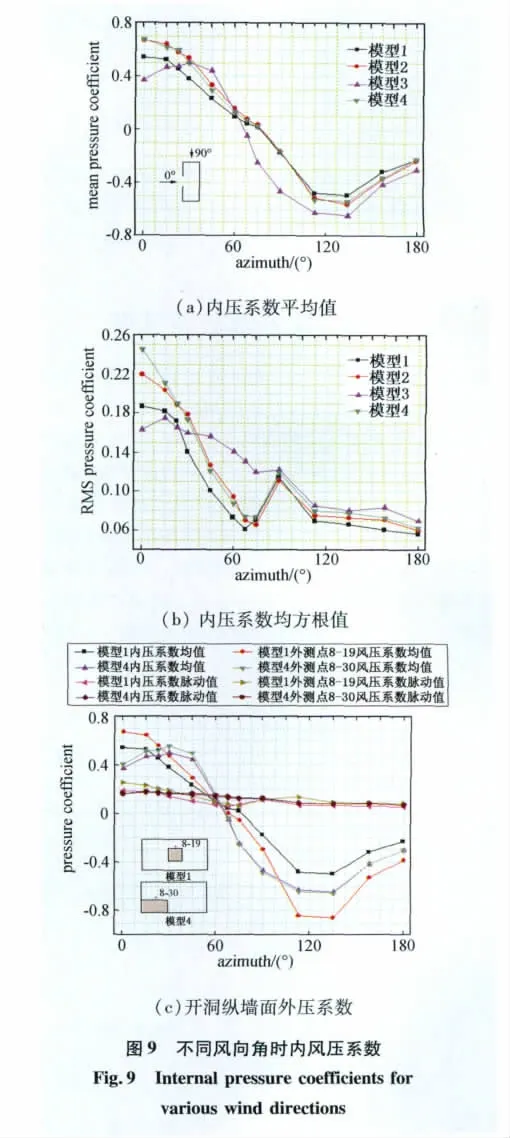
如图9(b)所示，内压系数的均方根值变化规律与其均值类似，模型纵墙中心开洞时，内压系数均方根值随风向角的变化规律一致。0°风向角时内压脉动最大，模型1 ～3 的均方根值分别为 0.19、0.22 与0.25。随着风向角的增大，脉动值总体趋势逐渐减小，180°风向角时，脉动最小，其值为0.06。当模型纵墙边角开洞时，内压脉动约15°时为最大，内压均方根值为0.18;内压脉动随风向角增大而减小，但其减小的幅度较中心开洞时为小。在风向角为90°时，内压脉动值突增，这是由于中心开洞模型90°风向角时，旋涡脱落引起的脉动能量较60°与75°风向角时为大，与45°风向角时能量接近;而边角开洞模型90°风向角时脉动能量与75°风向角时接近。

文献［21］指出，内压脉动值受开洞赫姆霍兹频率无量纲化的斯托罗哈数影响，而不同斯托罗哈数的内压脉动值随风向角的变化趋势具有一致性。由于试验条件的限制，本文试验没有特别考查斯托罗哈数对内压的影响。根据文献［21］计算，本文试验模型洞口的斯托罗哈数在0.5左右，故本文所讨论的内压系数均方根值为斯托罗哈数在0.5左右的情况。

图9(c)为不同风向角时模型1与模型4开洞附近外测点8-19与8-30的风压系数。由图可知，内压系数与开洞附近外测点风压系数随风向角变化趋势基本一致，这就进一步说明了内压与开洞纵墙面外压具有较强的相关性。

4 不同开洞情况内压

图10给出了不同风向角时各种开洞情况的内压系数均值及其均方根值。模型2较模型1中心开洞面积增大，其内压系数均值与脉动值均不同程度的增大。在最不利正内压即0°风向角时，模型2较模型1的内压系数均值提高0.13;在30°风向角时，两者相差最大，为0.16;随着风向角的增大，两者的差别减小，特别是在180°风向角时，两者的内压系数均值与均方根值几乎相等。如图所示，模型2矩形开洞与模型3圆形开洞时，两者的内压系数均值几乎相等。开洞形状对于内压系数均值几乎没有影响;而内压系数均方根值受开洞形状有所影响，0°风向角时圆形开洞的内压均方根值较矩形开洞为大，随着风向角的增大，两者的均方根值几乎相等。与中心矩形开洞相比，边角开洞可以较大程度的减小最不利正内压。模型4的最不利正内压出现在30°风向角工况，内压系数均值较模型2减小约0.17，均方根值减小约0.02。但在最不利负内压即135°风向角时，模型4较模型2的内压系数均值绝对值略大，约0.08;而内压均方根值几乎相等。

5 风场类型对于内压的影响

图11为模型2在A、B两类风场时的内压系数。A类风场时内压系数均值较B类风场稍大，而由于湍流度的提高，B类风场的内压系数的均方根值较A类风场稍大。来流风场对内压影响较小。

6 单开洞结构内压的理论分析和试验结果的比较

6.1 稳态理论［22］

根据稳态理论［22］，假设理想不可压缩流体作定常运动，由伯努利方程可得多开洞洞口内压计算公式为

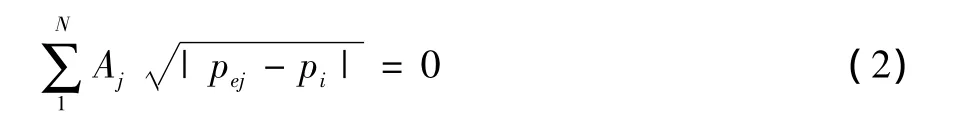
式中，pej为 j洞口处外压，pi为内压。

当建筑只有单一开洞时，有

式中，Cpw和Cpi分别为开洞洞口处外压系数和结构内压系数。

因此，单开洞建筑的内压系数可以用开洞附近外表面各测点风压系数的平均值估算。

图12为四个模型内压系数计算值与内压系数试验值。由图可知，稳态理论运用于平均内压的估计可以得到较为精确的结果，特别是在最不利工况即0°风向角时，最大相对误差仅为5%;在最大负内压工况即135°时，最大相对误差仅为7%。但是模型的内压脉动估计值普遍偏大，最大误差为模型1在0°风向角工况，为32%。边角开洞模型即模型4的脉动估计值相对准确，这是由于模型4纵墙边缘即为洞口边缘，内压与洞口附近外压均受纵墙边缘旋涡脱落影响，具有相同的脉动能量来源。而中心开洞模型鉴于洞口附近外压与内压脉动机理不同，所以采用稳态理论计算内压脉动值通常不准确，实际设计中采用稳态理论计算内压峰值会取得偏安全的结果。

6.2 非定常方法

各国学者对于内压值的非定常响应方程的形式已经达成共识［10－11］，即用二阶非线性常微分方程来描述内压与外压的关系。Vickery［23］认为外压与内压的差值主要来自于流体经过洞口的压力损失以及入流气团运动的惯性，并推导出了考虑洞口损失的内压响应方程:

式中，Cpi为结构内压系数为结构开洞洞口处外压系数脉动值A为开洞面积，CI为惯性系数，V0为结构内部体积，Ka为空气的体积弹性模量，ρ为空气密度，CL为气体经过开洞洞口摩擦损失系数，VR为参考风速，fHH为赫姆霍兹频率。

由前文内压脉动机理可知，在0°风向角时，内压脉动主要来源于来流风湍流和赫姆霍兹共振，故而将外压时程作为荷载项代入公式(4)求解内压时程是合适的。运用四阶龙格库塔方法求解内压响应方程，图13为模型2在0°风向角时内压脉动时程的试验值与模拟值。由图可以看出，非定常方法预测的内压时程与试验内压时程非常相似，当洞口摩擦损失系数CL取为45时，模拟效果较好。图14给出了0°风向角时四个模型内压均方根的试验值与计算值。由图可知，非定常方法计算所得的内压均方根值与试验非常接近，其最大相对误差为8%。在斜风向条件下，内压脉动的一部分能量由旋涡脱落、尾流干扰等提供，所以必须在内压响应方程的右端添加修正项Ceddy，即

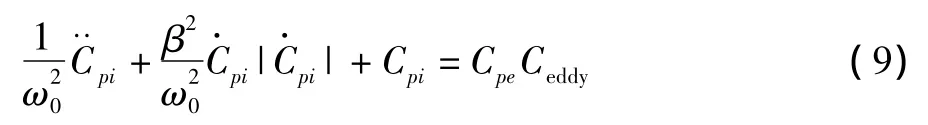
但是目前为止修正项Ceddy的机理和理论公式尚不完善［20］，所以非定常内压响应方程(4)对斜风向条件下的单个常开洞建筑的内压预测是不适用的。

7 结论

本文通过一系列不同单个常开洞条件的刚性工业厂房模型风洞测压试验，深入研究了建筑内压的分布规律以及脉动机理，分析了不同开洞条件对内压的影响，同时，运用稳态理论与非定常内压响应方程对试验内压进行了预测，得到如下结论:

(1)单个常开洞厂房的内压空间分布均匀，几乎处处相等，仅在开洞附近测点的风压值稍有差别;内压的脉动特性主要来源于来流湍流作用、旋涡脱落、尾流干扰以及赫姆霍兹共振等三个方面的影响。

(2)风向角对建筑内压影响较大。对于纵墙面中心开洞建筑，0°风向角时内压系数均值与均方根值最大;对于纵墙面边角开洞建筑，30°风向角时内压系数均值最大，15°风向角时内压系数均方根值最大。两种模型均在135°风向角时内压系数均值最小(最大负值)，180°风向角时内压系数均方根值最小。

(3)随着中心开洞面积增大，建筑内压系数均值与均方根值均不同程度增大。开洞形状对于内压系数均值几乎没有影响;而内压系数均方根值受开洞形状有所影响。与中心开洞相比，边角开洞可以较大程度地减小最不利正内压。

(4)风场类别对内压影响较小。随着湍流度的提高，B类风场内压系数的均方根值较A类风场大，内压系数均值略有降低。

(5)稳态理论能够较好地预测内压系数均值，但是预测均方根值偏保守。非定常理论推导得到的内压响应方程对0°风向角工况内压时程可以得到良好的预测，但由于受旋涡脱落、尾流干扰等影响，斜风向时运用内压响应方程预测内压是不合适的。

［1］Assessment of damage to single-family homes caused by hurricanes Andrew and Iniki［R］.Washington D.C:U.S.Department of Housing and Urban Development，1993.

［2］Hurricane Katrina in the Gulf Coast［R］.U.S.Department of Homeland Security，2006.

［3］SHANMUGASUNDARAM J，ARUNACHALAM S，GOMATHINAYAGAM S，et al.Cyclone damage to buildings and structures — a case study［J］.J.Wind.Eng.Ind.Aerodyn，2000，84∶369-380.

［4］LEVITAN M L，MEHTA K C.Texas Tech field experiments for wind loads part 1.Building and pressure measuring system［J］.J.Wind.Eng.Ind.Aerodyn.，1992，43 ∶1565-1576.

［5］LEVITAN M L，MEHTA K C.Texas Tech field experiment for wind loads part II:meteorological instrumentation and terrain parameters［J］.J.Wind.Eng.Ind.Aerodyn.，1992，43(1-3)∶1577-1588.

［6］GINGER J D，MEHTA K C，YEATTS B B.Internal pressures in a low-rise full-scale building［J］.J.Wind.Eng.Ind.Aerodyn.，1997，72(1-3)∶163-174.

［7］GINGER J D，LETCHFORD C W.Net pressures on a low-rise full-scale building［J］.J.Wind.Eng.Ind.Aerodyn.，1999，83∶239-250.

［8］SHARMA R N，RICHARDS P J.Net pressures on the roof of a low-rise building with wall openings［J］.J.Wind.Eng.Ind.Aerodyn.，2005，93(4)∶267-291.

［9］余世策，楼文娟，孙炳楠，等.开孔结构内部风效应的风洞试验研究［J］.建筑结构学报，2007，28(4)∶76-82.

［10］HOLMES J D.Mean and fluctuating internal pressures induced by wind［P］.IN∶Proc.Fifth Int.Conf.On Wind Engineering，(FORT Collins，U.S.A.:Jul.8-14，1979).CERMAK J E(ED)，1979，1 ，New York，U.S.A.，Pergamon Press，1979，Session IV，Paper 8.

［11］LIU H，SAATHOFF P J.Building internal pressure:sudden change［J］.ASCE J.Eng.Mech.Div.，1981，107(2)∶309-321.

［12］VICKERY B J.Gust-factors for internal-pressures in low rise buil dings［J］.J.Wind.Eng.Ind.Aerodyn.，1985，23(1-3)∶259-271.

［13］WOODS A R，BLACKMORE P A.Effect of dominant openings and porosity on internal pressures［J］.J.Wind.Eng.Ind.Aerodyn.，1995，57(2-3)∶167-177.

［14］SHARMA R N，RICHARDS P J.Computational modelling of the transient response of building internal pressure to a sudden opening［J］.J.Wind.Eng.Ind.Aerodyn.，1997，72(1-3)∶149-161.

［15］SHARMA R N，RICHARDS P J.Computational modelling in the prediction of building internal pressure gain functions［J］.J.Wind.Eng.Ind.Aerodyn.，1997，(67-68)∶815-825.

［16］STATHOPOULOS T，LUCHIAN H D.Transient wind-induced internal pressures［J］.Journal of Engineering Mechanics，1989，115(7)∶1501-1514.

［17］GB50009-2001［S］.建筑结构荷载规范.

［18］黄鹏，顾明.风洞中模拟大气边界层流场的方法研究［J］.同济大学学报，1999，27(2)∶136.

［19］Architectural institute of Japan［S］.AIJ Recommendations for Loads on Buildings(English version)，2004.

［20］周晅毅.大跨度屋盖结构风荷载及风致响应研究［D］.［博士学位论文］.同济大学，2004.

［21］SHARMA R N，RICHARDS P J.The influence of Helmholtz resonance on internal pressures in a low-rise building［J］.J.Wind.Eng.Ind.Aerodyn.，2003.91(6)∶807-828.

［22］HOLMES J D.Wind loading of structure［M］.UK:Taylor＆Francis，2007.

［23］VICKERY B J，BLOXHAM C.Internal pressure dynamics with a dominant opening［J］.J.Wind.Eng.Ind.Aerodyn.，1992，41(1-3)∶193-204.