运输机短舱挂架纵向位置优选数值研究

雷熙薇，桑为民，段卓毅，冯海勇，张彦军

(1西北工业大学翼型、叶栅空气动力学国防科技重点实验室，陕西西安 710072)(2中航工业第一飞机设计研究院，陕西西安 710089)

0 引言

现代运输机多采用翼吊涡扇发动机布局，发动机及其进排气系统对飞机气动性能有明显影响。

实践表明，短舱、挂架对机翼绕流的影响区域并不仅局限于其附近翼面，几乎整个机翼绕流均受其影响。超临界机翼上的压力分布对挂架外形以及短舱相对于机翼的空间位置相当敏感［1－2］，发动机的安装改变了通过机翼的绕流，在翼/身/架/舱(WBPN)之间形成的“通道”中存在强烈的干扰流场:比如激波提前产生和增强而形成分离;挂架前缘与机翼前缘绕流的干扰;翼下短舱和挂架对机翼整个绕流流场的干扰影响等。

这些干扰的影响很大，特别是对于大旁通比的发动机，干扰阻力可达全机阻力的3%左右，而巡航阻力每降低1%，可减少飞机直接使用成本1.2%［3］。因此，找出短舱挂架的最优配合位置，精确预测翼/身/架/舱干扰影响，对于评估飞机气动性能和操稳特性是十分必要的。

通过试验及理论计算两个途径可以分析并解决上述干扰问题。以前，由于机翼与短舱、挂架的干扰机理十分复杂，该类干扰影响的研究工作主要由风洞试验完成。现在，由于计算机技术的高速发展及计算流体力学(CFD)方法的日益完善，对复杂流场进行数值分析已成为可能，并有快速、灵活和成本低等优点。

本文使用CFD方法对短舱挂架的纵向位置进行优选分析，得出优选配合位置，减小翼/身/架/舱之间的干扰影响，具有工程应用价值。

1 数值方法

1.1 计算方法及控制方程

面元法虽然计算速度快，但对于解决激波及大分离问题较弱;N-S方程虽然计算结果准确，但它的计算速度较慢，计算代价大;Euler方程不仅计算速度较快，而且计算结果趋势准确，适于初始方案阶段的快速选型。所以最终选用Euler方程(MGAERO软件)进行本文优选数值研究。

MGAERO软件采用笛卡尔网格，应用有限体积法求解三维Euler方程，计算绕任意几何外形的三维可压流动，应用了当地时间步长、隐式残值光顺以及焓阻尼和多重网格技术等多种加速收敛措施。由于采用了均匀网格，Euler方程的离散在空间能达到二阶精度;在时间上采用多步显式 Runge-Kutta方法推进求解［4－5］。MGAERO软件可以准确地捕捉不同构型之间的气动力差量，计算结果趋势与试验符合较好，尤其是在跨声速、超声速及在马赫数不小于0.3的亚音速，但它不适于计算大迎角复杂高速构型及马赫数小于0.2的低速构型［5］。

可压缩流体运动的Euler方程:

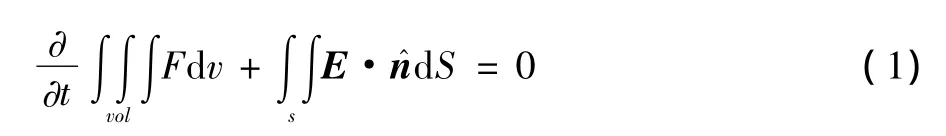
通量矢量E表示为

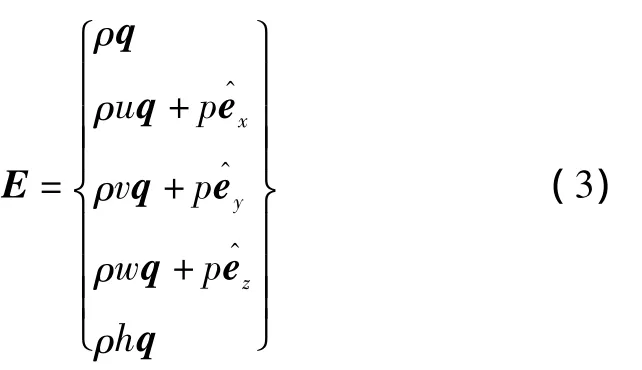
1.2 计算网格

本文采用笛卡尔网格对WBPN简化构型进行纵向气动特性Euler方程计算(由于本文目的是快速方案选型优化，较注重差量对比)，共7层网格，网格数为2，607，475，对外形曲率变化较大处进行了局部网格加密，获得的空间网格如下图1所示。

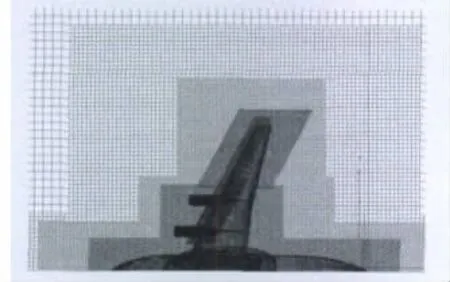
图1 空间网格Fig.1 Space grids

1.3 计算方法验证

为了验证计算方法的可靠性和准确性，我们选取了某飞机标模的纵向半模构型进行计算验证。计算状态为 M=0.85，Re=4.9830 ×106(基于平均气动弦长)。计算极曲线与试验数据对比如图2所示。可以看出计算结果与试验结果吻合较好，精度满足工程分析需要。其他大量算例也验证了本文计算方法的可靠性与准确性［4，8 －10］。

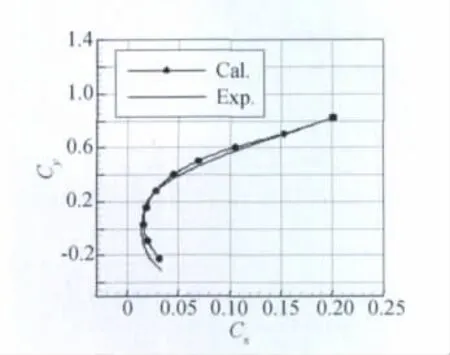
图2 极曲线(M=0.85)Fig.2 Drag coefficient curve(M=0.85)

2 前伸量、下沉量定义与选取

如图3所示，前伸量定义为X/C，X为该处外涵喷口到机翼前缘的纵向距离，C为该处翼弦弦长，下沉量定义为h/D，h为该处机翼下翼面切线与短舱上表面切线的距离，D为外涵喷口直径。本文短舱挂架前伸量、下沉量的初始位置为:

内侧短舱:X/C=0.2332、h/D=0.3787、展向位置27%

外侧短舱:X/C=0.2756、h/D=0.3502、展向位置48%

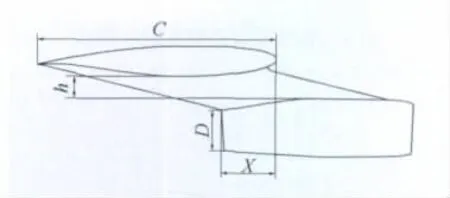
图3 短舱挂架前伸量和下沉量定义图Fig.3 Definition of the protrusion and subsidence

前伸量是翼/身/架/舱干扰影响的关键因素，是短舱沿纵向距干扰速度场远近的标志，下沉量不仅是影响短舱/机翼干扰的重要因素，也是衡量发动机吸进地面杂物可能性的重要因素之一［11］。

根据俄罗斯中央空气流体动力研究院对运输机的研究经验［12］，前伸量最佳范围为 0.143 ～0.161，最佳值在0.152 左右;下沉量最佳范围为 0.187 ～0.342，最佳值在0.264左右。本文参考给定运输机的初始几何外形，先固定初始下沉量，选取 －0.1、0.0、0.1、0.2 和 0.3五个前伸量位置进行计算，选取阻力最小的为优选前伸量;再固定初始前伸量，选取 0.2、0.4、0.6、0.8 和 1.0五个下沉量位置进行计算，选取阻力最小的为优选下沉量;最后把优选前伸量与下沉量配合在一起，得出纵向优选位置。

图4、图5 分别给出了 M=0.74、0.78 时前伸量和下沉量对升阻特性的影响，其中纵坐标为WBPN与WB(翼/身)构型的阻力差量(WB的计算值也是由本文计算方法获得)。当 M=0.74、Cl=0.51 时，前伸量为 0.1的WBPN 构型，阻力差量减小12.5%;当M=0.78、Cl=0.51时，下沉量为0.2的 WBPN构型，阻力差量减小4.92%。所以选取优选前伸量为0.1，优选下沉量为0.2。可见，前伸量比下沉量的减阻贡献大，小升力系数时更为明显。所以，短舱挂架的纵向优选配合位置为:前伸量0.1+下沉量0.2，如图6所示。

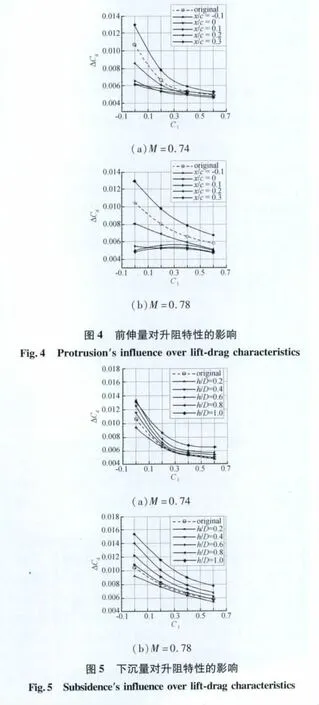
图6 优选配合位置与初始位置对比图Fig.6 Comparison between the optimized location and the original location

3 优选位置与初始位置气动特性对比

3.1 阻力特性

图7为M=0.74、0.78时短舱挂架的优选配合位置与初始位置的阻力比较，减阻量是可观的。图8为M=0.74时优选配合位置的减阻量与初始位置干扰阻力的比较，可见位置优选后，小升力系数下干扰阻力减少量很可观，但不能完全消除干扰阻力，因为干扰阻力的产生与下翼面的速度增量直接相关，小升力系数时，下翼面的速度高，易产生激波，随升力增加，下翼面速度降低，干扰减弱。

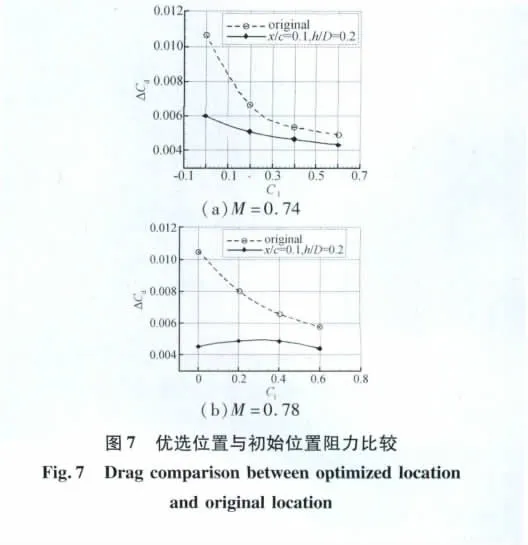
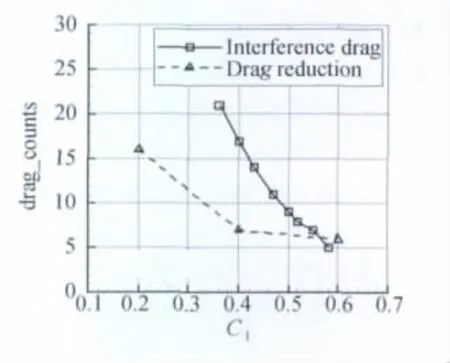
图8 优选位置减阻量与初始位置干扰阻力比较(M=0.74)Fig.8 Comparion between the drag reduction of optimized location and the interference drag of original location(M=0.74)

3.2 升力、俯仰力矩特性

从图9和表1可以看出，优选配合位置的升力及俯仰力矩特性均优于初始位置。

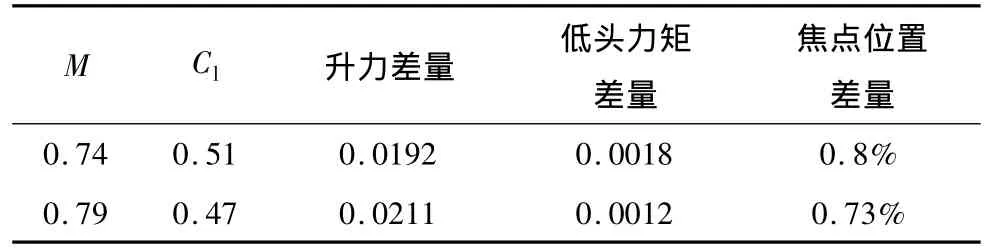
表1 优选配合位置相对于初始位置的气动力差量Table 1 Difference of the aerodynamic force between the optimized location and original location

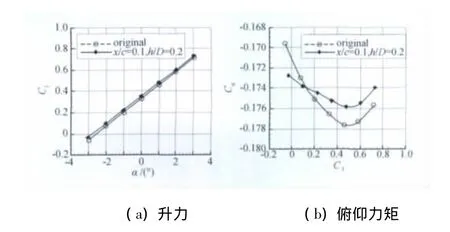
图9 优选配合位置与初始位置升力、俯仰力矩比较(M=0.74)Fig.9 Comparison of lift and pitching moment between the optimized location and original location(M=0.74)

3.3 压力分布特性

图10、图11 为 M=0.79，α =1°时短舱挂架优选配合位置与初始位置的压力分布及机翼下表面等压线云图对比。

从图11可以看出，翼根与内侧短舱间原有的较强激波在优选后明显减弱。优选后的位置对减小波阻是比较有利的，这主要得益于以下三方面:一是面积率有所改善，短舱挂架前移后与机翼的面积重叠有所错开;二是前移和上移后的挂架后掠角增加;三是优选后的位置短舱后缘处于机翼下翼面前缘附近，而短舱后缘的气流速度较低，这对减缓下翼面的压力变化是有利的。

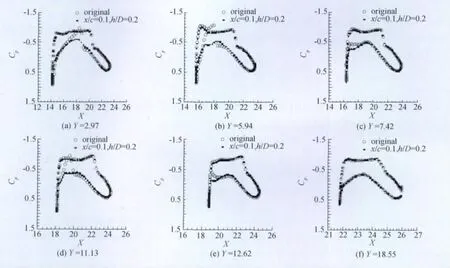
图10 优选配合位置与初始位置压力分布对比图(M=0.79，α=1°)Comparison of the pressure distribution between the optimized location and original location(M=0.79，α =1°)

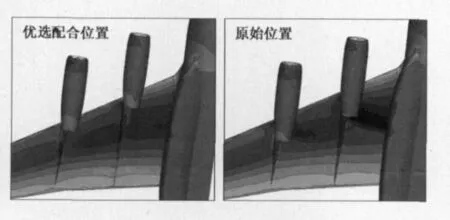
图11 优选配合位置与初始位置下翼面等压线云图对比Fig.11 Comparison of the Pressure Contour between the optimized location and original location

4 结论

1)经过计算分析，选出前伸量0.1+下沉量0.2为本文短舱挂架的纵向优选配合位置;

2)短舱挂架位置优选后，气动干扰明显减小，减阻贡献较大，升力及俯仰力矩特性也得到改善，从压力分布看，下翼面波阻明显减小;

3)在分析翼/身/架/舱干扰问题的同时，还要兼顾对低速特性的影响，如:短舱是否与前缘缝翼产生几何干涉;位置优选后的发动机喷流是否会打到后缘襟翼上;短舱上移是否会导致抖振边界及阻力发散问题等;

4)翼吊布局运输机的翼/身/架/舱干扰问题比较复杂，本文得出的只是一个初步的数值计算结论，其分析计算思路在初始选型设计中已得到应用，对后续的短舱挂架位置详细设计具有指导和参考价值，在此基础上还需进一步开展相关的风洞试验研究。

［1］王修方.翼下吊挂短舱的布局讨论［J］.民用飞机设计与研究，1997，16(3):12-16.

［2］LI J，LI F W，QIN E.Numerical simulation of transonic flow over wing-mounted twin-engine transport aircraft［J］.Journal of Aircraft，2000，37(3):469-478.

［3］方宝瑞.飞机气动布局设计［M］.北京:航空工业出版社，1997.

［4］左志成，陈迎春，段卓毅.前后缘机动襟翼数值计算研究［J］.飞行力学，2004，22(3):73～75.

［5］ESI公司.MGAERO 用户手册(3.1.4版本)［M］.北京:AMI公司，2000.

［6］ANDERSON D.计算流体力学入门［M］.北京:清华大学出版社，2002.

［7］张聘义，徐劲祥，王子梁，祁载康.欧拉方程计算气动力时的粘性修正研究［J］.弹箭与制导学报，2003，23(3):59-64.

［8］PETRUZZELLI N，KEANE A J.Wave drag estimation for use with panel codes［J］.Journal of Aircraft，1999，38(4):778-782.

［9］LIU H，WU Z.Automated scheme adjustment for conceptual aircraft design and optimization［J］.Journal of Aircraft，2006，43(3):825-831.

［10］GURSUL I.Proposed mechanism for time lag of vortex breakdown location in unsteady flows［J］.Journal of Aircraft，2000，37(4):733-736.

［11］《飞机设计手册》总编委会.《飞机设计手册》(6)［M］.北京:航空工业出版社，2002.

［12］凌茂芙.他山之石［M］.北京:航空工业出版社，1996.