弹性悬挂弯扭耦合颤振模型表面压力分布的时空特性及颤振机理分析

周志勇，杨立坤，葛耀君

(1.同济大学土木工程防灾国家重点实验室，上海 200092;2.天津市市政工程设计研究院，天津 300000)

0 引言

桥梁风致振动所有问题从本质上讲是流体和结构耦合振荡所致的动力相互作用问题，是能量传递的问题，对发散性的颤振表现地更加明显。桥梁颤振失稳可以分为单自由度(1DOF)扭转颤振和两自由度(2DOF)弯扭耦合颤振。Scanlan［1］提出可由8个气动导数表征主梁断面几何外形的气动力特性，从工程应用角度，Scanlan提出的气动导数可确定大跨桥梁颤振稳定性能。

值原Tacoma桥倒塌50周年之际，英国 WYATT［2］提出:平板古典耦合颤振和钝形断面的分离流扭转颤振是二种不同的机制，尽管通过风洞试验能保证安全的抗风设计，但流体和结构的相互作用机理是不清楚的。

目前，桥梁颤振机理的研究主要有三类方法，分别是基于气动导数的颤振驱动机理分析方法、基于计算流体动力学(CFD)的方法及基于粒子图像测速技术(PIV)的方法。

基于气动导数的颤振驱动机理分析方法首先通过节段模型风洞试验识别的断面气动导数，然后进行二维或三维颤振分析。基于分步分析的思路，杨咏欣［3］用二维三自由度分析方法研究了二维桥梁节段模型扭转、竖向和侧向振动参数(系统阻尼及系统刚度)同断面气动导数的定量关系及颤振发生点各个自由度运动的耦合效应。

丹麦的 Larsen［4］利用二维随机离散涡方法软件(DVMFLOW)，显示了原Tacoma桥断面绕流流动和结构相互作用的全过程。研究表明旋涡沿主梁的漂移会使升力的作用点同时漂移，造成升力矩从正向负转化，当涡的间距和桥面跨度达到一定的配合关系将激起发散的扭转振动。然而值得商榷的是，Larsen在数值计算中假定Tacoma桥的扭转颤振风速仅与旋涡的漂移速度相关且旋涡沿桥梁断面(原Tacoma桥断面)的漂移速度是恒定不变的，而以单个因素的线性化假设并不能描述流体的粘性与断面非定常运动的耦合的强非线性特征。

PIV技术是一种20世纪80年代发展起来的流场测试手段，能够捕捉到涡量沿断面及在尾流流动中的瞬时状态。张伟［5］应用PIV技术对H形桥梁断面运动及静止状态的旋涡运动进行了分析。分析认为H形桥梁断面的风振驱动是由于上下腹板交替移动的旋涡造成的，而旋涡是由于前缘竖板引起的流动分离形成的。在一个完整的周期内，结构表面的旋涡经历了从生成到脱落的过程。但限于较低的时间分辨率、较小的模型比例，试验还未能对颤振全过程进行系统地采样及分析。

POD(Proper Orthogonal Decomposition)技术提供了一种描述结构表面风压场的统计方法，它将风压场分解为仅依赖时间的主坐标和仅依赖空间的协方差模态的组合。POD可以找出一系列随机过程之间的隐藏在已知数据背后的特征，其最大的优点就是用很少的几个模态去表述一个过程，而通常主要模态和现象的机理是有很大关系的［6－9］。在钝体空气动力学中，POD技术常被用来针对风洞试验或实测所获得结构表面压力，来构建简化气动模态和分析结构上风荷载的主要机理。上述过程主要是通过把气动荷载或压力看做一个确定时间内的n维随机过程，把POD分析看做一个线性变换过程，把压力数据和力的分布展开成一系列用零延迟协方差矩阵特征向量表达的模态。Armitt［7］最早将POD技术用于风工程，1990年Holmes［8］分析了一个低矮建筑模型边跨的压力，讨论了POD模态与暗含的物理现象之间的联系。1995年Bienkiewicz等人［9］研究了边界层风洞中的一座低矮建筑，使用分布在建筑表面的494个测点同步测量，基于POD技术获得相关本征模态。

现有的测压技术的采样频率可设置的很高(大于300Hz)，在二元弹性悬挂刚体模型断面上布置测压点，以较长的采样时间测量断面颤振前及颤振过程中的表面压力的变化，既可避免仅基于气动导数进行颤振驱动机理分析的短处，又可避免PIV技术中较低的时间分辨率(15Hz)、不能对颤振全过程进行系统地采样及不能得到断面同步的表面压力的缺点。

目前对应于桥梁颤振时的断面压力空间分布特征是不清楚的。本文第2节简述了POD方法的基本数学格式。第3节介绍二元弹性悬挂刚体模型表面压力采样试验，试验风速逐级增加直至颤振发生，对模型颤振时及固定时(来流风速与颤振风速一致)的表面压力进行采样，分析了模型颤振时的表面压力分布特征。第4节运用POD方法分析模型表面压力分布与颤振分散性运动之间的关系。本文工作目前未见报道，为今后颤振机理分析提供了一个新的思路与方法。

1 POD方法的基本数学格式

假设p(x，y，t)为随机脉动风压力函数，那么p(x，y，t)的协方差函数 Cp(x，y，x'，y')可写成:

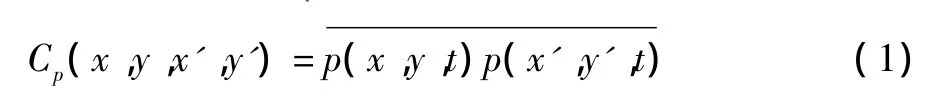
式(1)的特征值问题为:

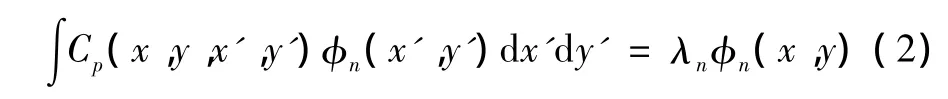
式中，φn(x，y)及λn是式(2)所示特征值问题求解所获得的本征模态及特征值，并且有

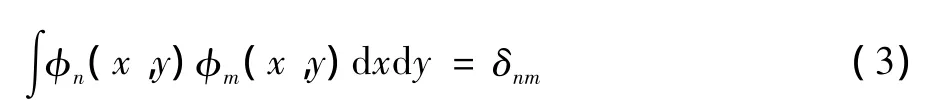
其中，δnm为 kronecker符号

当且仅当λn及φn(x，y)分别是协方差函数Cp(x，y，x'，y')的特征值及相应的标准正交的特征模态时，随机风压函数p(x，y，t)可以展开成下式:

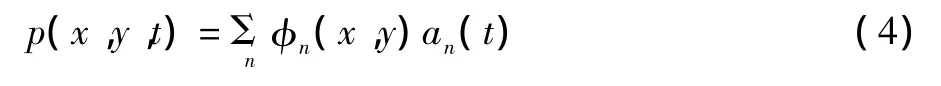
对第i个测压点的脉动风压力则有

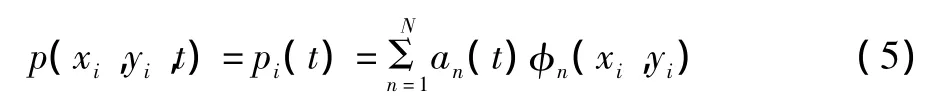
式中 φn(xi，yi)为本征模态 φn在测压孔(xi，yi)处的值。上述两式即脉动风压力向量及脉动风压力的本征正交分解，其意义是结构表面随时间和空间变化的风压力场可以分解为主坐标an(t)和本征模态(或协方差模态)φn(x，y)的组合，前者是时间随机函数，而后者是仅取决于空间坐标的确定性函数。

2 弯扭耦合颤振模型及表面压力波动特征

二元弹性悬挂弯扭耦合颤振风洞试验模型采用了经典的斜腹板箱形截面［10］，截面形状及尺寸如图1所示，系统重量为39.2kg。在斜腹板箱形截面上布置了180个同步测量的压力测点，测点非均匀布置，见图2。试验在均匀流场中进行，采样频率为312.5Hz，采样点数12000点，采样时间38.4s，位移采样频率为300Hz，采样时间为50s。试验共采集了6组颤振时的数据及5组模型固定时的数据，以反映测量数据的可重复性。

在零风速下，系统的竖弯及扭转振动频率分别为1.0997Hz及 2.2361Hz;竖弯及扭转阻尼比分别为0.62%及0.48%。在均匀流场中，弹性悬挂模型在风速为12.2m/s时发生颤振，颤振过程断面的扭转角变化时程如图3所示，相应的幅值谱如图4所示。图4显示结构发生颤振的频率是1.8695Hz，这个频率介于模型在零风速下竖弯频率和扭转频率之间。

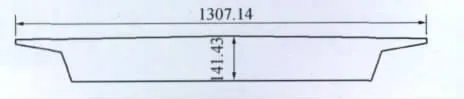
图1 模型截面图(单位:mm)Fig.1 Cross section of the scale section(unit:mm)

图2 模型压力测点布置图Fig.2 Distribution of measuring points

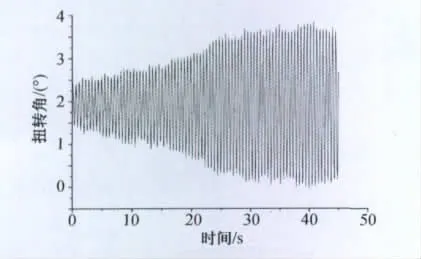
图3 模型颤振时扭转角随时间的变化(单位:°)Fig.3 Change of the torsion angle with time during fluttering(unit:°)

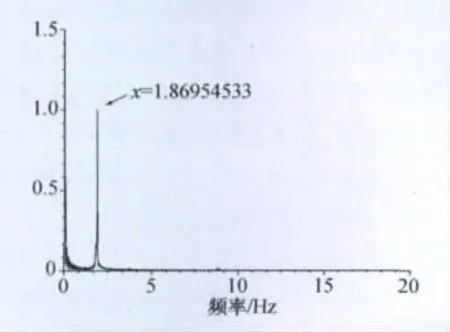
图4 模型颤振时扭转角时程幅值谱Fig.4 Amplitude spectrum of the torsion angle during fluttering

在整个颤振过程中，模型表面的归一化平均压力如图5所示(向外表示负压，向内表示正压，下同)。相应地，模型固定时，在12.2m/s的风速下，模型表面的平均压力如图6所示。可以看出，模型在颤振和固定的时候，表面的平均压力差别较小，只是颤振时上表面右侧的负压比模型固定时同一部位稍大。

图5 模型颤振过程中的平均表面压力Fig.5 Mean surface pressure during fluttering

图6 模型固定时的平均表面压力Fig.6 Mean surface pressure when fixed

为了明确模型表面各部分压力波动特征，将模型的表面轮廓线分成6部分:上甲板左部，上甲板右部，下腹板左部，下腹板右部，左斜腹板，右斜腹板。分别计算这六部分的压力对升力矩系数的贡献，并观察他们的相位差，结果如图7所示。

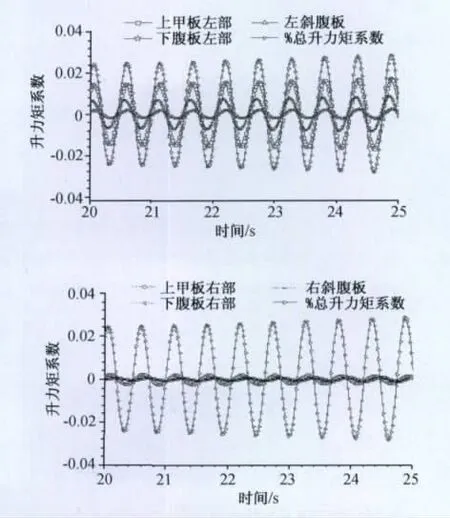
图7 总升力矩系数与各部分升力矩系数对比Fig.7 Comparison of the total and the single torque coefficient

图7显示，从幅值看，升力矩的波动主要是由上甲板及下腹板的左部压力主导，其次是左斜腹板和上甲板右部，贡献最小的是下腹板右部和右斜腹板。从相位上看，上甲板及下腹板的左部的相位和总升力矩系数的相位几乎相同，上甲板右部的相位稍稍落后一点，而下腹板右部和右斜腹板的相位与总升力矩相位相差几乎1/4个周期。颤振时模型各部分表面压力分布对升力矩系数的贡献如表1所示，其幅值谱如图8所示。从图8及表1同样可以看到，上甲板及下腹板的压力波动在总升力矩波动中占了绝大部分，有82%之多，它们是引发颤振形态的主动部分，而上甲板及下腹板的右部和右斜腹板虽然具有同样的卓越频率，但频率比较乱，幅值也较小，是受迎风侧特征湍流影响的被动区域，上甲板及下腹板右部和右斜腹板的相位落后于总升力矩时程相位也证明了这点。

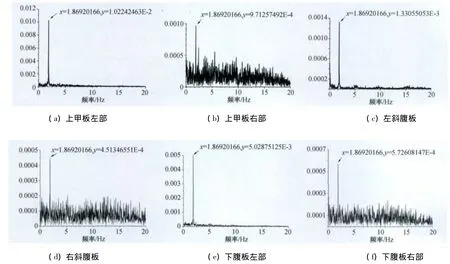
图8 表面各部分升力矩幅值谱Fig.8 Amplitude spectrums of torques in each part

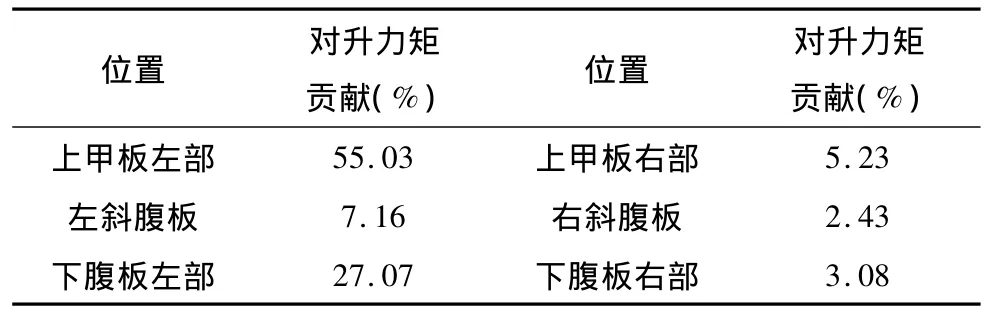
表1 颤振时模型各部分表面压力分布对升力矩系数的贡献Table 1 Contribution to the torque of each part

3 弯扭耦合颤振及固定时模型表面压力的POD分析

3.1 弯扭耦合颤振时模型表面压力POD分析

模型断面总共有180个测点，所以协方差矩阵为180×180的实对称阵，可以求解出180阶模态，而每一阶模态的主坐标就代表了该空间分布随时间的变化规律。由于颤振是单一频率的运动，所以对其表面压力进行POD分解时，只会有1阶或很少几阶模态与颤振运动联系紧密，我们取前七阶进行观察，后面的高阶模态所含的能量已经很少，不会对颤振运动产生很大影响。

颤振时模型表面压力前7阶本征模态φn(xi，yi)、主坐标an(t)时程及主坐标的幅值谱如图9所示。POD分解所获得的第一阶本征模态即为其平均压力分布，从上图9(a)可以看出，该分布与模型固定时的归一化平均压力分布(见图5)极其相似。

由图9(b)、图9(c)主坐标的时程可以看出，第2、3阶主坐标幅值随时间逐步变大，显示出发散的性质，其相应的幅值谱有明确的卓越频率(1.869Hz)，该频率与颤振频率一致，表明该本征模态与颤振时的断面发散性运动具有极强的关联性。图9(d)、图9(g)显示，第4～7阶主坐标幅值并不具有随时间逐步发散的性质，其相应的幅值谱也不存在明确的卓越频率。

根据式(5)，对每一阶本征模态所对应的压力分布进行积分就可以得到该本征模态对应的升力系数、升力矩系数和阻力系数。风洞试验显示该模型的颤振形态主要表现为有竖弯参与的扭转颤振形式，因此，我们关心由本征模态积分所获得的升力矩系数对总升力矩系数的贡献。图10(a)为总升力矩系数的幅值谱，图10(b～g)为第2～第7阶本征模态所对应的升力矩系数的幅值谱。表2为各阶本征模态对应的升力矩系数对总升力矩系数的贡献。从表2可以看出，第2阶本征模态对总升力矩系数波动的贡献占绝对主导地位，近96%。

以上分析显示，第二阶本征模态的主坐标的频率与颤振频率一致，且具有有振动位移一致的发散性，表明该本征模态与颤振时的断面发散性运动具有极强的关联性。第4～第7阶模态里面虽然都含有与颤振频率相同的频率，但随着模态数的增加，其他频率的成分也渐渐增加，第六阶模态以后，甚至颤振频率已经不是其主要频率，其模态特性渐渐变成模型本身外形导致的压力波动为主导。据此我们合理推断第二阶模态所代表的压力波动是引起结构颤振的原因，是颤振的主导模态，而其他本征模态为断面外形引起的特征紊流形成的结果。

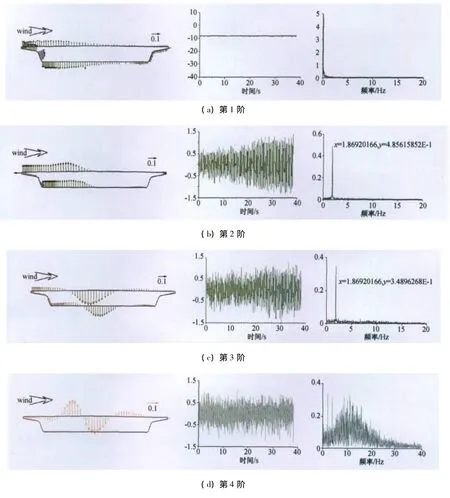
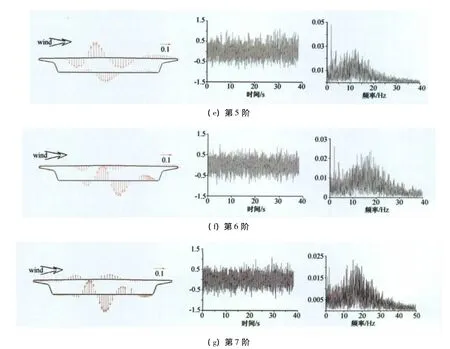
图9 本征模态、主坐标时程及主坐标幅值谱Fig.9 Intrinsic modes，the principal coordinate time-history and the amplitude spectrums

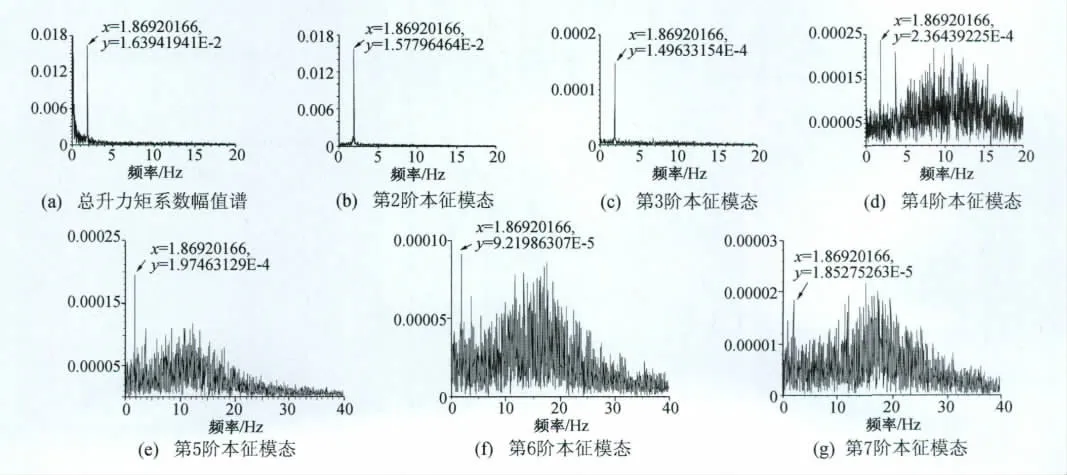
图10 颤振时的本征模态对应的升力矩的幅值谱图Fig.10 Amplitude spectrum of the torque corresponding to the intrinsic mode during fluttering

表2 模型颤振时POD分解第二至第七阶模态对升力矩系数的贡献Table 2 Contributions to the torque coefficient from the 2nd to 7th mode during fluttering

3.2 模型固定及颤振时表面压力对比分析

图11为模型颤振时的本征模态及固定时的本征模态对比图。图11显示，颤振时模型表面压力分布的第4阶本征模态与固定时模型的第4阶本征模态分布及幅值谱相似(图11b);颤振时的第5阶模态与固定时的第6阶模态分布及幅值谱相似(图11c);颤振时的第6阶本征模态与固定时的第3阶本征模态分布及幅值谱相似(图11d);颤振时的第7阶本征模态与固定时的第2阶本征模态分布及幅值谱相似(图11e)。只有颤振时的第2、3阶本征模态在固定模型时的表面压力分布的本征模态中找不到与之相近的。

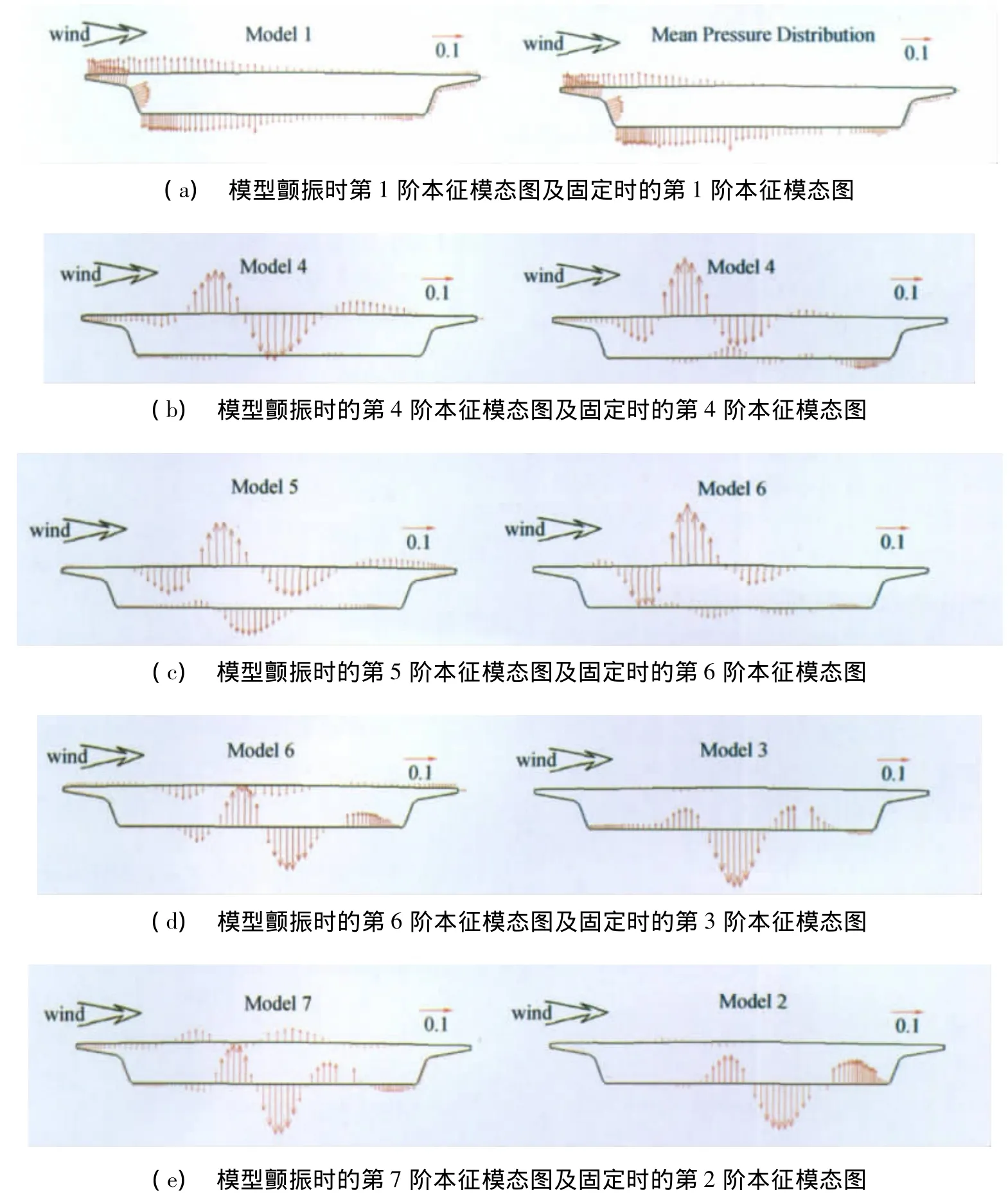
图11 模型颤振时的本征模态及固定时本征模态对比图Fig.11 The intrinsic mode during fluttering and the intrinsic mode in the static condition

图12 模型固定时的2～7阶本征模态主坐标幅值谱Fig.12 Amplitude spectrums of the principal coordinate from 2nd to 7th intrinsic mode in the static condition

4 小结

本文对弹性悬挂的刚体模型颤振时及固定时(来流风速一致)的表面压力进行采样。首先分析模型颤振时的表面压力分布特征，分析显示，主梁上甲板及下腹板左部的压力波动在总升力矩波动中占主导地位且频率与颤振频率一致，是引发颤振形态的主动部分，而右部是受迎风侧特征紊流影响的被动区域，其相位相对于左部具有滞后性。随后运用本征正交分解(POD)方法分析模型表面压力分布与颤振之间的关系。结果显示，所获得的本征模态中存在与颤振扭转发散运动关联极强的本征模态，该模态对总升力矩系数波动的贡献占绝对主导地位，其主坐标频率与颤振发散频率一致，且具有有振动位移一致的发散性，该模态在固定模型表面压力本征模态中找不到对应的模态。而其他模态主坐标幅值并不具有随时间逐步发散的性质，其相应的幅值谱也不存在明确的卓越频率。本文工作为今后颤振机理分析提供了一个新的思路与方法。

［1］SCANLAN R H.Airfoil and bridge deck flutter derivatives［J］.J.Eng.Mech.Div.，1997(6):1717-1737.

［2］WYATT T A，WALSHE D E.Bridge aerodynamics 50 years after the Tacoma Narrows-1:The Tacoma failure and after［J］.Journal of Wind Engineering and Industrail Aerodynamics，1992，40:317-326.

［3］杨詠昕.桥梁颤振机理研究及其应用［D］［博士学位论文］.同济大学，1998.

［4］Allan Larsen.Aerodynamics of the Tamoca Narrows Bridge-60 years later［R］.Structural Engineering International，2000:243-248，Hongkong.

［5］张伟，葛耀君.基于修正湍流冻结假设桥梁断面旋涡脱落分析［J］.同济大学学报(自然科学版)，2008，36(10):1307-1311.

［6］倪振华，江棹荣，谢壮宁.本征正交分解技术及其在预测屋盖风压场中的应用［J］.振动工程学报，2007，20(1).

［7］ARMITT J.Eigenvector analysis of pressure fluctuations on the West Burton instrumented cooling tower［R］.Central E-lectricity Research Labo ratories(U K)，Internal Report RD/L/N 114/68，1968.

［8］HOLMES J D.Analysis and synthesis of pressure fluctuations on bluff bodies using eigenvectors［J］.J.Wind Eng.Ind.Aerodyn，1990，33:219～230.

［9］BIENKIEWICZ B，TAMURA Y，HAM H J，UEDA H，HIBI K.Proper orthogonal decomposition and reconstruction of multi-channel roof pressure［J］.J.Wind Eng.Ind.Aerodyn.，1995，54/55:369 ～381.

［10］罗飞，杨文平，姚永龙.斜拉桥钢箱梁涡振性能风洞试验研究［J］.四川建筑，2005，25(1).