滑动蒙皮变后掠无人机非定常气动特性研究
陈 钱,白 鹏,陈 农,李 锋
(中国航天空气动力技术研究院,北京 100074)
0 引言
变形飞机是相对于传统固定外形飞机而言的一类新飞行器。随着飞行环境与任务的变化,变形飞机能如鸟类等飞行生物一样灵活改变自身形状与尺寸,获得实时最优性能。由于其仿生飞行特性[1-4]和空天应用前景[5-6],变形飞机引起 Cornell,Purdue 等二十所以上研究型大学的研究兴趣,受到NASA和DARPA等政府机构的投资重视,促成Lockheed Martin,NextGen Aeronautics等空天公司的持续参与,成为近年研究热点[7-18]。
已有的关于变形飞机的研究,可分为三类:小尺度局部变形、中尺度分布变形、大尺度全局变形。小尺度局部变形研究具有许多活跃的研究主题,如通过射流等方式实现“虚拟形状变化”[19-20],或通过柔性材料结构与精密作动装置等方式实现“实际形状变化”[21],从而对飞机局部流场结构产生有利影响,进而提高飞机性能。研究过程中,小尺度局部变形正越来越广泛地应用于实际飞行。探索更合适的小尺度局部变形方式(如鸟类羽毛微细结构在飞行时的主动变形[22]),是未来的研究趋势之一。中尺度分布变形研究是通过改变翼型弯度、厚度、弦长等方式,实现气动特性改进[23-24]和控制效率提升[25-26]。智能材料与结构研究的进展,使得中尺度分布变形越来越优于传统襟翼与副翼。未来的中尺度分布变形研究,将扩展变形的适用飞行范围以获得新的潜能[24]。大尺度全局变形研究中概念创新十分关键,如已有的折叠翼方案[15-16]和蝙蝠翼方案[17-18],均进行了全新概念设计,以便从根本上实现气动、结构、控制方面的显著收益。目前,通过地面测试、风洞实验、飞行演示验证,大尺度全局变形已经显示了巨大发展价值。在多学科交叉思路下,未来的大尺度全局变形研究将使变形飞机实现智能化[18]。
本文研究大尺度全局变形所引起的非定常气动问题。在飞机大尺度全局变形过程中,流场的内边界发生着大的变化,因而飞机的气动特性呈现出显著的非定常性;研究这种非定常性,对于更深入地理解变形飞机的气动特性和更可靠地控制变形飞机的仿生飞行,具有重要意义。在前期研究[27]中,通过变后掠变展长翼身组合体的气动特性近似理论分析、数值模拟和风洞实验,初步认识了变形过程中的准定常气动特性并探索了变形过程中的非定常气动特性;本文基于“滑动蒙皮变后掠无人机”这一更新的“可变形飞行器大尺度全局变形研究平台”,进一步探索变形过程中的非定常气动特性。
1 滑动蒙皮变后掠无人机概念原理
本文研究对象为变后掠无人机。无人机为鸭式布局,主翼分为两段,内段外形固定,外段后掠角可双向变化;另外,主翼外段翼尖置有垂直尾翼。图1给出了无人机变后掠过程中主翼外段处于两种典型后掠角时全机的平面投影。
为了实现无人机的大尺度变后掠,主翼外段经过了特别设计:主翼外段包括三部分结构,分别为能绕固定点转动的前缘、能进行“可控错动”的平行四边形中间结构、能绕固定点转动的后缘,其中,前缘与后缘均具有刚性型面,而中间结构则由翼肋、桁条、柔性蒙皮构成。为了使变形过程中无人机始终保持较规范气动外形,前缘和后缘与主翼内段交界处均设计了小型刚性件。
上述中间结构在“可控错动”过程中,各翼肋始终与机身轴线平行,各桁条则分别绕内侧端点旋转,而柔性蒙皮则发生“滑动”的剪切式变形,因而本文将这种变后掠无人机称为“滑动蒙皮变后掠无人机”。

图1 主翼外段后掠角可变的变后掠无人机Fig.1 Variable-sweep unmanned aerial vehicle with wing outboard section morphing
2 变后掠非定常气动特性实验测试
依据上述概念原理,研制了带有闭环控制系统的滑动蒙皮变后掠无人机风洞实验模型。模型机身长1.101 m,最大展长1.910m。模型主翼外段由置于主翼内段的电动推杆驱动。主翼外段的每一后掠角对应着电动推杆的某一伸长量,电动推杆的每一伸长量对应着电动推杆内电阻元件的某一电阻值,因而,当控制系统测得电动推杆内电阻元件的电阻值时,即可计算出主翼外段的后掠角,从而将这一后掠角值用于变后掠过程的闭环控制。闭环控制主要由控制器来完成。控制器能与计算机软件进行通信以获取初始指令,能控制电动推杆的转/停,能从电动推杆获得电阻元件的电阻值并计算出主翼外段的后掠角值用于闭环控制。所有控制信号线均采用屏蔽线,并与电源线一起从实验模型尾部引出。
实验风洞为单回流闭口低速风洞,实验段长14m,横截面为3m×3m的四角圆化正方形,圆角半径0.5m,有效横截面积8.7854m2。空风洞最高风速100m/s,风洞湍流度低于0.13%,风洞内壁上、下各有0.2°扩张角,以消除沿壁面的边界层增长的影响,并基本消除实验段轴向静压力梯度。气动力与力矩测量采用N6YT19#内式六分量应变天平。实验中风速为25m/s。
实验模型后掠角变化规律包括两种,一是三角函数规律:
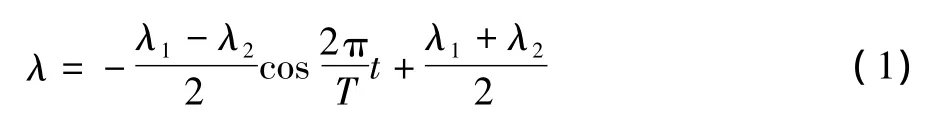
式中,λ为t时刻后掠角,λ1为最小后掠角,λ2为最大后掠角,T为运动周期。二是周期线性函数规律:
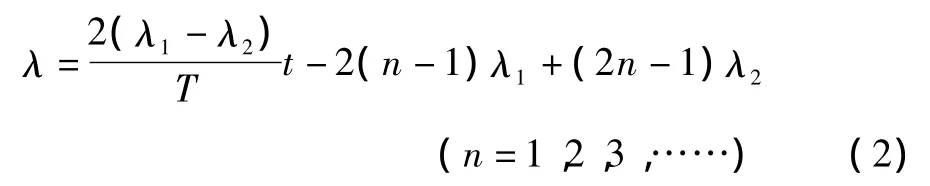
式中,n为运动周期数,其它符号意义同上。
实验模型后掠角变化速率包括三种,分别对应T的三种取值。
变形飞机气动特性测试相比于传统固定外形飞机气动特性测试,在实验数据采集与处理方面具有诸多差异。本小组根据前期研究[27],获得了这些差异的具体特点,并针对这些特点,设计了相应的实验方法,详见文献。
3 结果分析
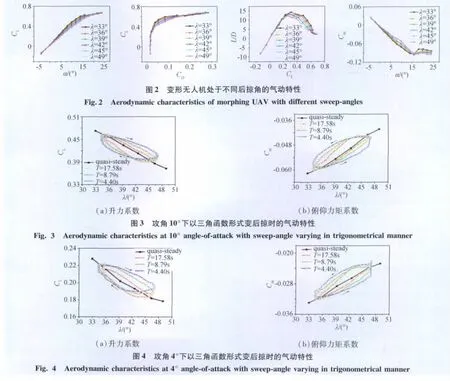
在研究变后掠无人机变形过程中的非定常气动特性之前,有必要对其准定常气动特性进行研究,以便对后掠角的影响形成预先认知。图2显示了变后掠无人机处于不同后掠角时的气动特性。图2(a)表明,在失速前的正攻角时,升力随后掠角增大而减小,且后掠角增大能延迟失速。图2(b)表明,不同外形的阻力极曲线族所形成的包线,范围大于任一单独外形的阻力极曲线所形成的包线,因而对于任一给定升力,变后掠无人机可以通过采用适当外形来达到实时最优阻力。图2(c)表明,在升力系数为0.5附近,外形改变能使升阻比改变80%以上,预示着变形技术在气动效率改进方面的巨大潜力。图2(d)表明,变形前后无人机均处于静稳定状态。
变后掠过程中,无人机气动特性会与上述准定常结果呈现何种差异,是亟待回答的问题。为此,首先选取一典型攻角,研究了此攻角下无人机气动特性随后掠角连续变化的规律。
图3显示了10°攻角下,后掠角按(1)式变形规律以不同运动周期进行变形时,一个周期内升力系数和俯仰力矩系数随后掠角的变化,并与定态实验的准定常结果进行了比较。
从图3(a、b)均可见,非定常结果与准定常结果存在显著差异。定性的具体表现为:1)后掠角往复变化的一个周期内,非定常升力系数曲线在准定常升力系数曲线周围形成滞回环;2)变后掠越快(即运动周期越短),滞回环越大。定量的具体表现为:无人机以约7.5°/s的速率变后掠,会使非定常气动特性数值偏离其相应的准定常数值5%以上。进一步观察图3(a、b)可见,非定常升力系数的滞回环呈顺时针方向,俯仰力矩系数的滞回环呈逆时针方向,即:后掠角增大时,非定常升力系数趋向于大于准定常升力系数,而俯仰力矩系数趋向于小于准定常俯仰力矩系数;后掠角减小时,规律与之相反。在分析上述观察所得规律的产生原因之前,有必要考虑另一个问题,即:这些规律是具有一定普适性的,还是具有一定偶然性的。为此,选取另一典型攻角,同样研究了此攻角下无人机气动特性随后掠角连续变化的规律。
图4显示了4°攻角下,后掠角按(1)式变形规律以不同运动周期T进行变形时,一个周期内升力系数和俯仰力矩系数随后掠角的变化,并与定态实验的准定常结果进行了比较。可见,10°攻角下变后掠时观察得到的上述规律在4°攻角下变后掠时同样成立。
既然上述规律具有一定的普适性,那么,以下对其成因进行初步分析,而详细成因将在后续工作中予以进一步研究。
对于“滞回环形式的非定常气动特性”,成因可能在于变后掠引起的流场结构迟滞。图9比较了后掠角时变规律与升力系数时变规律,其中三幅子图分别表示三种不同变后掠速率的情形。从任一幅子图均可见,升力系数开始显著变化的时刻明显滞后于后掠角开始显著变化的时刻。气动特性上的这种滞后可能源于流场结构上的迟滞,因为变后掠过程中流场边界连续变化,而相应的流场结构变化可能慢于流场边界变化。
对于“变后掠越快滞回环越大”,成因包括多个方面。第一方面,从图5三幅子图可见“升力系数开始显著变化的时刻”相对于“后掠角开始显著变化的时刻”的滞后量,因变后掠速率不同而不同;变后掠越快,滞后量越小(这里应注意到,图5三幅子图的横坐标刻度不同);这似乎会引起“变后掠越快滞回环越小”。然而,另一方面的情况是,时间轴上的滞后量换算到后掠角轴上的滞后量时,变后掠速率越大则滞后量被“放大”的“倍数”越大。由此可推断,本文实验中,第二个方面占优,因而出现的现实是“变后掠越快滞回环越大”。
对于“升力系数与俯仰力矩系数二者滞回环方向相反”,成因在于压心在力矩参考点之后,俯仰力矩为负值,即俯仰力矩为低头力矩。
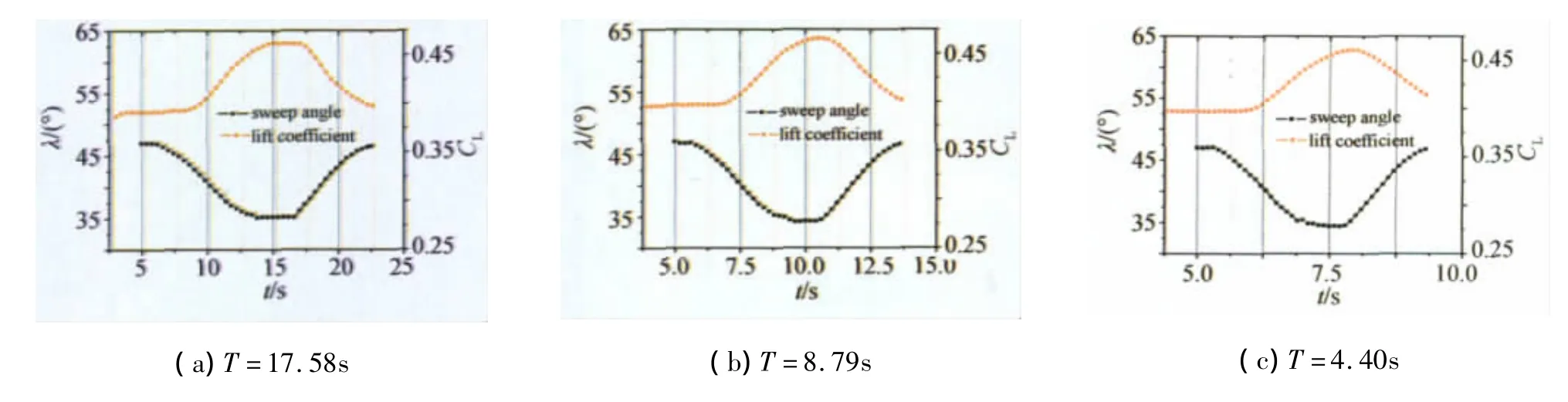
图5 后掠角与气动特性随时间的变化Fig.5 Variation of sweep-angle and aerodynamic characteristics with time
另外,可对变后掠引起的“机翼附加速度”进行考察。无人机的主翼外段变后掠时,其相对于远场来流的速度发生变化,这将使非定常气动特性(如升力)的数值产生较大变化,这似乎是非定常气动特性与准定常气动特性产生显著差异的原因之一。在定量近似分析了这种原因的可能性之后,发现本文实验参数条件下,“机翼附加速度”与远场来流速度相比极小,因而可忽略这一原因。后续研究可针对一般意义上的变后掠,合理选取多组计算或实验参数,对这一原因继续探讨。
在实验模型设计过程中,还构建了另一变后掠运动规律,即式(2)的周期线性函数规律。图6显示了10°攻角下,后掠角按式(2)变形规律进行变形时,一个周期内升力系数和俯仰力矩系数随后掠角的变化,并与定态实验的准定常结果进行了比较。可见,上述结论对此情形同样成立。
上文指出,无人机以约7.5°/s的速率变后掠,会使非定常气动特性数值偏离其相应的准定常数值5%以上。这一较大偏离,表明了研究变后掠过程中非定常气动特性的意义,也对变形过程中的飞行控制提出了较高要求。后续研究将更多采用定量视角,对变后掠过程中的非定常气动特性予以探讨。
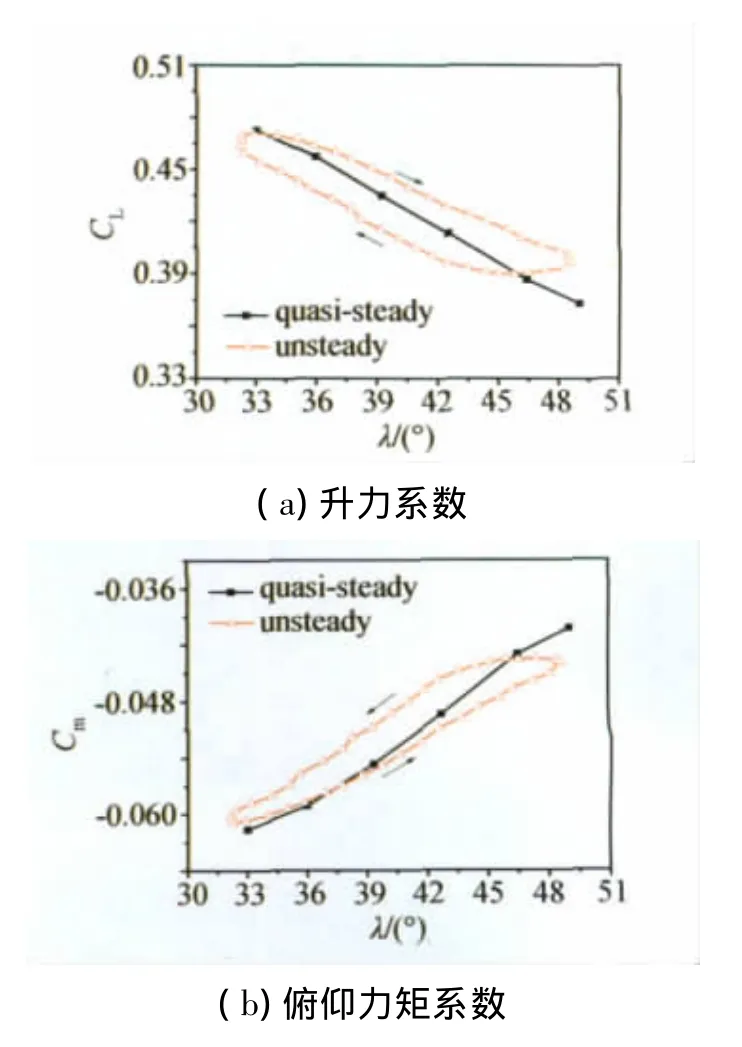
图6 10°攻角下以周期线性函数变后掠时的气动特性Fig.6 Aerodynamic characteristics in 10°angle-of-attack with sweep-angle varying in linear manner
4 结论
通过变后掠无人机的风洞实验研究,探索了变形过程中在非定常气动力方面的特性及其产生原因,得到以下主要结论:
(1)变后掠过程中的非定常气动特性与相应的准定常气动特性显著不同。非定常气动特性曲线在相应的准定常曲线周围形成滞回环;变后掠速率越快,滞回效应越显著;
(2)当无人机主翼外段以约7.5°/s的速率变后掠时,非定常气动特性数值偏离相应的准定常数值达5%以上,表明了工程设计中应对变后掠过程中的非定常气动特性予以重视;
(3)变后掠无人机非定常气动特性产生的主要原因可能在于流场结构迟滞和机翼附加速度。
对于变后掠过程中非定常气动特性影响因素和物理机制的全面探讨,将是后续研究中的重要内容。
[1]WOLF M,JOHANSSON L C,von BUSSE R,et al.Kinematics of flight and the relationship to the vortex wake of a Pallas'long tongued bat(Glossophaga soricina)[J].The Journal of Experimental Biology,2010,213(12):2142-2153.
[2]HEDENSTRÖM A,JOHANSSON L C,WOLF M,et al..Bat flight generates complex aerodynamic tracks[J].Science,2007,316(5826):894-897.
[3]HENNINGSSON P,SPEDDING G R,HEDENSTRÖM A.Vortex wake and flight kinematics of a swift in cruising flight in a wind tunnel[J].The Journal of Experimental Biology,2008,211(5):717-730.
[4]LENTINK D,MÜLLER U K,STAMHUIS E J,et al.How swifts control their glide performance with morphing wings?[J].Nature,2007,446(7139):1082-1085.
[5]WEISSHAAR T.Morphing aircraft technology -new shapes for aircraft design[A].Meeting Proceedings RTO-MP-AVT-141[C].Neuilly-sur-Seine,France:RTO,2006:O1-1-O1-20.
[6]CLERY D.Aircraft designers shoot for savings on the wing[J].Science,2009,325(5942):810.
[7]SECANELL M,SULEMAN A,GAMBOA P.Design of a morphing airfoil using aerodynamic shape optimization[J].AIAA Journal,2006,44(7):1550-1562.
[8]GAMBOA P,VALE J,LAU F J P,SULEMAN A.Optimization of a morphing wing based on coupled aerodynamic and structural constraints[J].AIAA Journal,2009,47(9):2087-2103.
[9]NAMGOONG H,CROSSLEY W A,LYRINTZIS A S.Aerodynamic optimization of a morphing airfoil using energy as an objective[J].AIAA Journal,2007,45(9):2113-2124.
[10]MAUTE K,REICH G W.Integrated multidisciplinary topology optimization approach to adaptive wing design[J].Journal of Aircraft,2006,43(1):253-263.
[11]POPOV A V,BOTEZ R M,LABIB M.Transition point detection from the surface pressure distribution for controller design[J].Journal of Aircraft,2008,45(1):23-28.
[12]POPOV A V,GRIGORIE T L,BOTEZ R M,et al.Modeling and testing of a morphing wing in open-loop architecture[J].Journal of Aircraft,2010,47(3):917-923.
[13]SEIGLER T M,NEAL D A,BAE J S,INMAN D J.Modeling and flight control of large-scale morphing aircraft[J].Journal of Aircraft,2007,44(4):1077-1087.
[14]SEIGLER T M,NEAL D A.Analysis of transition stability for morphing aircraft[J].Journal of Guidance Control and Dynamics,2009,32(6):1947-1954.
[15]IVANCO T G,SCOTT R C,LOVE M H,et al.Validation of the lockheed martin morphing concept with wind tunnel testing[R].AIAA-2007-2235,2007.
[16]BALDELLI D H,LEE D H,PEÑA L S,HOPPER D,CANNON B.Practical modeling,control and simulation of an aeroelastic morphing UAV [R]. AIAA-2007-2236,2007.
[17]BOWMAN J,SANDERS B,CANNON B,et al.Development of next generation morphing aircraft structures[R].AIAA-2007-1730,2007.
[18]GANDHI N,COOPER J,WARD D,et al.A hardware demonstration of an integrated adaptive wing shape and flight control law for morphing aircraft[R].AIAA-2009-5890,2009.
[19]DEB D,TAO G,BURKHOLDER J O,SMITH D R.Adaptive compensation control of synthetic jet actuator arrays for airfoil virtual shaping[J].AIAA Journal,2007,44(2):616-626.
[20]CHEN F J,BEELER G B.Virtual shaping of a two-dimensional NACA 0015 airfoil using synthetic jet actuator[R].AIAA-2002-3273,2002.
[21]COUTU D,BREILOVSKI V,TERRIAULT P.Promising benefits of an active-extrados morphing laminar wing[J].Journal of Aircraft,2009,46(2):730-731.
[22]BACHMANN T,KLÄN S,BAUMGARTNER W,et al.Morphometric characterisation of wing feathers of the barn owl(Tyto alba pratincola)and the pigeon(Columba livia)[J].Frontiers in Zoology,2007,4:23-37.
[23]陈钱,白鹏,尹维龙,冷劲松,詹慧玲,刘子强.可连续光滑偏转后缘的变弯度翼型气动特性分析[J].空气动力学学报,2010,28(1):46-53.(CHEN Q,BAI P,YIN W L,et al.Analysis on the aerodynamic characteristics of variable camber airfoils with continuous smooth morphing trailing edge[J].ACTA Aerodynamica Sinica,2010,28(1):46-53.)
[24]POGGIE J,TILMANN C,FLICK P,et al.Closed-loop stall control on a morphing airfoil using hot-film sensors and DBD actuators[R].AIAA-2010-0547,2010.
[25]PENDLETON E,FLICK P,PAUL D,et al.The X-53 a summary of the active aeroelastic wing flight research program[R].AIAA-2007-1855,2007.
[26]KUDVA J.Overview of the DARPA smart wing project[J].Journal of Intelligent Material System and Structure,2004,15(4):261-267.
[27]陈钱,尹维龙,白鹏,冷劲松,刘子强.变后掠变展长翼身组合体系统设计与特性分析[J].航空学报,2010,31(3):606-613.(CHEN Q,YIN W L,BAI P,LENG J S,LIU Z Q.System design and characteristics analysis of a variable-sweep and variable-span wing-body[J].ACTA Aeronautica et Astronautica Sinica,2010,31(3):606-613.)

