高阶间断有限元法的并行计算研究
夏轶栋,伍贻兆,吕宏强,宋江勇
(1.南京航空航天大学航空宇航学院,江苏南京 210016;2.中国飞行试验研究院,陕西西安 710089)
0 引言
间断有限元法[1-3]在 1973 年由 Lesaint和 Raviart[4-5]首先提出,后经 Cockburn 和 Shu[6-8]等逐步发展。在当今计算流体力学领域,间断有限元法由于集合了传统有限元法和有限体积法的特点而成为目前科学计算领域的研究热点之一[9-11]。在单元内部,间断有限元法跟传统有限元法一样用高阶多项式来提高精度。而在单元的边界处,间断有限元法又可以方便地采用有限体积法中的思路来基于Riemann问题构造数值通量[5,12],以此来实现逆风格式。
高阶间断有限元法应用上的瓶颈之一为计算效率问题[13]。由于在相同的网格上相对于有限体积法包含更多未知变量,这种方法需要庞大的存储空间,且计算时间较长。在串行计算机上,这种局限对于大型问题和高精度求解尤为突出。因此为实现高阶间断有限元法的高效性,引入并行计算势在必行。
本文根据间断有限元法的数据结构,基于METIS网格分区技术,设计了并行计算策略,实现了高阶间断有限元法并行计算程序。在非结构网格上对二维Euler方程的亚声速情况进行了数值模拟实验,并对其加速比和并行效率进行分析。在程序设计中,采用动态内存分配合理使用有限存储空间。经与串行计算结果对比,本文的高阶间断有限元法并行计算程序得到了较好的加速比和并行效率。这使得采用高阶间断有限元法计算更为复杂的问题成为可能。
1 间断有限元法数值离散
守恒型Euler方程
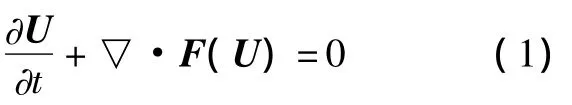
式(1)两边乘测试函数V,并在计算域内积分,运用分部积分后,弱解形式为
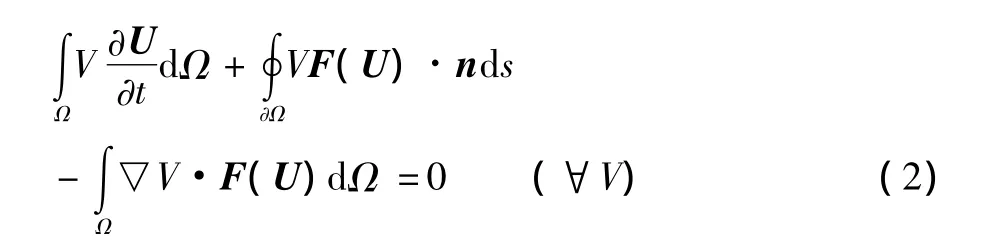
式中:Ω为计算域;∂Ω为Ω的边界。
将计算域划分为网格{e},其中e表示网格单元。在每个单元内:
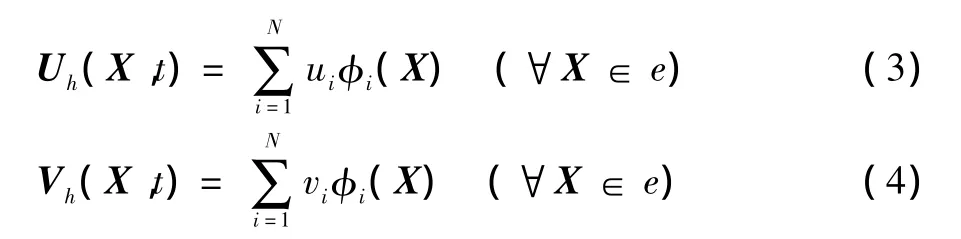
式中φi(X)为基函数。将式(3、4)代入式(2),得:
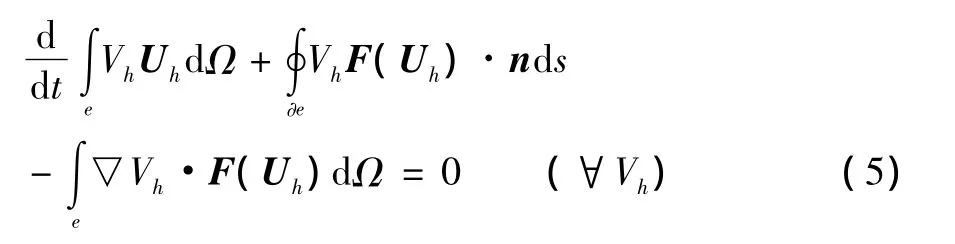
式中∂e为单元e的边界。式(5)必须对于任何单元和任何Vh都满足。而在每个单元内部,Vh是N个基函数的线性组合,因此式(5)可写为:
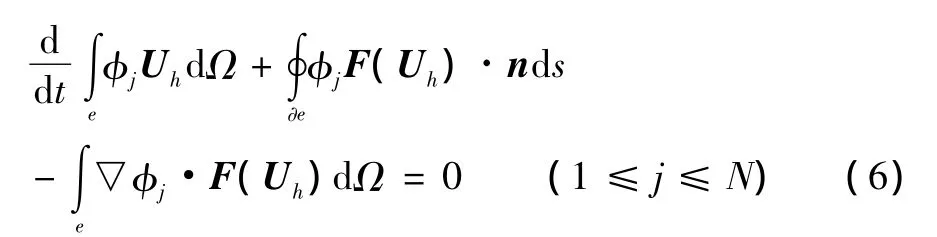
式(6)称为p阶间断有限元离散[9],p为式(3)和式(4)中基函数的最大阶数。
2 分区并行计算方法
2.1 网格分区和边界处理
高阶间断有限元法的数据结构特点是,每个网格单元流场信息的计算只涉及其相邻单元。为实现其并行计算,使用软件METIS对网格进行分区,将全局网格划分为若干局域网格,局域网格之间的数据仅与相邻局域网格分区边界上的单元有关。METIS划分的局域网格具有相近的单元数,可以保证多进程并行计算的负载平衡。
在物面和远场分别采用无穿透和无反射边界条件。对于网格分区所产生的分区边界,通过引入虚拟网格单元的方法解决(如图1所示)。1号局域网格的虚拟单元(用●表示)与2号局域网格分区边界上的单元(用■表示)相对应;2号局域网格的虚拟单元(用●表示)与1号局域网格分区边界上的单元(用■表示)相对应。因此虚拟单元的所有流场数据均来自其对应相邻局域网格分区边界上的单元,只需通过计算进程间的数据传递得到。本文的数据传递方法基于MPI。
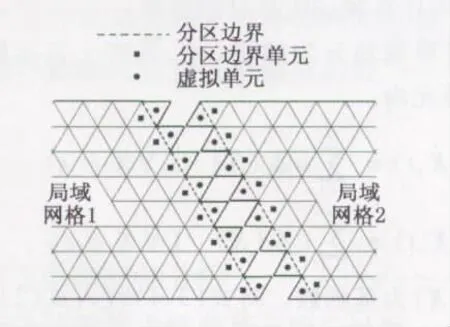
图1 分区边界示意图Fig.1 Illustration of partition boundary
2.2 并行策略设计与实现
直接采用有限体积方法在单元边界处定义数值通量[9],即式(6)中的通量函数F(Uh)·n用数值通量函数H(U-,U+,n)来代替,其中 U-和 U+分别表示该单元变量和其相邻单元的变量,单元Ωe的流场信息的求解只与相邻单元相关。本文采用Local Lax-Friedrichs(LLF)格式计算数值通量。
式(6)最终的离散形式可写为:

式中:u为向量,包含式(4)中的所有未知变量;M为质量矩阵;R(u)为残值。
对式(7)的求解,本文采用的是牛顿-块高斯赛德尔法(Newton-Block GS),即:

式中:C∈[0,1]。△u通过求解以下线性方程

获得。△u的形式如下:
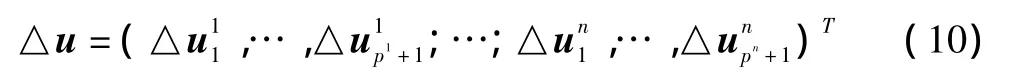
上述线性方程式(9)的数据结构非常适合并行:△u中向量按单元序号依次排列,单元Ωi的△ui求解只与相邻单元有关,∂R/∂u 是稀疏块矩阵[14-16]。因此在块矩阵∂R/∂u的第i行中,只有第i列块矩阵和与第i号单元相邻的单元所对应的块矩阵为非零矩阵。
针对式(9)的数据结构,设计了并行的 Newton-Block GS迭代策略。在每次分区并行Newton迭代中,首先分配动态空间,将上一次Block GS迭代后各局域网格分区边界上的单元△u新值传递给相邻局域网格的虚拟单元,作为相邻局域网格分区边界单元的本次Block GS迭代的旧值,最后释放动态空间。各进程按上述规则同步传递数据,并通过迭代直至收敛,进入下一次Newton迭代。
另外,在求解 H(U-,U+,n)前,将本次 Newton迭代时局域网格分区边界上U-新值传递给其相邻局域网格的虚拟单元,作为其相邻局域网格分区边界上单元的U+新值。各计算进程在每次Newton迭代后需将所有局域网格上求得的残值R(u)经传递后求和,同时判断是否收敛。图2为多进程并行计算的牛顿法迭代流程。
3 并行计算数值结果与性能分析
3.1 NACA0012翼型绕流问题数值模拟
并行计算环境应用MPICH2,建立在lenovo R510计算机工作站(双四核Xeon 5310处理器,内存8Gb),程序采用C++语言编写。
使用单元数为800的二维非结构网格。来流马赫数Ma和迎角α分别取为0.63和2°。利用上述介绍的并行算法对NACA0012翼型绕流问题进行数值模拟。首先用串行程序计算,然后将全局网格划分为2个、4个和8个局域网格分别进行并行计算,并给出数值结果。
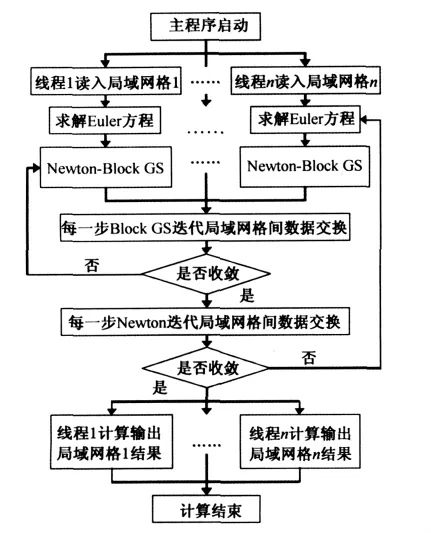
图2 牛顿法迭代流程图Fig.2 Flowchart of Newtown iteration
图3给出了NACA0012翼型非结构网格的8分区示意图。图中,粗线为局域分区边界。局域网格的单元个数分别为 102,100,101,98,100,99,98,102。
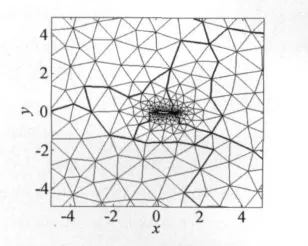
图3 NACA0012翼型8分区网格Fig.3 8 partition grids of NACA0012 airfoil
将串行计算结构和8分区并行计算结果进行比较。图4给出了p=4的等马赫线图。上图为串行计算所得,下图为8分区并行计算所得。通过比较,流场等马赫线图高度吻合。
图5为翼型上下表面压力系数分布。上为p=4的并行计算结果与串行计算结果比较,曲线完全重合。下为并行计算p=0~4时得到的翼型上下表面压力系数分布,可见高阶情况下的精度提高效果非常明显。
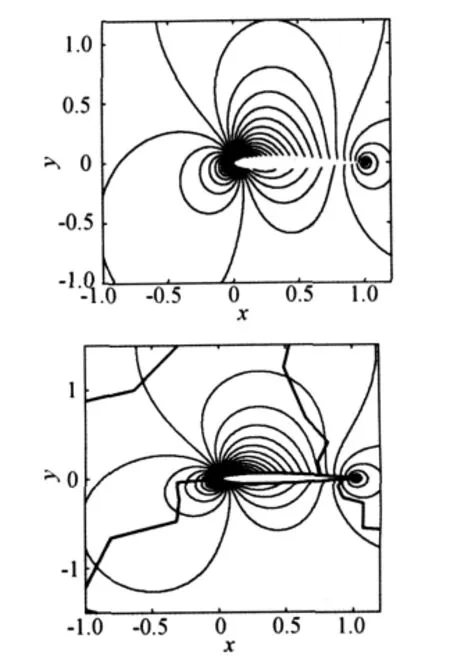
图4 亚声速下NACA0012翼型绕流等马赫线图(Ma=0.63,α =2°)Fig.4 Mach isolines around NACA0012 airfoil(Ma=0.63,α =2°)
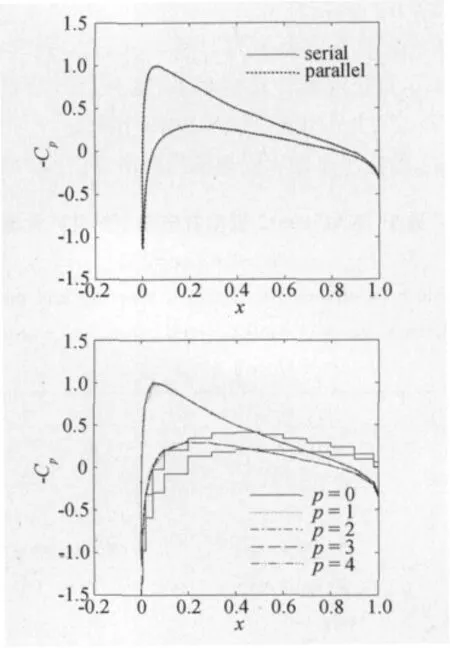
图5 NACA0012翼型压力系数分布(Ma=0.63,α=2°)Fig.5 Distribution around NACA0012 airfoil(Ma=0.63,α =2°)
图6对并行计算和串行计算的数值模拟收敛过程进行比较,其中横坐标为Newton迭代步数,纵坐标为残值R。结果表明:两者残值曲线重合。p=0时以给定的初始解为远场来流,经16步Newton迭代后残值降到10-10以下,然后以此收敛解作为p=1时的初始解,经12步迭代后残值降到10-10以下。最后当p=4时经9步迭代后达到收敛。上述比较验证了高阶间断有限元法并行计算的正确性,同时表明,Newton-Block GS法具有快速收敛和迭代效率高的优点。
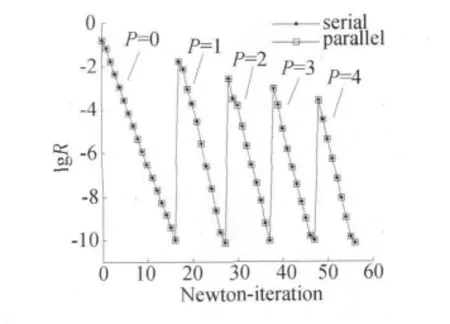
图6 NACA0012翼型数值模拟的收敛过程(Ma=0.63,α =2°)Fig.6 Convergence history of NACA0012 airfoil numerical simulation(Ma=0.63,α =2°)
3.2 并行算法性能分析
衡量并行算法性能的主要指标是并行加速比和并行效率。设Ts为串行程序计算时间,Tp为并行程序计算时间,n为处理器计算进程数,则并行计算的加速比为S=Ts/Tp,并行效率为E=S/n×100%。
表1给出了采用不同规模的网格,对上述NACA0012翼型绕流问题进行数值模拟的并行性能分析。第一行数据1、2、4、8表示划分局域网格的个数即采用处理器的核数。
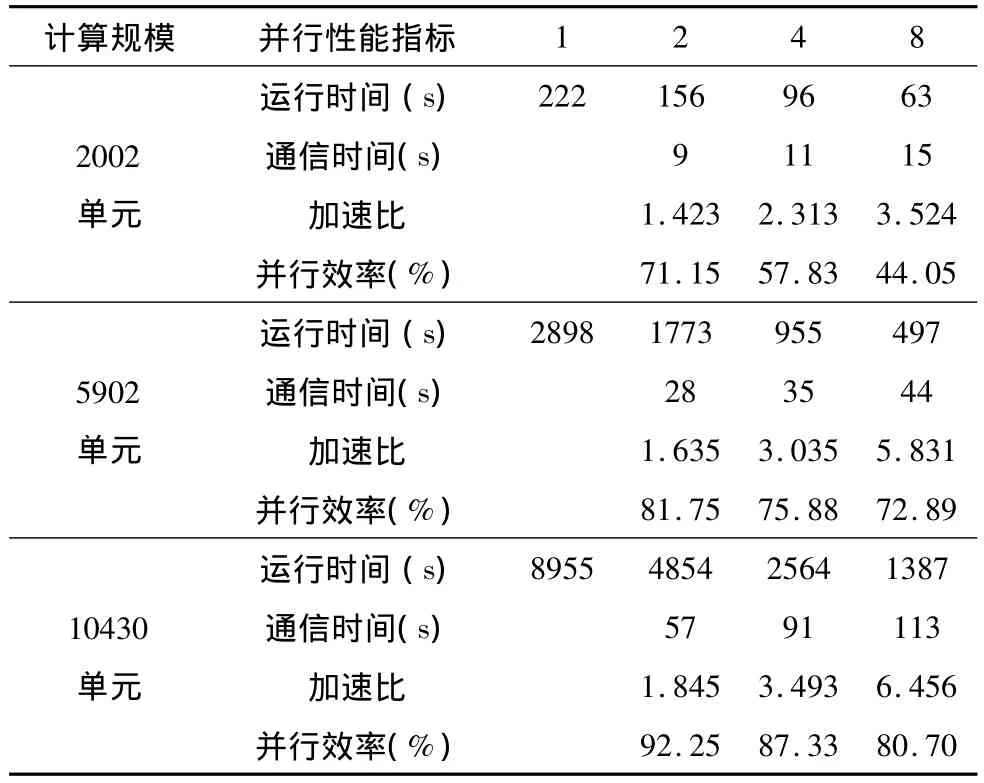
表1 NACA0012翼型数值模拟的并行性能(Ma=0.63,α =2°)Table 1 Convergence timings,speedup and parallel efficiency for NACA0012 airfoil numerical simulation(Ma=0.63,α =2°)
通过数据分析可以得出,当处理器核数一定时,随着计算规模的增大,数据通信时间TM在整体计算时间中所占比例降低,加速比和并行效率都有所提高。
另外,当求解问题的计算规模一定时,随着处理器数核数的增加,尽管加速比有所提高,但各处理器间的总数据通信时间所占总计算时间比例增加,因此并行效率逐步降低。
4 结论
本文实现了非结构网格上高阶间断有限元法的并行计算。实验表明,该方法的并行求解具有收敛快、精度高以及大幅节省计算时间的特点。这使得采用高阶间断有限元法处理更复杂问题时,在保证高精度解的同时,能够有效缩短计算时间。
另外,本文设计的高阶间断有限元法的并行计算策略可直接推广到Navier-Stokes方程和三维情况中去。这方面的研究工作目前正在进行中。
[1]LIN S Y,CHIN Y S.Discontinuous Galerkin finite element method for Euler and Navier-Stokes equations[J].AIAA Journal,1993:2016-2023.
[2]BASSI F,RRBAY S.High-order accurate discontinuous finite element solution of the 2D Euler equations[J].Journal of Computational Physics,1997,138(2):251-285.
[3]RASETARINERA P,HUSSAINI M Y.An efficient implicit discontinuous spectral Galerkin method[J].Journal of Computational Physics,2001:718-738.
[4]LESAINT P.Sur la resolution des systemes hyperboliques du premier order par des methods delements finis[D].Unversite Paris 6,1975.
[5]LESAINT P,RAVIART P A.On a finite element method to solve the neutron transport equation[M].//C.de Boor.Mathematical Aspects of Finite Elements in Partial Differential Equations.Academic Press,New York,1974.
[6]COCKBUTRN B,HOU S,SHU C W.TVD Runge-Kutta local projection discontinuous Galerkin finite element method for conservation lawsⅡ:general framework[J].Mathematics of Computation,1989:52-411.
[7]COCKBUTRN B,HOU S,SHU C W.TVD Runge-Kutta local projection discontinuous Galerkin finite element method for conservation lawsⅢ:one dimensional systems[J].Journal of Computational Physics,1989:84-90.
[8]COCKBUTRN B,HOU S,SHU C W.TVD Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws IV:the multidimensional case[J].Mathematics of Computation,1990:45-581.
[9]吕宏强,伍贻兆,周春华,等.稀疏非结构网格上的亚声速流高精度数值模拟[J].航空学报,2009,30(2):200-204.
[10]贺立新,张来平,张涵信,等.任意单元间断Galerkin有限元计算方法研究[J].空气动力学学报,2007,25(2):157-162.
[11]贺立新,张来平,张涵信,等.间断Galerkin有限元和有限体积混合计算方法研究[J].力学学报,2007,39(1):15-22.
[12]COCKBURN B,KAMIADAKIS G E,SHU C W.Discontinuous Galerkin methods:theory,computation and applications[M].Berlin:Springer,1999.
[13]LUO H,BAUM J D,LOHNER R.A p-multigrid discontinuous Galerkin method for the Euler equations on unstructured grids[J].Journal of Computational Physics,2006,211(2):767-783.
[14]LU H Q.High-order finite element solution of elastohydrodynamic lubrication problems[D].Leeds,UK:University of Leeds,2006.
[15]HARTMANN R.Adaptive finite element methods for the compressible Euler equations[D].Heidelberg,Germany:University of Heidelberg,2002.
[16]LU H Q,BERZINS M,GOODYER C E,et al.High order discontinuous Galerkin method for elastohydrodynamic lubrication line contact problems[J].Communications in Numerical Methods in Engineering,2005,21(11):643-650.

