覆冰导线气动力特性风洞试验研究

王 昕，楼文娟，沈国辉，许福友

(1.浙江大学结构工程研究所，浙江杭州 310058;2.大连理工大学建设工程学部，山东大连 116024)

0 引言

输电线路舞动是导线低频率、大幅度的自激振动，通常发生在冬季雨雪冰冻天气导线覆冰而形成非圆断面的情况下。舞动将使导线承受额外的动态张拉力，并造成输电系统相间闪络、电弧烧伤、金具损坏，严重时可导致整条线路跳闸停电、断线倒塔等事故。

输电线路的舞动机理是国内外学者所长期研究的问题。Den Hartog最早于20世纪30年代提出了单自由度竖向舞动机理［1］，认为覆冰截面的气动升力负斜率幅值大于气动阻力时，导线竖向运动失稳引发舞动;Nigol增加了对扭转自由度的考虑，提出当覆冰导线气动扭转阻尼为负时且幅值超过导线固有阻尼时将激发扭转失稳，若线路扭转频率与竖向运动频率接近则将进一步产生扭转-竖向耦合失稳，即扭转舞动机理［2］;Yu等考虑了导线覆冰的偏心耦合效应，提出了偏心惯性耦合失稳机理［3］，即由于覆冰偏心惯性引起攻角变化，使得相应的升力对横向振动形成正反馈，最终形成大幅度舞动。对以上机理而言，覆冰导线气动力特性是输电线路舞动的核心参数，因而获取各种覆冰导线的气动力系数是研究输电线路舞动以及防舞的基础性工作。

Nigol和Keutgen分别在风洞中利用天平测量了新月形断面覆冰导线的气动力系数［4－5］;Stumpf则对D形断面覆冰导线的气动力特性进行了风洞试验研究［6］;Chadha等同样通过风洞获取了三种新月形断面和一种D形断面覆冰导线在各自部分风攻角下的气动力系数［7］;李万平和Shimizu则均针对新月形覆冰分裂导线展开研究，分别得到了三分裂及四分裂新月形覆冰导线的气动力系数试验值［8－9］;此外，李万平还针对特大厚度覆冰导线发生驰振时的实际冰形断面进行了风洞试验研究［10］。但以上试验通常在均匀流场中进行，而实际线路所处地形情况复杂，经过输电导线的气流必然存在湍流成分，影响气流与覆冰导线表面的附着与分离，使得实际覆冰导线气动力特性与试验结果产生偏差。

利用CFD数值模拟技术是风洞试验之外研究覆冰导线气动力系数的另一种方法，黄河、吕翼等都曾采用非稳态算法获取覆冰导线的气动力时间历程，进而得到各攻角下时均化的气动力系数［11－12］，但与风洞试验比较表明CFD模拟结果仅能在一定程度上定性反映覆冰导线气动力系数随风攻角的变化趋势，具体数值则存在误差，且在气动力系数变化较快的攻角范围内误差显著。

由于覆冰状况的随机性与复杂性，目前已有成果还不能满足舞动研究的要求，累积各种冰型、冰厚以及风攻角下导线气动力系数仍是研究舞动及防舞所必须的工作之一。随着我国特(超)高压输电线路的建设，大截面输电导线得到了越来越广泛的应用，此类导线相比中低压及普通高压导线直径较大，以630/45和1000/45两型号为例，导线直径分别为33.6 mm和42.1 mm;而在2008年我国南方冰灾中，许多地区线路覆冰厚度超过了设计值，部分地区覆冰厚度达到40～60 mm。

本文制作了两种典型覆冰断面导线节段模型，在风洞中分别测量了其在均匀流和均匀湍流中的气动力特性，研究了风场中湍流对试验结果的影响。根据Den Hartog理论分别计算了两种断面覆冰导线可能发生舞动的风攻角范围，并结合以往试验结果，研究了两类覆冰冰型的气动力特征。

1 试验模型及设备

1.1 覆冰导线节段模型

输电导线的覆冰形状受覆冰时气象条件的影响:在低温微风且雨量较少的天气，水滴与导线表面一触即凝，将形成典型的新月形覆冰;若气温相对较高，且雨量较大，水滴在导线表面无法立即凝固，且由于风经过导线壁面流动产生分离点使得冰型外周产生角点，形成近似D形的覆冰截面形状。

试验所采用的两种典型覆冰断面形状如图1所示，导线及覆冰模型均采用有机玻璃制作，导线直径35 mm，D形覆冰断面为直径80 mm的半圆;新月形覆冰断面则为半圆与半椭圆的组合形状，其中椭圆短半轴长等于导线半径，长半轴长38.5 mm。节段有效长度为1 m。实际试验模型如图2所示。

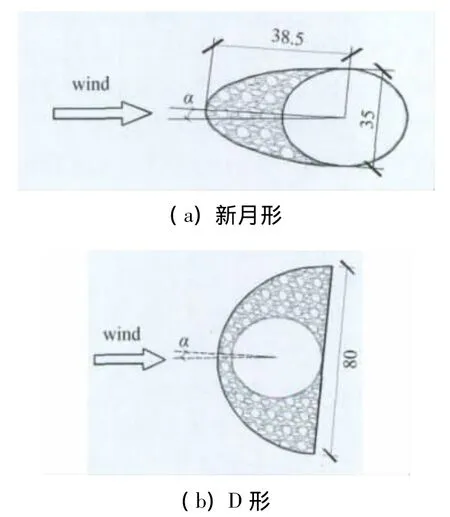
图1 试验覆冰导线断面形状及风攻角定义(单位:mm)Fig.1 Cross-section shape of iced conductors and definition of wind angle of attack(Unit:mm)

图2 风洞试验覆冰导线模型Fig.2 Model of iced conductors in wind tunnel

1.2 试验设备

本次试验在大连理工大学风洞试验室(DUT-1)进行，风洞试验段长18 m，横断面宽3 m，高2.5 m，空风洞最大设计风速50 m/s。根据实测资料，舞动发生风速通常小于20 m/s，多集中于7～15 m/s，同时为研究风场中湍流对导线气动力特性的影响，本文试验风速分为风速15 m/s均匀流场以及风速10 m/s的均匀湍流场。

覆冰导线舞动多发生在空旷地带，对应于我国荷载规范GB50009-2001的A类或B类地貌，由于我国规范对于风荷载湍流度缺乏明确规定，参考日本的荷载规范，湍流度随地面高度的变化采用以下理论公式描述:

式中Z是离地面高度，A是常数，当H=30m时，A=β。

假定导线所处高度离地面100m，对于A类地貌，β=0.12;B类地貌，β=0.16。此时导线高度的湍流度分别为10%和13%，限于风洞试验条件限制，难以实现较高的均匀湍流，故试验湍流度定为6% 。

通过在风洞试验段前端加装等距离横杆，如图3所示，使来流产生较为均匀的湍流。则试验雷诺数约为:

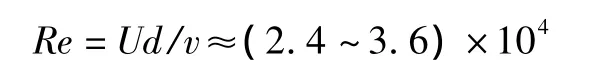
根据以往试验结果在试验雷诺数范围内风速变化对导线气动力系数的影响极小，故均匀流场与均匀湍流场风速的区别基本不影响试验结果，可认为两种流场下气动力特性的区别主要由湍流造成。

图3 风洞中均匀湍流实现方法Fig.3 Generation of isotropic turbulence in wind tunnel

试验测力设备为日本NITTA公司IFS-75E20A-1125EX高频测力天平，水平力测量量程为100 N，弯矩测量量程11N·m，测力频率8 kHz，精度0.61‰。试验时将测力天平置于风洞底部转盘中心，并将导线节段模型竖向放置于测力天平上，如图1所示定义风攻角，并顺时针转动转盘，转角步长为5°，考虑到模型的对称性，转角范围为 0°～180°。测量时天平采样频率200Hz，每个风攻角采样时间25s，采样点数为5000。由于模型长细比超过15，可近似认为满足二元流动，故模型顶部没有添加端板。试验模型及设备如图4所示。

图4 风洞试验模型及设备Fig.4 Wind tunnel test model and device

2 试验内容

风对覆冰导线断面的作用可表现为阻力FD，升力FL以及扭矩M，如图5所示，其相应的无量纲气动力系数如下所示:

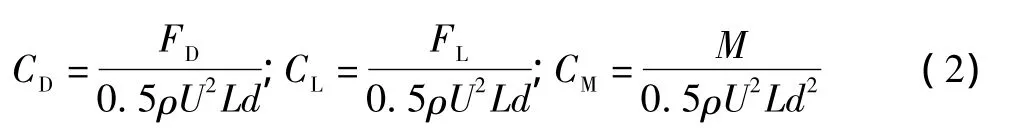
式中CD、CL、CM分别表示阻力系数、升力系数以及扭转系数，U为试验风速，ρ为试验时空气密度，L和d分别为试验导线节段的有效长度和有效迎风宽度，为使各风攻角下导线气动力系数便于比较，迎风宽度固定为导线直径。

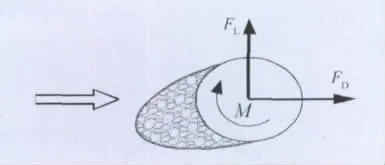
图5 气动三分力方向定义Fig.5 Definition of aerodynamic force components

试验所直接测得的水平力结果为天平X、Y轴力，由于天平坐标轴随风洞底盘转动，故需将各风攻角下天平轴力转化为风轴阻力和升力，并将高频采样得到的气动力时程进行时均化处理，最终通过式(2)转化为无量纲化气动力系数。

3 气动力特性试验结果

3.1 新月形覆冰导线

新月形覆冰导线各攻角下的气动三分力系数如图6～图8所示。升力系数曲线在中部由正变负呈波状变化，两侧在20°和165°附近各存在一向上尖峰，且尖峰位置所对应的阻力系数和扭矩系数曲线同样存在局部突变。阻力系数在0°～180°呈半波状分布，两端较小中间最大，反映了导线实际迎风宽度随攻角的变化;扭转系数同样两侧小中部大，除两端部分攻角为负外，其余范围均为正值，其最大值对应攻角为覆冰处于导线侧上方偏背风向位置。

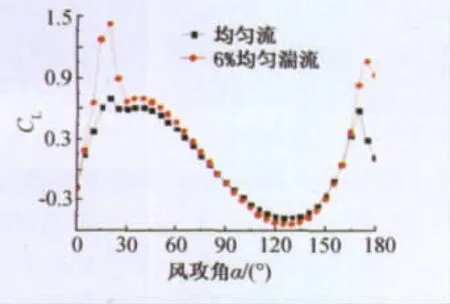
图6 新月形覆冰导线升力系数Fig.6 Lift coefficient of crescent section iced conductor

在试验雷诺数范围内，湍流对新月形覆冰导线气动力特性的影响则主要体现在两方面:首先在整体上略微提高了气动三分力系数的幅值，尤其由于湍流改变了气流经过覆冰表面的分离点位置，增大了气流与覆冰导线的接触范围，因而对阻力系数幅值的提高效果较为明显;其次，湍流加剧了覆冰表面气流的不对称性，显著提高了升力系数两侧尤其是左侧尖峰的峰值，同样也加大了对应攻角下阻力系数和扭矩系数的突变。结合后文分析可以看出，这对新月形覆冰导线舞动稳定性存在较大影响。

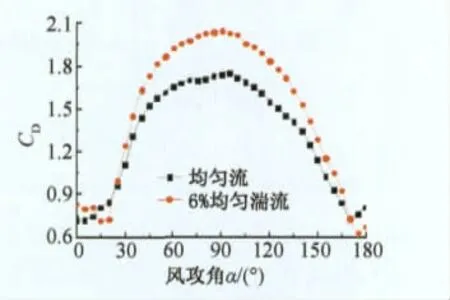
图7 新月形覆冰导线阻力系数Fig.7 Drag coefficient of crescent section iced conductor

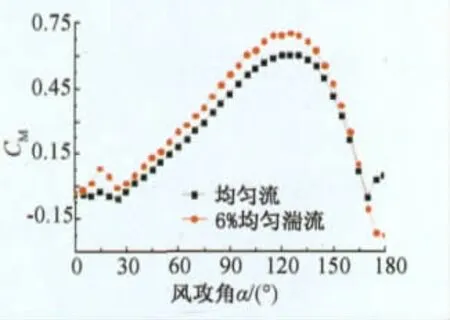
图8 新月形覆冰导线扭转系数Fig.8 Moment coefficient of crescent section iced conductor

3.2 D形覆冰导线

D形覆冰导线各攻角下的气动三分力系数如图9～图11所示。D形覆冰导线升力系数曲线呈现出两个相向尖峰，位于90°和135°攻角附近，后一尖峰即正向尖峰峰值较大，两尖峰外侧皆存在较大攻角范围的升力系数曲线负斜率区域。两峰值对应攻角下的阻力系数和扭转系数均存在局部突变。D形覆冰导线阻力系数曲线呈两端大中间小凹谷状分布，除实际迎风宽度变化的影响外，覆冰圆弧段迎风时，阻力系数相对较小，变化较为平缓;当直线段迎风时则阻力系数较大，变化速度快。扭转系数分布趋势与升力系数较为相似，覆冰圆弧段迎风时呈较为光滑的正向半波状分布，直线段迎风时则呈反向尖角分布，其正负峰值幅值接近。

另外可以发现，风场中湍流对D形覆冰导线升力系数影响相对较小，主要体现于降低前一尖峰左侧区域的负斜率，对后一尖峰仅略微提升了幅值;湍流对阻力系数两侧峰值提升较大，对扭转系数幅值0°至90°攻角范围的增大效果则较为显著。

3.3 Den Hartog舞动机理及其系数

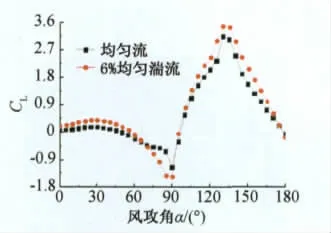
图9 D形覆冰导线升力系数Fig.9 Lift coefficient of D section iced conductor

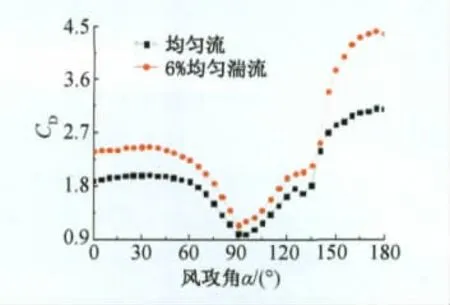
图10 D形覆冰导线阻力系数Fig.10 Drag coefficient of D section iced conductor

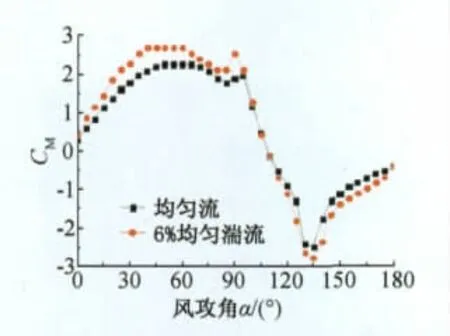
图11 D形覆冰导线扭转系数Fig.11 Moment coefficient of D section iced conductor

根据Den Hartog单自由度竖向舞动机理［1］，图12所示的覆冰导线截面模型，在风速U机理下，产生y向振动，振动速度为，攻角为α，其运动方程可表示为:

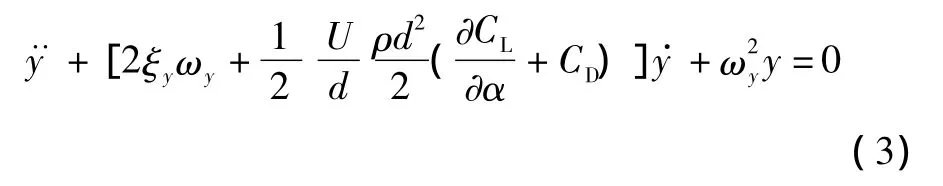
式中，ωy为系统竖向固有频率，ξy为系统竖向阻尼比。系统的稳定性取决于其阻尼项的正负，当系统阻尼项为负时将发生失稳。可见，当覆冰导线满足:

时，且风速超过临界风速Uc输电线路即将发生舞动，临界风速 Uc可表示为［13］:

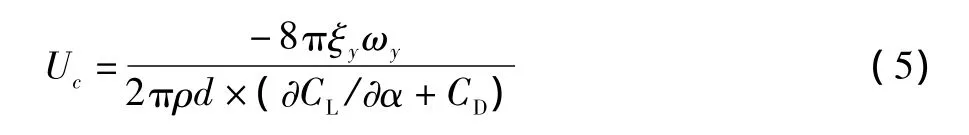
式(4)等式左端即为Den Hartog系数，可以发现，影响导线Den Hartog系数的气动参数主要为升力系数斜率和阻力系数，采用求试验值两点间斜率的方法计算升力系数对攻角的导数，可得两种覆冰断面的Den Hartog系数如图13、图14所示。

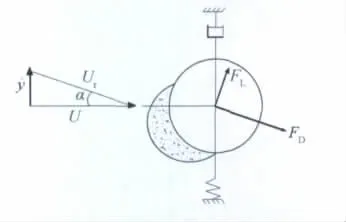
图12 覆冰导线Den Hartog舞动模型Fig.12 Model of iced conductor Den Hartog galloping

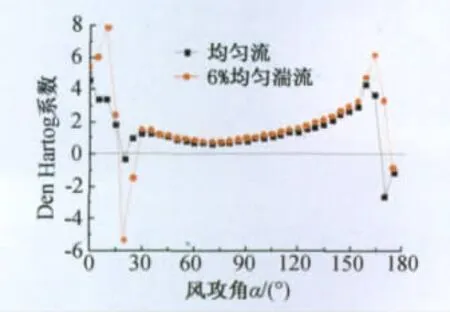
图13 新月形覆冰导线Den Hartog系数Fig.13 Den Hartog coefficient of crescent section iced conductor

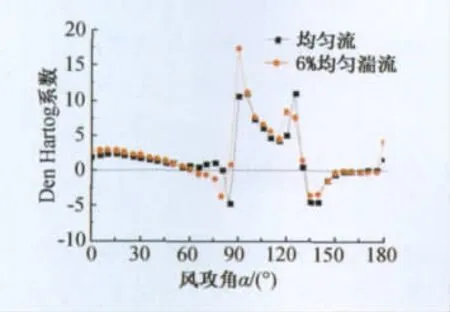
图14 D形覆冰导线Den Hartog系数Fig.14 Den Hartog coefficient of D section iced conductor

对新月形覆冰而言，其不稳定攻角范围存在于试验攻角范围两侧，即15°～30°和175°～180°范围内。导线形成新月形覆冰后，考虑覆冰静扭矩的影响，风攻角极易落入前侧不稳定范围内;若风向改变使其与线路正交分量反向，则风攻角仍然易处于后侧不稳定范围内，可见新月形覆冰导线的气动力特性在覆冰形成后初始条件下便易于诱发舞动。另外可见，风场中湍流加大了升力系数曲线两侧尖峰峰值，但却降低了后一尖峰下降段的负斜率，因而湍流仅增大了前一不稳定攻角范围，并降低了起舞临界风速，却减小了后一不稳定范围。

D形覆冰导线Den Hartog系数的负值则出现在65°～85°及135°～150°范围内，即升力系数两尖峰的外侧负斜率区域，相比新月形断面，其不稳定攻角范围较宽，因而D形覆冰导线在覆冰静扭矩及气动扭矩联合作用下落入不稳定攻角范围诱发舞动的概率同样很大。湍流对D形覆冰导线Den Hartog系数的影响主要在于增强了65°～85°攻角范围内即升力系数曲线前侧尖峰的负斜率，使该范围下Den Hartog系数由均匀流下的略大于0变为负值，增大了D形覆冰导线的舞动范围;而湍流对升力系数曲线后侧尖峰的影响使均匀流下不稳定的85°攻角反而成为稳定攻角。

4 以往试验结果

导线覆冰冰型、冰厚等均具有不确定性，针对某特定覆冰断面的单次风洞试验尚不足以掌握此类冰型的气动力特性，为此本文将本次试验均匀流场下所得结果结合以往试验结果进行比较，由于各试验所用导线直径、覆冰冰厚及冰型细节均有所差别，故此处仅能定性反映两类覆冰冰型气动力的总体特征及变化规律。以往试验导线及覆冰断面形状如图15所示，各试验所得升力及阻力气动力系数曲线如图16～图19所示。

试验(b)与本次试验新月形覆冰冰型差异较大，主要表现为覆冰厚度较小，形状较为圆滑;试验(a)和(c)与本次试验较为接近，因而其升力及阻力系数曲线与本试验结果变化规律较一致，升力系数曲线皆存在正负波状变化和两侧尖峰，阻力系数曲线则均为中间大两侧小;试验(b)断面升力系数曲线则波状变化趋势不明显，且不存在后侧尖峰，其阻力系数曲线表现为3个正向半波分布，外侧半波范围较小，中间半波范围较大，半波峰值较为接近。本次试验与以往试验3种D形覆冰冰型接近，因而在共同的试验攻角范围内分布规律较为一致，但由于以往试验攻角范围有限，故无法从全局反映D型覆冰导线气动力特性。

试验(b)与本次试验新月形覆冰冰型差异较大，主要表现为覆冰厚度较小，形状较为圆滑;试验(a)和(c)与本次试验较为接近，因而其升力及阻力系数曲线与本试验结果变化规律较一致，升力系数曲线皆存在正负波状变化和两侧尖峰，阻力系数曲线则均为中间大两侧小;试验(b)断面升力系数曲线则波状变化趋势不明显，且不存在后侧尖峰，其阻力系数曲线表现为3个正向半波分布，外侧半波范围较小，中间半波范围较大，半波峰值较为接近。本次试验与以往试验3种D形覆冰冰型接近，因而在共同的试验攻角范围内分布规律较为一致，但由于以往试验攻角范围有限，故无法从全局反映D型覆冰导线气动力特性。

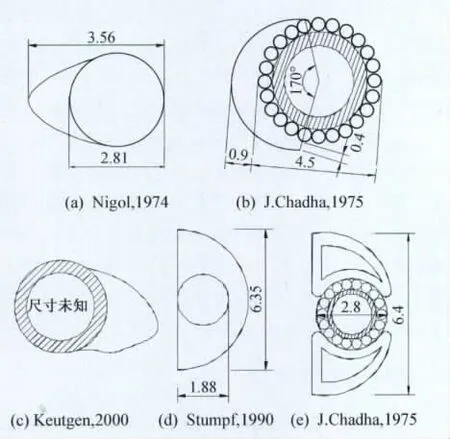
图15 以往试验中覆冰导线断面形状(单位:cm)Fig.15 Cross-section shape of iced conductors in earlier tests(unit:cm)

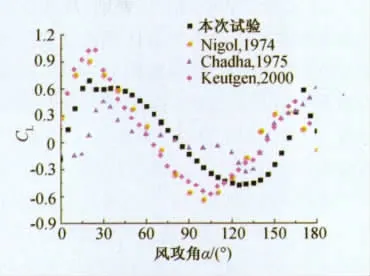
图16 各试验新月形覆冰断面升力系数Fig.16 Lift coefficient of all crescent section iced conductor

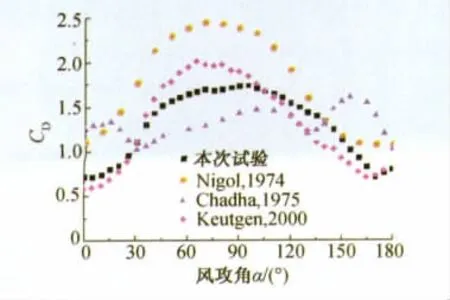
图17 各试验新月形覆冰断面阻力系数Fig.17 Drag coefficient of all crescent section iced conductor

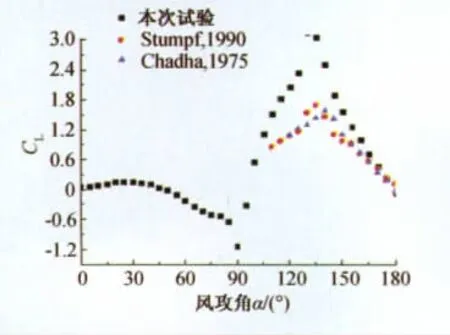
图18 各试验D形覆冰断面升力系数Fig.18 Lift coefficient of all D section iced conductor

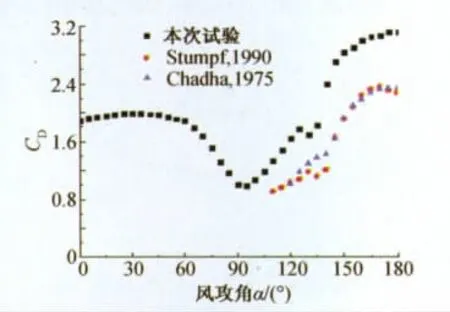
图19 各试验D形覆冰断面阻力系数Fig.19 Drag coefficient of all D section iced conductor

5 结论

本文通过在风洞进行覆冰导线节段模型的测力试验，获取了新月形及D形覆冰导线的气动三分力系数及其随风攻角的变化规律，研究了流场湍流对其影响，主要结论如下:

(1)新月形覆冰导线升力系数曲线呈正负波状变化，两侧攻角存在尖峰;阻力系数及扭转系数则均为中间攻角范围大两侧攻角范围小。湍流显著提高阻力系数幅值，并增强了升力系数两侧尖峰。

(2)D形覆冰导线阻力系数呈现两相向尖峰分布，后一正向尖峰峰值较大，阻力系数两侧大中间小，扭转系数则由一正向半波和一反向尖峰组成。湍流主要提高扭转系数0°至90°攻角范围和阻力系数幅值，对升力系数影响较小。

(3)新月形覆冰导线可能发生Den Hartog舞动的攻角范围为15°～30°和175°～180°，D 形覆冰导线则为65°～85°及135°～150°;均匀流与湍流环境下覆冰导线发生舞动的攻角范围及其起舞风速存在一定差异。

(4)结合以往试验结果表明，本试验结果能够反映各类厚覆冰新月形和D形覆冰导线气动力的共同特征，薄覆冰新月形导线气动力特性则与本试验存在较大差异。

［1］Den HARTOG J P.Transmission line vibration due to sleet［J］.AIEE，51，1932，part 4:1074-1086.

［2］NIGOL O，BUCHAN P G.Counductor gallioing 2:torsional mechanism［J］.IEEE Transactions on Power Apparatus and Systems，1981，100(2):708-720.

［3］YU P，SHAH A H，POPPLEWELL N.Inertially coupled galloping of iced conductors［J］.Journal of Applied Mechanics-Transactions of the ASME，1992，59(1):140-145.

［4］NIGOL O，CLARKE G J.Conductor galloping and control based on torsional mechanism［C］.IEEE Power Engineering Society Winter Meeting Paper，No.C74016-2，New York，1974.

［5］RENAUD K，JEAN-LOUIS L.Benchmark cases for galloping with results obtained from wind tunnel facilities-validation of a finite element model［J］.IEEE Transactions on Power Delivery，2000，15(1):367-374.

［6］STUMPF P，NG H C M.Investigation of aerodynamic stability for selected inclined cables and conductor cables［D］.［B.Sc.Thesis］.University of Manitoba，Winnipeg，Canada，1990.

［7］CHADHA J，JASTER W.Influence of turbulence on the galloping instability of iced conductors［J］.IEEE Transactions on Power Apparatus and Systems，1975，94(5):1489-1499.

［8］李万平，杨新祥，张立志.覆冰导线群的静气动力特性［J］.空气动力学学报，1995，13(4)，427-435.

［9］SHIMIZU M，et al.A wind tunnel study on quasi-steady and unsteady forces of ice accreted four bundled and single conductor transmission lines［J］.CRIEPI REP，U03044，2004.

［10］李万平，黄河，何锃.特大覆冰导线气动力特性测试［J］.华中科技大学学报，2001，29(8):84-86.

［11］黄河，刘建军，李万平.覆冰导线气动力特性的数值模拟［J］.工程力学，2003，(增刊):201-204.

［12］吕翼.覆冰导线气动力特性的数值模拟研究［D］.浙江大学，2008.

［13］郭应龙，李国兴，尤传永.输电线路舞动［M］.中国电力出版社，2003.