微小型螺旋桨滑流内舵面操纵特性实验研究
吴大卫,王 亮,李寒冰,李 书
(北京航空航天大学航空科学与工程学院,北京 100191)
0 引言
近几年的局部战争和自然灾害中无人机的重大作用逐渐体现,而微小型垂直起降飞行器因其特有的任务剖面和飞行性能,其发展更是方兴未艾。除传统的直升机外,此类飞行器具有涵道风扇式[1],倾转旋翼/机翼式[2],坐地起降式[3-4]等各类总体方案。由于重量和系统复杂性的限制,上述方案很多放弃了总距和周期变距操纵机构,而采用固定桨距螺旋桨提供垂直升力和前飞推力,悬停时的姿态控制通过螺旋桨滑流中的舵面偏转来实现。
此类飞行器在悬停时稳定性和抗风能力较差,在保证起飞重量的同时需要操纵系统能够提供较大的操纵力矩储备以保证垂直起降过程中的飞行安全和机动性;但在试飞过程中却往往发现滑流舵操纵效率不足的问题。关于螺旋桨对翼面的气动干扰,国内外曾进行了一定的理论和实验探索[5-7]。由于翼面处于较高湍流度的非定常螺旋桨滑流中,使用常规的翼型数据进行估算往往误差较大,采用CFD计算也对湍流模型的选择和设置有较大难度且计算效率较低。实验方面,由于各类研究对象独有的复杂性,尤其对于垂直起降飞行器悬停状态时,气动力的无量纲化难以衡量不同设计方案的优劣,这些结果都很难在更广的设计领域普适。这造成此类飞行器滑流舵的操纵特性还缺乏针对各种设计参数和构型的系统性实验研究。综上,目前对此类设计问题还缺乏足够的理论指导和实验数据支持,使此类飞行器的总体设计和飞行力学建模较为困难。
本文选用了不同型号的微小型螺旋桨,对静推力状态时螺旋桨滑流内舵面的操纵特性进行了系统性的实验研究,并最终给出了螺旋桨的不同几何参数、桨盘平面位置、舵面中央切口、翼梢端板、正交翼面等因素对操纵特性影响的一系列结论,并给出了物理解释,为提高此类微小型垂直起降飞行器的操纵效率提供了实验依据。由于螺旋桨处于悬停时静推力状态,为了方便不同状态的数据分析对比,本文对实验数据不进行无量纲化,这是与固定翼飞机前飞状态气动特性研究具有明显区别的。
1 实验设备
1.1 实验用螺旋桨
实验用螺旋桨采用向厂家定制的木质几何定距螺旋桨,剖面翼型基本为12%相对厚度的ClarkY平凸翼型,桨根相对厚度逐渐过渡为15%以上。其主要参数为直径D,几何螺距H和A、B两种平面形状,桨叶实度约0.07,片数均为2。其中几何螺距H按0.7倍半径R处翼型下弧面直线段的桨叶角β0.7确定,并在有效工作段维持定值:

桨叶典型平面形状、弦长c分布和桨叶角β分布见图1。实线为 H/D=0.3、0.5、0.7 三种条件下 β 随 r/R的变化,虚线为A、B两种桨型的c/D随r/R的变化。本文的实验用桨D=(220~360)mm,输入功率P<350W,桨尖马赫数 Matip<0.5Ma,叶素雷诺数Re<300000。
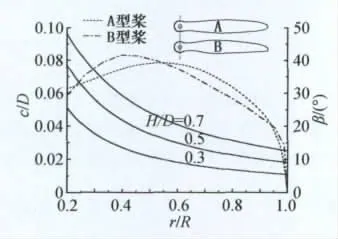
图1 实验用螺旋桨的典型几何特征Fig.1 Geometric characters of typical tested propellers
1.2 操纵力矩测量设备
由于在小型应变天平上安装螺旋桨易造成“地面共振”严重影响实验精度,本文自行设计实验装置见图2:由回转支架、CFBH型静扭矩传感器(量程10N·m,精度0.03%)、光敏电阻式转速计、无刷直流电机(额定功率700W,最大效率78%)与螺旋桨、XST/A可编程数字式仪表以及方向舵偏角可调的尾翼等组成。该系统可通过仪表直接读数也保留了计算机通讯接口,测得的偏航操纵力矩数据须通过密度比换算到标况大气下。图2中尾翼采用 NACA0012翼型,弦长0.2m,展长0.4m,简单式舵面宽度为0.06m。尾翼1/4弦线到扭矩传感器扭力轴的力臂长度为0.95m。为减小螺旋桨引起的振动对偏航操纵力矩读数的影响,在台架尾端可增设阻尼器。该系统成本较低,气动干扰小,实验表明具有良好的数据重复性。

图2 操纵力矩测量系统Fig.2 System for measuring control moment
1.3 螺旋桨性能标定装置
不同型号螺旋桨静推力T、功率P随转速变化特性可分别通过如图3所示的两套试车台进行标定。系统采用的支架和数据采集仪器与上述操纵力矩测量装置基本通用,通过对支架、传感器以及动力装置进行简单改装便可实现不同功能的转化。通过空气密度比换算,所得标况下典型螺旋桨原始实验数据如图4。性能曲线采用四次以内多项式最小二乘拟合可以具有很好的结果。

2 实验结果分析
2.1 操纵力矩与舵偏角的关系
图5给出了不同转速下偏航力矩与舵偏角δr的关系。可认为在选定螺旋桨的某一转速下,30°正常偏角内,偏航力矩与舵偏角呈现较好的线性关系。这有助于建立此类飞行器悬停时的线性动力学模型。更大的舵偏角将导致螺旋桨滑流的严重分离,破坏线性关系。值得注意的是,随着转速的提高,滑流动压的增强,滑流舵工作的线性范围也获得一定的扩展。
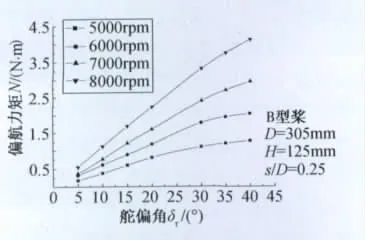
图5 偏航力矩与舵偏角的关系Fig.5 Yaw moment versus angle of rudder deflection
2.2 桨盘位置对操纵力矩的影响
文献[8]给出螺旋桨诱导速度因子kd与桨盘平面距离s的关系:

上式表明悬停时桨盘远后方轴向诱导速度将变为桨盘处的2倍,而滑流区域的直径将收缩为约0.707D。一般认为操纵力矩N正比于滑流区内翼面积Sslip和滑流动压qslip:

式(2、3)表明s值越大,舵效则越强。而文献[9]指出桨盘后0.25R处螺旋桨滑流就几乎完成了收缩过程。图6给出了桨盘平面与尾翼前缘的距离s对偏航力矩的影响。
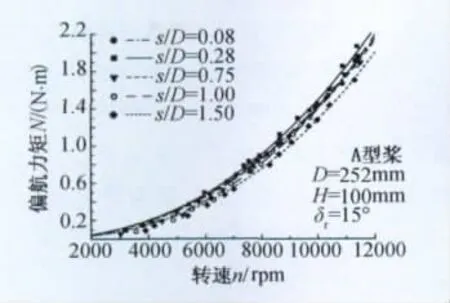
图6 桨盘前后位置对偏航力矩的影响Fig.6 Effect of propeller disk position on yaw moment
图6表明在s/D<1的范围内操纵力矩基本不受桨盘位置影响。当s/D<0.1时由于尾翼前缘过分接近桨盘平面,阻滞作用增强,滑流动压下降,因此舵效也略微下降。当s/D达到1.5以上时,由于桨盘平面较远,滑流强度衰减造成舵效较快的下降。实验也证实了螺旋桨滑流收缩迅速,可以认为此类飞行器悬停时螺旋桨滑流在翼面处已经完成收缩。本文推荐s/D取0.2~0.5可保证获得最强的舵效,结构设计上也是易于实现的。
2.3 螺旋桨几何参数对操纵力矩的影响
文献[10]把螺旋桨滑流内的气动舵面等同于喷气发动机作用的燃气导流板,认为舵面偏转实质上是改变了滑流方向,产生了“推力矢量效应”,因此一定静推力下的舵效只与舵面的偏转角度有关。
本文假设滑流尾迹在尾翼前缘处充分收缩,根据动量法[9]偏航力矩为:
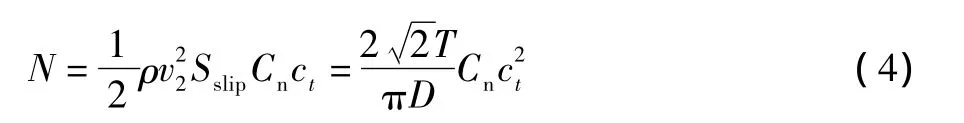
ct为尾翼弦长,v2为充分收缩后的轴向诱导速度,Cn为某一舵偏角下偏航力矩系数。从(4)式可以看出操纵力矩正比于T/D,即在总重相同(静推力亦相同)的情况下悬停,螺旋桨直径越小舵效越强,这对文献[10]的结论是重要补充:对于图7方向舵偏角为15°的情况,若忽略零升力矩,认为偏航力矩都是由侧力产生,则对于最小直径的螺旋桨,滑流产生了约8.2°的当量偏转,而对于最大直径的螺旋桨这一数值仅约为6.1°。上述结果主要由于小直径螺旋桨很高的滑流动压远远胜过了滑流区域较小的不利因素,此外由于小直径螺旋桨滑流区域更集中于舵面附近,能有效地改变整个尾迹的方向,更接近“推力矢量效应”。图7选取不同直径的几支A型桨绘制出偏航力矩随静推力的变化曲线,线性程度很好且证实了上述正比例关系的正确性。

图7 螺旋桨直径不同时的偏航力矩随静推力变化曲线Fig.7 Yaw moment versus static thrust with different propeller diameters
当舵面偏角 δr=15°,静推力 T=15N,选取 D=305mm但几何螺距和平面形状都不同的几支螺旋桨,实验结果如表1。结果进一步表明(4)式的合理性:几何螺距虽然会影响螺旋桨给定静推力下的需用功率,但对舵面操纵力矩几乎没有影响;而由于B型桨的最大弦长接近根部,轴向诱导速度也在根部分布较为集中,因此舵面偏转造成的“推力矢量效应”更加明显,舵效略高。
总之,直径相等的各种型号螺旋桨对应某一静推力下的滑流舵操纵效能基本是等效的,其他几何参数可以按照减小悬停需用功率,提高巡航推进效率的原则来选取。
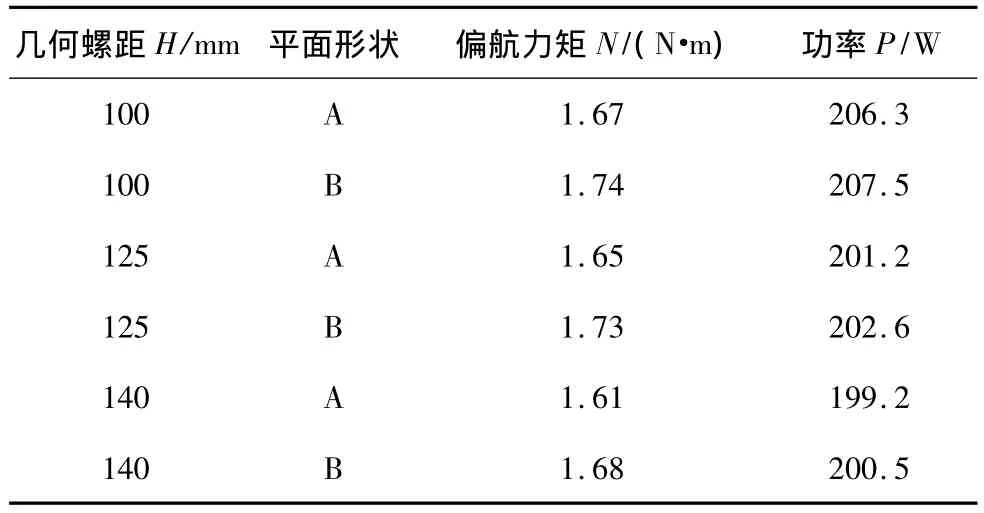
表1 若干相同直径的螺旋桨实验数据对比Table 1 Testing data of some propellers with the same diameter
最后指出虽然减小螺旋桨直径有利于改善操纵特性,但是通过标定螺旋桨的功率证实过高的桨盘载荷将导致悬停需用功率显著增加,因此需要折衷考虑。
2.4 翼梢端板的影响
本文用于实验的垂直尾翼展弦比为2,升力线斜率相对其翼型下降很多。在不少资料提供的设计方案中为减小翼梢损失对滑流中舵效的不利影响,增加了翼梢端板,旨在增加翼面的有效展弦比,但并未有资料定量的给出对操纵效率的改善效果。本文对原垂直尾翼两端都安装了大面积的端板,进行了定量实验,端板的某一几何形状和典型实验数据如图8、图9所示。

图8 端板安装状态Fig.8 Test condition with endplate
图9给出了有无端板两种状态,分别选取直径一大一小两支螺旋桨得出的滑流舵偏转时的偏航力矩原始数据。可以看出安装端板后的数据点分布都略微上升但总体上端板改善舵效的能力是比较微弱的,这一点与对翼梢端板功效的传统认识有较大区别。图9还给出了同等静推力下,安装端板与未安装时的偏航力矩比值η随D/bv的关系(bv为尾翼展长):随着螺旋桨直径的增加,螺旋桨滑流的翼梢效应开始显现,端板改善操纵特性的效果缓慢上升,可以预见当螺旋桨直径增加到与翼展相等时舵效增加约10%。因此可以推测类似中小展弦比机翼在直匀流中的翼梢损失特性不会对螺旋桨滑流舵的操纵力矩产生显著影响,这可能归因于螺旋桨的诱导速度分布在桨尖较小。图9选取的螺旋桨为A型桨,实验表明对于最大弦长接近桨根的B型桨,诱导速度集中分布区域更远离桨尖,因此端板的改善效果也更微弱。此外,螺旋桨滑流区截面为圆形,受翼梢效应影响较显著的外侧区域流量较小也可能是导致上述实验结果的一个原因。实验中曾选用不同的端板后掠角、根梢比以及滑流舵偏角,得到的结论是相同的。
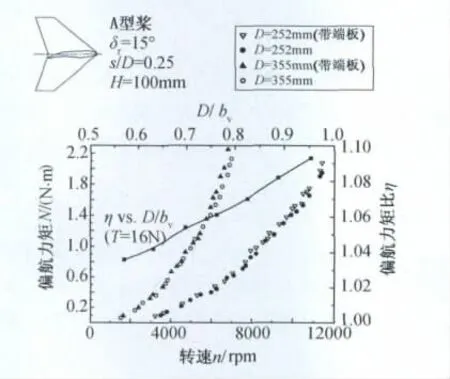
图9 不同螺旋桨直径时端板对偏航力矩的影响Fig.9 Effect of endplate on yaw moment with different propeller diameter
综上,若设计方案中采用大直径,平面形状类似A型的螺旋桨,采用翼梢端板能够对滑流舵操纵效能有所提升,反之则提升效果微弱。
2.5 舵面中央切口的影响
在很多微小型垂直起降飞行器设计方案中螺旋桨滑流中往往布置了十字形正交的翼面[3-4],可进行两个轴的姿态操纵。若正交翼面上的舵面偏转时出现干涉,必须其中一块设计成中央切口的双段舵。本文针对这种构型对原尾翼进行了修改,螺旋桨轴线处即舵面中央切口角度为60°,外形和典型实验数据如图10、图11。
假设滑流尾迹完全收缩,则对于图10中直径分别为254mm和355mm的螺旋桨,中央切口分别减小了滑流区内舵面面积的21%和15%,若滑流为直匀流,则三维效应造成的舵效损失更应当超过此数值。图10还给出了舵面带中央切口时与完整舵面的偏航操纵力矩比值η。可以看出在静推力T较大时,舵效损失远未有预测的高。这可能归因于螺旋桨轴向诱导速度在桨根处的分布很小,因此中央切口造成的“泄压”作用也就不明显。同样的原因,图11表现出最大弦长远离桨根的A型桨的舵效损失对舵面中央切口的存在更不敏感,其舵效损失比相同直径的B型桨低约30%。
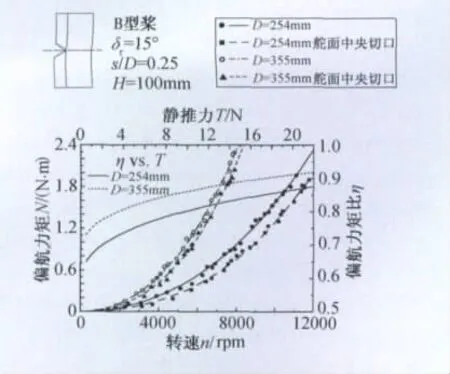
图10 不同螺旋桨直径时中央切口对偏航力矩的影响Fig.10 Effect of central gap on yaw moment with different propeller diameter
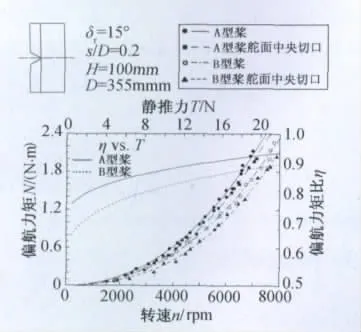
图11 不同螺旋桨平面形状时中央切口对偏航力矩的影响Fig.11 Effect of central gap on yaw moment with different propeller planforms
综上,对于上述舵面构型,推荐采用大直径,平面形状类似A型的螺旋桨,可以将中央切角的不利影响降到最低。
2.4和2.5节的实验结果都说明,螺旋桨滑流流过舵面偏转的三维翼面时与流过二维翼型的效果十分近似,尤其在较大静推力状态时。
2.6 “十”字形正交翼面的影响
文献[5]通过实验研究了涵道螺旋桨滑流内正交的全动舵面的气动干扰问题:由于没有安定面,全动舵面的大角度偏转将造成自身的深度失速,同时并列的多片舵面还会造成很强的“阻塞效应”,降低滑流动压,造成与之正交的舵面的气动效率明显下降。本文采用的“十”字形尾翼具有较大弦长的安定面,平尾的几何尺寸和前后安装位置与上文垂尾相同,方向舵为完整舵面,升降舵为避免干涉采用了60°的中央切口。图12给出了采用不同直径螺旋桨,升降舵和方向舵偏角都为30°时的偏航操纵力矩数据点,同时也给出单独垂尾时的实验结果作为对比。
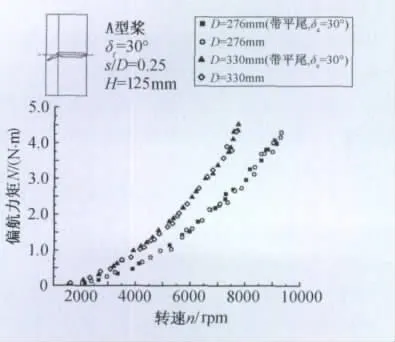
图12 有无平尾时的偏航力矩实验数据对比Fig.12 Yaw moment data with or without horizontal tail
图12中不同实验状态数据点的接近程度表明正交的“十”字形翼面间气动干扰微弱,即使在舵面偏角都较大的情况下依然可以视作每片滑流舵的独立工作。可推断因为此种构型对螺旋桨造成的“阻塞效应”很小,螺旋桨的轴向诱导速度并未受到显著影响。因此,前几节的实验结果可直接用于具有正交翼面的场合,这对垂直起降飞行器不同体轴间操纵解耦具有积极意义。
3 结论
本文通过选取不同几何构型翼面和不同型号微小型螺旋桨,测量螺旋桨静推力状态下舵面的偏航操纵力矩得到的结论如下:
1)滑流舵操纵力矩在正常舵偏角范围内基本呈线性关系,滑流动压越大线性范围也越宽;
2)螺旋桨静推力状态尾迹收缩迅速,桨盘到翼面前缘距离s对舵效影响不大,推荐s/D取0.2~0.5;
3)静推力T恒定时选取的螺旋桨直径D越小滑流舵操纵力矩越大,且近似正比于T/D,与螺旋桨其他几何参数关系不大;
4)翼梢端板能增加翼面的有效展弦比。当选用大直径,梢部宽弦特征的螺旋桨时,翼梢端板对滑流舵操纵效率有所增强,反之则增强效果微弱;
5)当舵面中央切角位于螺旋桨轴线处,在螺旋桨较大静推力时,舵效下降远小于舵面积的损失比例,推荐此时使用大直径,梢部宽弦特征的螺旋桨;
6)可认为螺旋桨滑流动压较大时,受翼面三维效应影响较小;
7)具有较大弦长安定面时,舵面偏转造成的“阻塞效应”较小,且“十字形”正交翼面之间的气动干扰很弱,可分别独立考察。
基于本文的实验数据和结论,今后将发展合适的理论计算方法研究此类问题,用于有关微小型垂直起降飞行器的飞行力学建模。本文的实验数据亦可直接用于起飞重量2~8kg的此类微小型垂直起降飞行器的悬停操纵导数估算。
[1]CHOI S W,KIM Y S,LEE J S.Design and test of small scale ducted-prop aerial vehicle[R].AIAA 2009-1439.
[2]MURAOKA K,OKADA N,KUBO D.Quad tilt wing VTOL UAV aerodynamic characteristics and prototype flight test[R].AIAA 2009-1834.
[3]KUBO D,MURAOKA K,OKADA N.Flight testing of a wing-in-propeller-slipstream mini unmanned aerial vehicle[R].AIAA 2009-2070.
[4]STONE R H,ANDERSON P,HUTCHISON C,et al.Flight testing of the T-wing tail-sitter unmanned air vehicle[J].Journal of Aircraft,2008,45(2):673-685.
[5]张德先,陈仁良.高速直升机涵道风扇矢量推进系统模型悬停状态的气动力测量研究[J].空气动力学学报,2009,27(3):281-287.(ZHANG D X,CHEN R L.Measurement investigation on the aerodynamics of vectored thrust ducted propeller[J].ACTA Aerodynamic Sinica,2009,27(3):281-287.)
[6]HUNSAKER D,SNYDER D.A lifting-line approach to estimating propeller wing interactions[R].AIAA 2006-3466.
[7]MCVEIGH M A,GRAY L,KISIELOWSKI E.Prediction of span loading of straight-wing-propeller combinations up to stall[R].NASA CR-2602,1975.
[8]STONE R H.Aerodynamic modeling of the wing-propeller interaction for a tail-sitter unmanned air vehicle[J].Journal of Aircraft,2008,45(1):198-210.
[9]普劳蒂.直升机性能及稳定性和操纵性[M].北京:航空工业出版社,1990.(PROUTY R W.Helicopter performance,stability,and control[M].Beijing:Press of Aviation Industry,1990.)
[10]MCORMICK B W.Aerodynamics of V/STOL flight[M].New York:Academic Press,1969.

