基于CFD技术的脊状表面湍流流场特性研究
刘占一,宋保维,黄桥高,胡海豹
(西北工业大学航海学院,陕西西安 710072)
0 引言
源自于鲨鱼皮的脊状表面减阻技术已被人们成功应用于石油输运、航空、航海、泳衣制造等广大的领域。人们对脊状表面的研究逐渐深入,在通过改变脊状结构形状尺寸以追求减阻效果最大化的同时,对脊状表面减阻机理的研究也从来没有停止过。
美国航空航天局兰利研究中心的Walsh是最早开始系统研究脊状表面的学者之一,他通过大量的风洞试验得出结论:在脊状结构无量纲尺寸小于30时,脊状表面存在减阻效果;脊状结构附近形成的“二次涡”与流向涡的相互作用是脊状表面减阻的重要原因[1-2]。日本的Yuji Suzuki利用三维粒子测速设备在水洞进行了脊状表面减阻试验,发现脊状结构能抑制顺流向的能量向法向和展向转化,从而实现减阻[3],而El-Samni也通过对矩形管道进行的数值模拟研究得到了类似的结论[4]。Haecheon Choi等利用直接数值模拟方法发现:脊状结构无量纲尺寸小于20时,由于流向涡尺寸大约在30左右,无法深入脊状结构,只能停留于脊状结构顶部,因此脊状结构内(除顶部区域)流动较为安静,壁面剪应力相比光滑表面减小了[5]。本文对一系列表面布置不同尺寸顺流向脊状结构的表面利用CFD方法进行了湍流状态下的数值模拟,并对脊状表面湍流流场特性进行了分析。
1 基于CFD技术的计算方法
本文选取的是一段三维的计算域,如图1所示。

图1 计算域Fig.1 Computation region
计算域底面沿x方向分为两段,前段为平板,作为发展段,后段为测试段,用来对比研究脊状表面和光滑表面。脊状结构沿流向布置,截面形状均为高宽相等的V型。计算选取的脊状结构无量纲尺寸s+从6.7至43.7 不等。
s+的定义为:,其中s为脊状结构实际尺寸,u*为壁面摩擦速度,v为流体介质的运动粘性系数。

图2 脊状结构附近网格(垂直流向的截面图)Fig.2 Grids near riblet structure(section perpendicular to flow direction)
脊状结构附近网格如图2所示,脊状结构内采用三棱柱网格,其他区域采用六面体网格。此次计算模拟的是平板表面脊状结构的流场特性,因此计算域上表面设置为对称边界条件。为避免侧壁干扰,计算域两个侧面也都设置为对称边界。入口面设置为速度入口,为了保证测试段处于湍流状态,笔者编制程序在入口面设定了一个已充分发展为湍流的速度分布。出口面为自由流。
本文所用流体介质为水,控制方程为雷诺平均N-S方程。计算选取的湍流模型为Reynolds应力方程模型(Reynolds Stress equation Model,简称 RSM),意在着重分析脊状结构对近壁区雷诺应力分布造成的影响。该湍流模型更加严格地考虑了流线型弯曲、旋涡、旋转和张力的快速变化,对于复杂流动有更高的精度预测潜力。
流场数值计算采用SIMPLE方法,SIMPLE算法是目前工程上应用最广泛的一种流场计算方法,主要用于求解不可压流场。其核心是采用“猜测—修正”的过程,在交错网格的基础上来计算流场,从而达到求解动量方程的目的[6]。文献[7]曾利用SIMPLE方法对三维湍流流场进行数值分析,获得了与试验相吻合的湍流特性[7]。
作者也曾利用该方法对具有不同间隔的脊状表面进行了湍流减阻研究,发表于《系统仿真学报》2009年19 期[8]。
2 结果及分析
2.1 与实验值的比较
图3给出了脊状表面减阻效果随脊状结构无量纲尺寸s+的变化规律,并与 Walsh试验所得结果[1]进行了比较。Walsh所采用的脊状结构截面形状同样是宽高相等的V型。其试验在一个矩形截面的小型风洞进行,主流风速为 7.6m/s,雷诺数为 9.26 ×104,测得最大减阻量为8%。本文的计算中,雷诺数为9.95×105,所得最大减阻量为8.63%,此时s+=18.2,减阻量随s+变化规律与Walsh所测结果也基本一致,只是减阻量最大值对应的s+略有差别。

图3 脊状表面减阻效果与无量纲尺寸的关系Fig.3 Relation between drag reduction effect and non-dimension size
2.2 脊状结构附近流场
图4和图5分别给出了减阻和增阻情况下y-z面脊状结构附近速度矢量图。两种情况均可以观察到以下现象:在脊状结构顶部形成了一对反向旋转的流向涡对;这些涡将动量从脊状结构底部沿脊状结构壁面输运至顶部;涡在z方向的尺度决定于脊状结构的宽度,约为脊状结构宽度的一半。减阻和增阻情况下y-z面脊状结构附近流向涡对中速度最大值分别为外流场速度的 1.4%和 2.1%。

图4 y-z面脊状结构附近流线图(s+=18.2)Fig.4 Stream line around riblet structure in y-z plane(s+=18.2)

图6和图7分别给出了减阻和增阻情况下脊状结构附近流向涡涡量云图。将流向涡涡量利用公式无量纲化,则在减阻和增阻情况脊状结构附近流向涡中心处的该值分别为0.26和0.36,表明增阻情况(s+=39.4)下脊状结构附近流向涡强度比减阻情况(s+=18.2)下大。

图6 脊状结构附近流向涡涡量云图(s+=18.2)Fig.6 Contour of streamwise vorticity near riblet structure(s+=18.2)

图7 脊状结构附近流向涡涡量云图(s+=39.4)Fig.7 Contour of streamwise vorticity near riblet structure(s+=39.4)
2.3 雷诺正应力分布曲线
图8和图9分别给出了减阻和增阻情况下边界层近壁区x向雷诺正应力沿y方向分布曲线。由图可见,两种情况下脊状表面近壁区x向雷诺正应力较光滑表面均有明显下降。Walsh、Choi等在试验中也观察到了这一现象。但减阻情况下(s+=18.2)下降幅度更大,其峰值较光滑表面下降了16%,峰值位置与光滑表面基本一致。增阻情况(s+=39.4)下,相比光滑表面,峰值位置有所右移。两种情况下x向雷诺应力峰值大小、位置的差异反映出近壁区涡结构大小、强度的不同。

图8 x向雷诺正应力分布(s+=18.2)Fig.8 Normal stress distribution in x direction(s+=18.2)

图9 x向雷诺正应力分布(s+=39.4)Fig.9 Normal stress distribution in x direction(s+=39.4)
图10和图11分别给出了减阻和增阻情况下边界层近壁区y向雷诺正应力沿y方向分布曲线。减阻情况(s+=18.2)下,测量位置在脊状结构顶部时,y向雷诺正应力相比光滑表面在0<y+<70的区域明显下降;测量位置在脊状结构底部时,在0<y+<10时,y向雷诺正应力高于光滑表面,这是由脊状结构附近形成的流向涡引起的,而10<y+<70时,曲线与测量位置在顶部的曲线重合。而增阻情况(s+=39.4)下y向雷诺正应力相比光滑表面明显增大。
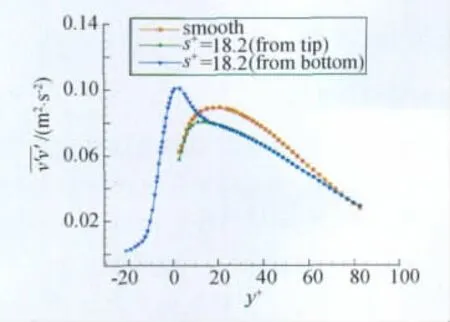
图10 y向雷诺正应力分布(s+=18.2)Fig.10 Normal stress distribution in y direction(s+=18.2)

图11 y向雷诺正应力分布(s+=39.4)Fig.11 Normal stress distribution in y direction(s+=39.4)
图12和图13分别给出了减阻和增阻情况下边界层近壁区z向雷诺正应力沿y方向分布曲线。两种情况下z向雷诺正应力相比光滑表面均明显下降,峰值大小和位置没有明显差别。脊状表面z向雷诺应力的减小表明脊状结构的存在确实对原本紊乱的近壁区流动有了横向限制,使流动的横向脉动降低。但是减阻情况下向雷诺正应力减小的区域为0<y+<70,增阻情况下这一区域为0<y+<50,原因在于增阻情况(s+=39.4)下,脊状结构内流向涡规模、强度均比减阻情况(s+=18.2)下大。

图12 z向雷诺正应力分布(s+=18.2)Fig.12 Normal stress distribution in z direction(s+=18.2)

图13 z向雷诺正应力分布(s+=39.4)Fig.13 Normal stress distribution in z direction(s+=39.4)
2.4 雷诺剪应力分布曲线
图14和图15分别给出了减阻和增阻情况下边界层近壁区雷诺剪应力沿y方向分布曲线。可以明显看出,减阻情况下,脊状表面雷诺剪应力较光滑表面在0<y+<70区域显著下降;增阻情况下,测量位置在顶部时,脊状表面雷诺剪应力较光滑表面明显变大,测量位置在底部时则在y+>40的区域明显变大。
2.5 壁面剪应力分布云图

图14 雷诺剪应力分布(s+=18.2)Fig.14 Shear stress distribution(s+=18.2)
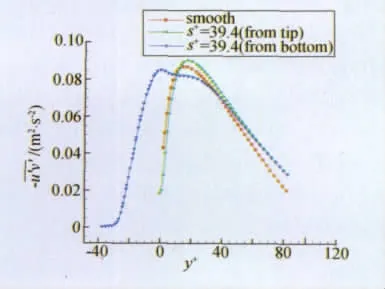
图15 雷诺剪应力分布(s+=39.4)Fig.15 Shear stress distribution(s+=39.4)

图16 脊状结构壁面剪应力分布云图(s+=18.2)Fig.16 Contour of wall shear stress distribution(s+=18.2)

图17 脊状结构壁面剪应力分布云图(s+=39.4)Fig.17 Contour of wall shear stress distribution(s+=39.4)
图16和图17分别给出了减阻和增阻情况下脊状结构壁面剪应力分布云图。由图可见,两种情况下脊状结构底部区域(深蓝色)剪应力都较小,剪应力较大的部分都集中在顶部区域(红色),这表明脊状结构底部流动较为安静,而顶部流动则十分剧烈,存在很强的动量交换,这从图4和图5所示的脊状结构附近流线图也可以看出。
3 脊状表面湍流流场特性分析
众多学者的理论及试验研究表明,湍流流动中近壁面的流向涡对于壁面剪应力有着决定性的影响。这些流向涡会导致强烈的下扫运动,使流动在壁面法向和展向方向产生动量交换,削弱了沿流动方向的能量。
本文的数值模拟结果反映出,在脊状结构附近产生了相对规则的流向涡,一个脊状结构内存在一对尺寸相当、反向旋转的流向涡对,单个流向涡尺寸大约是脊状结构尺寸的一半。笔者认为这些流向涡是脊状表面减阻或者增阻的重要原因,并从边界层近壁面各方向雷诺应力分布以及壁面剪应力分布等方面对脊状表面流场特性进行了分析。
图10和图12反映出脊状结构的存在限制了流向涡的尺寸以及流动的横向脉动,减小了壁面法向及展向的动量交换,流动方向能量转化为法向及展向能量的比例减少,从而产生了减阻效果。从本文得出的减阻效果随脊状结构无量纲尺寸变化图中可以看出,脊状结构的无量纲尺寸超过30之后,脊状表面表现出增阻。通过对增阻情况下脊状表面各个参数的分析发现,脊状结构无量纲尺寸超过30时,流向涡的尺寸及涡量明显增加,加上沾湿面积的增大,是可能出现减阻效果减弱甚至增阻现象的。
[1]WALSH M J.Riblets as a viscous drag reduction technique[J].AIAA Journal,1983,21(4)∶485-486.
[2]WALSH M J.Turbulent boundary layer drag reduction using riblets[R].Orlando:AIAA 20th Aerospace Sciences Meeting,1982.
[3]SUZUKI Y,KASAGI N.Turbulent drag reduction mechanism above a riblet surface[J].AIAA Journal,1994,32(1)∶1781-1790.
[4]El-SSMNI O A,CHUN H H,YOON H S.Drag reduction of turbulent flow over thin rectangular riblets[J].International Journal of Engineering Science.2007,45∶436-454.
[5]CHOI H,MOIN P,KIM J.Direct numerical simulation of turbulent flow over riblets[J].Journal of Fluid Mechanics,1993,255∶503-539.
[6]王福军.计算流体动力学分析[M].北京:清华大学出版社,2004.
[7]刘喜宁.基于SIMPLE方法下的三维湍流流场数值分析[D].[硕士学位论文].西北工业大学,2005.
[8]刘占一,胡海豹,宋保维.不同间隔脊状表面减阻数值仿真研究[J].系统仿真学报,2009,21(19)∶6025-6028.
[9]潘家正.湍流减阻新概念的实验探索[J].空气动力学学报,1996,14(3)∶304-310.
[10]李新华,董守平,赵志勇.减阻沟槽表面近壁湍流相干运动的实验研究[J].山东大学学报,2006,41(2)∶106-110,143.

