柔性机构时变可靠性分析的时变随机响应面法
阚琳洁,张建国,邱继伟
(1. 北京航空航天大学 可靠性与系统工程学院, 北京 100191;2. 北京航空航天大学 可靠性与环境工程技术重点实验室, 北京 100191)
在航空航天、机器人、汽车、舰船等诸多行业中,柔性机构都具有举足轻重的地位,近几年来备受人们的关注[1-2]。在大多数实际工程问题中,柔性机构的系统参数如材料性能、几何形状、刚度、阻尼系数、制造公差等都具有随机性,使得柔性机构可靠性问题尤为重要。对于柔性机构时变可靠性分析问题,传统且有效的方法是利用经典的结构时变可靠性理论建立极限状态函数,采用Monte Carlo仿真分析(MCS) 、解析法[3]或上穿率法[4]。然而,由于其系统动力学方程的非线性、耦合、时变特征,一次模型的计算量通常是相当高的,采用MCS法计算效率会很低。而且极限状态函数在非线性影响下难以显示化表达,使得解析法和上穿率法也难以实施[5]。因此,一些学者开始研究基于代理模型的柔性机构时变可靠性分析技术,并取得了一定的成果,例如响应面[6]、神经网络[7]、支持向量机[8]、混沌多项式(Polynomial Chaos Expansion,PCE)[9]等。
由Wiener[10]提出的混沌多项式是一种正交展开方法,标准正交函数系由Hermit基函数构造。Liu等[11]对其进行了扩展,提出了基于Askey-scheme正交基的广义混沌多项式(Generalized Polynomial Chaos,GPC),常用于随机系统的建模、不确定性传播和量化、以及求解任意概率分布的随机微分方程等方面。作为新兴的代理模型技术,GPC属于随机数学模型。相较于其他代理模型,GPC不受拟合点位置的影响,近似精度高,并且可以获得系统响应精确解的全部信息[12],但应用于柔性机构时变可靠性分析的研究成果较少。Guo等[13]利用GPC的非侵入式算法结合模糊概率理论,提出了考虑固有-认知混合不确定信息的机构运动可靠度分析方法。并利用移动最小二乘法来近似表达时变GPC系数的变化趋势,提出了考虑磨损的机构时变全局灵敏度分析法,以及考虑磨损的机构运动的时变可靠性优化设计方法[14]。赵宽[15]利用基于PCE的随机响应面法,对随机参数旋转柔性梁和双连杆机械臂进行了机构性能(运动、强度、刚度)的静态可靠性分析。虽然混沌多项式模型计算精度高,但是系统随机参数数量多,刚柔耦合引起的非线性问题,以及系统结构的复杂性,会使得混沌多项式理论用于时变可靠性分析时计算成本迅速增长。
综上所述,柔性机构的系统动力学模型一般为具有时变、高非线性、强耦合特征的微分方程组,其系统可靠性问题同时具有时变耦合的特点。传统的柔性机构可靠性分析方法不仅难以描述柔性机构的时变耦合特征,而且模型精度差、计算效率低。为了提高计算效率,描述柔性机构在刚柔耦合影响下的时变可靠性特征,本文提出基于模态综合法(Component Mode Synthesis,CMS)和GPC的时变随机响应面法。建立了柔性机构时变可靠性分析的随机代理模型,并用MCS法进行系统运动时变可靠度求解。
1 柔性机构动力学的随机场离散和模型降阶
1.1 随机场离散
考虑机构系统的材料特性与几何尺寸的随机性,基于混合坐标法,利用有限元法对柔性体的变形进行描述,结合拉格朗日方程可推导出如下形式的柔性机构系统动力学的随机模型[16]
(1)

如前所述,柔性机构的材料特性参数具有不确定性,并在空间域中连续变化,可用随机场进行描述。设具有协方差函数C(x1,x2)的随机场可表示为h(x,θ),用Karhunen-Loeve展开法进行随机场离散可得[17]
(2)
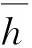
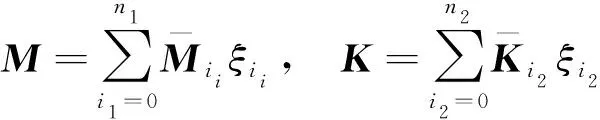
(3)
则有
(4)
1.2 动力学模型降阶的CMS法
采用有限元法对柔性体变形进行描述时,坐标数目庞大,动力学模型式(1)为非线性、耦合的微分方程组。为了提高计算效率,本文采用CMS法对刚柔耦合动力学模型进行降阶,并且假设柔性体模态为确定性模态[18]。在模型降阶过程中暂不考虑刚体运动的影响,仅对柔性体的弹性变形进行降阶,其动力学方程为
(5)

(6)
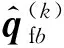
(7)
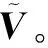
(8)
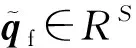
(9)
降阶后的柔性体运动方程可表示为
(10)

(11)

(12)

(13)
式中:Ξ∈RD×H为正交化的CMS模态矩阵。利用均值处的模态矩阵对随机动力学模型式(4)进行降阶,则广义坐标q的正交投影变换可以写为
(14)

(15)
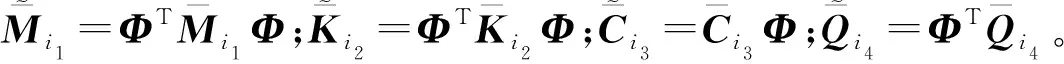
2 基于CMS-GPC的时变随机响应面
2.1 时变随机响应面
利用GPC模型可以有效地对系统响应的随机特征进行描述,并具有显示化和线性化的作用,但是GPC对系统模型也产生了一定的扩阶影响,广义坐标q的自由度从RC扩展到RC·(M+1)。为了提高计算效率,本文将CMS方法与GPC方法相结合,提出时变随机响应面的随机代理模型。
(16)
式中:t∈[0,T];{Ψj(ξ),j=0,1,2,,M}为随机函数空间中的Askey-scheme正交基,且Ψ∈R(6+H)×[(6+H)·(M+1)],ξ=(ξi1,ξi2,,ξin)为N维随机向量,a(t)∈R(6+H)·(M+1)为多项式时变系数,M为截断系数。若Askey-scheme正交基的最高阶次为p,则最高阶次p、随机向量维数N和截断系数M满足如下等式关系
(17)
对应不同分布类型的Askey-scheme正交基如表1所示。

表1 对应不同分布类型的Askey-scheme正交基Tab.1 Askey-scheme for selecting polynomials corresponding to certain types of distributions
任意两个Askey-scheme正交基之间满足
(18)
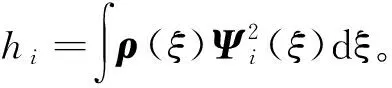
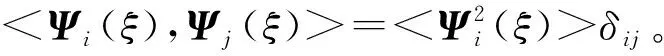
(19)
其次,根据式(14)和式(16),系统广义坐标q可以写为两级正交展开变换形式

(20)
也可以写为如下截断形式
(21)

(22)
原GPC模型计算问题的大小从C·(M+1)下降到(6+H)·(M+1),其中(6+H)< 用Λ(ξ)对式(4)进行Galerkin投影,可得 整理可得 (23) 则式(23)为M+1个确定性的二阶微分方程,可求得时变随机响应面的时变系数a(t)。 (24) (25) (26) 在时间[0,T]内,运动精度的时变累积失效概率为 Pf,c(0,T)=Pr(∃t∈[0,T]|G(ξ,t)≤0) (27) 在建立柔性机构时变可靠性模型的基础上,采用MCS法进行时变可靠性分析。将时间离散成N个时间点,每个时间间隔为Δt=T/(N-1),对应的响应面G(ξ,t)离散成{G(ξ,ti),ti=(i-1)Δt且i=1,2,,N},则在时间[0,ti]内运动精度的时变累积失效概率为[19] (28) 式中:NMCS为总的仿真次数;Nj,fature为在时间[ti,ti+1]内系统失效的次数。 归纳上述基于CMS-GPC的柔性机构时变可靠性建模分析过程,给出如下分析步骤: 步骤1确定系统随机参数的分布类型。对高斯随机场可采用可以通过 Karhunen-Loeve 展开转化成离散的标准随机向量。 步骤2建立柔性机构动力学模型,依据步骤1对随机参数的处理,将动力学模型进行随机展开,形式如式(2),并确定模型的初始条件。 步骤3求解模态降阶矩阵Φ。采用CMS法对刚柔耦合动力学模型进行降阶,并且假设柔性体模态为确定性模态,得到均值处的模态降阶矩阵Φ。 步骤4确定GPC模型中正交基Ψ的阶次p和截断系数M,建立系统响应的时变随机响应面q(ξ,t)=ΦΨ(ξ)a(t)=Λ(ξ)a(t)。利用Galerkin投影法求解响应面的时变系数,分析系统响应的时变均值和时变方差。 步骤5基于时变随机响应面,建立系统运动精度的时变可靠性模型,并利用MCS法求解时变可靠度。 以两连杆柔性机械臂为例,对本文提出的方法进行验证。图1为两连杆柔性机械臂示意图,在空间零重力环境下做平面大范围运动,初始状态为水平位置,无变形,无初始速度和加速度。 图1 两连杆柔性机械臂Fig.1 Two-link flexible manipulator 组成机械臂的杆1和杆2为均质的Euler-Bernoulli梁,横截面均为矩形,服从正态分布,相关参数由表2给出。臂杆长度为L1=L2=1.5 m,作用在臂杆上的驱动力矩分别为τ1(t)=60sin2(2πt)+25,τ2(t)=50sin2(2πt+0.5)+15。关节处集中质量为m1=10 kg,杆2末端负载集中质量为m2=5 kg。机械臂的材料参数服从正态分布,相关参数由表3给出。 表2 两连杆机械臂横截面参数Tab.2 Section sizes of two-link flexible arm 表3 两连杆机械臂材料参数Tab.3 Material parameters of two-link flexible arm 两臂杆各离散5个单元,建立两连杆柔性机械臂动力学模型,并利用式(2)~式(4)进行随机场离散。其次,杆1和杆2分别取前两阶模态,建立两连杆柔性机械臂末端X方向位移x(ξ,t)和Y方向位移y(ξ,t)的时变随机响应面模型,取Λ(ξ)的最高阶次为4阶,根据式(17)则响应面的截断系数为210。 (29) 图2和图3分别给出了两连杆柔性机械臂末端X方向位移的均值和均方差随时间变化的规律,并与Monte-Carlo模拟105次的计算结果进行对比,时变均值的最大相对误差为0.17%,时变方差的最大相对误差为0.56%,误差较小,具有较高的拟合精度。 图2 机械臂末端X方向位移均值Fig.2 Mean displacement of the end node in X direction 图3 机械臂末端X方向位移方差Fig.3 Displacement covariance of the end node in X direction 图4和图5分别给出了两连杆柔性机械臂末端Y方向位移y(ξ,t)的均值和均方差随时间变化的规律。同样与Monte-Carlo模拟105次的结果相比,时变均值的最大相对误差为0.17%,时变方差的最大相对误差为0.56%,同样误差较小,说明本文所提出的时变耦合响应面具有较高的计算精度。同时,计算规模与仅用GPC模型相比,减小了80%。 图4 机械臂末端Y方向位移均值Fig.4 Mean displacement of the end node in Y direction (30) Y方向运动精度的时变极限状态函数为 (31) 在此基础上,采用MCS法计算计算X方向和Y方向定位精度的时变累积失效概率。图6和图8分别为X方向和Y方向的累积失效概率在0~2 s内的变化趋势,并且与MCS仿真105次进行了结果对比,其相对误差随时间的变化趋势如图7和图9所示。从结果来看,与仅用MCS法相比,累积失效概率的变化趋势相同。其中X方向累积失效概率的最大相对误差为0.75%,Y方向累积失效概率的最大相对误差为0.76%,故误差结果在可接受范围内,说明本文提出的方法是可行的。 图6 机械臂末端X方向定位精度累积失效概率图7 末端X方向累积失效概率的相对误差图8 机械臂末端Y方向定位精度累积失效概率图9 末端Y方向累积失效概率的相对误差Fig.6 The cumulative failure probability of the positioning accuracy of the end node in X directionFig.7 The relative error of the cumulative failure probability of the end node in X directionFig.8 The cumulative failure probability of the positioning accuracy of the end node in Y directionFig.9 The relative error of the cumulative failure probability of the end node in Y direction (1)本文针对柔性机构系统时变可靠性分析的“时变耦合”问题,提出了基于CMS-GPC的时变随机响应面模型,在保证拟合精度的同时,降低了计算问题的规模,提高了效率。其次,与传统时变可靠性分析的响应面模型不同的是,本文所建立的时变随机响应面模型是描述系统随机响应特征的,而非对特定时间下极限状态函数的拟合。 (2)在时变随机响应面基础上,可直接建立显示化的柔性机构运动时变可靠性模型,并给出了计算运动精度时变累积失效概率的MCS方法。与传统时变可靠性分析方法相比,本方法不需要在设计验算点处对特定时间下的极限状态函数重复建立响应面,因此提高了计算效率。 (3)通过两连杆柔性机械臂的案例对本文的方法进行了可行性和有效性验证,计算精度与MCS法相差无几,对工程应用具有一定的指导意义。2.2 时变随机响应面的时变系数求解
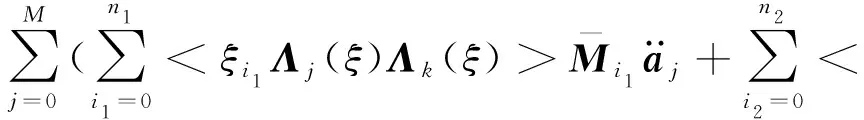
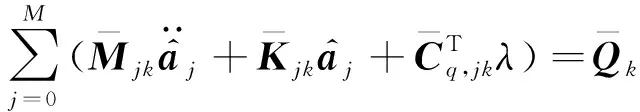

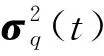
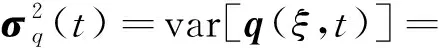
3 柔性机构时变可靠性分析
3.1 时变可靠度计算方法
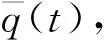
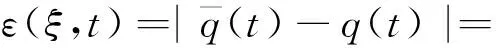
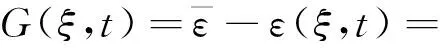
3.2 柔性机构时变可靠性分析流程
4 案例分析
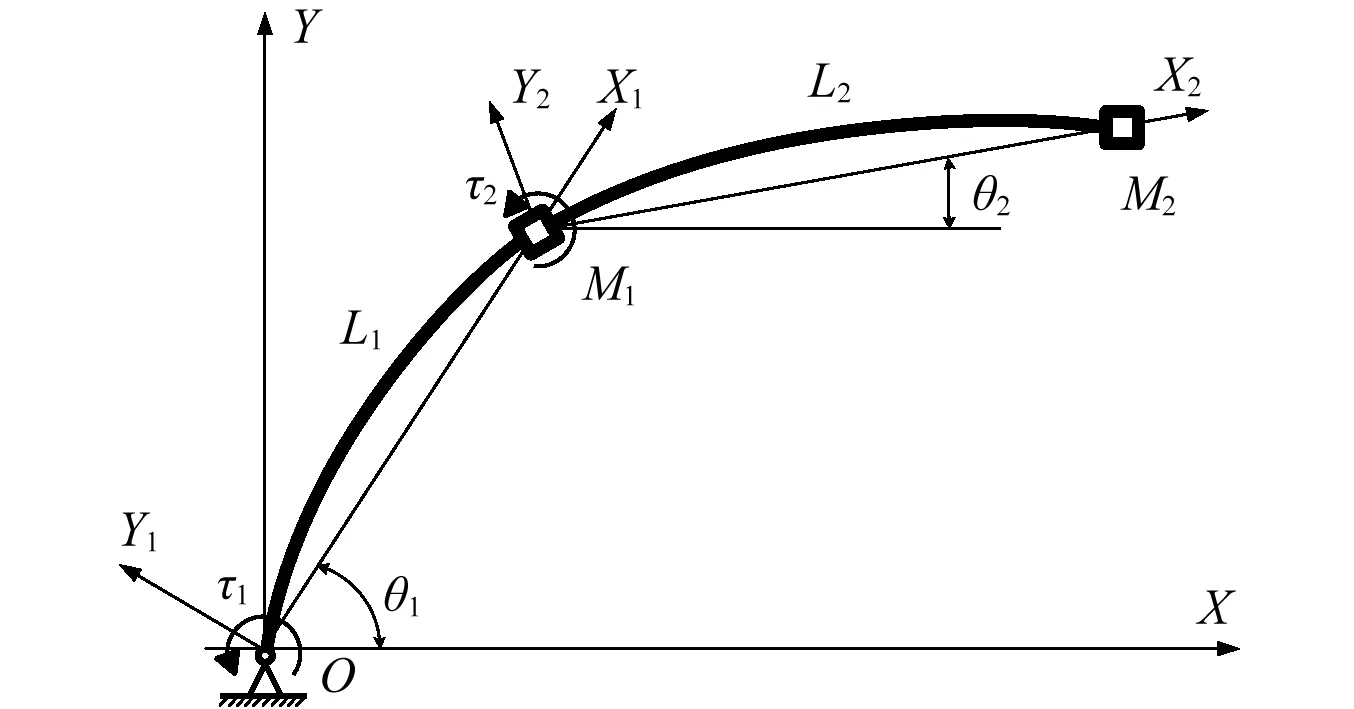








5 结 论

