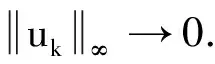在部分次线性情形下 Schrödinger系统无穷多解的存在性

孟亚君， 冯晓晶

(山西大学 数学科学学院，山西 太原 030006)

0 引言

文中讨论一类Schrödinger-Poisson系统解的存在性和多重性：

(1)

其中位势函数V满足如下假设：

(V)V∈(R3,R)，infR3V>0且存在一个常数r0>0，使得对于任何M>0，

lim|y|→∞meas{x∈R3:|x-y|≤r0,V(x)≤M}=0,

其中meas(·)表示R3中的Lebesgue测度.

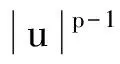
另一方面，文献[3]研究了非径向解的情况. 在文献[4]中，当u趋于无穷，f(x,u)满足超线性条件下，Seok证明了(1)有无穷多个高能解. 在文献[5]中，Sun研究了如下系统

(2)

解的存在性，并得到了下面的定理:

定理A[5]假设如下条件成立:

A1)V∈(R3,R)且infx∈R3V(x)≥β>0；

A2)对每一个M>0，有meas{x∈R3:V(x)≤M}<∞；

则(2)有无穷多解.

在这个定理中，类似F(x,u)的特殊情况，许多超线性函数在数学物理学中不满足(A3). 随后，作者运用临界点理论，通过减弱条件(A3)来推广定理A，并获得了如下定理.

定理B[6]假设V和f满足(A1)，(A2)和下列条件：

B1)f∈C(R3×R，R)且存在常数列1<γ1<γ2<…<γm<2和函数列ai∈L2/(2-γi)(R3，[0，∞))，i=1,2,…,m，使得

B2)存在一个开集Λ⊂R3和三个常数δ>0，γ0∈(1,2)且η>0使得

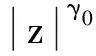
B3)f(x,-z)=-f(x,z)，(x,z)∈R3×R.

则(2)有无穷多个解.

最近，作者得到了Clark定理的推广定理如下.

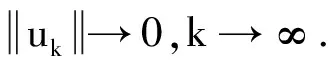
1 主要结论

文中将用定理C来推广定理A和B. 主要结论如下:

定理1 假设f满足(B3)及以下条件：

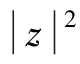
f3)K:R3→R+是一个正连续函数，使得K∈L2/(2-γ)(R3)∩L∞(R3).

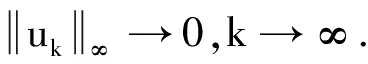
注1 显然，由条件B2)知条件f2)和f1)比条件B1)弱.

注2 整篇文章中，我们用C>0表示不同的正常数.

2 预备知识

这一部分将给出这篇文章中用到的一些记号和引理.

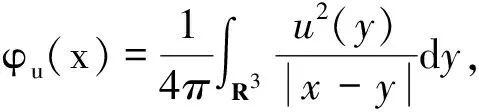
引理1[8]下面性质成立：

i)存在C>0使得对任何u∈H1(R3)，

ii)对于任意u∈H1(R3)，都有φu≥0；

iii)如果u是径向对称的，则φu是径向的；

iv)对于任意的t>0和u∈H1(R3)，φtu=t2φu.

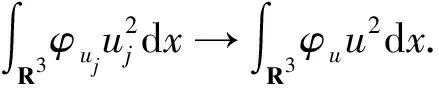
3 主要结论的证明

(3)

易知系统(3)是变分的，并且它的解为定义在E上的泛函

的临界点. 由(f1)，易知J在E上有定义且J∈C1(E,R)(更多细节见文献[6])，并且有

注意到J是偶函数，且J(0)=0. 对于u∈E，我们有

(4)

现在将用同样的思路证明泛函J满足(PS)条件. 若{un}是E中的一个序列，使得J(un)有界且J′(un)→0，则将证明{un}有一个收敛子列. 由(4)可知{un}在E中有界，不失一般性，假设{un}在E中弱收敛到u，显然有

当n→∞时I1→0. 下面将估计I2，因为在L6(R3)中有φun→φu，且在L12/5(R3)中存在子列un→u，故得，

最后估计I3，通过运用条件(f3)，对于任意的R>0，有

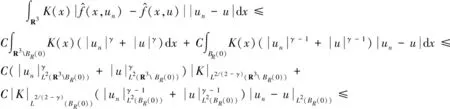
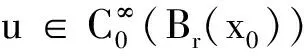
supXk∩SρkJ(u)<0，

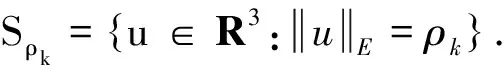
(5)