具有积分边界条件的二次奇摄动边值问题
王丹丹, 谢 峰
(东华大学 理学院, 上海 201620)
奇异摄动问题一直受到学者们的广泛关注, 利用微分不等式理论、平均化理论、边界层理论以及其他理论研究了不同类型的奇摄动边值问题[1-7], 解决了许多数学、物理及生物问题。 其中, 二次奇异摄动问题一般指二阶微分方程中一阶导数项为二次, 来源于催化表面化学反应的Weekman-Goring模型[4]。 Chang等[2]用微分不等式方法研究了几类二次奇摄动Robin边值问题的边界层现象。Kelly[3]研究了如下二次奇异摄动问题:

其中,0<ε≪1, 在相对较弱的条件下, 给出其解的渐近估计。
近年来,含有积分边界条件的奇摄动微分方程应用于各种物理问题, 得到了一些关于解的存在性和唯一性问题的结论, 并发展了各种数值方法。例如文献[8-9]利用边界层函数法研究了几类具有积分边界条件的非线性奇摄动问题。
受到以上工作的启发, 本文将研究如下具有积分边界条件的弱二次奇摄动边值问题:

(1)

(2)

(3)
式中:ε>0。
作如下假设:
(1)[H1]b(t,x)≥k>0, 对任意t∈[0,1],x∈R都成立;
(2)[H2]退化问题
(4)

(5)
在[0,1]上有唯一连续可微的解;
(3)[H3] 函数a(t,x)、b(t,x)、c(t,x)关于x,t连续可微,hi:R→R均为连续函数,hi(0)=0, 存在正数ki(i=1,2)有k1+k2<1。σi为(0,∞)→(0,∞)上的连续非减函数, 满足σi(u)≤kiu,u>0, 且有|hi(y)-hi(z)|≤σi(y-z), ∀y,z∈R,i=1,2。
1 构造渐近解
借助合成展开法[5], 设问题(1)~(3)具有如下形式渐近解:
(6)

1.1 正则部分
由假设可知,V0(t)由退化方程式(4)~(5)决定, 且V1(t)满足如下方程:

或者写成如下形式:
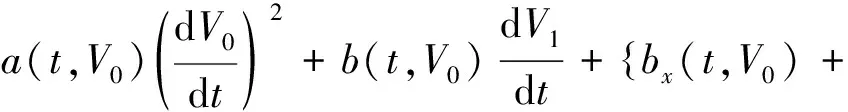
(7)
式中:V0(t),V1(t)分别满足边界条件:

(8)

(9)
1.2 校正项

将上式代入式(1), 则Q(τ)满足微分方程:
即有
(10)
将式(10)两边关于ε泰勒展开并比较等式两边ε的系数,可得边界层项Q0、Q1和Q2分别满足:
(11)
c(0,V0(0)+Q0)=0
(12)

(13)
为简单起见,将式(12)和(13)写成如下形式
(14)
(15)
则Q0、Q1和Q2应满足的边界条件为

(16)
(17)
(18)
由式(10)、(15)和(17)可知Q0(τ)的隐式表达式为
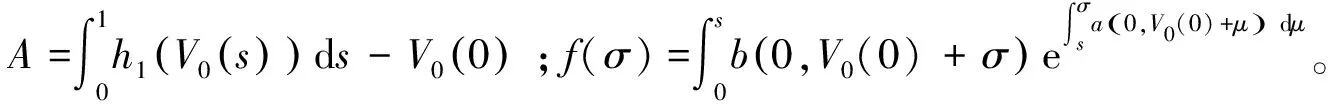
由假设[H3]知存在正常数C1和C2,使得式(19)成立[2]。
C1e-kt/ε≤|Q(τ)|≤C2e-kt/ε
(19)
为简单起见,将式(14)改写为
即有

(20)
由于Q0呈指数衰减, 式(20)等号右端收敛, 利用常数变易公式可得

由于Q0呈指数衰减, 则Q1呈指数衰减[5], 同理易知Q2也呈指数衰减。
由此得问题(1)~(3)的形式渐近解为
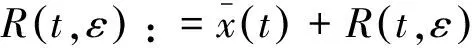


式中:N为充分大的正数。
2 主要结论及证明
引理2.1(不等式理论[9])假设条件[H3]成立, 在[0,1]上存在两个函数α(t)和β(t),其中,α(t)≤β(t),且分别满足不等式:
和
则边值问题(1)~(3)存在一个解x(t),使得
α(t)≤x(t)≤β(t),t∈[0,1]
且当α(t)和β(t)满足上述条件时, 分别称为问题(1)~(3)的上下解。
定理2.2假设[H1]~[H3]成立, 则边值问题(1)~(3)存在解x(t), 且当ε→0时,在[0,1]上有
证明由解的构造及假设[H1]~[H3]知存在正数M和L使得

选取辅助函数
满足
令

由α(t)和β(t)的定义显然有

及


同理可得

由引理2.1可知问题(1)~(3)存在一个解x(t)满足α(t)≤x(t)≤β(t)。 定理2.2证毕。
3 例 子
考虑如下具有左边界层的奇摄动问题:

其精确解为
其中,c1和c2满足
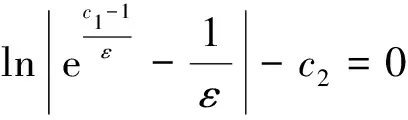
由渐近解的构造可得其零阶近似解为
或
即关于ε的渐近展开和形式渐近解完全一致。

