基于Pair Copula-Realized GARCH模型的股票市场

李嘉琪，何 坤

(东华大学 理学院， 上海201620)

随着经济的快速发展，金融改革创新不断推进，金融市场的波动和投资风险逐渐加大，市场之间的关系也越来越复杂。构造多种资产投资组合可以有效地在金融市场上规避风险，获得投资收益，因此金融资产间的相关结构以及波动影响也就成为了值得研究的方向。在真实的金融市场环境中，资产收益率曲线大多呈现出尖峰厚尾，尾部呈现非线性以及波动聚集等特征形态，这就使得传统模型中的正态和线性相关等基本假设无法满足实际的情况。

为了更好地研究相关结构关系，Sklar[1]提出了Copula函数的概念，指出了Copula函数可以连接各个边缘分布及其联合分布，打破了以往只能分析线性相关的局限性。即Copula函数能够很好地用来刻画非对称和非线性相关结构，这与传统模型相比有着明显优势。Nelson[2]对Copula函数继续研究，总结了Copula函数族并进行了相关应用。Embrechts等[3]利用Copula函数进行了金融风险分析。在此之后Copula函数理论开始被广泛地应用于各个金融领域的研究之中。Huang等[4]结合了Copula函数与GARCH模型的特点，计算了投资组合的风险价值(value at risk， VaR)，并将其应用到研究NASDAQ和TAIEX指数之中去。Aas等[5]提出了对多元Copula函数进行降维分解的Pair Copula方法，即把多元变量的联合分布函数转化为基于二元条件Copula函数与各自边缘分布函数的乘积，为多种投资组合的研究提供了理论基础。

同时为了解决时间序列条件异方差性的问题，Engle[6]率先提出了ARCH(autoregressive condition heteroskedasticity)模型，并被广泛应用于金融市场的分析决策中。Bollerslev[7]以ARCH模型为基础，提出了GARCH(generalized autoregressive condition heteroskeclasticity)模型，描述了市场波动的异方差性和波动集群性。但是GARCH模型仅停留在低频层面上，未包含日间数据的信息，而高频的数据则可以提供更多的信息。Engle[8]后来直接将含有高频信息的外生变量引入到GARCH模型中，构造出了GARCH-X模型，这种模型特点是简单直观，但是无法进行多步预测。Hansen等[9]提出了Realized GARCH(p,q)模型，以解决高频信息的问题，通过引入测度方程，将收益率、条件波动率和已实现测度三者联合建模，从而使投资决策和预测更为精确。

目前将Copula或Pair Copula函数与低频GARCH类模型结合以解决具体问题的研究[10-13]已经相对成熟和完善，但是对于Realized GARCH的研究较少。例如：Solibakke[14]用Realized GARCH模型研究不同频率的高频数据，用半似然函数法(QML)拟合期货合约。Watanabe[15]基于Realized GARCH模型预测了VaR和ES(expected shortfall)。黄雯等[16]用高频数据预测沪深300的指数波动率，发现在预测效果上Realized GARCH模型相比传统GARCH模型有很大改善。黄友珀等[17]利用Pair Copula-Realized GARCH进行了资产组合收益分位数预测的研究。本文将基于Pair Copula-Realized GARCH对股票市场相关性和波动进行分析以及数据研究。

1 Copula函数及Pair Copula分解

1.1 Copula函数

Copula函数是由Sklar[1]在1959年提出的，他发现任意一个多维随机变量的联合分布函数可以被分解成一个Copula连接函数以及多个边缘分布函数，其中边缘分布函数服从(0,1)上的均匀分布。Copula函数的优势在于能够将多个随机变量的边缘分布连接起来，最终得到它们的联合分布，不需要每个变量的边缘分布相同，这与传统方法相比具有很好的灵活性。

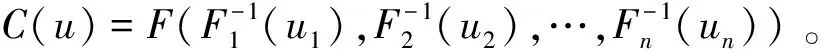
f(x1,x2,…,xn)=c(F1(x1),F2(x2),…,Fn(xn))·

f1(x1),f2(x2),…,fn(xn)

常用的Copula函数分为两类: 椭圆Copula函数和阿基米德Copula函数。椭圆Copula函数主要有正态-Copula函数和t-Copula函数，两者均有对称的尾部相关性，因此只能适应对称的相关结构。阿基米德Copula函数主要有Gumbel Copula、Clayton Copula和Frank Copula。Cumbel Copula函数适合描述上尾部分的相关性，Clayton Copula函数适合描述下尾部分的相关性。而对于Frank Copula函数，由于其上尾和下尾相关系数均为零，多应用于具有对称关系的金融市场模式上。常见Copula函数的分布如表1所示。

表1 常见的Copula函数分布Table 1 The common distribution of Copula function

1.2 Pair Copula分解

在研究多种投资组合收益之间的相关性时，发现中间的结构特别复杂，如果直接用多元Copula函数来构造组合结构，效果并不是很理想。因此，Aas等[5]提出了对多元Copula函数进行降维的Pair Copula分解法。

通常用来构建Pair Copula模型的两种藤结构分别是C-Vine和D-Vine，其结构图分别如图1和2所示。C-Vine结构呈树冠状，藤树Tj的根节点衍生出的每条边对应一个Pair Copula函数，可以选择与其他变量相关性最强的作为关键点。D-Vine结构是线性的，每个节点与其他节点相连接数最多为2，藤数Tj有(5-j)个节点和(4-j)条边，每条边对应一个Pair Copula函数。

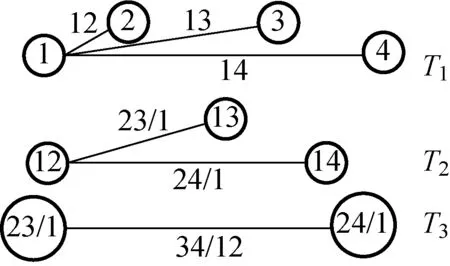
图1 C-Vine结构图Fig.1 Structure of C-Vine

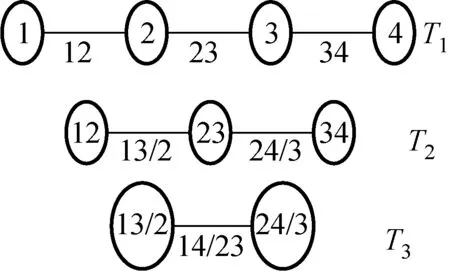
图2 D-Vine结构图Fig.2 Structure of D-Vine

四维结构的C-Vine和D-Vine分解表达式为

C-Vine:

f(x1,x2,x3,x4)=f1(x1)f(x2)f3(x3)f4(x4)×

c12(F1(x1),F2(x2))×c13(F1(x1),F3(x3))×

c14(F1(x1),F4(x4))×c23|1(F(x2|x1),

F(x3|x1))×c24|1(F(x2|x1),F(x4|x1))×

c34|12(F(x3|x1,x2),F(x4|x1,x2))

D-Vine:

f(x1,x2,x3,x4)=f1(x1)f2(x2)f3(x3)f4(x4)×

c12(F1(x1),F2(x2))×c23(F2(x2),F3(x3))×

c34(F3(x3),F4(x4))×c13|2(F(x1|x2),

F(x3|x2))×c24|3(F(x2|x3),F(x4|x3))×

c14|23(F(x1|x2,x3),F(x4|x2,x3))

在对Pair Copula函数作最优选择时，通常采用赤池信息量准则(Akaike information criterion,AIC)和贝叶斯准则(Bayesian information criterion, BIC)作为拟合检验判别标准。AIC和BIC都引入了与模型参数个数相关的惩罚项，并且BIC的惩罚项比AIC的多考虑了样本数量的因素。当样本数量过多时，BIC可有效防止模型精度过高造成的模型复杂度过高。

AIC和BIC的表达式分别为:PAIC=2K-2lnL，PBIC=Kln(n)-2lnL，其中，K是模型的参数个数，L是被估计模型的似然函数的最大值，n是样本数量。

2 Realized GARCH模型

Hansen等[9]在2011年提出了Realized GARCH(p,q)模型，其主要思想是在GARCH模型的基础上，加入高频数据的信息，可以得到更好的拟合效果和模型解释能力。通过引入测度方程，把收益率、条件波动率和已实现测度三者进行联合建模。

Realized GARCH(p,q)模型的一般表示形式为

(1)

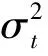
本文在后续的研究分析中将采用Realized GARCH(1,1)的对数形式进行建模，其表达式为

(2)

此外，基于Realized GARCH模型对高频数据进行建模时，需要计算已实现测度。 本文将采用最简单的已实现波动率(realized variance， RV)进行定义，表达式为

式中：rt,i是日内收益率；m与采样频率有关。如果采样频率为1 min，在一天的交易时间段(9: 30-11: 30)和(13: 00-15: 00)，则m=240；如果采样频率为5 min，则m=48。

3 股票市场的数据分析

3.1 数据选取

本文选取了上证指数、深证成指、中小板指和创业板指的数据，包括日收益率和5 min高频数据，数据时间从2014年1月1日开始到2016年12月15日结束，并使用R语言和Matlab软件进行数据操作处理。

3.2 Pair Copula-Realized GARCH 模型构建

(1)选用Realized GARCH模型分别对每个对数收益率序列进行拟合，消除数据的自相关性和不平稳性，得到独立的标准化残差序列。

(2)对标准化残差序列进行核分布估计变换，来构造新的残差序列。同时检验变换之后的数据是否服从(0,1)间的均匀分布，使其满足Pair Copula函数的基本条件。

(3)选择藤结构模型(C-Vine和D-Vine)，用极大似然法进行Pair Copula的参数估计，根据信息准则AIC/BIC，选出最优的Copula函数来描述变量间的关系，从而确定多个收益率构成的联合分布。

3.3 数据分析

将价格Pt定义为每日指数收盘价，则第t日的对数收益率为rt=ln(Pt/Pt-1)。对上证指数、深证成指、中小板指和创业板指的对数收益率序列进行描述性统计，结果如表2所示。

这4个指数的对数收益率序列峰度均大于3，偏度小于0，因此呈尖峰厚尾的形态。J-B统计量也表明这4个指数均不服从正态分布。同时，这4个指数的对数收益率频数直方图如图3所示，也能很直观地看出各指数分布非正态的性质。

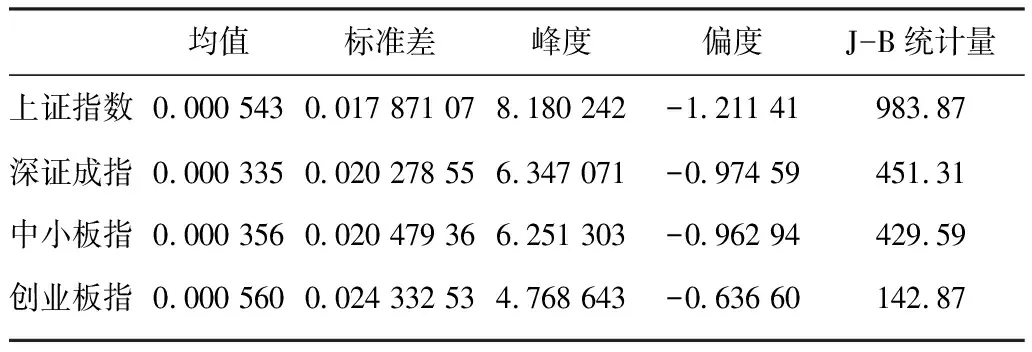
表2 4种指数的描述性统计Table 2 The descriptive statistics of four indexes

(a)上证指数

(b)深证成指

(c)中小板指

(d)创业板指图3 上证指数、深证成指、中小板指和创业板指日对数收益率频数直方图Fig.3 The daily log return frequency histogram of Shanghai composite index, Shenzhen component index, small and medium-size board index and second board index

为了防止出现数据伪回归性的问题，先用ADF(Augmented Dickey-Fuller)检验法对4种指数对数收益率序列进行平稳性检验，结果如表3所示。由表3可知，数据在1%的显著水平下呈现平稳趋势，不存在单位根。

表3 4种指数的平稳性检验Table 3 Stationarity test of four indexes

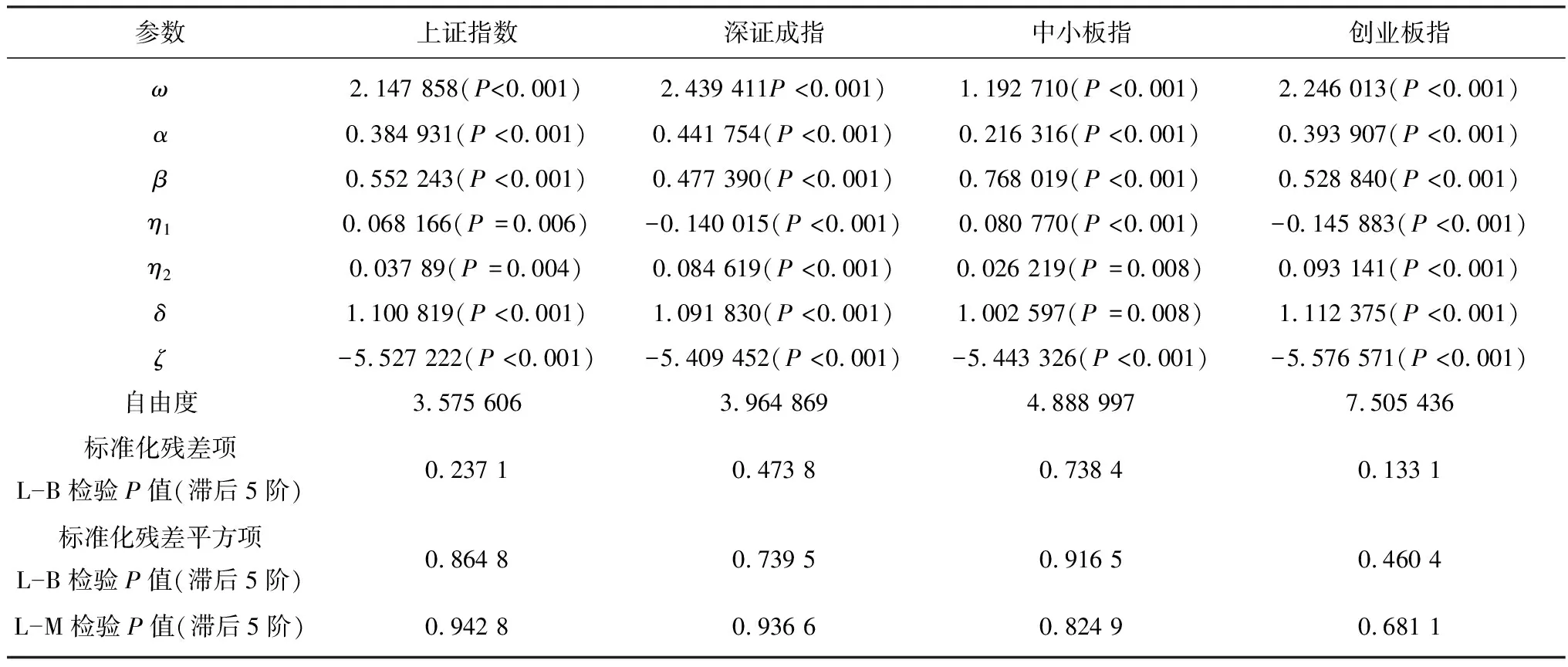
表4 Realized GARCH模型的参数估计Table 4 Parameter estimation of Realized GARCH model

由表4可知，模型中每个估计参数值的P值均小于0.01，表明这些参数值都是显著的，并且标准化残差项和标准化残差平方项在5%显著水平下均通过白噪声检验，说明模型可靠。同时建模后的数据也通过了ARCH L-M检验，说明数据不存在自相关的ARCH效应。

为了使得数据落在Copula函数自变量定义域范围内，对模型取得的标准化残差进行核分布估计变换。对变换后得到的新序列进行K-S检验，得到的P值分别是0.648、0.812、0.949、0.907，表明新序列服从(0,1)之间的均匀分布，可以对其进行Pair Copula建模。

4个指数的Kendall秩相关系数如表5所示。由表5可知：上证指数与中小板指显著正相关，相关系数为0.611，说明当上证指数出现大幅度涨或跌的波动时，中小板指数也容易受其影响做出相应反应；深证成指则与创业板之间也有相关性，相关系数为0.565。

表54个指数的Kendall秩相关系数

Table5Kendallrankcorrelationcoefficientoffourindexes

股票上证指数深证成指中小板指创业板指上证指数1.0000.0240.6110.008深证成指0.0241.0000.0120.565中小板指0.6110.0121.0000.025创业板指0.0080.5650.0251.000

再根据AIC/BIC准则选取最优的Copula函数。同时为了分析不同的Pair Copula结构对于多个指数相依性的拟合效果，分别对C-Vine和D-Vine 结构进行比较。在这里使用R语言的CD-Vine 程序包进行计算，配对出相应的Copula函数和参数，Copula函数的参考范围设定在Gaussian Copula、t-Copula、Clayton Copula、Gumbel Copula和Frank Copula之中，结果如表6所示。

表6 C-Vine 和D-Vine结构下的Copula 函数参数Table 6 Parameters of Copula function on C-Vine and D-Vine

由表6可知：在C-Vine结构下，两种准则值分别为-1 519.437和-1 473.617；在D-Vine结构下，两种准则值分别为-1 513.043和-1 471.805。由此可以说明，C-Vine的结构将更加适合于分析这4个指数之间的关系。

4 结 语

本文基于Pair Copula-Realized GARCH模型对股票市场进行了研究，在低频数据的基础上引入已实现波动测度方程，能够提取高频数据的信息。同时，对于多种资产结构，用Pair Copula分解法进行降维建模，可以更加精准地描述出股票市场间的关系。

研究后所得出的结论是: (1)上证指数、深证成指、中小板指和创业板指这4个有代表性的对数收益率曲线均符合金融市场上非正态，呈“尖峰厚尾”的特点，且存在一定的相关性；(2)使用Realized GARCH模型可以为高频数据消除异方差的干扰，建模后的标准化残差没有ARCH效应，接受白噪声检验；(3)对建模后的标准化残差进行核分布估计变换，再对变换后的序列进行Pair Copula降维，用C-Vine和D-Vine结构分别建立指数间关系，并用AIC和BIC准则进行比较，发现C-Vine的结构比D-Vine更加适用于拟合4个指数间的相关结构。