阶乘幂方法在解非齐次差分方程中的应用
孙建新
(绍兴文理学院 数理信息学院,浙江 绍兴 312000)
参考文献[1]研究了拟初等函数,参考文献[2]研究了函数展开为阶乘幂级数的方法.文献[3]在文献[1]和[2]的基础上,提出解齐次差分方程的新方法,即“阶乘幂方法”,并且对常系数齐次差分方程给出一般的解法与实例.本文将对常系数非齐次差分方程给出一般的新解法,同时给出相应的典型实例.不难发现,新方法具有计算简单、特解直观的优点.
1 几个引理
引理1.1 当特征根μ1,μ2,…,μk为k个互不相同的实根时,齐次方程
xn+k+b1xn+k-1+…+bk-1xn+1+bkxn=0
(1)
的通解为
(2)
引理1.2 当特征根μ1,μ2,…,μk为k个相同的实根μ(即为k重实根)时,齐次方程(1)的通解为
xn=c1μn+c2nμn+…+cknk-1μn=

(3)
其中P 引理1.3 齐次方程 xn+2-2axn+1+(a2+b2)xn=0 (4) 的通解为 (5) 亦即 xn=c1ancos! (hn)+c2ansin!(hn), (6) 其中 (7) 上述引理的证明参见文献[3],文中出现的新符号可参考文献[2][4][5]和[6]等. 引理1.4 若定义r2=a2(1+h2)(r>0)以及h=tanθ,则有 (8) (a+bi)n=(reiθ)n=rn{cos(nθ)+isin(nθ)}. 另一方面,由广义二项公式与拟三角函数定义又有 (a+bi)n=(a+ahi)n= an{cos!(hn)+isin!(hn)}. 比较两式的虚实部即得所证. 类似于三角函数的微分法则,有如下拟三角函数的差分法则: 引理1.5 若定义拟三角函数如式(7)所示,则 (9) 证明 获证. 注意到, (10) 可见,一般来说,普通三角函数的差分形式比较复杂,而拟初等函数的差分始终是简单的. 引理1.6 拟三角函数的高阶差分公式为 Δm{n!kcos!(hn)}= Δm{n!ksin!(hn)}= (11) 证明由文献[4]定理6.3等价表达式 Δm{f(n)g(n)}= 令f(n)=n!k,g(n)=cos!(hn)或sin!(hn),由引理1.4以及阶乘幂高阶差分公式 Δjn!k=k!jn!k-j,(j=0,1,…,k) 可知式(11)的第1式第一个等号成立.因为第二个等号相当于将和式按奇偶分类,不难验证其正确性,从略.又第2式与第1式是对称的,证明方法类同,不再重复. 特别地,对k=1或2以及m=1或2,有如下公式: 1)Δ{ncos!(hn)}= cos!(hn)-h(n+1)sin!(hn); 2)Δ{nsin!(hn)}= sin!(hn)+h(n+1)cos!(hn); 3)Δ{n!2cos!(hn)}= 2ncos!(hn)-h(n+1)!2sin!(hn); 4)Δ{n!2sin!(hn)}= 2nsin!(hn)+h(n+1)!2cos!(hn); 5)Δ2{ncos!(hn)}= -2hsin!(hn)-h2(n+2)cos!(hn); 6)Δ2{nsin!(hn)}= 2hcos!(hn)-h2(n+2)sin!(hn); 7)Δ2{n!2cos!(hn)}= 2cos!(hn)-4h(n+1)sin!(hn)- h2(n+2)!2cos!(hn); 8)Δ2{n!2sin!(hn)}= 2sin!(hn)+4h(n+1)cos!(hn)- h2(n+2)!2sin!(hn). 定理2.1 设常系数非齐次线性差分方程 xn+k+b1xn+k-1+…+bk-1xn+1+bkxn=q(n) (12) (13) 于是,由差分方程的线性性,而且移位算子E(或差分算子)是线性算子,所以有 Xn+k+b1Xn+k-1+…+bk-1Xn+1+bkXn= q(n)+0=q(n). 法则2.2 设k阶常系数非齐次线性差分方程形如 Δkxn+a1Δk-1xn+…+ak-1Δxn+akxn= P!m(n)(1+r)n,(r≠-1), (14) 其中 P!m(n)=bmn!m+bm-1n!m-1+…+b1n!1+b0. 若r为对应特征方程 λk+a1λk-1+…+ak-1λ+ak=0 的t重根(t=0,1,2,…),则其特解为 (15) 其中 Q!m+t(n)=cm+tn!m+t+cm+t-1n!m+t-1+…+ctn!t 为含m+1个参数的m+t次的阶乘幂多项式. 法则2.3 设k阶常系数非齐次线性差分方程形如 Δkxn+a1Δk-1xn+…+ak-1Δxn+akxn= (16) 其中 若 a+bi=r(cosθ+isinθ)=a(cos!h+isin!h) 与 a-bi=r(cosθ-isinθ)=a(cos!h-isin!h) 为对应特征方程 λk+a1λk-1+…+ak-1λ+ak=0 的一对t重共轭复根(t=0,1,2,…),则其特解为 或 其中 (j=1,2), 或 (j=1,2). 例1 求差分方程 xn+2-5xn+1+6xn=(n+1)2 的通解.(t=0) 解法1:对应特征方程为 μ2-5μ+6=0, 解得μ1=2,μ2=3. 则齐次方程的通解 因为1+r=1≠μj(j=1,2),t=0,m=2. 可设非齐次方程的特解为 {A(n+2)2+B(n+2)+C}- 5{A(n+1)2+B(n+1)+C}+ 6{An2+Bn+C}=(n+1)2. 虽然计算比较麻烦,仔细比较系数可得: 2A=1,-6A+2B=2,-A-3B+2C=1. 于是原差分方程的通解为 解法2:由定理1,原方程等价于方程 Δ2xn-3Δxn+2xn=n!2+3n!1+1, 对应特征方程为 λ2-3λ+2=0, 解得 λ1=1,λ2=2, 则齐次方程的通解 因为r=0≠λj(j=1,2),m=2,t=0.不妨设非齐次方程的特解为 则 2A-3(2An!1+B)+2(An!2+Bn!1+C)= n!2+3n!1+1. 比较系数易得 2A=1,-6A+2B=3,2A-3B+2C=1. 解得 于是原差分方程的通解为 显然两种解法的结果相同,而计算还是解法2简单. 例2 求差分方程 xn+2-2xn+1+xn=n2 的通解.(t>0) 解法1:对应特征方程为 μ2-2μ+1=0, 解得 μ1=μ2=1. 则齐次方程的通解 因为1+r=1=μj(j=1,2),t=2>0,m=2.可设非齐次方程的特解为 则 {A(n+2)4+B(n+2)3+C(n+2)2}- 2{A(n+1)4+B(n+1)3+C(n+1)2}+ {An4+Bn3+Cn2}=n2. 比较系数可得: 12A=1,24A+6B=0,14A+6B+2C=0. 于是原差分方程的通解为 解法2:由定理1,原方程等价于方程 Δ2xn=n!2+n!1, 对应特征方程为λ2=0,解得λ1=λ2=0. 则齐次方程的通解 因为r=0=λj(j=1,2),t=2,m=2,不妨设非齐次方程的特解为 则 比较系数易得 12A=1,6B=1,1C=0, 解得 于是原差分方程的通解为 例3 求差分方程 xn+2-2xn+1+2xn=n2n 的通解.(t=0) 解法1:对应特征方程为 μ2-2μ+2=0, 解得 μ1=1+i,μ2=1-i, 则齐次方程的通解 因为1+r=2≠μj(j=1,2),t=0,m=1,可设非齐次方程的特解为 则 2{A(n+1)+B}2n+1+2{An+B}2n=n2n. 比较系数可得: 2A=1,4A+2B=0. 解得 于是原差分方程的通解为 解法2:由定理1,原方程等价于方程 Δ2xn+xn=n2n. 对应特征方程为λ2+1=0,解得λ1=i,λ2=-i. 则齐次方程的通解 因为1+r=2≠1+λj(j=1,2),t=0,m=1.不妨设非齐次方程的特解为 则 比较系数易得 2A=1,4A+2B=0, 解得 于是原差分方程的通解为 由引理1.4的式(8),可知两种解法的结果相同.显然当m≥2时,求特解的计算一般是解法2简单,即阶乘幂方法较为简单. 例4 求差分方程 的通解.(t>0) 解法1:对应特征方程为 μ2-2μ+5=0, 解得 μ1=1+2i,μ2=1-2i, 则齐次方程的通解为 考虑到 cos!(2n)±isin!(2n), 比较实部、虚部有 因为r=1+2i=μ1,t=1>0,m=1.可设非齐次方程的特解为 (An2+Bn)(1+2i)n+(Cn2+Dn)(1-2i)n 则 {A(n+2)2+B(n+2)}(1+2i)n+2+ {C(n+2)2+D(n+2)}(1-2i)n+2- 2{A(n+1)2+B(n+1)}(1+2i)n+1- 2{C(n+1)2+D(n+1)}(1-2i)n+1+ 5{An2+Bn}(1+2i)n+5{Cn2+Dn} 比较系数可得: 解得 解法2:由定理1与引理1.4,原方程等价于方程 Δ2xn+4xn=ncos!(2n), 对应特征方程为 λ2+4=0, 解得 λ1=2i,λ2=-2i. 则齐次方程的通解 因为1+2i=1+λ1,t=1,m=1,并且方程无奇数阶差分,不妨设非齐次方程的特解为 则 B(n+1)!1}sin!(2n)+(2An+B)cos!(2n), -2{2A(n+1)+B}sin!(2n)+2Acos!(2n). 注意到(n+2)!2=n!2+4n!1+2,于是 {(-16A)n!1+(-6A-8B)}cos!(2n)= ncos!(2n). 比较系数易得 -16A=1,-6A-8B=0 解得 于是原差分方程的通解为 从所举实例可以看出,差分方程中利用拟初等函数能够为计算带来方便.特别是当m≥2时,使用阶乘幂来确定非齐次线性差分方程的特解,计算过程简单且结果直观明确.


2 常系数非齐次线性差分方程



3 典型实例


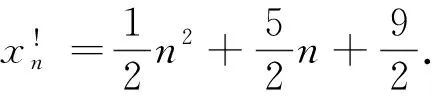
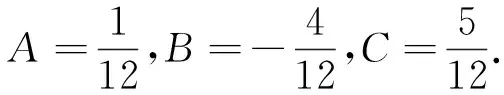
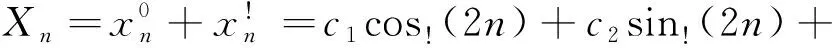
4 结束语

