城际动车组铝合金制动盘热应力场仿真分析

（五邑大学 轨道交通学院，广东 江门 529020）

制动盘作为基础制动装置的核心部件之一，在动车组制动过程中，除了承受来自制动闸片的压力和摩擦力外，还承受摩擦产生的热应力. 制动盘上的温度和热应力分布对制动盘寿命和制动性能有着极其重要的影响[1]. 以密度小、导热性好的铝合金制动盘代替传统铸铁和铸钢材料的制动盘，可降低簧下质量；铝合金良好的导热性更能适应城际动车组频繁制动所带来的制动热负荷变化[2].目前，针对制动盘瞬态温度场的仿真计算较少采用直接耦合的方法，而多采用间接耦合的方法，即先算温度场再将温度结果作为载荷进行应力场计算[3-6]. 在计算摩擦表面产生的热流密度时，普遍采用能量折算法[7-10]，而未考虑摩擦生热因接触长度、半径不同而导致的分布差异. 本文采用热-固直接耦合的方法，以某型城际动车组制动盘为研究对象，对铝合金制动轮盘进行了瞬态温度场和热应力场仿真计算，以验证铝基复合材料制动盘的可靠性.

1 制动盘有限元模型

按照盘的安装位置，动车组制动盘可分为轴盘式和轮盘式[11]，本文选取含有散热加强筋结构的制动轮盘建立单侧盘实体模型. 根据仿真需要，对模型进行简化操作，即一些倒角、小圆角之类的细节结构不予考虑. 本研究中，制动盘的轮对滚动半径为860 mm，制动盘外径640 mm、内径250 mm、厚度18 mm，制动盘摩擦环外径610 mm、内径370 mm，平均摩擦半径245 mm，闸片压力22 kN. 制动盘材料参数如表1所示.

表1 制动盘的材料参数

选取六面体二十节点的实体单元solid226进行离散，该单元能够实现本文所需的结构-热耦合仿真分析. 离散前后模型如图1所示.

图1 制动轮盘几何模型（左）与有限元模型（右）

2 制动盘热模型边界条件

在制动过程中，制动盘和闸片摩擦产生热能，其间的热量传递方式有：热传导、热对流、热辐射，这3种形式在制动过程中同时发生，不过相对于热的传导与对流，辐射所散发的热量非常小，因此本文分析中忽略了这个影响因素.

2.1 热流密度

本文采用摩擦功率法计算热流密度，选取闸片上的一段微分弧块Sdr，该弧块与制动盘圆心之间的距离为r，以Sdr为研究对象，得到作用在这段弧块上的摩擦力FdS：

其中，α是这段弧块的弧度；μ是摩擦系数；P是闸片压强，Pa；FN是闸片压力，N；Sp是闸片摩擦面积，2m. 则弧块Sdr上摩擦力在单位时间内所做的功PdS为：

其中，R是车轮半径，m；vt是列车运行速度，m/s.

假设制动过程中摩擦所产生的热量在周向上是均匀分布的，而且热源是跟着闸片产生的，制动盘在转动，闸片不动，就是说这个热源相对于制动盘来说也是运动的，因此施加在制动盘上面的热流密度应该是总热量与单位面积的比值，而这段弧块所扫过的面积是S= 2 πrdr. 于是作用在这个制动盘的摩擦环当中径向位置r上的热流密度q(t,r)[12]为：

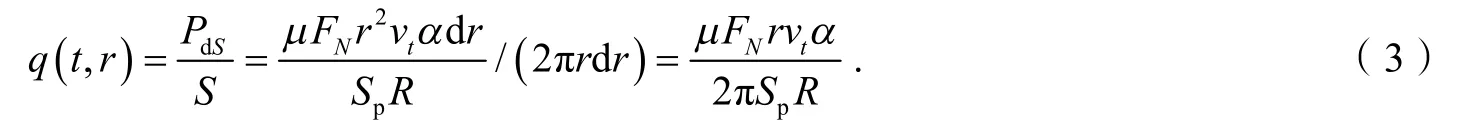
由文献[13]得热流分配系数：

其中，q(t,r)是热流密度，ρ是密度，C是比热容，λ是传热系数；下标d代表制动盘，p代表闸片.

总的热流密度在制动盘和闸片间分配，制动盘上的热流密度为：

综合前文中已知的数据，可以求得本文制动轮盘热流密度的计算公式：

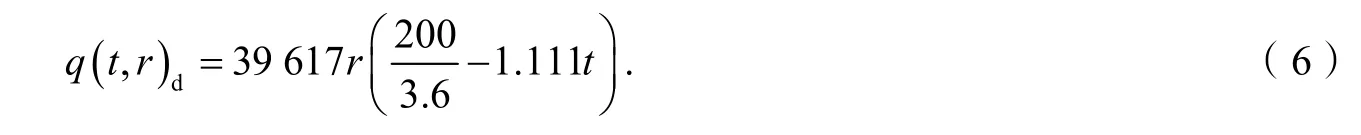
2.2 对流换热系数

对流换热系数与制动盘的外貌形状以及所处空气的流速有关. 制动盘的对流换热系数也是一个变化的值，不同的部位有不同的值，而且系数还会随着时间的变化而变化. 由文献[14]得制动盘与其周围空气之间的平均对流换热系数方程：

其中，Pr是普兰特准数，为 0.703；ν是空气的运动粘度系数，为 1 4.8× 1 0-6m2/s；λ是空气的导热系数，为 2 .59× 10-2W（/m · K）；t是时间；r是制动盘的径向尺寸.

2.3 约束方式

制动过程中，制动盘和闸片摩擦所产生的热效应以热流密度的形式施加在制动盘摩擦表面，制动盘与周围空气之间的对流换热施加在制动盘的各边界表面. 热流密度和对流换热均有两个变化参数，在ANSYS里面采用二维函数来实现.

在 ANSYS中，热流密度和对流换热系数不能同时施加于同一表面，故本文将热流密度加载到制动盘实体表面单元，将对流换热系数加载到制动盘摩擦面的表面效应单元. 因轮盘固定在轮上并且跟随着轮对进行旋转，故对制动盘内圈采取了x轴、y轴和z轴三个轴向上的平移约束.

本研究的城际动车组的制动初始速度为200 km/h，车轮半径为430 mm，该动车组的紧急制动加速度大小为 1 .12 m/s2，理论设计中其紧急工况下的制动距离小于等于1 400 m，则实际制动时间：

3 仿真结果分析

3.1 温度场仿真结果分析

初速度200 km/h的紧急制动工况下，铝合金制动盘三维瞬态温度场仿真计算结果如下：制动盘最高温度发生在制动后43 s，最大值为244.071℃；制动结束之前温度已达到最高，80 s时制动盘最高温度降到150.84℃. 图2为第10 s、43 s、80 s的制动盘温度场云图.

图2 关键时刻制动盘温度场云图

从图2可知：整个制动过程中，制动盘表面温度呈环状分布，最高温度发生在摩擦半径处. 温度场在摩擦环当中呈径向分布，温度梯度较明显，越靠近内圈的节点其温度越低，并且明显能看到热流载荷在周向的这个方向上分布十分均匀.

表2 采样点位置

在制动盘表面、散热筋处和制动盘内部取不同的采样点，提取不同节点的温度变化曲线. 在制动盘模型表面上沿径向取 2组节点，每组按相同间隔取 4个节点，且在制动盘筋板上下都取相应节点，各点位置如表2所示，各点温度的时间历程曲线如图3所示.

图3 制动盘表面不同半径节点制动过程的温度变化曲线

从图3可以看出：随着制动过程的进行，制动盘表面各点的温度都经历了先升高后降低的过程，半径大的节点处于制动摩擦环处，制动热量输入大，且半径越大的节点其最高温度越高；半径较大的节点出现转折的时间较早，半径较小的节点温度变化较平缓.

沿制动盘厚度方向取 2组节点，这两组节点半径不同，每组内各节点间隔为10 mm，具体位置见表3. 各点温度的时间历程曲线如图4所示.

表3 每条曲线所取的节点位置

图4 制动盘不同厚度的节点制动过程温度变化曲线

由图4可知：由于制动盘和制动闸片的摩擦作用，制动盘表面温度最高；随着制动过程的进行，温度由外向内逐渐传递，故沿着厚度方向温度由表面向内依次降低；制动结束后，制动盘表面由于散热条件较好，温度下降快，而盘体内部温度变化缓慢.

3.2 热应力场仿真结果分析

采用直接耦合的方式，可以省去单元转换，直接得到应力场仿真结果. 图5为第10 s、50 s、65 s的制动盘表面应力场云图，制动盘最大应力是243 MPa，出现在第65 s. 制动盘的应力分布趋势呈规律变化，应力在制动盘上呈环状分布，最大等效应力出现在制动盘表面及散热筋板处. 这是因为制动过程中，制动盘摩擦面和制动闸片一直处于摩擦状态，产生的大量热量传递需要一定时间，所以，制动盘最大应力在制动盘表面及散热筋板处.

图5 关键时刻点的应力场云图

按表2在制动盘模型表面上沿径向取2组节点，每组按相同间隔取4个节点，且在制动盘筋板上下都取相应节点，各点热应力的时间历程曲线如图6所示.

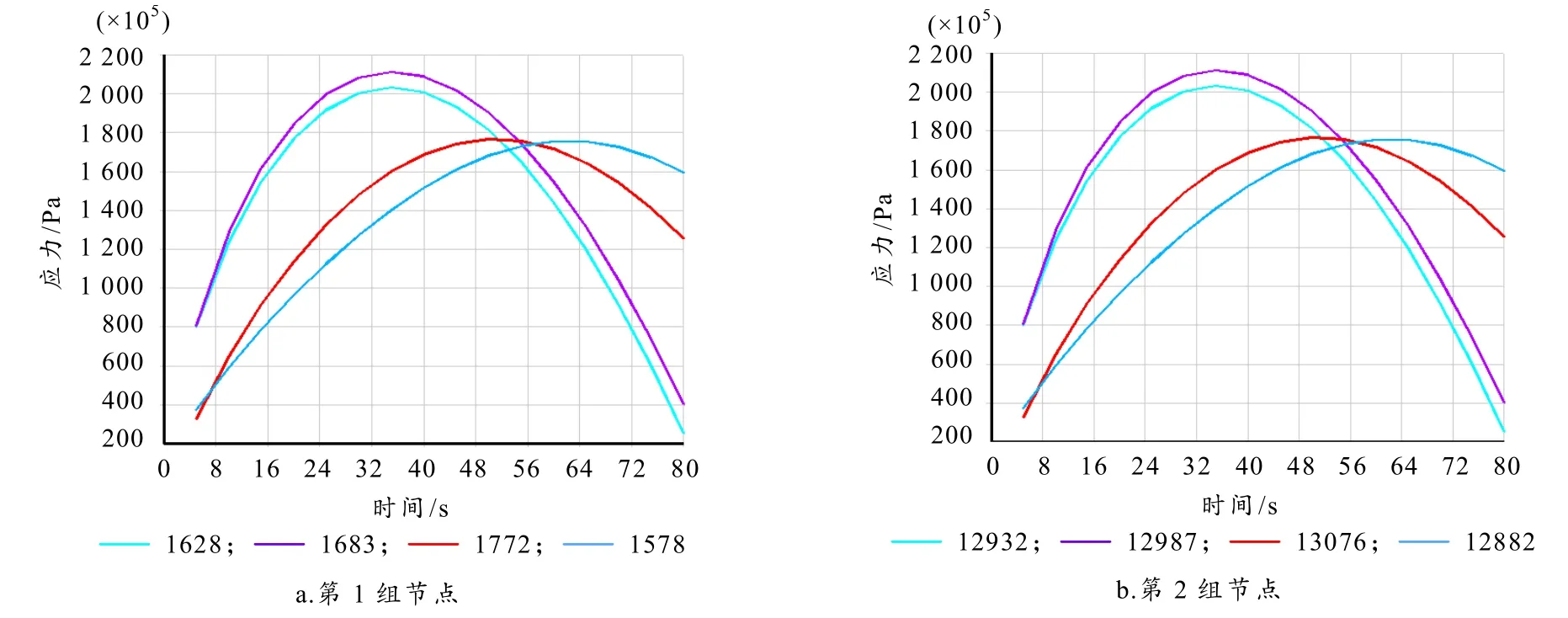
图6 制动盘表面不同半径节点制动过程的热应力变化曲线

由图6可知：随着制动过程的进行，制动盘表面各点的应力经历了先升高后降低的过程，变化趋势与相应各点温度变化趋势一致；制动盘应力最大位置为制动盘摩擦环处，且存在从摩擦环中心向内外两侧逐渐递减的趋势.

同表3，沿制动盘厚度方向取两组节点，两组节点半径不同，每组内各节点间隔为10 mm. 各点热应力的时间历程曲线如图7所示.

图7 制动盘不同厚度的节点制动过程热应力变化曲线

由图7可知：由于制动盘和制动闸片的摩擦作用，制动盘表面温度最高；随着制动过程的进行，温度由外向内逐渐传递，温度的传递直接影响着制动盘的热应力，所以沿着厚度方向热应力由表面向内依次降低；半径相同处的各节点，热应力变化趋势一致，且最大热应力出现时间逐渐延后.

4 结论

通过对制动盘制动过程进行仿真，得到城际动车组铝合金制动轮盘的温度和热应力分布规律.从制动盘温度场仿真结果看，制动结束后30 s左右，制动盘表面及内部温度降至外温. 热应力仿真结果表明，制动盘最大热应力为243 MPa，未达到材料屈服应力. 由此可知：铝合金材料制动轮盘能满足200 km/h城际动车组频繁起停对制动盘的要求. 上述结论可为铝合金制动轮盘的结构设计、材料选择等提供参考依据. 本文针对轮盘制动盘温度场和热应力进行了仿真研究，而制动轴盘制动过程中的热性能有待继续深入研究.