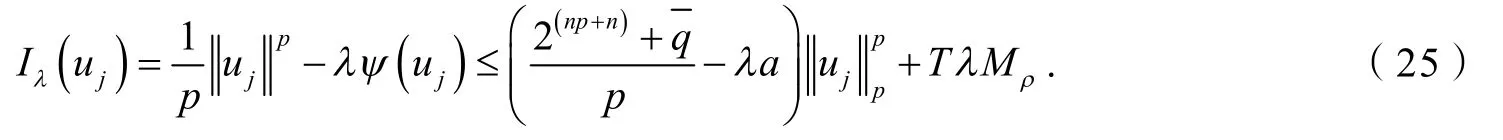具有p-Laplacian算子的高阶差分方程的周期解
旷菊红,石艳香,袁利国
(1.五邑大学 数学与计算科学学院,广东 江门 529020;2.山西大学 数学科学学院,山西 太原 030006;3.华南农业大学 数学与信息学院数学系,广东 广州 510642;4.玉林师范学院 复杂系统优化与大数据处理广西高校重点实验室,广西 玉林 537000)
1 引言与主要结果
本文主要研究一类具有p-Laplacian算子的高阶差分方程
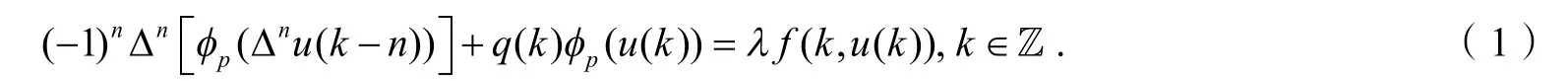
的周期解,这里n为确定的正整数,p为大于1的常数,对所有的是一个正的T周期序列,这里T是一个正整数.f:Z×R→R,对第一变量是T周期的,对第二变量连续的.Δ是差分算子:
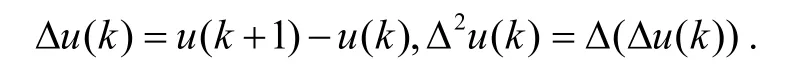
差分方程出现在很多领域[1-2],比如经济学、计算机科学等. 近十年来,离散p-Laplacian问题已经成为热点问题[3-12],其中采用的方法有上下解的方法、不动点理论、山路引理和环绕定理等. 最近临界点理论有一些新的研究成果[7,13-19],其中G.Bonanno[13]在研究变分泛函为无下界的情形时,得到最少存在两个不同的临界点.
Deng[8]研究了非线性项f在无穷远点和零点都是超p次时,式(1)周期解的存在性,我们[12]用山路引理结合周期逼近也研究了非线性项f在无穷远点和零点都是超p次时,式(1)同宿解的存在性. 然而,当非线性项f在零点处是次p次时,山路引理不能直接使用,受文献[5]、[7]和[12]的启发,本文要研究当非线性项在零点处是p次时,式(1)的周期解问题.
在本文中,我们假设以下两个条件总是满足:
(q)q(k)>0且对所有的k∈ℤ ,q(k+T)=q(k).和q*分别表示{q(k)}的最大值和最小值.
(f)f(k,u)关于第一变量是T周期的,关于第二个变量连续的,且.
下面首先介绍本文的主要结果.
定理1假设条件(q)和(f)成立,且对所有的x<0 ,k∈[1,T]都有f(k,u)≥ 0 ,
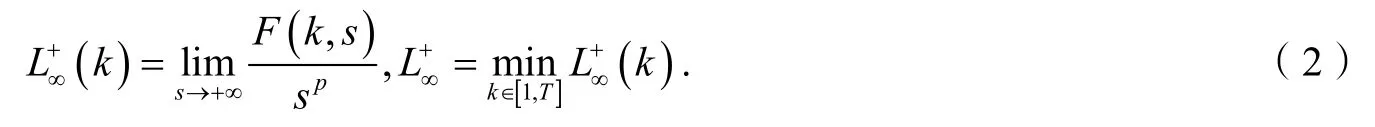
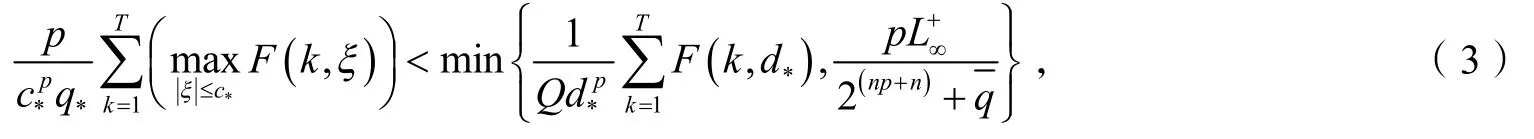
其中
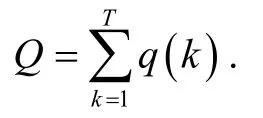
则对每一个λ∈Λ1,
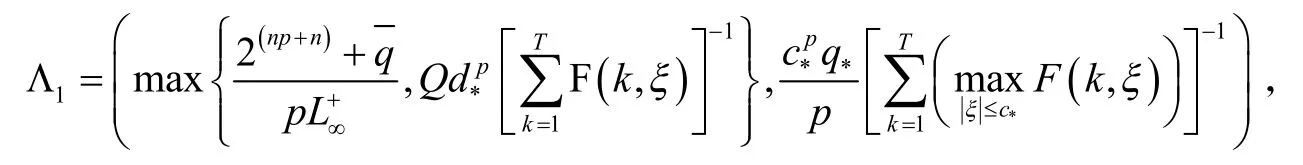
式(1)至少存在两个非零周期解uλ1和uλ2.
推论 1假设条件(q)和(f)成立,且对所有的x<0 ,k∈[1,T]都有f(k,u)≥ 0 ,如果对所有的k∈[1 ,T],
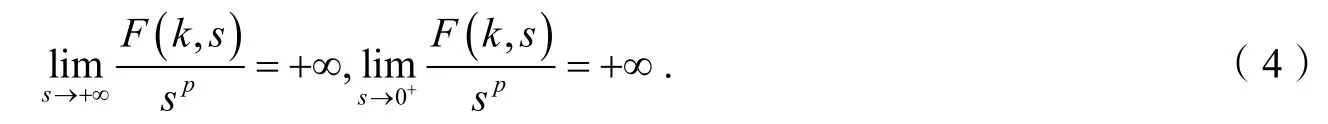
则对每一个λ∈Λ*,
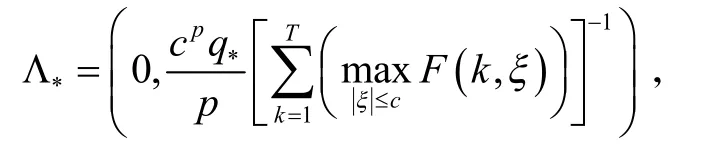
这里c为任意正数,式(1)至少存在两个非零周期解.
例1取p= 2 ,n= 1 ,T= 2 ,对所有的k∈[1,T],都有q(k)=1和
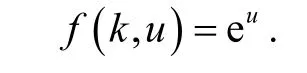
定理2假设条件(q)和(f)成立,如果存在两个正常数a和ρ,使得
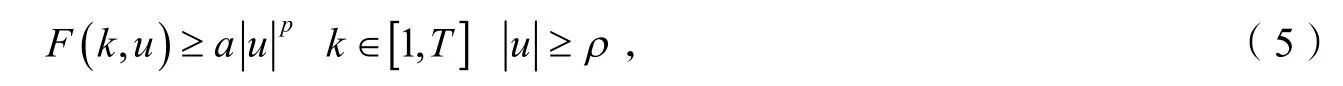
而且存在两个正常数c*,d*,并满足d*<c*和
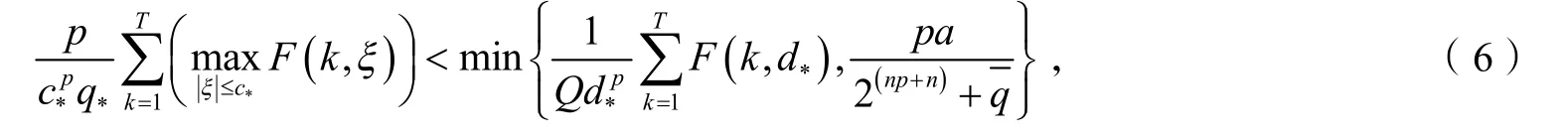
其中
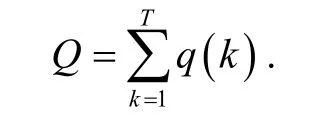
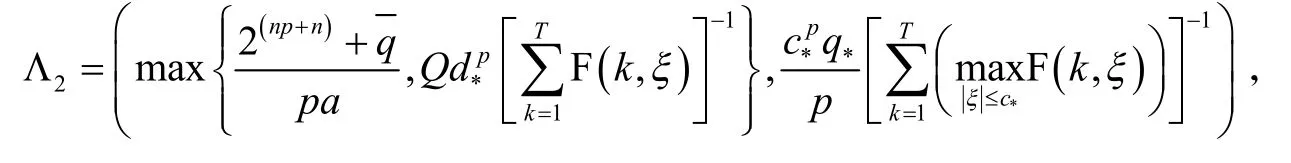
式(2)至少存在两个非零周期解uλ1和uλ2.
注1假设定理2所有的条件满足,而且对任意的k∈ℤ,f(k,u)关于u是奇函数,则式(1)至少存在四个非零周期解±uλ1和±uλ2.
推论2假设条件(q)和(f)成立,对任意的k∈ℤ ,f(k,u)关于u是奇函数,且对任意的k∈[1,T],有
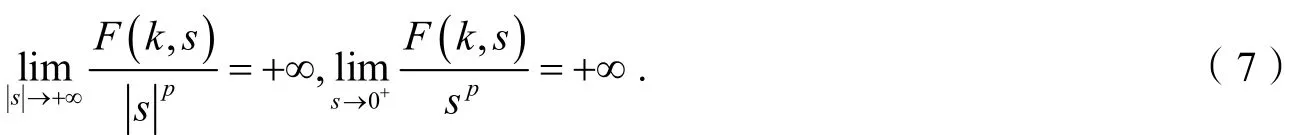
则对每一个λ∈Λ*,
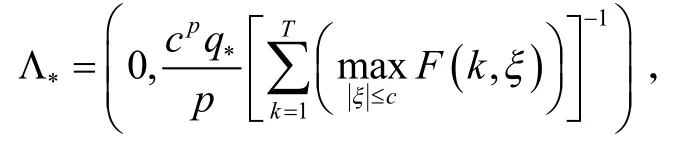
这里c为任意正数,式(1)至少存在四个非零周期解.
例2取p=2 ,n=1 ,T= 2,对所有的k∈[1,T],都有和
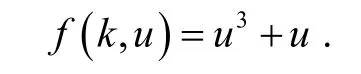
容易证明,对任意的λ∈(0,13),推论2的所有条件都满足,所以式(1)至少存在四个非零周期解.
2 变分框架
本节我们将建立与方程式(1)相应的变分框架,并给出证明主要结论所需的引理.令
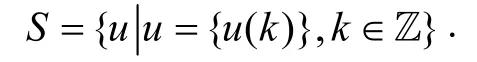
定义S的子集E为
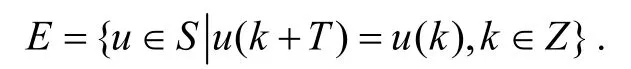
显然E是S的一个线性子空间,与RT同构. 在E中定义范数如下:
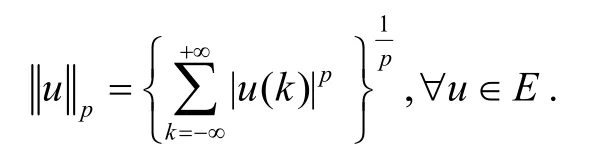
在E上定义泛函
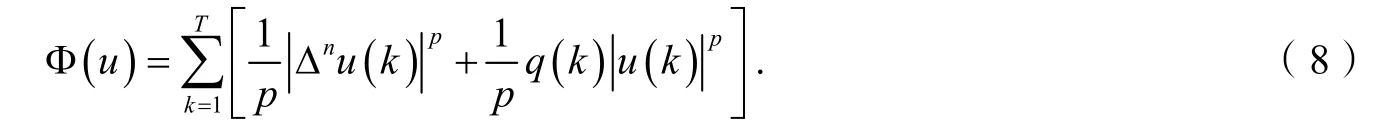
由于
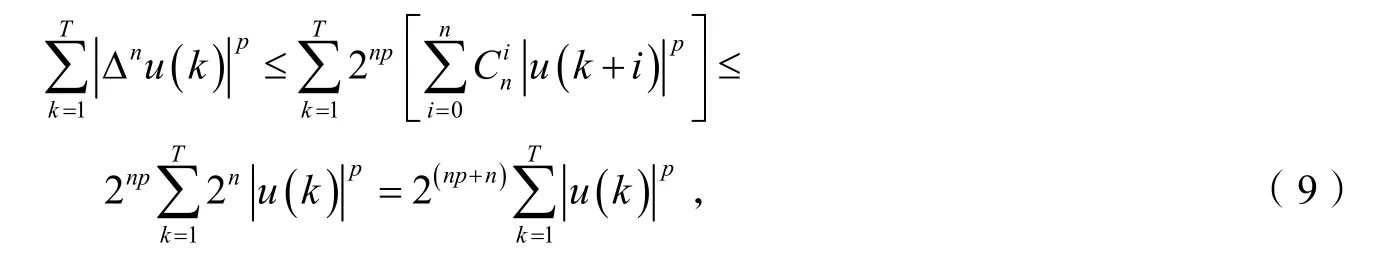
所以
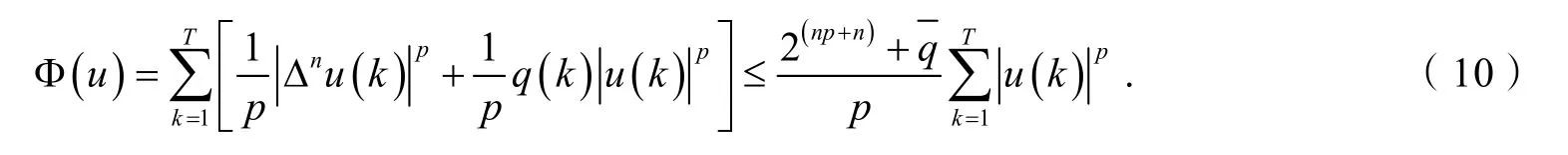
在E上我们又定义范数如下:
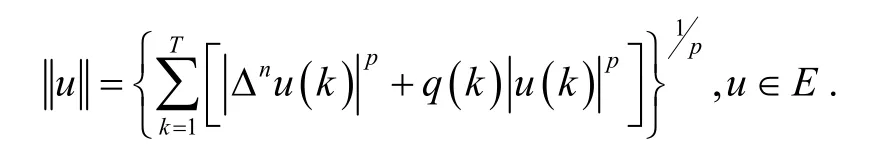
又定义泛函ψ(u),
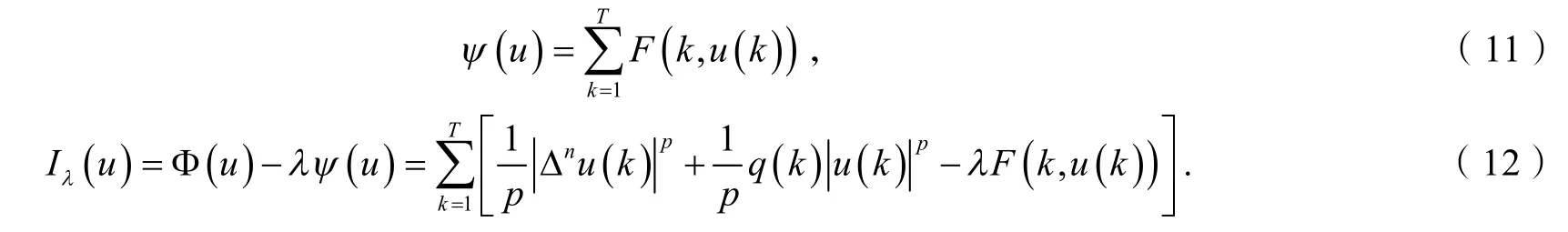
容易证明 Φ,ψ∈C1(E,R),且Frechet导数为
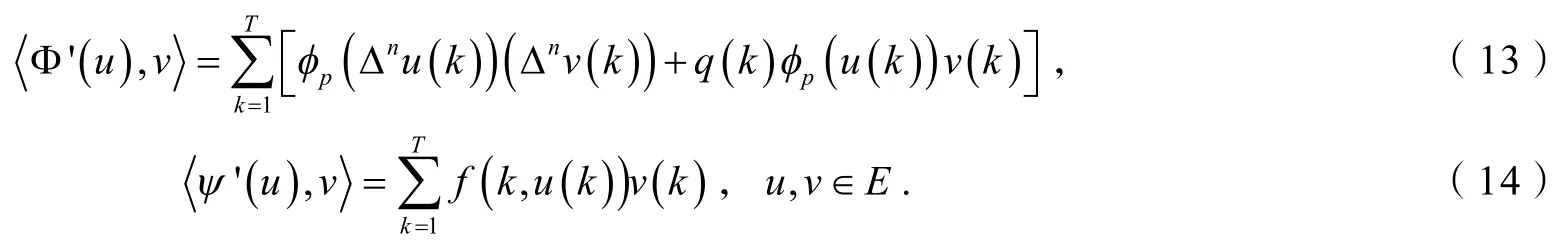
由于
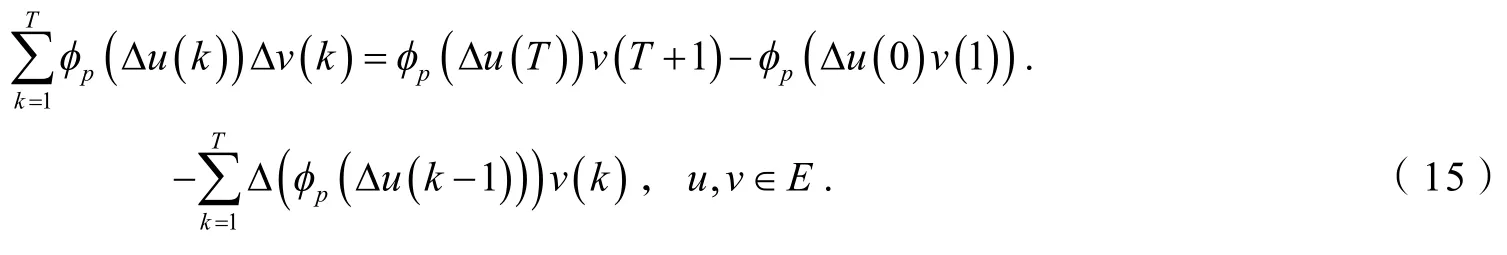
所以
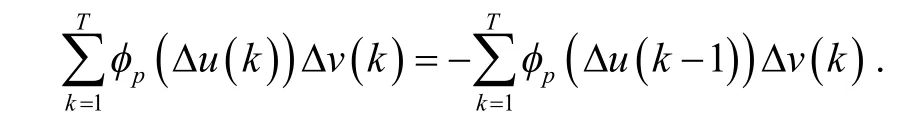
且
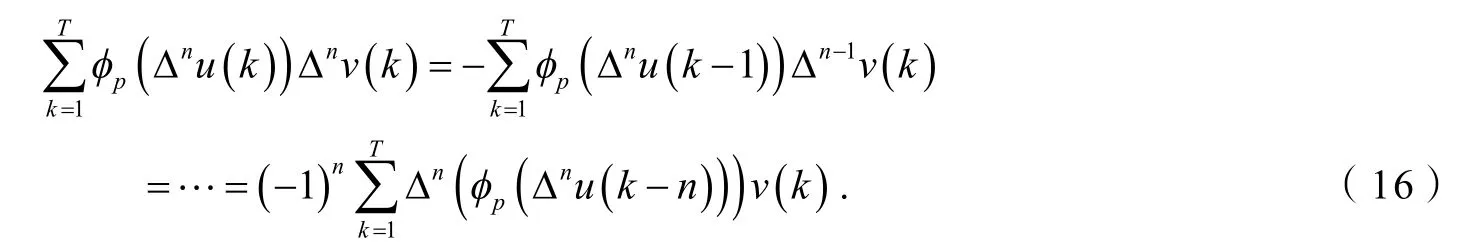
由(13)、(14)和(16)可知,Iλ在E上的临界点是式(1)的周期解.
定义1假设是一个序列,如果是有界的且随着j→+∞,我们称{xj}是I的Palais-Samale序列(P.S序列). 如果I的任意一个P.S序列都有一个收敛的子列,我们称I满足P.S条件.
为证明主要结论,我们需要下面的引理.
引理1[4]X是实Banach空间,且 Φ,ψ∈C1(X,R),均满足. 假设存在r∈R,u*∈X,使得0<Φ(u*)<r和

且对任意的
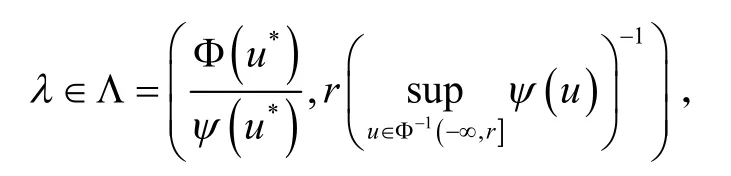
泛函Iλ=Φ-λψ满足P.S条件且是无下界的. 则对每一个Iλ至少存在两个非零的临界点uλ1和uλ2,且满足Iλ(uλ1)<Iλ(uλ2).
3 主要结果的证明
引理2假设,且对所有的x<0 ,k∈[1,T],都有f(k,x)≥ 0 ,则对任泛函Iλ满足P.S条件且是无下界的.
引理2的证明假设序列是E中的一个序列,且满足随着j→+∞. 对任意的k∈ℤ,定义},则,,且对任意的.
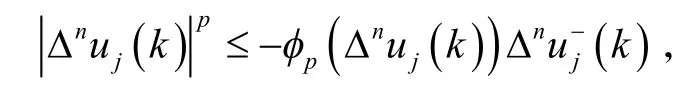
且
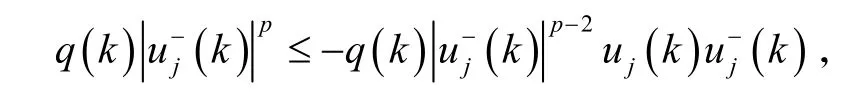
所以
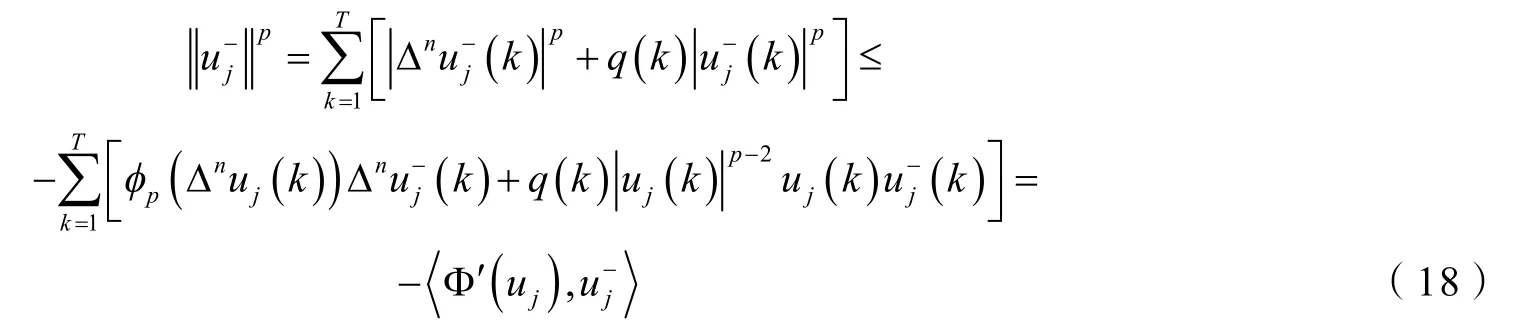
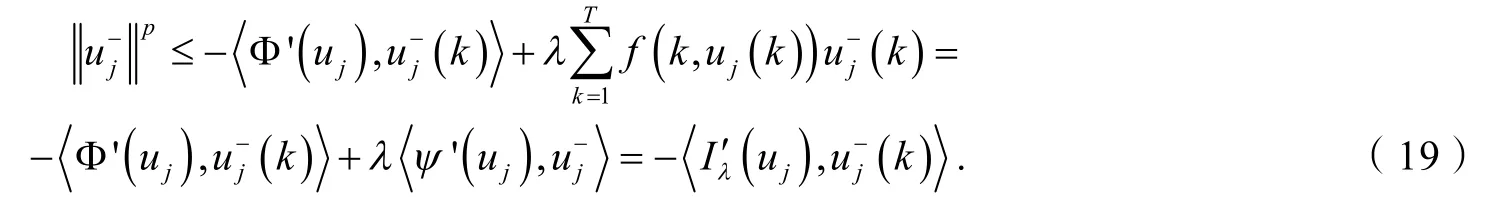
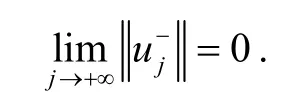
由上式可知,存在正常数M>0使得对所有的k∈[1,T] ,j∈ℤ+,都有,所以,即

然后,我们证明{uj}是有界的. 用反证法,假设{uj}是无界的,也就是是无界的,由可得,存在正常数δ>0,使得对所有的s>δ和k∈[1,T],都有F(k,s)>lsp. 定义
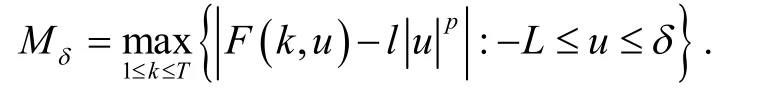
再由F(k,u)的周期性和式(20),容易证明
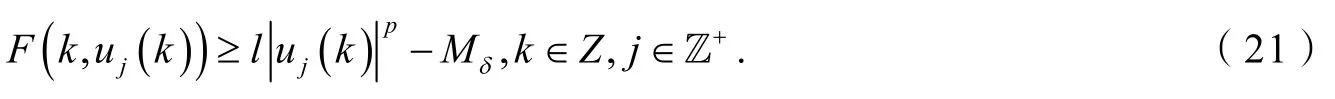
因此,对任意的j∈ℤ+,
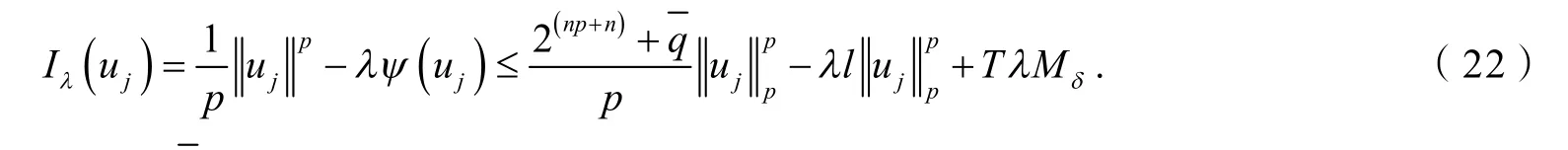
定理1的证明因为Φ和ψ分别如式(8)和(11)所定义,易证Φ和ψ满足引理1的所有假设,为了应用引理1,下面只需证明式(17)即可.
任取u∈Φ-1(-∞,r],则
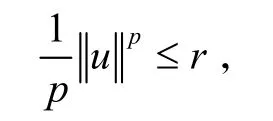
则
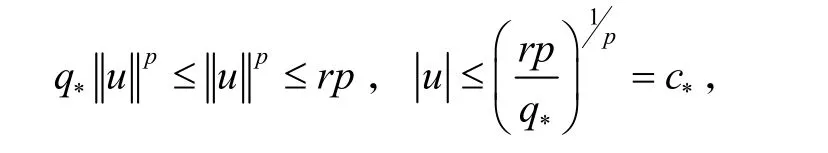
且
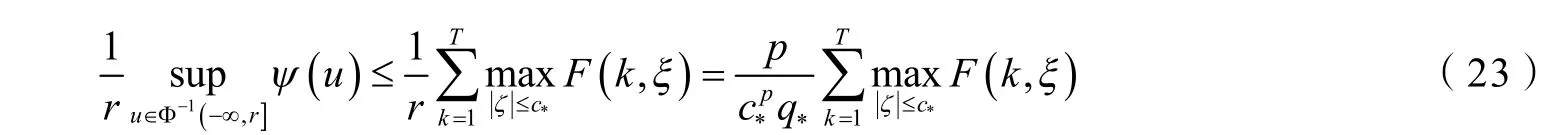
这里
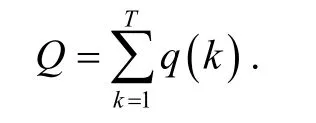
则易证 Φ (u*)<r且
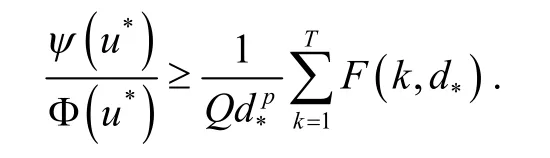
再由式(23)和(3),可得式(17). 所以由引理1得,对任意的λ∈Λ1,方程(1)至少有两个非零的解. 证毕.
定理2的证明首先证明,对任意的,泛函Iλ满足 P.S条件且是无下界的.
假设序列{uj}是E中的一个序列,且{Iλ(uj)}是有界的,即存在M*使得
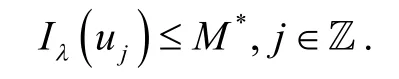
定义
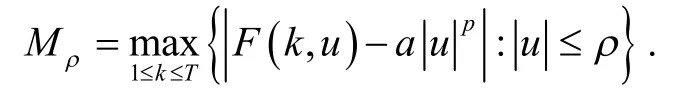
易证,
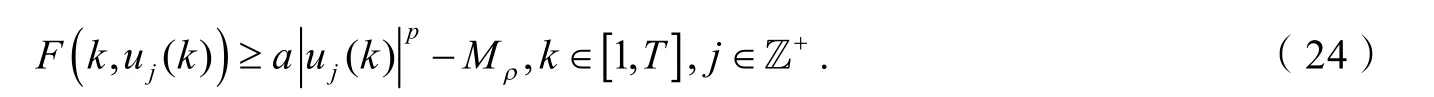
结合式(9)可得,对任意的j∈ℤ+