Y-Gorenstein模类导出的对偶对

（陇南师范高等专科学校 数信学院，甘肃 陇南 742500）

1 预备知识

1995年，Enochs[1]介绍了 Gorenstein内射模的概念，它与 Gorenstein投射模、Gorenstein平坦模是Gorenstein同调理论的重要研究对象. 孟凡云等[2]提出了X-Gorenstein投射模、Y-Gorenstein内射模和Y-Gorenstein平坦模的概念，并证明当rY-GID（R）＜∞时，(⊥YGI,YGI)是一个完全的遗传余挠理论. 当R为右凝聚环且 l Y-GFD（R）时，(YGF,YGF⊥)是一个完全遗传余挠理论. 2017年，Alacob[3]讨论了双边Nother环上Gorenstein内射模的包络与覆盖. 本文将利用Y-Gorenstein包络与覆盖等工具进一步研究由Y-Gorenstein模类导出的对偶对(⊥YGI,YGF⊥)及(YGI,YGF).

本文中的环R均指有单位元的结合环，模指酉模.M+= H omZ(M,QZ)表示R模M的示性模. Y表示包含所有内射模的右R模类. 先介绍一些涉及到的概念.

称右R模M是Y-Gorenstein 内射模[2]539，如果存在正合列

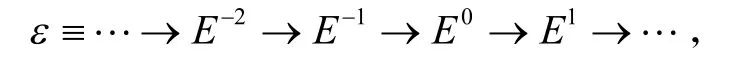
其中，Ei为内射模，M= K er(E0→E1)且对任意H∈Y有正合列ε在函子HomR(H,-)仍正合. 用YGI表示所有Y-Gorenstein 内射模组成的类.

称左R模M是Y-Gorenstein 平坦模[2]550，如果存在正合列

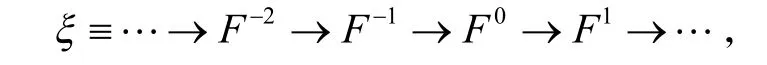
其中，Fi为平坦模，M= K er(E0→E1)且对任意G∈Y有正合列ξ在函子G⊗-仍正合. 用YGF表示所有Y-Gorenstein平坦模组成的类.

注：1）内射模⇒Y-Gorenstein内射模⇒Gorenstein内射模;

2）平坦模⇒Y-Gorenstein平坦模⇒Gorenstein平坦模.

为了方便讨论，我们用Y-GiD(M)表示R模M的Y-Gorenstein内射维数，Y-GfD(M)表示R模M的 Y-Gorenstein平坦维数. 记是 任意右R模}，l Y-GFD （R）=sup{Y-是左R模} . 设F为R模类，F的右正交类记为对任意F∈F都有.对偶地，F的左正交类记为.

称(L,C)是一个余挠理论[4]，如果L⊥=C，且⊥C=L. 称余挠理论(L,C)是完全的，如果对任意右R模M都存在正合列0 →C→L→M→0和0 →M→C′→L′→0，其中C,C′∈C，L,L′∈L. 称余挠理论(L,C)是遗传的，如果以下等价条件之一成立：

1）L关于满同态的核封闭；

2）C关于单同态的余核封闭；

3）对任意i≥1，任意C∈C,F∈L有.

本文涉及到的概念和记号参见文献[5-6].

定义1[7]623设M为R模类，C为Rop模类. 称(M,C)为对偶对，如果满足

1）对任意R模M，有M∈M ⇔M+∈C；

2）C关于直和因子及有限直和封闭.

引理1[2]547设rY-GID（R）＜∞，则(⊥YGI,YGI)是一个完全遗传余挠理论.

引理2[2]551设M为左R模，则以下条件等价：

1）M是Y-Gorenstein平坦左R模；

2）M+是Y-Gorenstein内射右R模.

2 主要结论

命题1如果M∈Y GF∩ Y GF⊥，那么M是平坦模.

证明由M∈YGF 知，存在正合列0 →M→F→G→ 0 ，其中F是平坦模，G是 Y-Gorenstein平坦模. 用函子HomR(-,M)作用于上正合列得

因为M∈YGF⊥而G∈Y GF ，所以. 可见短正合列0 →M→F→G→ 0 可裂，从而M是平坦模F的直和因子. 因此M是平坦模.

命题2设rY-GID（R）＜∞，且对任意M∈Y GI 有M+∈Y GF . 则有

证明（充分性）设K∈⊥YGI ，由引理2知Y-Gorenstein平坦模的示性模是Y-Gorenstein内射模，即对任意B∈Y GF 有B+∈Y GI . 从而. 而可见，因此K+∈Y GF⊥.

（必要性）设K+∈Y GF⊥. 由于rY-GID（R）＜∞ ，由引理 1知存在正合列0 →K→C→L→0，其中C∈Y GI ，L∈⊥YGI . 从而有正合列0 →L+→C+→K+→ 0 . 根据引理2可知L+∈Y GF⊥，可见C+∈Y GF⊥. 因此C+∈Y GI∩ Y GF⊥. 由命题1知C+是平坦模，又由文献[4]中定理3.2.16知C是内射模.注意到内射模一定是 Y-Gorenstein内射模，所以在正合列0 →K→C→L→0中C∈⊥YGI ，L∈⊥YGI . 由于(⊥YGI,YGI)是一个完全遗传余挠理论，所以K∈⊥YGI .

定理1设rY-GID（R）＜∞且对任意M∈Y GI 有M+∈Y GF ，则(⊥YGI,YGF⊥)是一个对偶对.

证明根据假设条件及命题 2可知K∈⊥YGI ⇔K+∈Y GF⊥. 因为YGF⊥关于直积、有限直和、直和因子封闭，由定义1得(⊥YGI,YGF⊥)是一个对偶对.

引理3[2]553设R为右凝聚环且 l Y-GFD（R）＜∞时，(YGF,YGF⊥)是一个完全遗传余挠理论.

有了以上结论，可得如下定理.

定理2设R为右凝聚环且rY-GID（R）与 l Y-GFD（R）均有限，且对任意M∈Y GI 有M+∈Y GI .则(YGI,YGF)是一个对偶对.

证明先证对任意R模K有K∈YGI ⇔K+∈YGI .

(⇐ 设K+∈Y GF ，由引理1知存在正合列0 →K→C→L→ 0 ，其中C∈Y GI ，L∈⊥YGI . 由引理2及L∈⊥YGI 得L+∈Y GF⊥，考虑正合列0 →L+→C+→K+→ 0 ，用函子作用于该正合列得因为K+∈Y GF ，所以. 可见短正合列0 →L+→C+→K+→ 0 可裂，C+≅L+⊕K+且L+∈Y GF ，因此L+∈Y GI∩ Y GF⊥，由命题1知L+是平坦模，L是内射模. 在正合列0 →K→C→L→0中C∈Y GI 且L是内射模，因此K具有有限 Y-Gorenstein内射维数，根据文献[2]中命题 2.12，存在正合列0→I→F→K→ 0 ，其中C∈Y GI ，F内射维数有限. 因此序列0 →K+→F+→I+→ 0 正合且I+,K+∈Y GF ，从而F+∈Y GF . 由文献[4]中定理3.2.19知F+具有有限平坦维数，又因为具有有限平坦维数的Gorenstein平坦模一定是平坦模，注意到Y-Gorenstein平坦模一定是Gorenstein平坦模，由文献[4]中推论10.3.4可得F+是平坦模. 从而F是内射模. 因此K∈Y GI.

⇒ )由定理条件易证.

因此对任意R模K，有K∈YGI ⇔K+∈YGF .

下证(YGI,YGF)是一个对偶对. 定义1的第一个条件已经成立. 又由文献[2]中命题4.5易知YGF关于有限直和及直和因子封闭. 因此(YGI,YGF)是一个对偶对.