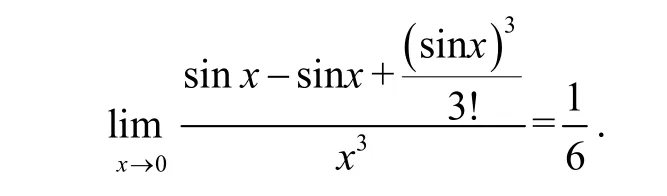等价无穷小代换求极限的讨论
(大连民族大学 计算机科学与工程学院,辽宁 大连 116605)
无穷小有很多的性质,它在数学运算中起了重要作用,其中用等价无穷小代换法求极限是突出的表现[1]. 设α、β为两个无穷小,有如下定理:
定理1[2]设α~α′,β~β′且存在,则.
当α或β为一个和差形式的多项式时,它们的等价无穷小往往不能直接求出,这时可使用等价无穷小代换多项式中各个单项来求极限. 比如求,由sin5x~5x,tan3x~3x,,有

然而此法并非万能,它的使用是有条件的,稍不注意就会计算错误[3],原因是对α、β各个单项用等价无穷小代换后得到的式子与α、β不互为等价无穷小[4]. 比如求,用sinx-sinx替换sinx-tanx,可得. 而sinx-sinx与sinx-tanx不互为等价无穷小,故出错. 然而sinx-sinx与sinx-tanx不互为等价无穷小无法从直观上得出,故很多教科书都存在只能代换极限里分子、分母中的乘积因子,而不能随意代换其中加减法因子的说法[5]. 本文将给出一种和差形式的多项式均可采用等价无穷小量代换其中各个单项的条件[6].
为方便叙述,对下文给出统一记号:令
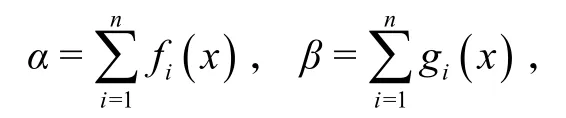
其中,fi(x)、gi(x)为α、β的一个单项式,i∈[1,n].
设α和β被等价无穷小代换后为A和B,当只对α或只对β代换,所得极限为. 又设b为代换前和代换后的差值在α和β同一变化过程中的极限,所以b有两种形式:
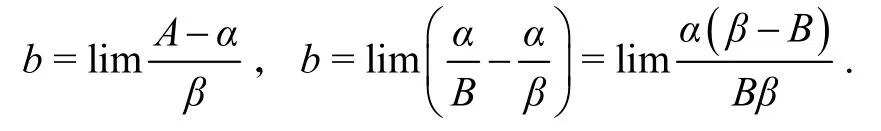
当对α和β同时代换时,可视为先后进行这两种操作.
又 ∀i∈[1,n],有Fi(x)~fi(x)、Gi(x)~gi(x),故有

设fi(x)ri阶可导,x→a,则和差运算中各部分无穷小按泰勒公式展开可得[7]:
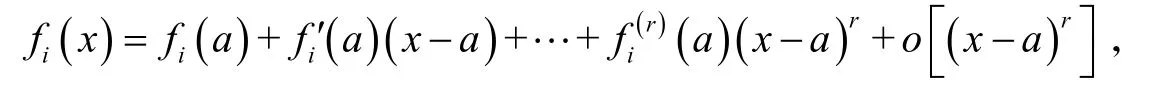
设Fi(x)Ri阶可导,Ri≤ri,所以有

同理,设gi(x)si阶可导,Gi(x)Si阶可导,Si≤si,有
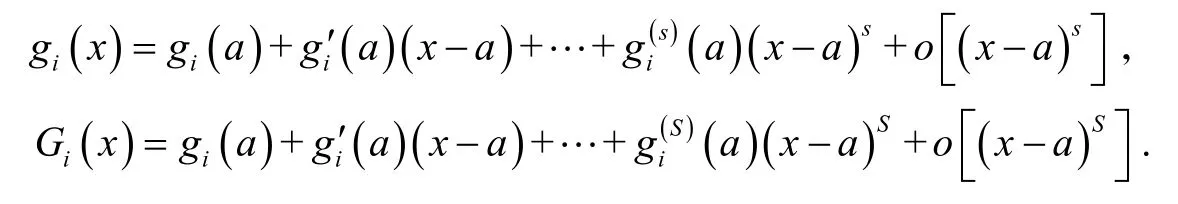
1 使用等价无穷小进行单项代换的条件
以下两个定理是为了保证定理1中α~α′,β~β′成立.
定理2若b=0,则α~A,β~B.
证明若b=0,则. 又limβ=0,所以lim(A-α)=0 ,即A=α,所以A~α.若,则,所以,即B~β.
定理3设,又有R≥t或S≥t,则有b=0.ii
证明i)对于,. 故
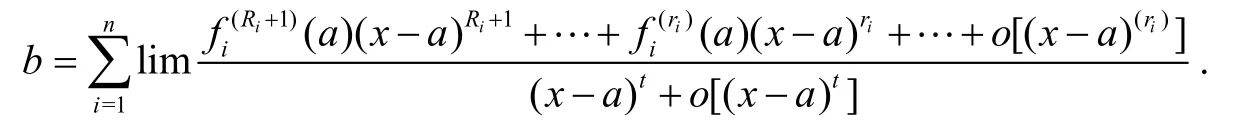
此时只须Ri≥t,就有b=0,否则b≠0.
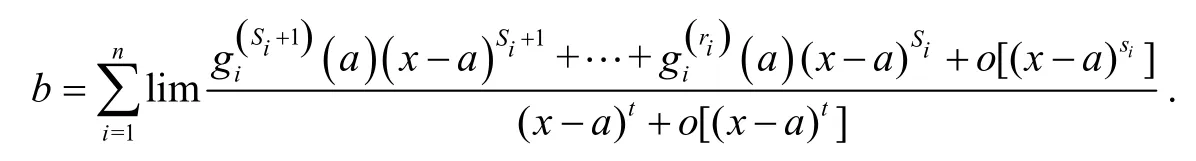
此时只须Si≥t,就有b=0,否则b≠0.
综上,只要满足了定理3,使b=0,也就满足了定理1,就可以进行和差分式上对于单项的等价无穷小替换.
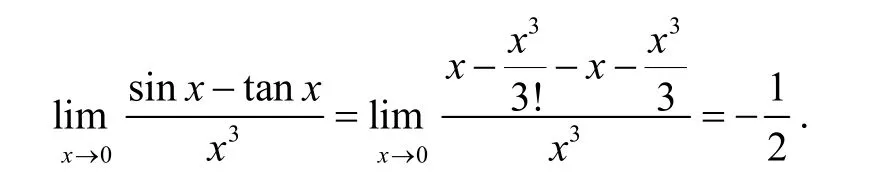
所求极限正确.
2 典型题
例1
解这是的形式,故只对β进行替换. 此时,;使用代换g1(x)和g2(x),则有S1=6,S2=6,且有,此时有

例2
解这是的形式,此时使用代换f1(x)和f2(x),则有R1=3,R2=3,,此时有

例3
解这是的形式,此时,使用代换f2(x),则有此时有

例4
解这是的形式,此时),使用代换f2(x),则有R2=3,R2≥t=3 ,R1=r1=∞>t,此时有