双站时差频差定位技术
刘 苏,马 丹,周智勇
(1.中国洛阳电子装备实验中心,河南 洛阳 471003; 2.上海微波设备研究所,上海 201802;3.中国科学院微电子研究所,北京 100029)
0 引 言
对目标的定位分为有源和无源定位。有源定位主要有雷达、激光、声纳等定位方式,一般是通过发射信号到目标,然后通过检测回波的方式实现定位。有源定位的主要缺点是容易被发现,从而遭受到电子干扰及反辐射导弹等武器攻击。无源定位不发射信号,通过接收辐射源的信号进行定位,因而,无源定位具有隐蔽、不易被发现的优点。
随着科技的进步,现代战场电子战环境也越来越复杂,依靠传统的有源定位已满足不了现代战场环境的需要,因而,迫切需求一种新的定位手段来实现对目标的快速准确定位。无源定位的隐蔽及快速定位的特点受到各国越来越多的重视,它对于保存自己、摧毁敌人都具有非常重要的意义,已成为了电子战的核心技术之一。
无源定位系统利用的是目标辐射源发射信号来进行目标定位。因为接收辐射源信号是单程传输,因而可探测的距离更远,且同时具有很好的隐蔽性与很强的抗干扰能力。此外,无源定位系统不发射信号,不需要大功率的发射机,可以节约成本较高的发射单元,从而提高了经济效率。
对辐射源的无源定位,可以用单平台、双平台、多平台进行,分别称为单站无源定位、双站无源定位和多站无源定位。平台承载的无源传感器(观测器)可以获得无源测量,通常有目标辐射信号的到达角(DOA)、到达时间差(TOA)、频率差(FDOA)等,每个测量值确定一个定位曲面(线),多个曲面(线)相交得到目标的位置,多次测量、定位和滤波得到目标的航迹[1-3]。
只需要使用一个观测平台的单站无源定位进行侦察和对敌方目标定位时,它需要的资源少,成本低,但目前为止,可实现性还比较差,参数的测量精度很难达到实际使用需求。多站无源定位设备由多个探测站构成,需要的资源量大,技术复杂,需要解决不同探测站点之间时间同步问题。因而,采用双平台定位可以将单平台和多平台定位的优缺点进行综合,且双平台实现也相对容易,若运用于运动平台,组队也比较灵活。双站定位由2个空间上分离配置平台上的接收机同时对辐射源信号进行接收处理,确定2个定位曲线或曲面,或2个曲线或曲面相交,得到目标的位置。它主要利用不同平台定位曲面之间差异较大这一特点来定位和提高定位精度,具有速度快、精度高等优点。双平台定位跟踪是靠2个平台之间的协同工作,系统由主站和辅站联合组成。主站和辅站都利用探测设备测定辐射源信号属性参数及到达时刻信息,辅站利用转发器把接收到的辐射源信号转发给主站,主站则采取信号匹配技术从直达信号和转发信号来计算辐射源的位置,从而实现对目标的探测和定位。
1 时差频差定位原理

Δt=(r2-r1)/c
(1)
(2)
(3)
(4)

(5)

(6)
式中:r1,r2分别为辐射源至接收站1和接收站2的距离;c和f0分别为光速和接收信号的频率;vr1/r1,vr2/r2分别为辐射源与载机1和载机2的径向相对速度。
辐射源的高度通常可以通过先验知识进行估计,因而,不考虑俯仰维的情况下,时差频差方程可简化为:
(7)
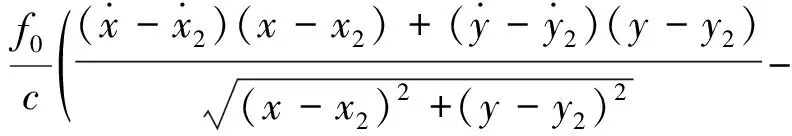
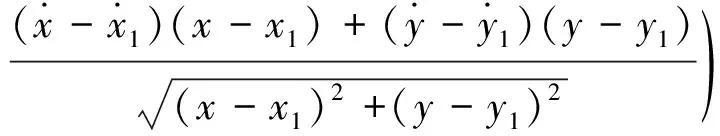
(8)
通过联立时差频差方程可求出辐射源的坐标和速度。当目标为固定辐射源时,方程简化为:
(9)
(10)
2个方程,2个未知数,因而通过1次观测即可得到辐射源的位置。对于运动目标,理论上需要至少2次观测可以得到辐射源的前后位置和速度。
2 双站时差频差定位误差分析
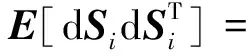
对TDOA-FDOA方程式(1)和(2)进行全微分,整理得定位误差协方差阵为[4-5]:

(11)
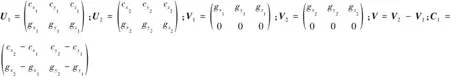
对辐射源的定位误差为:
(12)

3 航迹滤波
这一节介绍时差频差定位的航迹滤波方法,包括基于扩展卡尔曼滤波(EKF)和无迹卡尔曼滤波(UKF)的方法。
3.1 EKF
目标的状态方程为:
x(k+1)=F·x(k)+n(k)
(13)


目标状态预测值表示为:
x(k|k-1)=F·x(k-1|k-1)
(14)
式中:x(k-1|k-1)为k-1时刻的状态值;x(0|0)=x(0)为目标的初始状态值;x(k|k-1)为k-1时刻的预测值。
预测协方差矩阵表示为:
P(k|k-1)=F·P(k-1|k-1)FT+Q(k)
(15)
式中:P(k-1|k-1)表示k-1时刻的状态协方差;P(0|0)=P(0),表示状态协方差初始值。
卡尔曼增益矩阵表示为[6]:
K(k)=P(k|k-1)H(k)T[H(k)·
P(k|k-1)×H(k)T+R]-1
(16)
式中:H(k)为时差频差的雅克比矩阵;R为测量误差协方差矩阵。
雅克比矩阵为:
(17)


(18)
目标状态的更新方程为:
x(k|k)=x(k|k-1)+K(k)·
[z(k)-z(k|k-1)]
(19)
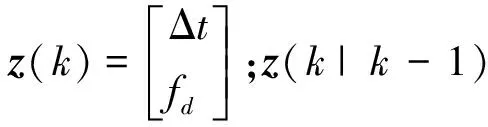
目标状态协方差更新为:
P(k|k)=[I-K(k)·H]·P(k|k-1)
(20)
式中:I为单位矩阵。
3.2 UKF
无损变换(UT)变换是一种计算随机变量经过非线性变换之后的统计特性的方法。设随机变量的均值和方差分别为x和P,根据均值和协方差产生样本点和加权系数,则:
(21)
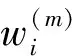
计算k时刻的预测均值、预测协方差和样本点[7]:
χi,k|k-1=f(χi,k-1)=F·χi,k-1,i=0,1,…,2L
(22)
(23)
(24)
(25)
样本点经过非线性变换后的均值和协方差为:
(26)
(27)
(28)
对状态估计进行更新:
(29)
(30)
(31)
(32)
4 定位误差与航迹跟踪仿真
下面给出时差频差定位误差仿真结果。图1(a)中时差精度10 ns, 频差精度10 Hz,基线距离40 km,速度误差0.5 m/s,位置误差10 m,辐射源频率为9 GHz,接收站1速度v1=[300, 0, 0] m/s,接收站2速度v2=[300, 0, 0] m/s,定位目标速度v=[0, 0, 0] m/s。基线法线方向300 km处的定位误差约5 km,可达2%R的定位精度。当基线扩大到100 km时,定位曲线如图1(b)所示。可见,基线越长,定位精度越高。

图1 双站时差频差定位误差
图2显示的是接收站速度[0, 200, 0] m/s、运动辐射源目标速度[0,-100,0] m/s时的定位误差曲线。其他条件与图1相同。图2(a)显示的是基线长度40 km时的仿真图。图2(b)显示的是基线长度100 km时的误差仿真图。由图可以看出,纵向飞行时,在法线方向,2个接收站的频差为零,因而在法线方向上形成定位盲区。
通过仿真对航迹滤波算法进行验证,同时比较EKF和UKF的滤波性能。图2显示的是辐射源速度[200,-150,0] m/s,载机平台为固定平台,时差误差40 ns,频差误差50 Hz时的航迹跟踪示意图。由图2可见,UKF和EKF均可达到较好的跟踪效果。
图2(b)显示的是辐射源速度[150,-150,0]m/s,载机平台运动方向负y轴,速度50 m/s,时差误差40 ns,频差误差50 Hz时的航迹跟踪示意图。

图2 双站时差频差定位误差
上面主要给出了在无点迹的情况下,利用测量的参数直接进行航迹滤波的方法和仿真。图3给出了利用时差频差方法对定位目标进行航迹滤波的示意图。在实际应用环境下,通常先对目标进行定位点的解算,在得到点迹信息的参考下,进行航迹滤波。因为在无定位点迹的情况下,如果首点及定位参数估计或测量不够准确,航迹会出现偏离。因而,需要求解定位目标的点迹,通过点迹可以更好地对航迹跟踪参数进行确定。
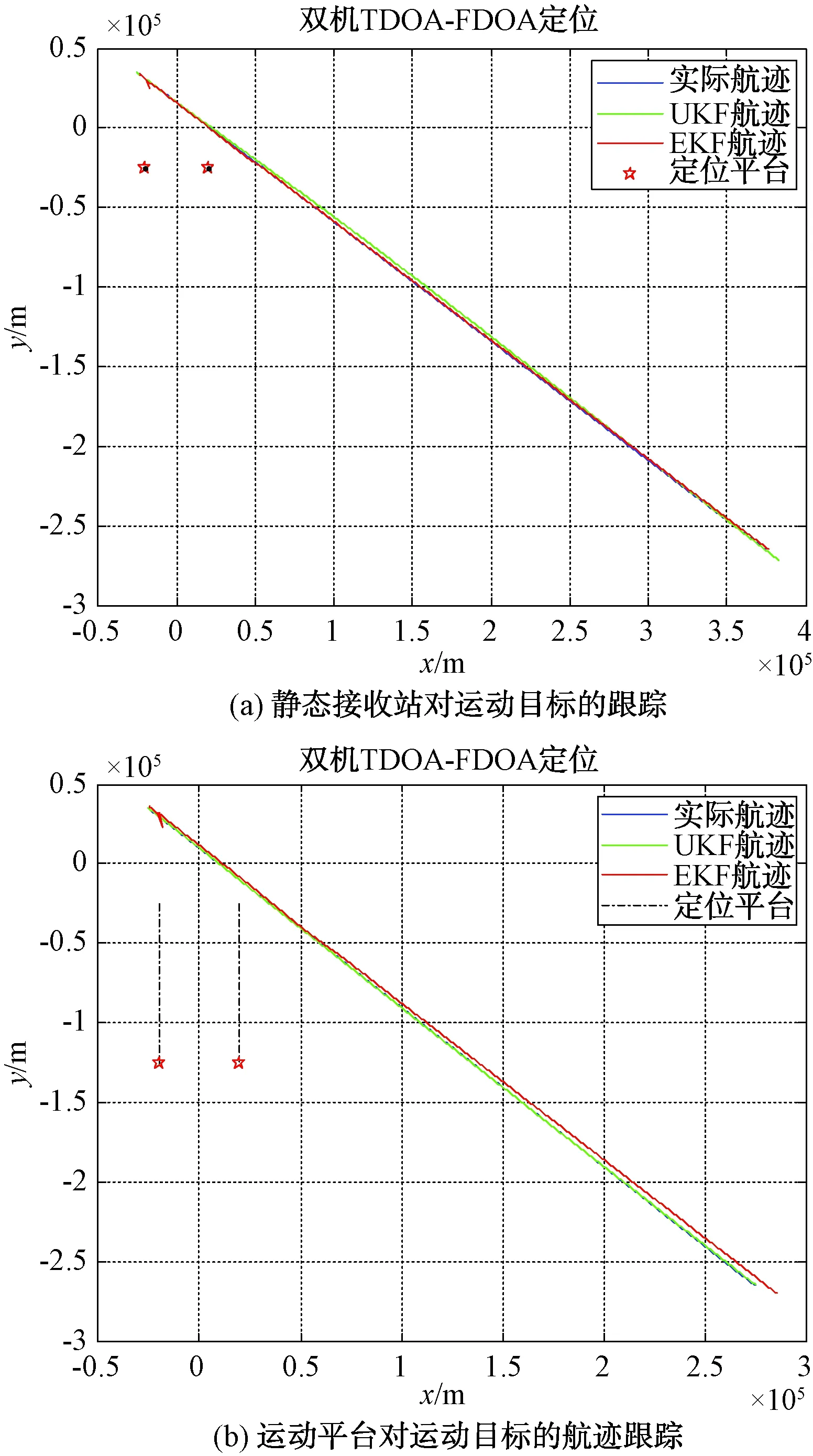
图3 时差频差法对定位目标进行航迹滤波
5 结束语
由于双机协作容易实现,组队灵活性好,因而在战场环境下更容易实现。本文介绍了双机时差频差定位及航迹跟踪方法。首先对时差频差定位原理进行了介绍,然后对时差频差定位精度进行了分析与仿真,最后介绍了基于扩展卡尔曼滤波和无迹卡尔曼滤波航迹跟踪算法,并通过仿真对2种跟踪算法进行了对比。

