基于时差解相位干涉仪模糊的测向方法研究

亓 亮，束 坤，李 迪

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225101)

0 引 言

相比于传统的比幅测向系统的精度差、体积大等缺点，相位干涉仪测向系统具有精度高、体积小等优点，在多种平台下得到广泛使用。由于相位干涉仪的鉴相器只能输出(-π,π)范围内的相位值，要求干涉仪基线长度小于半波长，否则会出现2π的整数倍的相位模糊，但为了提高测向精度，要求相位干涉仪的基线长度尽可能长。通常使用多基线干涉仪来解决这一矛盾，使用短基线干涉仪决定无模糊测向范围，使用长基线决定干涉仪的测量精度。在宽频带测向系统中，高频段波长较短，相应天线受到物理尺寸的限制很难满足基线距离小于半波长的条件，因此通常采用虚拟基线法，形成基线长度比为2k(k=1,2,…)谐波式干涉仪，由短基线逐次解长基线模糊，最终得到无模糊的高精度的来波方位[1]。针对多基线干涉仪系统复杂的缺点，本文研究了在单基线相位干涉仪的基础上，通过获得基线间信号波前的到达时间差来解干涉仪模糊的方法。

1 时差测向基本原理及精度分析

时差测向以其原理简单、测向精度高而很早就被提出来了,但是由于这种方法需要测量非常小的时间间隔,虽然也有不少人对该技术进行过研究，但所做的系统也很难达到较高的测量精度。随着现代大规模集成电路和数字电路的应用,现在时间测量的精度在逐步提高，时差测量的精度能达到1 ns甚至更高,这为广泛应用短基线时间测向法奠定了基础。

1.1 时差测向基本原理

如图1所示，时差测向系统由2个通道组成，2个天线之间的距离l为基线长度，当平面波信号从与天线视轴夹角为β的方向入射时，信号波前到达2个天线的距离差为Δl，可以求出：

Δl=lsinβ

(1)

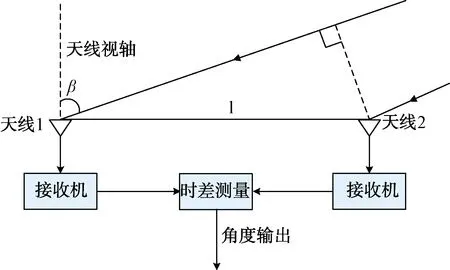
图1 时差测向系统原理框图

根据电磁波在空间的传播速度c，可以得到信号波前到达2个天线的时间差τ，即:

(2)

如果得到时间差，就可以求出信号到达角β，即:

(3)

从式(3)可以看出，由于电磁波空间传播速度c为常数，而基线距离l为一固定值，因此，信号到达角是时间差的函数。

1.2 时差测向精度影响因素分析

为了分析测角误差，对式(2)求微分，得到:

(4)

由于l基本保持不变，而c为一固定常数，因此可以得到：

(5)

求解dβ，得到：

(6)

将式(6)用增量形式，得到：

(7)

根据式(7)可以看出，基线长度l越大，测向误差Δβ越小，所以基线长度应尽可能大，但是受到安装平台的限制，基线长度不可能无限大；同时，测向误差Δβ还和信号到达角β有关，β=0°时，测向误差Δβ最小，β=90°时，测向误差Δβ无穷大，已无法完成测向，因此，干涉仪视角不宜过大，通常选择为β=±45°；此外，测向误差还和时差测量误差有关，时差测量误差影响因素较多，主要和时差测量的方法有关，目前时差测量的方法有前沿检测法和相关检测法。

在β=±45°范围内，测向误差均方根为：

(8)

取基线长度l=10 m，时延误差Δτ=1 ns，则测向误差均方根Δβrms=1 ns。

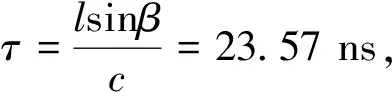
(1)自适应门限处理法：对接收设备的中频信号，经过高速A/D采样后，信号处理尽量利用整个脉冲的前沿，而不是利用脉冲的某个时刻去计算时间差。在计算时差时，采用自适应门限的方法对前沿门限进行处理。不同接收通道设备利用自身接收到的信号前沿的中心作为门限判别的基准，以提高测时精度，降低通道一致性的影响。

(2)相关法：对接收到的中频信号进行高速A/D采样，根据系统情况选择滑窗，采用相关法进行时间差的测量，相关函数最大值对应的延迟量为信号的时延。该方法可以降低测量信噪比的要求，提高系统灵敏度。

2 时差解相位干涉仪解模糊方法

当相位干涉仪基线长度大于半波长时，会存在测向模糊的问题，下文将说明通过时差测量解干涉仪模糊的方法。

2.1 相位干涉仪测向基本原理

将图1中的时差测量模块换为鉴相器，再添加一个角度变换模块，就得到相位干涉仪测向系统，如图2所示。

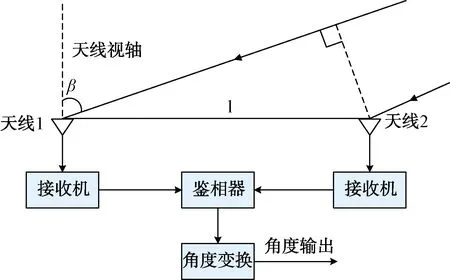
图2 相位干涉仪测向系统原理框图

由入射信号的时差引起的相位差为：

(9)

已知测角相位差φ，就能得到信号到达角β：

(10)

对式(9)求微分得到：

(11)

用增量表示：

(12)

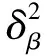
(13)

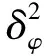
由公式(13)可知，当相位方差一定时，信号到达角估计方差与基线长度的平方成反比，因此可以通过增加基线长度来提高测向精度[2]。由于鉴相器是通过求反正切函数得到相位，只能输出(-π,π)范围内的相位值，当基线长度大于半波长时，鉴相器输出的相位值φ可能存在2π的整数倍模糊，即：

φ=φ+2πm

(14)

式中：m为整数，是基线的相位模糊数，要得到相位的准确值φ，需要求解m，即解相位模糊。

2.2 时差解相位干涉仪模糊方法

解模糊的方法有很多，常用的有长短基线法、参差基线法、虚拟基线法等[3]。长短基线法要求有间距小于信号半波长的基线存在，在宽带测向系统中，高频段的信号波长较短，小于其半波长的基线通常物理上难以实现；参差基线法和虚拟基线法解决了短基线长度受限的问题，但是参差基线法要求基线距离互质，天线摆放形式单一，且容易解模糊失败，虚拟基线法为保证测量精度，所需基线距离越长，则需要越多的次长基线辅助解模糊，对通道一致性要求就越高。基于时差解相位干涉仪模糊的方法只需单基线就能实现解模糊，且测向精度只和基线长度有关，工程实现简单方便。

2.2.1 时差解相位干涉仪原理

2.2.2 正确解模糊所需时间差测量精度分析

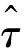
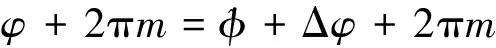
(15)

解m，得到：

(16)

(17)

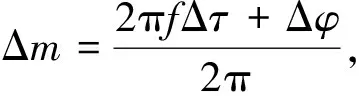
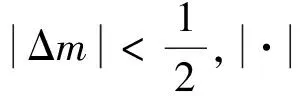
在相位差测量误差Δφ为零的前提下，要保证正确解模糊，不同信号频率下所要求的时间差测量误差Δτ的最大值如图3所示。

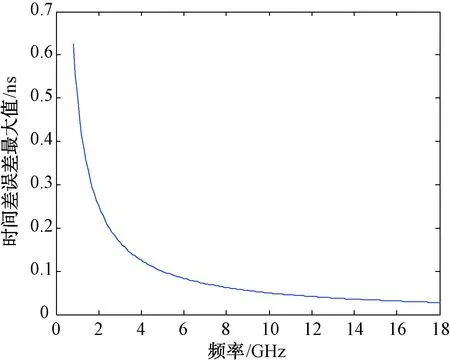
图3 不考虑相位差误差时正确解模糊所要求的时间差误差最大值

从图中可以看出，在不考虑相位差测量误差时，频率越高，保证正确解模糊所需的时间差误差最大值越小，即对时间差测量精度要求越高。当频率为0.8 GHz时，要求时间差测量误差应小于0.625 ns；当频率为18 GHz时，甚至要求时间差误差应小于0.028 ns。

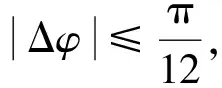
图4 考虑相位差误差时正确解模糊所要求的时间差误差最大值

显然，这比不考虑相位差测量误差时，对时间差的测量精度要求更高，当频率为0.8 GHz时，要求时间差测量误差应小于0.573 ns，当频率为18 GHz时，要求时间差测量误差应小于0.026 ns。

2.2.3 不能正确解模糊时对方位测量精度的影响

表的取值和|Δm|及|Δτ|的关系

表的取值与方位测量精度的关系

表3 基线长度与方位测量精度的关系

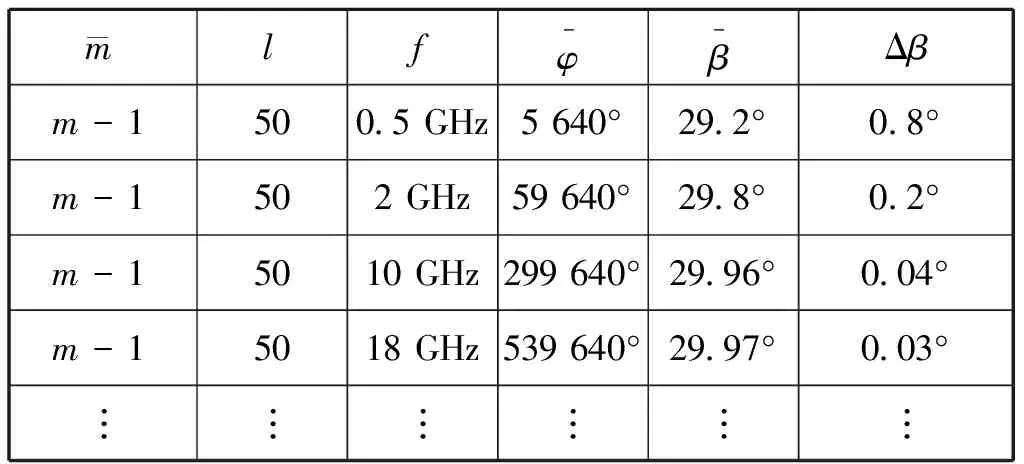
表4 频率与方位测量精度的关系

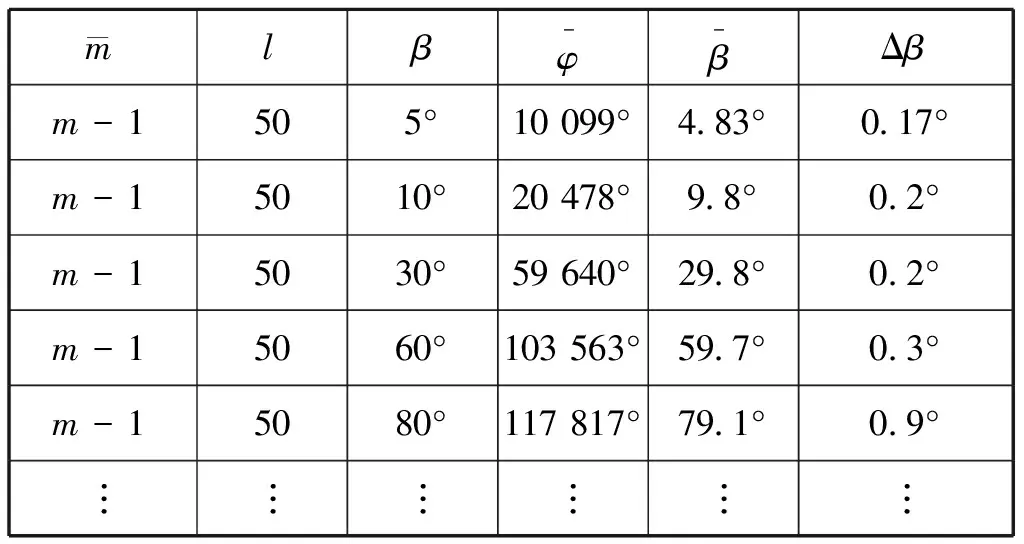
表5 方位角与方位测量精度的关系

根据以上分析，当由于时间差测量精度不足导致无法正确得到模糊数时，根据错误的模糊数无法得到精确的方位角，但是当基线长度较长时，而错误模糊数与真实模糊数差距不是很大时，根据错误模糊数得到的方位测量精度能够满足工程要求，因此根据时间差测量来解相位干涉仪的方法在工程上是可行的。

3 结束语

相位差和时间差存在线性关系，时差测向系统和干涉仪测向系统的本质是一样的，仅仅是使用的估计量不同。相位测量的精度可以到达很高，但是基线长度大于信号半波长时，存在相位模糊。本文分别分析了时差测向系统和相位干涉仪测向系统，研究了通过时间差的测量得到对应的相位差并基于此相位差解干涉仪模糊的方法，分析了正确解干涉仪模糊所需的时间差精度，还分析了时间差精度不足以正确解相位模糊时对方位测量精度的影响，认为在基线长度较长时，如果错误模糊数和正确模糊数差距不是很大，方位测量精度能够满足工程需求。通过时差解干涉仪模糊实现测向的方法，用1条基线2个天线就可以完成一维测向，接收机数量少，设备体积、功耗、重量都能得到降低，在工程实用中具有很大的前景。