一种新的模糊社交网络中心性分析方法

袁国强, 徐建民, 刘明艳

(1. 河北大学 管理学院, 河北 保定 071002;2. 河北金融学院 基础部, 河北 保定 071051;3. 河北大学 网络空间安全与计算机学院, 河北 保定 071002)

1 背景介绍

近年来,国外的Facebook、Twitter以及国内的新浪、腾讯和网易微博等在线社交网络为在线用户及时发布和共享有关日常生活、教育、新闻消息和重大事件等各种信息提供了重要的在线交流平台.研究社交网络中用户的各种交互行为对于分析社交网络具有极其重要的作用,因此,有效合理分析用户间的各种交互行为数据并确定用户的中心性地位已经逐渐成为当前社交网络分析研究中的热点问题.

社交网络中心性分析问题一直是社交网络研究中的重要问题之一.在经典的社会网络研究中,一般采用确定性的图论方法对网络进行建模,图论模型中的结点代表用户,边代表用户之间的连接.一些学者已经采用点度中心性、紧密度中心性、介数中心性和特征向量中心性等方法[1-2]研究社交网络的拓扑结构[3-4].另外,通过这些经典方法不但可以研究社交网络特征,也可用于部分算法的研究.2002年,Girvan等[5]基于介数中心性设计了一种寻找社交网络社区边界的搜索算法.2013年,Badie等[6]利用紧密度中心性发展了一种能够检测复杂社交网络中重叠和非重叠社区结构的新算法.在上述经典的社交网络分析研究中,众多学者主要关注了网络的拓扑结构,并且这种由确定性图论方法得到的研究成果在一定程度上淡化了用户间交互行为所带来的模糊关系,然而,这样的模糊关系在很大程度上会对网络的中心性研究带来很大的影响,尤其当前的社交网络不同于以往的社会网络,由于用户的在线活动一般具有不可预测性、不确定性和时间多变性等特点,因此使用确定性图论方法建立的模型无法有效合理分析大多数的现实社交网络问题.基于以上分析,为了处理当前社交网络中由用户交互行为和时间变化产生的部分不稳定性因素,本文将采用模糊集理论来对社交网络中的用户行为进行分析和建模.自从1965年Zadeh[7]首次提出模糊集的概念以来,许多学者在管理科学[8]、金融工程[9]、网络分析[10]和生物医学[11]等诸多领域运用模糊方法进行了大量的研究工作,并取得了可喜的成果.正是由于模糊方法在现代科学研究中的广泛应用,从而也使得模糊社交网络中心性分析问题的研究工作得到了很好的发展.廖丽平等[12]基于模糊方法定义了模糊结点中心度、模糊紧密中心度和模糊间距中心度等概念.岳振军等[13]提出了一种新的由自然语言表述的模糊关系社会网络,并研究了其中心性分析问题.Hu等[14]利用模糊方法讨论了有向社交网络中的点度中心性和接近中心性问题.Lu等[15]对于人际空间关系问题建立了一类模糊社交网络的中心性分析模型.2018年,Wu等[16]利用区间二型模糊集理论解决了复杂和不确定社交网络中的大规模群决策问题.鉴于上述模糊社交网络中心性问题的研究,现有文献中模糊结点度均采用了该点连接边的隶属度求和方法,该方法主要源于确定性社交网络中心性分析中点度中心性的计算方法,主要目的是利用与结点相连接结点的数量来确定结点的中心性.然而,当社交网络中用户间边的权重设置为隶属度仍沿用确定性图论中的中心性确定方法,就会显得与现实存在一定偏差,原因在于简单隶属度求和有时并不能完全代表该结点在模糊社交网络中的中心地位.

为了进一步寻求更加有效的结点中心性的度量方法,本文将采用可信性理论对社交网络的结点中心性进行分析建模.可信性函数是Liu等[17]在2002年基于可能性测度提出的一类具有自对偶性质的函数.近十几年来,可信性理论不但有效丰富了模糊集理论,而且已经在经济、管理、工程和生产等各个领域得到了广泛应用[18-21],尤其是2006年高晓沨[22]在硕士论文中基于可信性理论研究了几类新的可靠性网络的拓扑优化模型.与文献[22]不同的是,本文主要工作在可信性理论基础上建立一种新的模糊社交网络中心性分析模型.

2 基本概念

美国控制论学家Zadeh[7]利用隶属函数首次提出模糊集的概念.随着模糊集理论的发展,Zadeh[23]进一步提出了可能性测度用来度量模糊事件的大小.在过去的几十年中,可能性理论已经在模糊决策、模糊关系和模糊控制等领域得到了广泛的发展和应用,但是自对偶性质的可能性测度在理论和应用方面仍需进一步完善.基于此,Liu等[17]在2002年提出了一类具有自对偶性质的可信性测度.下面首先回顾一下模糊集、可信性理论和模糊图中的一些基本概念.

给定一个论域Γ,Pos是一个定义在幂集Ρ(Γ)上的集函数.若Pos满足条件:

1)Ρos(Φ)=0,Ρos(Γ)=1;

基于可能性测度Pos,Liu等[17]定义了具有自对偶性质的集函数Cr.

定义2.1设三元组(Γ,P(Γ),Pos)是一个可能性空间,若

A∈P(Γ),

则称集函数Cr是事件A的可信性测度,其中Ac是集合A的补集,这里,称三元组(Γ,P(Γ),Cr)是一个可信性空间.

定义2.2[24]在有限图G=(V,E)中,对每条边赋以(0,1]中的数值作为权重,即规定一个权函数

μ:E→(0,1],

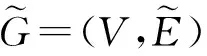
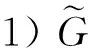
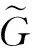
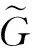
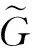
5) 顶点vi和vj之间的连通强度S(vi,vj)定义为

其中Lvi,vj表示vi和vj之间的所有通路.

关于模糊集、可信性理论和模糊图的更多知识可以参阅文献[24-26].

3 模糊社交网络中心性的计算方法

在实际的社交网络中,用户(结点)之间一般不会相互独立,而是彼此之间通过各种交互行为(边或链接)连接起来.与普通社会网络不同的是,当社交网络用户之间建立连接后,他们之间就会相互影响.更确切地说,用户之间的影响程度大小是社交网络中用户间亲密度的一种表现,这种影响力可以增强或减弱.若沿用经典的社会网络方法研究社交网络,不足之处在于原有方法注重网络的拓扑结构,这样就不能很好地体现用户之间由交互行为而产生的亲密度强弱关系.基于此,本文采用模糊方法处理社交网络中用户之间连接的亲密度关系,并有效确定用户在整个网络中的中心影响力.为了给出模糊社交网络的相关概念,首先给出符号说明(见表1).

表 1 符号说明Tab.1 The description of symbol

3.1模糊结点中心性和紧密中心性设社交网络中存在n个用户,并且用户之间存在m(0mn(n+1))条边,分别表示为V和E.当社交网络中存在模糊因素时,用户vi和vj之间的连接(亲密度)用边表示,交互信息也可以由用户vi通过边传递给用户vj,同时,传递边在这样的模糊社交网络中则带有1个以隶属度定义的权重来表示用户vi和vj之间的亲密度，因此,模糊社交网络的相关定义如下.

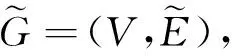
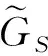
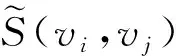
上面已经给出了模糊社交网络的相关定义,而在实际社交网络中人们关心的是哪些用户对于整个网络的影响力更大,因此,要想度量某个用户的影响力,仅仅定义模糊社交网络显然还不够.一般来说,经典的社会网络中1个结点的重要性与该结点的连接结点的数量存在必然联系.换句话说,1个结点的连接结点数量越大,该结点就越重要,并且网络的中心地位就越高.在社会网络中,利用经典图论分析结点影响力一般采用结点度的定义.由于模糊社交网络的特殊性,简单套用原有结点度定义是不可行的.在模糊社交网络中,边的意义是用户间的交互亲密度的体现.一般来说,1个用户的重要性与该用户连接用户的整体亲密度有关系,即用户的整体亲密度越大,该用户在网络中的位置就越重要,信息通过该用户传播的可信性越大.本文将采用可信性理论评价用户网络影响力(结点中心度),因此,模糊社交网络的用户(结点)中心度定义如下.

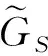
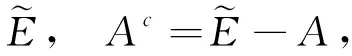
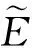
在现实社交网络中,与非中心用户相比,1个中心用户应该将信息传递给网络其它用户的可信度更高.一般社会网络中,紧密度中心性用于评价1个用户到其它所有用户的紧密程度,而模糊社交网络采用模糊紧密中心性来说明中心用户传递信息的可信程度.模糊紧密中心性需要计算某个用户向网络其它用户传递信息可信度的平均值,定义如下:

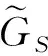
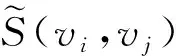
3.2模糊社交网络中心度数值算例为了说明本文所设计模糊社交网络中心性分析方法的有效性,下面分别给出经典社会网络和模糊社交网络的结点中心度和紧密中心度数值算例.通过比较2个例题的计算结果,分析不同网络中的中心度,从而说明本文提出的中心度计算方法具有一定的现实意义,方法也是有效和可行的.

例3.1图1是1个经典无向社交网络,它有9个结点vi(i=1,2,…,9),12条边e12、e13、e14、e23、e35、e36、e37、e39、e56、e67、e68、e89,下面运用经典的中心性分析方法计算各结点的中心度.

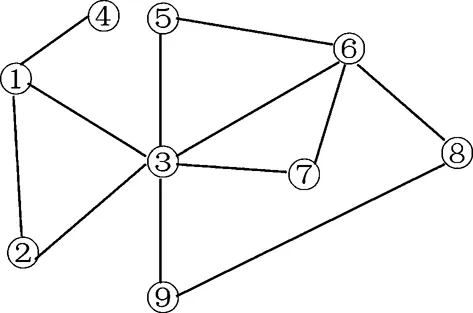
图 1 经典社交网络图

解根据经典的社会网络中心性方法[27]可得以下结论.

1) 结点中心度:

CD(v1)=3,CD(v2)=2,CD(v3)=6,

CD(v4)=1,CD(v5)=2,CD(v6)=4,

CD(v7)=2,CD(v8)=2,CD(v9)=2.

2) 紧密中心度:

解由于其它模糊社会网络的紧密性中心度计算时需要选择距离公式,不同的距离公式会产生不同的结果,从而不具有可比性,因此,下面根据文献[12]仅计算结点中心度,且由本文提出的方法计算结点中心度和紧密性中心度.

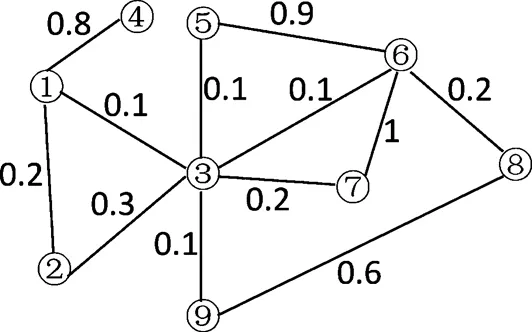
图 2 模糊社交网络图

1) 传统模糊社会网络的结点中心度:

2) 本文方法的结点中心度:

3) 本文方法的紧密性中心度(仅以结点v1和v2为例):

分析例3.1和例3.2可以看出:

1) 从结点中心性的角度看,例3.1中结点v3的中心度最大,是因为与其相连接的结点数量最大.但是,在例3.2的模糊社交网络中,结点v3的模糊中心度并不是最大的,而结点v6的模糊中心度是最大的.计算结果说明传统社会网络的中心性分析方法并不能完全解决模糊社会网络的中心性分析问题.

2) 在传统模糊社会网络中,结点v3的中心度排名第四,而利用本文提出的方法计算结点v3的中心度排名最小.从图2可以看出,虽然与结点v3相连接的结点数量最多,但是边的权重却很小,也说明这些结点与结点v3的亲密度很小,而其它结点连接边的权重相对结点v3都比较大,所以利用本文的方法可以有效地区分出各个结点的中心度大小,并说明本文方法是可行的.

4 结论与展望

本文的主要工作如下:

1) 基于可信性理论给出新的模糊社交网络的概念以及结点连通强度、模糊结点中心度和模糊紧密性中心度的定义.

2) 通过数值算例说明模糊结点中心度的合理性,并对本文提出的方法进行了有效性和合理性的验证.

下一步工作的展望:

1) 本文虽然给出了模糊结点中心度和紧密性中心度的计算方法,但是没有进一步对介数中心性和特征向量中心性等其它中心性问题进行分析,因此,这些问题将是本文下一步工作的1个主要研究方向.

2) 本文给出了2个数值算例对模糊社交网络的中心度进行了计算,但是该方法还有待进一步进行实际社交网络的验证,因此,在各种微博网络、在线社区平台、在线讨论区等社交网络平台进行实验研究也是本文下一步的主要工作方向.