量子密集编码的理论研究进展

莫智文, 杨 雪, 江雨婷, 柏明强

(四川师范大学 数学与软件科学学院, 四川 成都 610066)

量子纠缠在量子信息论中处于核心地位,在量子密集编码、量子隐形传态、量子密码术和量子安全直接信等领域有着重要应用.而量子密集编码作为体现量子纠缠特性最引人瞩目的应用之一,是Bennett等[1]在1992年提出的.量子密集编码用经典比特表示信息,利用量子纠缠态的非局域关联特性,借助于量子信道实现发送1个量子比特、传递2个比特的经典信息，引起了广大学者的研究兴趣.最初的密集编码方案大多采用Bell态[1-2]或者二粒子纯态[3-4]作为量子信道.然而随着量子密集编码研究的深入,文献[5-10]已经将双方推广到了多方,纯态推广到了混合态.Liu等[9]将多方密集编码方案的量子信道由二能级粒子纠缠态推广到任意能级粒子纠缠态.在以往的协议中,量子密集编码采用的是有限维Hibert空间的量子信道，现在人们可以在无限维Hibert空间中用量子态进行密集编码[11].Hao等[12]在原始密集编码的基础上增加了1个控制方的受控密集编码,紧接着,学者们又以GHZ态为量子信道的受控密集编码方案,推广到基于不同纠缠信道的受控密集编码[13-27].在2010年,Situ等[28]提出了1个发送者多个接收者的同时密集编码方案,该方案分别以Bell态、GHZ态和1种特殊的W态为量子信道设计编码协议.后来,Zhang等[29]提出了基于四粒子Cluster态的同时密集编码协议,Huang等[30]分析了量子态在退相干的情况下,同时密集编码协议的性能表现.在2014年,Situ[31]又提出了基于GHZ态的受控同时密集编码方案.2018年,Hu等[32]在量子密集编码研究中取得新进展,该团队李传锋、柳必恒等人首次利用四维纠缠态实现量子密集编码,达到2.09的信道容量,创造了当前国际最高水平.本文将总结已有的一些研究成果,并对其未来的研究方向给予展望.

1 预备知识

量子比特(即量子位)是量子信息中的量子系统,是经典比特的量子对应,但又不同于经典比特.1个量子比特系统是1个二维Hibert空间,或者说是1个双态量子系统.在经典情况下,系统只能处于2个状态中的1个,即1或0,而在量子情况下,系统既可以是处于|1〉或|0〉,也可处于叠加态

|ψ〉=a|0〉+b|1〉,

(1)

其中,a,b∈C且满足|a|2+|b|2=1,{|0〉,|1〉}是二维Hibert空间的一组完备正交基.量子比特以|a|2的概率处于状态|0〉和以|b|2的概率处于状态|1〉,这便是量子态的不确定性与叠加性.通过确定a和b,可以在1个量子比特中编码无穷多的信息.显而易见,2个量子比特构成的系统是1个四维Hibert空间,{|00〉,|01〉,|10〉,|11〉}是Hibert空间的一组完备正交基,双量子比特也可处于这组基态的多种叠加态

|ψ〉=a00|00〉+a01|01〉+

a10|10〉+a11|11〉.

(2)

量子态|χ〉(χ=00,01,10,11)出现的概率为|aχ|2,且|a00|2+|a01|2+|a10|2+|a11|2=1.以此类推,n个量子比特系统可以是1个2n维Hibert空间,系统所处状态是该空间中的1个向量,系统的状态可以是2n个相互正交的态的叠加态.需要指出,两量子比特系统的完备正交基可以由单量子比特系统的完备正交基通过张量积运算得到,{|00〉,|01〉,|10〉,|11〉}就是由{|0〉,|1〉}得来.类似地可以求得任意n个量子比特系统的完备正交基,进而表示出n个量子比特的叠加态.当量子比特列的叠加态无法用各量子比特的张量积表示时,这种叠加态就称为量子纠缠态.例如有一量子叠加态

(3)

但是对于量子叠加态

(4)

无论采用怎样的方法都不能写成2个量子比特的乘积.简单的数学解释为:假设在2个子系统A和B组成的复合系统中,如果复合系统的1个量子纯态不能表示成A、B这2个子系统纯态的直积态,即|ψ〉AB≠|ψ〉A⊗|ψ〉B,那么这个态就是1个量子纠缠态.在多个复合量子体系中,只要多个子系统处于量子纠缠态,无论这些子系统距离有多远,都不能被看成是相互独立的.量子纠缠可形象比喻为生活中女孩子的小辫子,小辫子中的任何一绺状态发生变化都会影响其他辫子的状态.

常见的量子纠缠态有以下几种.

1) Bell态:

(5)

2) GHZ态和W态:

(6)

3) MS(Maximal Slice)态:

|MS〉=

4) Cluster态:

|C4〉=

量子测量除了是量子力学的基本问题,还在量子信息和量子计算理论中占有重要的地位.与经典物理中的测量不同,量子测量不是独立于所观测的物理系统而单独存在的,它本身是物理系统的一部分.在理想情况下经典测量不会干扰被测量的态,而量子测量则会改变被测系统的态.量子测量假设可以进行如下描述:量子测量由一组测量算子{Mm}构成,作用在被测系统状态空间上的算子,指标m代表实验中可能出现的测量结果.如果测量前系统的态由|ψ〉表示,那么测量后得到结果m的概率为:

(9)

且系统状态变为:

(10)

测量算子满足完备性方程

(11)

该方程表达了概率和为1的事实:

(12)

这在量子信息中称为广义测量(general measurement),它的一个重要应用就是区分量子态.广义测量包含有2种特殊情况:投影测量(PM)和正算子值测量(POVM).投影测量是指测量算子Mm是厄米的(即Mm是正交投影算子),且满足MmMm′=δm,m′Mm的广义测量.

广义测量的另外一种特殊情况是正算子值测量.正算子值测量(POVM)是比正交投影测量更一般的量子测量[33],POVM更关心测量结果的概率,并不关心测量后系统的状态.由量子态不可克隆定理知道,量子非正交态不能被确定性区分,这时可以用POVM测量来进行概率性区分量子态.区分2个非正交态|ψ1〉=α|0〉+β|1〉和|ψ2〉=α|0〉-β|1〉为例,可以构造3个POVM算子:

(13)

其中

I为恒等算子,且与α和β相关的参数ω应使E3为半正定算子.为了确定ω,可将3个算子改写成：

(14)

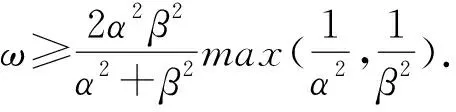
POVM不像正交投影测量那样可以给出1个和经典类比直观的物理图像.正交投影测量在实验上较容易实现,与正交投影测量相比,POVM中可以存在不互相正交的测量结果,因而理解和实现POVM都相对困难.

2 Bennett量子密集编码方案

Bennett等[1]提出了两方量子密集编码方案.假设信息发送者Alice和接收者Bob共享的量子信道为最大纠缠态

(16)

Alice对其拥有的粒子进行以下4种不同的标准Pauli酉操作之一,

(17)

这个操作实际上分别是对2个比特的经典信息00,01,10,11进行编码,这里定义

|φ(xy)〉=

(18)

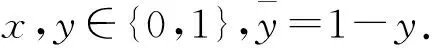
Alice将粒子A发送给Bob,Bob对粒子A,B施行Bell基测量((5)式),测量结果可使Bob知道他拥有的量子比特对的状态.

由于在测量之前Alice和Bob约定如下编码规则:φ(00)→00,φ(01)→01,φ(10)→10,φ(11)→11,故通过Bell基测量,Bob就能知道发送者所要传递的经典信息,并获得由Alice传送的2个比特的经典信息;因此Alice仅发送1个量子比特给Bob,便能成功传送2个比特的经典信息,这就是所谓的量子密集编码.

3 多方量子密集编码

Bennett量子密集编码方案考虑1个发送方和1个接收方.1998年,Bose等[5]将密集编码方案推广至多方信息传输过程.该方案利用N+1粒子的最大纠缠态作为量子信道进行N+1方信息传输,其中N方为信息发送者,一方为信息接收者,假定N+1方各拥有处于最大纠缠态中的1个粒子,其中1个发送者对其拥有的粒子施行I、σX、iσY和σZ这4种可能的酉操作之一,其余N-1个发送者各施行I,σX这2种可能的酉操作之一,这样对N个粒子能够施行的独立的酉操作个数为4×2×2×…×2=2N+1;然后发送者把粒子传送给接收者,接收者对N+1个粒子进行测量,根据测量结果能够判断出由所有发送者施行的酉操作的组合,进而获得N+1比特的信息.

3.1基于非最大纠缠态的多方概率密集编码

3.1.1三方信息传输的概率密集编码方案 下面以非最大纠缠态作为量子信道为例,说明如何实现这种多方概率密集编码协议[34].假设Alice和Bob为信息发送者,Cliff为信息接收者,他们拥有3粒子部分纠缠态:

|Φ0〉123=α|000〉123+β|111〉123,

(20)

其中系数均为非零实数，且满足α2+β2=1,α<β.粒子1,2,3分别属于Alice、Bob和Cliff.具体步骤如下.

1) Alice对粒子1施行I、σX、iσY和σZ这4种不同的酉操作之一,Bob对粒子2施行I和σX这2种不同的酉操作之一.

(21)

经过酉操作,粒子1,2,3的状态由|Φ0〉123相应变为

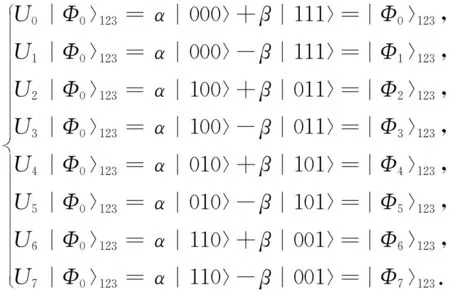
2) Alice将粒子1,Bob将粒子2分别传送给Cliff,Cliff事先准备好1个辅助粒子a,初始态为|0〉a.Cliff在1组正交基{|00〉3a,|01〉3a,|10〉3a,|11〉3a}下对粒子3和辅助粒子a施行联合酉变换

则对粒子1,2,3和辅助粒子a的总的酉操作为U=I⊗Usum,I为4×4的单位矩阵,作用结果为

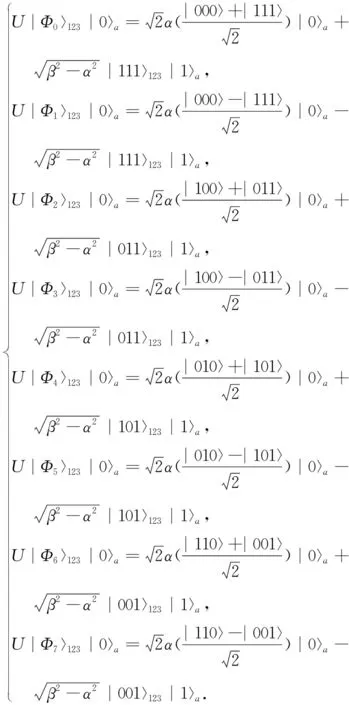
3) Cliff对辅助粒子a进行测量,若测量结果为|0〉a,粒子1,2,3将塌缩到某一确定的GHZ态,然后通过对粒子1,2,3进行GHZ态测量,测量基为:

(25)

测量之后Cliff就知道Alice和Bob所做的酉操作类型,从而密集编码获得成功,Cliff获得3比特信息,密集编码成功概率为2α2;若测量结果为|1〉a,粒子1,2,3处于直积态|111〉,|011〉,|101〉,|001〉中的1个,Cliff无法根据测量结果判断出Alice和Bob所施行的酉操作类型,密集编码失败.但此时并不是说Cliff完全不能从中获得信息,他可以根据测量结果判断出Alice和Bob施行的酉操作是属于{U0,U1},{U2,U3},{U4,U5}和{U6,U7}中的哪一组,从而获得2比特信息,概率为β2-α2.在此方案中,Cliff获得的平均信息量为

Itrans=

2α2×3+(β2-α2)×2=2+2α2,

(26)

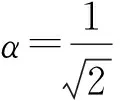
3.1.2N+1方之间的概率密集编码方案 三方非最大纠缠态的概率密集编码方案可以推广到N+1方,N方传送,一方接收,其中1个发送者对其拥有的粒子施行I、σX、iσY和σZ这4种可能的酉操作之一,其余N-1个发送者各施行I,σX这2种可能的酉操作之一,这样对N个粒子能够施行独立酉操作个数为4×2×2×…×2=2N+1,所有发送者分别对手中的粒子做相应的酉操作后,将粒子传送给接收者,接收者事先准备好1个辅助粒子,然后对手中原有的粒子和辅助粒子做联合酉操作Usum,对其他所有粒子作恒等变换,即U=I⊗Usum,I是2N×2N单位矩阵.做了变换之后接收者对辅助粒子a进行测量,若测量结果是|0〉a,再对另外N+1个粒子进行测量,根据测量结果判断出所有发送者施行的酉操作类型,获得N+1比特信息,密集编码成功,成功概率为2α2;若测量结果为|1〉a,则接收者无法根据测量结果判断出发送者所施行的酉操作类型,密集编码失败.但此时他仍可以根据测量结果获得N比特信息,概率为β2-α2,在此方案中接收者获得的平均信息量为

Itrans=2α2×(N+1)+

(β2-α2)×N=N+2α2.

(27)

4 受控密集编码

在原始密集编码的基础上增加1个第三方(控制方)的编码方案,称之为受控密集编码.Hao等[12]提出第一个受控密集编码方案.该方案表明当采用GHZ态作为量子信道时,就像在受控隐形传态中保真度取决于控制方的测量一样,受控密集编码中编码成功的概率也由控制方的测量基决定.本节主要针对最原始的受控密集编码方案进行简要介绍,其利用3粒子最大纠缠GHZ态作为量子信道,在第三方控制下,通过引入辅助粒子和做适当的酉变换(纠缠浓缩)，以一定概率实现受控量子密集编码协议,主要介绍受控密集编码方案及控制力度量.

4.1基于最大纠缠GHZ态的受控密集编码假设信息的发送者Alice、接收者Bob和控制者Charlie所处的量子信道为GHZ态,形式如下

|Φ〉123=

(28)

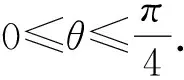
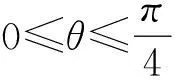
这里,粒子1、2和3分别被Alice、Bob和Charlie所拥有.为了控制Alice和Bob之间的量子信道以及Alice传递给Bob的信息数量,Charlie需要在基{|+〉3,|-〉3}下对粒子3进行投影测量,然后将他测得的结果通过经典信道告诉Alice和Bob,测量基为

|+〉3=cosθ|0〉3+sinθ|1〉3,

|-〉3=

sinθ|0〉3-cosθ|1〉3,

(29)

|Φ〉123=

(30)

这里

|α〉12=cosθ|00〉+sinθ|11〉,

|β〉12=sinθ|00〉-cosθ|11〉.

(31)

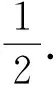
那么总的酉操作U=I⊗Usum就会把态|α〉12⊗|0〉a转化成

|α〉12a=

(33)

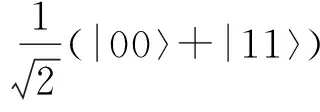
Itrans=1+1×2sin2θ.

(34)

4.2基于部分纠缠MS态的受控密集编码在很多方案中,都是利用粒子的最大纠缠态作为量子信道进行密集编码.在实际中,由于量子信道和周围环境的相互作用,引起信道的消相干是不可避免的,这就导致了最大纠缠态不易保持.鉴于此种情况,利用部分纠缠态作为量子信道来实现概率密集编码的想法便应运而生了.因此选取部分纠缠MS态作为量子信道实现概率性密集编码[25].

假设信息的发送者Alice、接收者Bob和控制者Charlie所处的量子信道为部分纠缠MS态:

cosα|110〉+sinα|111〉),

(35)

|Φ〉123=|φ〉12|+〉3+|ψ〉12|-〉3,

(36)

其中

|φ〉12=

sinθsinα|11〉],

(37)

|ψ〉12=

cosθsinα|11〉].

(38)

Charlie对粒子3进行投影测量的结果为|+〉3或|-〉3,2种结果的概率分别为向量|φ〉12,|ψ〉12模长的平方.

下面讨论另外一种实现密集编码的方式(前面介绍的是经过纠缠浓缩的受控密集编码,在此处也可以采用,过程类似,不再重复),称之为经过广义测量的受控密集编码.首先考虑Charlie的测量结果是|+〉3,|-〉3,其余可类似讨论.Charlie在基{|+〉3,|-〉3}下对粒子3进行投影测量,然后把他测得的结果通过经典信道告诉Alice.在收到Charlie的测量结果之后,Alice直接执行4种酉操作I、σX、iσY和σZ中的1种,从而Alice和Bob之间的共享态就变成如下4种可能的非正交态之一:

|μ1〉12=

|μ2〉12=

|μ3〉12=

|μ4〉12=

(39)

然后Alice把粒子1发送给Bob,从而Bob拥有上述4种可能的量子态之一.以上4种量子态不是相互正交的,由量子态不可克隆定理,无法确定区分量子非正交态;但是,上述4种量子态是线性无关的,这时就可以用POVM测量以一定的概率来区分量子态.为了区分上述的非正交态,Bob首先以P1=|00〉〈00|+|11〉〈11|和P2=|01〉〈01|+|10〉〈10|做投影测量,显然P1和P2是相互正交的.Bob能够知道Alice的操作是{I,σZ}还是{σX,iσY}.若Bob的测量结果是P1,则量子态要么是|μ1〉12,要么是|μ4〉12;若Bob的测量结果是P2,则量子态要么是|μ2〉12,要么是|μ3〉12.投影测量之后,Bob能够得到1比特的信息.假设Bob的测量结果是P1,则他对2量子比特执行正算子值测量(POVM测量).此时在子空间{|00〉,|11〉}构造的POVM元为:

(40)

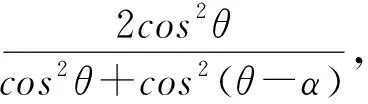
(41)

若Charlie的测量结果是|-〉3,类似计算.此过程平均地从Alice到Bob传递

(42)

比特经典信息.综上可得,密集编码过程中,平均地从Alice到Bob传递

1+sin2(θ-α)+cos2θ

(43)

比特经典信息.以上结果表明,密集编码过程中,信息传输量均优于经典通信.另外,MS态作为量子信道时,控制方并非任意选取,即信道中粒子的地位并非相同.这也是受控密集编码的技巧所在,需要选择合适的信道和恰当的控制方,采用对应的量子操作,才能保证实现真正的密集编码.事实上文献[22]还说明了通过纠缠浓缩与广义测量2种方法实现受控密集编码,接收者获得的平均信息传递量是一样的.

4.3基于扩展的GHZ态受控密集编码的最小控制力之前关于受控密集编码方案大多关注的信息传递量,并未考虑控制方的权威性(Authority)或者控制力(Control power).下面介绍如何度量受控密集编码控制方的控制力[35].

在Bennett提出的原始密集编码方案中,信道为最大纠缠态Bell态,从发送者Alice到接收者Bob之间能够通过发送1个量子比特实现2比特经典信息的传输.当信道为一般2量子比特纯态ρAB时,密集编码的信道容量C(ρAB)定义为

C(ρAB)=1+S(ρB)-S(ρAB),

(44)

其中,Alice和Bob分别拥有量子比特A和B,S(ρ)=-Tr(ρlog2ρ)为冯诺依曼熵.

在受控密集编码方案中,Charlie为控制方,监督和控制Alice和Bob之间的信息传输.此时,信道容量定义如下:

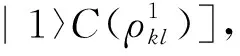
(45)

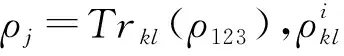
对于没有控制方参与的情形时,Alice和Bob之间共享的量子态为Alice和Bob的约化密度矩阵,记为ρkl=Trj(ρ123),其中Alice和Bob分别拥有第k,l量子比特.无控制方参与时的信道容量为C(ρkl),记为Cj(ρkl),因此,有无控制方参与时的信道容量之差为

(46)

受控密集编码的最小控制力为

(47)

扩展的三粒子GHZ纯态定义为

|ψeGHZ〉123=

λ1|000〉+λ2|110〉+λ3|111〉,

(48)

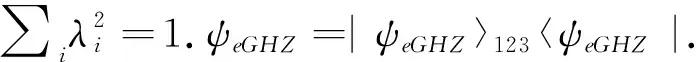
(49)

其中,h(x)=-xlog2x-(1-x)log2(1-x)为二元熵函数,x∈[0,1].在无控制方参与时,通信双方之间的信道容量为:

C3(ρ12)=C3(ρ21)=

C1(ρ23)=C2(ρ13)=

C2(ρ31)=C1(ρ32)=1.

(50)

因此,相应的受控密集编码的CP为:

p132(ψeGHZ)=p231=p312=p321=

(51)

因为

(52)

故当量子信道为|ψeGHZ〉时,控制者Charlie的最小控制力为

p(ψeGHZ)=

(53)

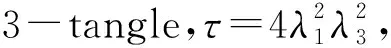
(54)

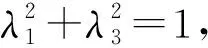
(55)

此时

(56)

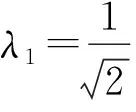
其最小控制力为

(57)

下面是以扩展的GHZ态为受控密集编码的量子信道,计算出了控制方的最小控制力,其纠缠τ与最小控制力P的关系为

并分析了广义GHZ态、标准GHZ态以及MS态作为量子信道时的最小控制力.上述表明,最小控制力与量子态的纠缠有着内在的关联.最小控制力可以刻画量子态的纠缠,同时量子态的纠缠也决定着控制力大小,因为当量子态为最大纠缠GHZ态时,即τ=1时,最小控制力取得最大值1.当量子态能够完全分离时,即τ=0时,最小控制力取得最小值0.那么对于其他量子态作为信道时,纠缠与最小控制力的关系又是怎样的呢?这是需要进一步研究的课题.

5 同时密集编码

多方量子密集编码方案是考虑多个发送者和1个接收者的情形.方案中有1个发送者和多个接收者的密集编码方案称为同时密集编码.现有对同时密集编码的研究大多集中在量子信道的改进,比如Bell态、GHZ态、W型态[28]、四粒子Cluster态[29]和χ型纠缠态[36],这些协议都是在无噪声的情况下设计的.2017年,Huang等[30]研究了在噪声影响下的同时密集编码协议.与此同时,在同时密集编码协议的基础上增加1个第三方(控制方),Situ[31]提出了基于GHZ态的受控同时密集编码协议.此部分主要介绍原始的同时密集编码及受控同时密集编码协议.

⊗

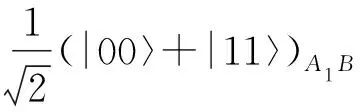
(58)

在这里,粒子A1和A2属于Alice,粒子B、C分别属于Bob和Charlie.

该协议过程分为以下5个步骤:

1) Alice编码:首先,Alice对粒子A1实施酉变换U(b1b2),对粒子A2实施酉变换U(c1c2),复合系统态变为

|ψ(1)〉=

UA1(b1b2)⊗UA2(c1c2)|ψ(0)〉=

|φ(b1b2)〉A1B⊗|φ(c1c2)〉A2C,

(59)

其中,U(xy)及|φ(xy)〉是这样定义的:

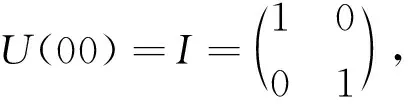
(60)

|φ(xy)〉=

(61)

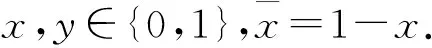
2) Alice加锁.为了锁住纠缠信道,Alice对粒子A1,A2执行傅里叶变换

(62)

复合系统的态变为

|ψ(2)〉=

QFTA1A2[|φ(b1b2)〉A1B⊗|φ(c1c2)〉A2C]. (63)

3) Alice发送粒子A1给Bob,发送粒子A2给Charlie.

4) Bob和Charlie合作对粒子A1,A2执行QFT†,复合系统的态变为:

|ψ(3)〉=

|φ(b1b2)〉A1B|φ(c1c2)〉A2C.

(64)

5) 为了获得(b1b2)和(c1c2),像原始密集编码方案一样,Bob和Charlie分别对粒子A1B和A2C执行Bell基测量,根据先前约定的编码规则,Bob和Charlie分别获得经典比特(b1b2)和(c1c2).

5.2基于GHZ态的同时受控密集编方案下面介绍最初的同时受控密集编码协议[31].Alice打算发送2个经典比特(b1,b2)给Bob的同时,发送另外2个比特(c1,c2)给Charlie,但是必须得到控制者的允许,并且在Bob和Charlie同时合作的情况下,Bob和Charlie才能知道Alice发送的内容.

最初,Alice、Bob和控制者共享GHZ态

|GHZ〉123=

(65)

在这里,粒子1,2,3分别属于Alice、Bob和控制者.

Alice,Charlie和控制者共享另外1个GHZ态

|GHZ〉456=

(66)

这里,粒子4,5,6分别属于Alice、Charlie和控制者.

复合系统的初态为

⊗

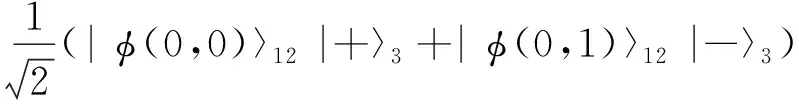
其中

(68)

同时受控密集编码协议具体步骤如下.

1) Alice编码.Alice对粒子1实施酉变换U(b1,b2)来编码比特(b1,b2),对粒子4实施酉变换U(c1,c2)来编码比特(c1,c2),编码之后,复合系统的态

|Ω(1)〉=

U1(b1,b2)⊗U4(c1,c2)|Ω(0)〉=

|φ(b1,b2⊕1)〉12|-〉3)⊗

|φ(c1,c2⊕1)〉45|-〉6),

(69)

U(b1,b2)及U(c1,c2)对Bell态做变换得

U1(x1,y1)|φ(x2,y2)〉12=

U2(x1,y1)|φ(x2,y2)〉12=

|φ(x1⊕x2,y1⊕y2)〉12.

(70)

2) Alice加锁.为了锁住纠缠信道,Alice对粒子1和4执行傅里叶变换QFT,复合系统的态

|Ω(2)〉=QFT14|Ω(1)〉=

QFT14|φ(b1,b2)〉12|φ(c1,c2⊕1)〉45|+〉3|-〉6+

QFT14|φ(b1,b2⊕1)〉12|φ(c1,c2)〉45|-〉3|+〉6+

QFT14|φ(b1,b2⊕1)〉12|φ(c1,c2⊕1)〉45|-〉3|-〉6).(71)

3) Alice发送粒子1给Bob,发送粒子4给Charlie.

4) Bob和Charlie合作对粒子1和4执行QFT,复合系统的态

|Ω(3)〉=QFT14|Ω(2)〉=

|φ(b1,b2)〉12|φ(c1,c2⊕1)〉45|+〉3|-〉6+

|φ(b1,b2⊕1)〉12|φ(c1,c2)〉45|-〉3|+〉6+

|φ(b1,b2⊕1)〉12|φ(c1,c2⊕1)〉45|-〉3|-〉6).(72)

Bob用Bell基测量粒子1和2,如果他的测量结果是|φ(b1,b2)〉或|φ(b1,b2⊕1)〉,那么控制者的粒子相应地塌缩为|+〉3或|-〉3.没有控制者的信息,Bob能够得到比特b1,但不能得到比特b2,同样,没有控制者的信息,Charlie能够得到比特c1,但不能得到比特c2,因此,需要在控制方的帮助下Bob和Charlie才能获得经典信息.

5) 控制者用{|+〉,|-〉}测量粒子3和粒子6,Bob和Charlie的量子比特塌缩成

|φ(b1,b2⊕m1)〉12|φ(c1,c2⊕m2)〉45, (73)

如果粒子3的测量结果是|+〉,则m1=0,否则m1=1.如果粒子6的测量结果是|+〉,则m2=0,否则m2=1.在获得m1的值之后,通过做Bell基测量,Bob能得到比特b1和b2.同理在获得m2的值之后,通过做Bell基测量,Charlie能得到比特c1和c2.步骤1与原始密集编码的编码步骤相似,在步骤2,Alice锁住2个GHZ态纠缠的信道.步骤3与原始密集编码方案发送粒子步骤类似.在这3个步骤之后,由于所有量子比特仍然是纠缠的,因此Bob和Charlie不能单独获得信息,系统粒子1和2的约化密度矩阵以及系统粒子3和4的约化密度矩阵都是I/4,因此,Bob和Charlie都不能从自己的系统获得编码的信息,除非他们合作.在步骤4,Bob和Charlie一起合作解纠缠信道.在步骤5,在得到控制者的允许之后,Bob和Charlie就能获得他们期望得到的信息.

6 结束语

自Bennett等[1]提出量子密集编码以后,作为量子信息理论的重要分支之一,量子密集编码引起了学者的广泛关注,目前已经有很多理论和实验的方案.作为量子密集编码的推广,受控密集编码与同时密集编码已成为编码领域的研究热点.在Bennett密集编码的基础上增加1个控制方的参与,进而滋生了受控密集编码方案的设计想法.同时密集编码是在密集编码的基础上,提出以2个纠缠的EPR对作为量子信道,1个发送者多个接收者的编码方案.本文主要综述量子密集编码在量子信息领域的研究现状,首先介绍原始量子密集编码和受控密集编码的相关协议.接着介绍同时密集编码和受控同时密集编码的一些方案.就目前而言,虽然在量子密集编码方面已经有了大量的研究,但对于同时密集编码的研究较少,同时密集编码还是1个新的研究课题,还有很多问题值得深入研究和探讨,如:1) 在控制者的监督下,如何进行双向经典信息的传递(即双向受控密集编码)?2) 如何以部分纠缠态作为通信信道设计同时密集编码协议?3) 在受控同时密集编码协议中,如何度量控制者的控制力?

总之,量子密集编码作为量子纠缠的重要应用之一,依然有待进一步研究和推广.