一种考虑截面任意变形模式梁的有限元模型

何欢，宋大鹏，张晨凯, 2，陈国平, 2

1.南京航空航天大学 机械结构力学及控制国家重点实验室,南京 210016 2. 南京航空航天大学 振动工程研究所,南京 210016

机翼作为飞机的重要承力部件，对飞机的飞行性能有着重要的影响[1]。在结构设计与强度分析阶段，对机翼进行有限元建模及分析是不可或缺的一步。目前机翼最为常见的建模方法是将机翼简化为“杆板组合结构”[2]，但该建模方法工作量较大，用于静力学分析尚可，动力学分析时就会显得计算量过大。在机翼结构初级设计以及结构优化阶段，机翼各构件的参数会不断调整变化，采用“杆板组合结构”建模方法就会显得较为繁杂，效率不高[3]。为了避免分析过于复杂，特别是在动力学分析中，只需要能够反映结构总体性能的简化模型即可，因而需要寻求一种更为简化的模型。

建立等效有限元模型是解决上述问题的一种途径，如等效梁模型[4-6]和等效板模型[7-9]。然而，等效有限元模型的建立需要结合工程经验，而且精度也受到一定的限制。此外，同时考虑静力与动力学分析的等效有限元模型缺乏全面的研究[10]。因此为了简单、有效地进行结构特性分析，建模时尽可能减少结构自由度，建立更加简洁的模型以及分析方法就显得很有必要。考虑到机翼以及机翼各主要部件(蒙皮、长桁、翼梁等)通常都是细长结构的特点，如果能够建立一种梁模型，使得机翼中各细长部件均采用一维梁单元进行建模，那么模型将十分简洁，结构自由度也将大大降低，进而给机翼的有限元建模与分析带来便利。

目前最为常见的梁模型有Euler-Bernoulli梁模型和Timoshenko梁模型。Euler-Bernoulli梁忽略了横向剪力和横向正应变的影响，适用于剪切变形影响较小的细长梁[11]，Timoshenko梁假设剪应变在给定横截面上为常值，而切应力却不是常数，与弹性力学不符。对于高跨比较大的深梁而言，其切应力沿截面变化也不再满足一阶剪切变形理论，故Timoshenko梁理论也不再适用[12-16]。在一些工程分析中，如机翼等在复杂载荷作用下，高阶剪切变形、翘曲变形较大，而上述梁理论均无法反映截面面内变形，因此存在计算精度不足的问题。在一些商用软件中如需考虑高阶剪切变形的影响，或者处理复杂截面形状结构时，则推荐使用实体单元，而实体单元建模又会带来结构自由度大幅增加、效率偏低的问题。

为此，本文引入若干个截面特征点，以截面特征点位移作为未知量，引入拉格朗日插值函数对梁轴向坐标上的任意截面上的特征点的位移进行插值，描述梁截面的复杂变形模式，建立一种可用于任意截面梁的有限元模型，结合虚功原理推导了截面插值梁单元的刚度矩阵和质量矩阵。最后，利用截面插值梁模型对机翼各部件进行建模，并展开典型工况下的静力学分析以及动力学分析(模态分析、颤振分析、动响应分析)，通过与Nastran实体单元计算结果对比验证该模型的可靠性。

1 构造梁位移场

1.1 拉格朗日插值多项式介绍

二元拉格朗日插值多项式一个重要的特点是其在自身点处值等于1，而在其他点处值等于0，且所有插值函数之和恒为1[17]。根据插值点数选择的不同，可以得到不同精度的插值函数，与有限元理论中的二维拉格朗日单元插值函数相同。三点插值(L3)、四点插值(L4)和九点插值(L9)的拉格朗日多项式分别对应于传统有限元中三节点三角形单元、四节点四边形单元和九节点四边形单元的形函数。图1所示为局部坐标系ξ-η平面上的标准拉格朗日单元。

对三角形单元可以直接利用广义拉格朗日插值函数法(划线法)构造其插值函数，而构造拉格朗日矩形单元插值函数的一个简便而系统的方法是通过2个坐标方向适当方次的拉格朗日多项式的乘积得到[18]。图1中3种单元对应的拉格朗日多项式为[19]

L3:F1=1-ξ-η,F2=ξ,F3=η

(1)

k=1,2,3,4

(2)

L9:

(3)

式中：ξk和ηk为特征点k的坐标。

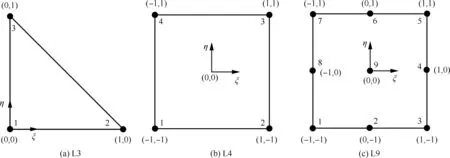
图1 拉格朗日单元Fig.1 Lagrange element

1.2 梁位移场

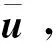
k=1,2,…,m

(4)

(5)

式中:uxk、uyk和uzk(k=1,2,3,4)为截面特征点3个方向上的位移分量。

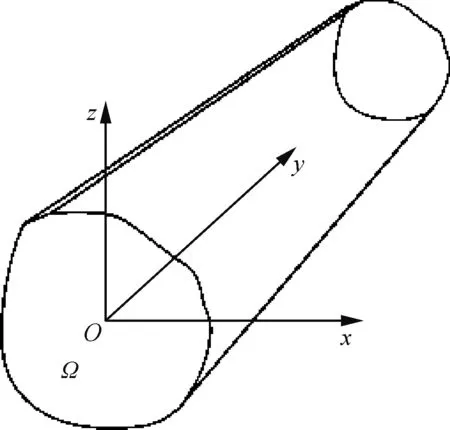
图2 截面插值梁示意图Fig.2 Cross-section interpolation beam diagram

2 截面插值梁的有限元模型

2.1 梁单元位移函数

n节点梁单元截面特征点位移向量可表示为

(6)

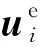
(7)

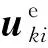
(8)

2.2 应变和应力

将式(7)代入几何方程和物理方程，可得单元应变矩阵和应力矩阵分别为

(9)

k=1,2,…,m;i=1,2,…,n

(10)

式中：L为微分算子矩阵，D弹性矩阵，考虑各向同性材料，其分别为

(11)

(12)

其中：

其中：E为弹性模量；υ为泊松比。

2.3 单元刚度矩阵与质量矩阵

假定单元发生虚位移，根据式(7)和式(9)有

(13)

(14)

式中：l为截面特征点数；j为节点号。

若材料密度为ρ，根据达朗贝尔原理，单元内单位体积分布惯性力为

(15)

在外力中考虑惯性力，则虚功原理可写为

(16)

将式(10)、式(13)和式(14)代入整理可得式(16) 中各项分别为

(17)

(18)

(19)

式中：Pv和Ps分别为作用在单元上的体积力和面力；Pp为集中力。

式(16)进一步整理可得

(20)

(21)

令

(22)

则式(21)可整理为

(23)

可得

(24)

式中：下标组合lj代表着梁第j个节点所在平面的第l个插值点。

2.4 梁单元截面的离散与组集

对于复杂形状截面梁单元，可以通过将横截面细分为几个拉格朗日单元的方法进行有限元分析。由于位移函数中未知量为各插值点位移，所以单元叠加时只需叠加相应插值点即可，如图3所示。

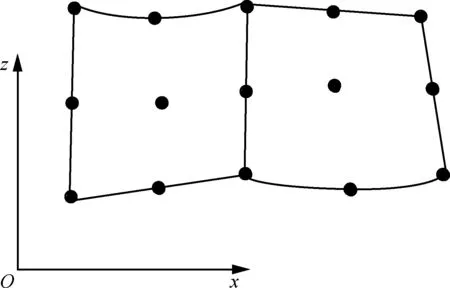
图3 单元截面叠加Fig.3 Superimposed cross-section element

3 算例1

考虑图4所示矩形截面梁，梁长L=2 m，截面形状为正方形，横截面尺寸为a=0.1 m。弹性模量E=75 GPa，泊松比υ=0.33，材料密度为ρ=2 700 kg/m3。在梁自由端作用竖向集中力P=2 000 N，作用部位如图4所示。

采用截面插值梁单元(L9)对梁结构进行分析，单元节点数取4，同时利用实体单元进行建模作为对比，实体单元建模时在每一个特征点处设节点以保证2种模型有着相同的自由度。

图5给出了随梁单元数变化时2种模型自由端挠度uz的计算结果。从图中可以看出，虽然实体单元模型和插值梁单元模型都对截面面内进行了离散，但是当轴向网格数较少时，实体单元模型轴向尺寸将明显大于其他2个方向尺寸，单元刚度矩阵的雅可比行列式远小于1，使得单元刚度矩阵中表征不同方向的刚度系数相差过大，降低了挠度计算精度。而本文方法只要轴向划分的单元数足够描述梁的挠曲线特征即可达到满意的计算精度。从图5中可以看出，当截面插值梁单元模型的单元数为5时，挠度计算结果即可收敛，而实体单元模型则需要远多于梁单元模型自由度时才能达到相同的收敛结果，因此截面插值梁单元在处理细长结构时相比实体单元优势明显。

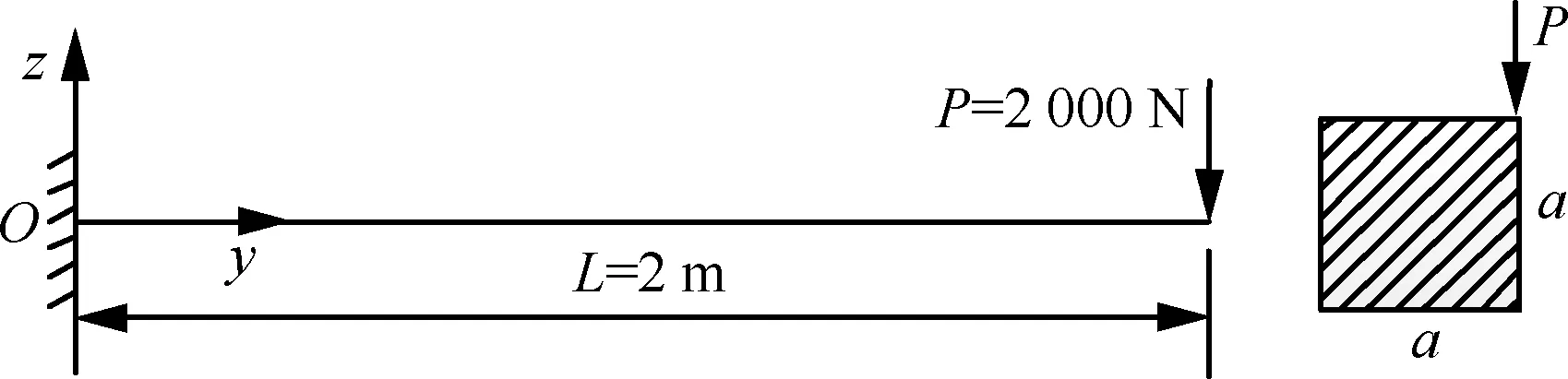
图4 悬臂梁示意图Fig.4 Diagram of cantilever

图5 挠度随轴向单元数变化曲线Fig.5 Curves of variation of deflection with element number along axis

4 算例2

考虑图6所示一端固支工字截面梁，其中W=100 mm，H=100 mm，t1=8 mm，t2=5 mm，长度L=1 000 mm。弹性模量E=210 GPa，泊松比υ=0.29。在自由端作用如图6所示的一组集中力，大小为2 000 N。

根据Euler-Bernoulli梁以及Timoshenko梁理论，这些力自相平衡，截面不会发生变形，而在实际中很容易想象出，截面会发生明显变形。截面插值梁模型可以完整描述这种变形，自由端截面变形如图7所示。图中7L9和14L9分别表示采用了7个和14个截面插值梁单元，从结果中也可以看出，通过增加截面面内的单元数可以有效提高模型的精度。

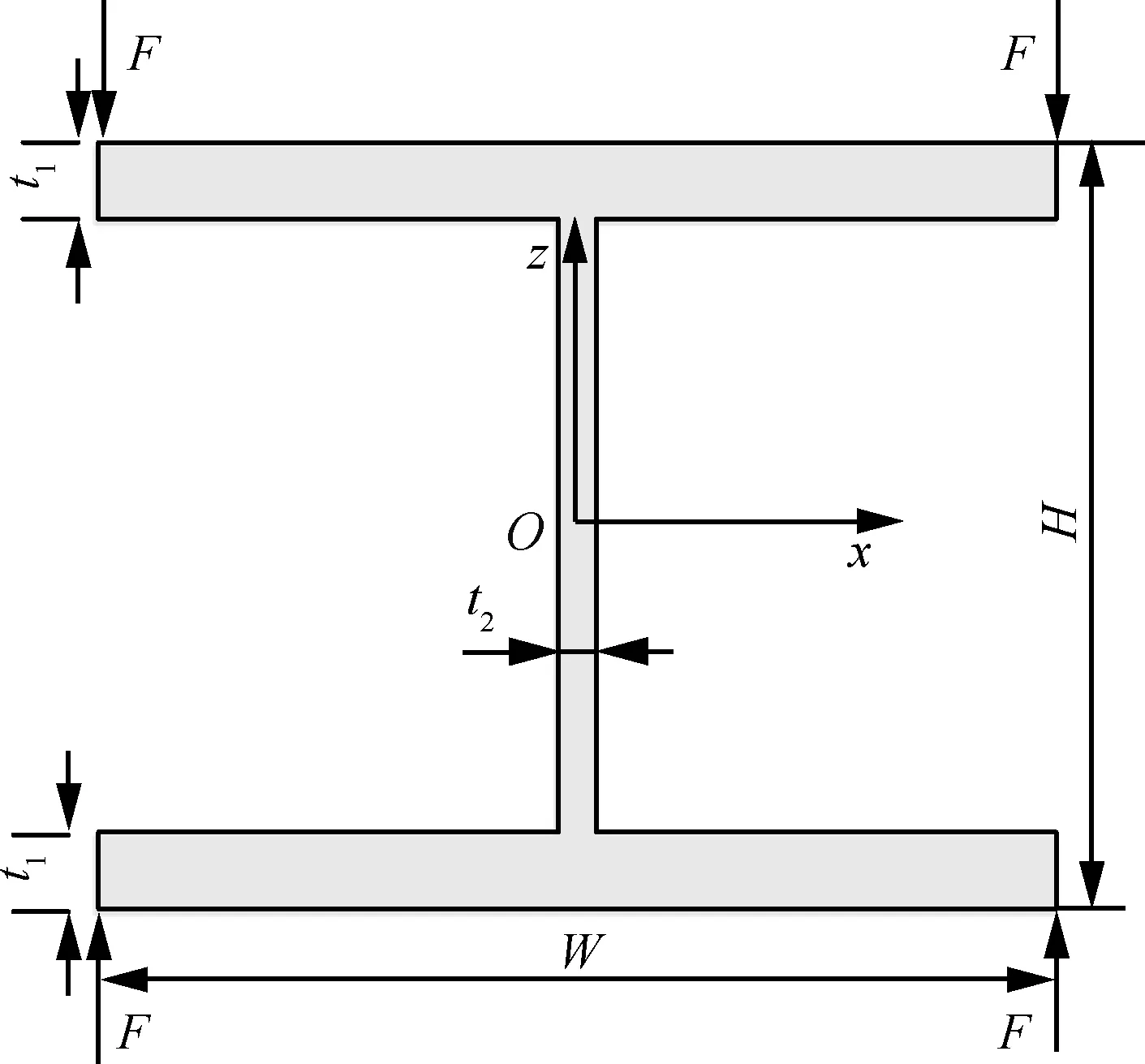
图6 工字梁截面示意图Fig.6 I-shaped beam profile diagram

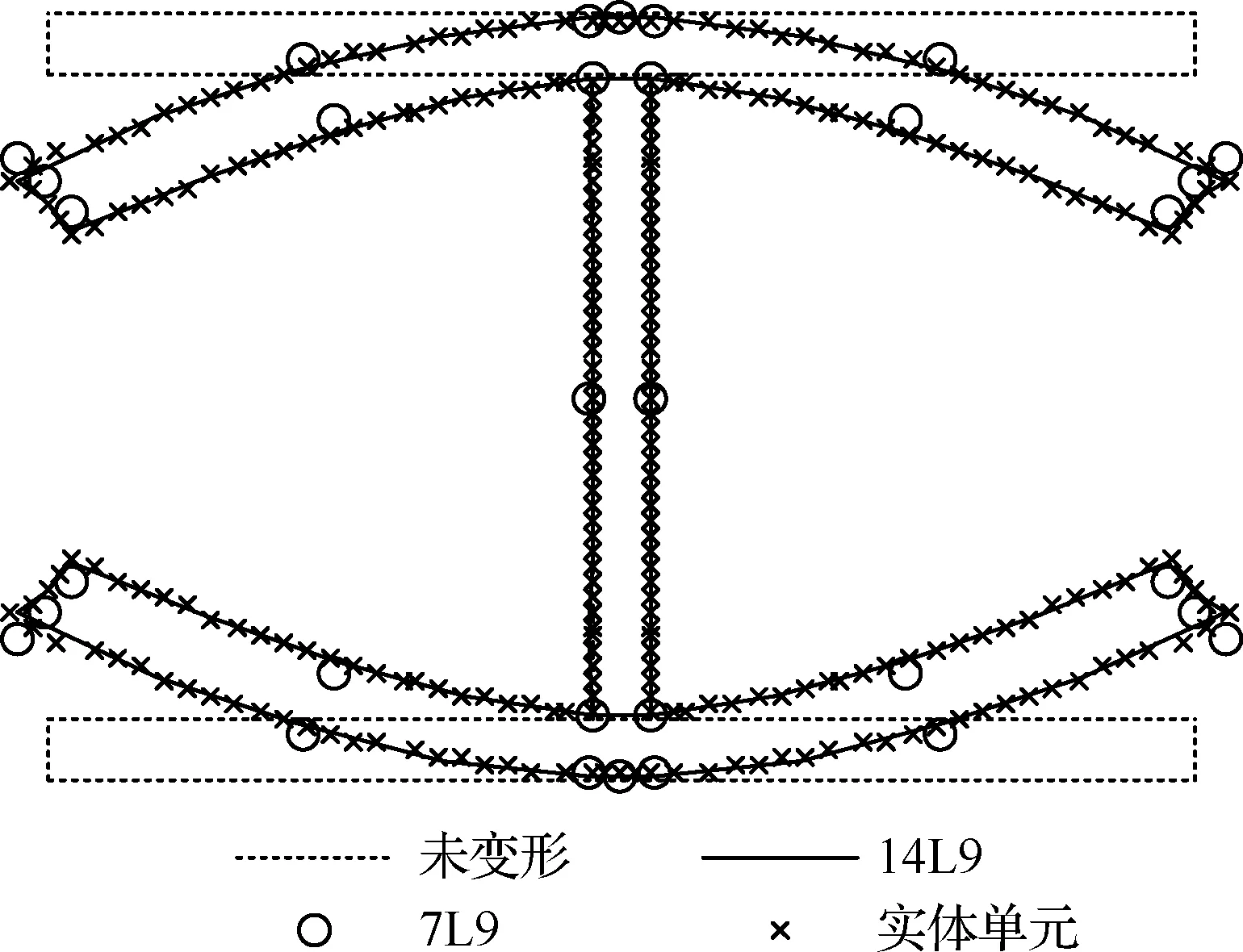
图7 截面变形Fig.7 Cross-section deformation

5 算例3

考虑图8所示直机翼结构，机翼展长l=6 m，翼型为NACA2415，弦长c=1 m，蒙皮厚度为3 mm， 翼梁厚度为5 mm，其余具体尺寸如图8所示。为方便分析，机翼各部件采用相同铝合金材料，弹性模量E=75 GPa，泊松比υ=0.33，材料密度为ρ=2 700 kg/m3。

5.1 静力学分析

采用截面插值梁单元对机翼各部件进行建模分析，并分别与经典梁单元以及Nastran实体单元计算结果进行对比分析。截面插值点如图9所示，截面通过图示方法离散与组集，机翼展向单元数取8。经典梁单元考虑Euler-Bernolli梁以及Timoshenko梁2种梁单元，机翼梁模型的各形状属性数据借助Patran软件得到。同时为得到机翼结构复杂应力分布情况，对机翼结构全部采用实体单元建模(如图10所示)作为验证标准。实体模型中共有125 160个单元，其中124 140个Hex8单元，1 020个Wedge6单元，总节点数为169 290。

机翼坐标系及本文计算输出点如图11所示。

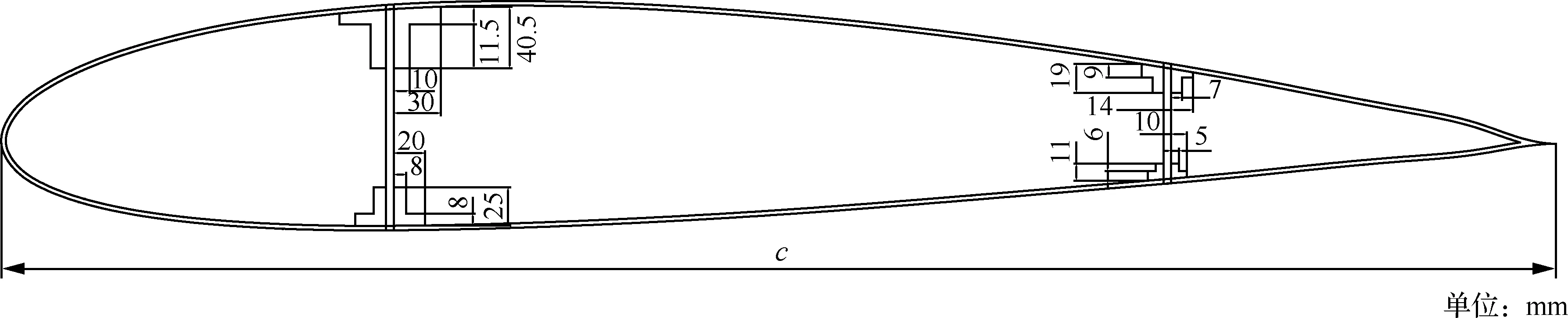
图8 机翼截面及尺寸Fig.8 Size and shape of wing cross-section

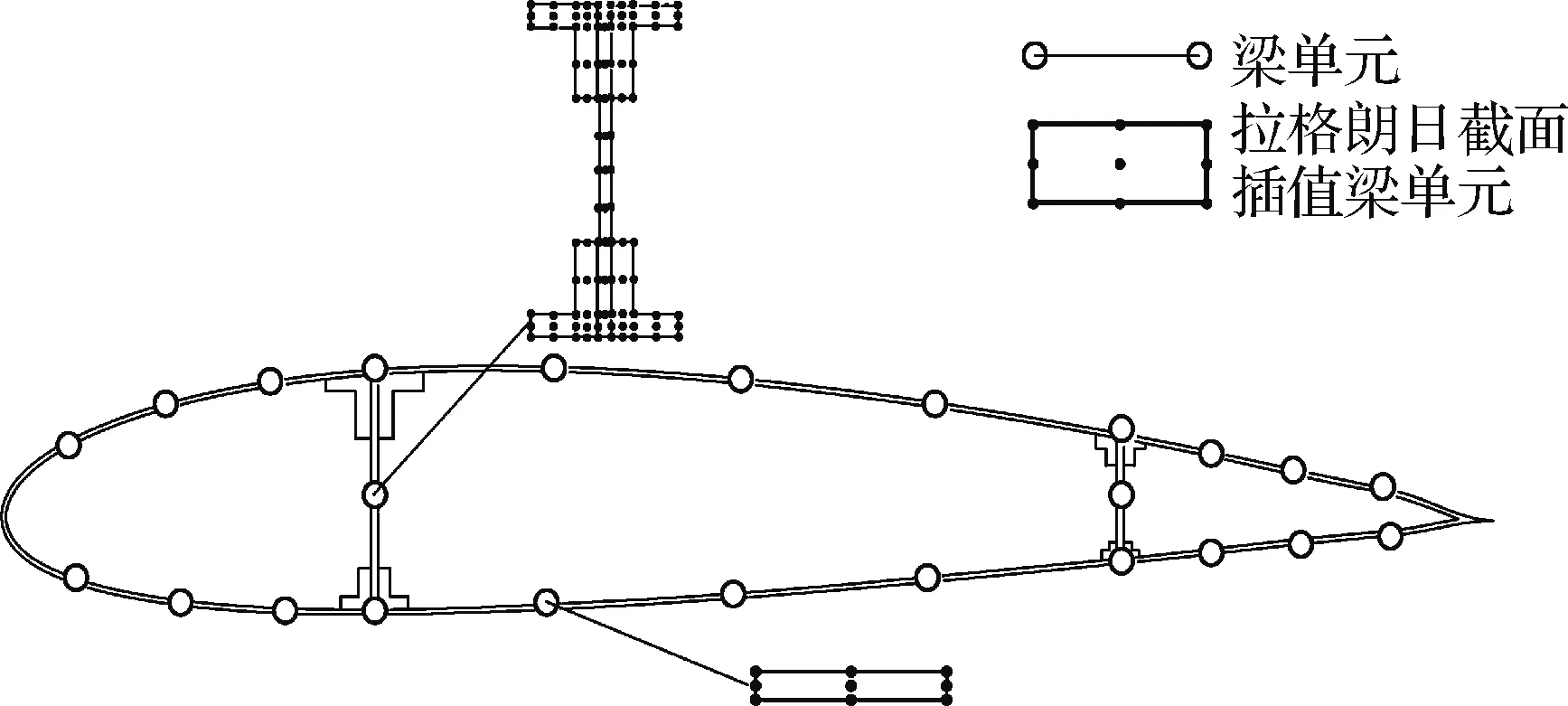
图9 机翼截面插点值示意图Fig.9 Interpolation points of wing cross-section diagram

图10 Patran实体单元模型Fig.10 Solid element model of Patran

图11 机翼坐标系Fig.11 Coordinate system of wing

兼顾机翼实际受载情况(惯性载荷、局部质量)以及简化分析(集中载荷)的需要，针对表1所示工况条件展开分析，其中集中力及局部质量点均位于点4、y=4 m处，g取9.8 m/s2，惯性力方向为z方向。

本文采用73个L9单元模拟整片机翼。表2给出了2种工况条件下部分特征点的位移以及应力值，并对截面插值梁模型、经典梁模型计算结果与有限元软件Nastran实体单元计算结果进行了对比，其中EBBM表示Euler-Bernolli梁模型，TBM表示Timoshenko梁模型。表2中同时给出了各种模型自由度对比情况。

表1 工况表Table 1 Condition sheet

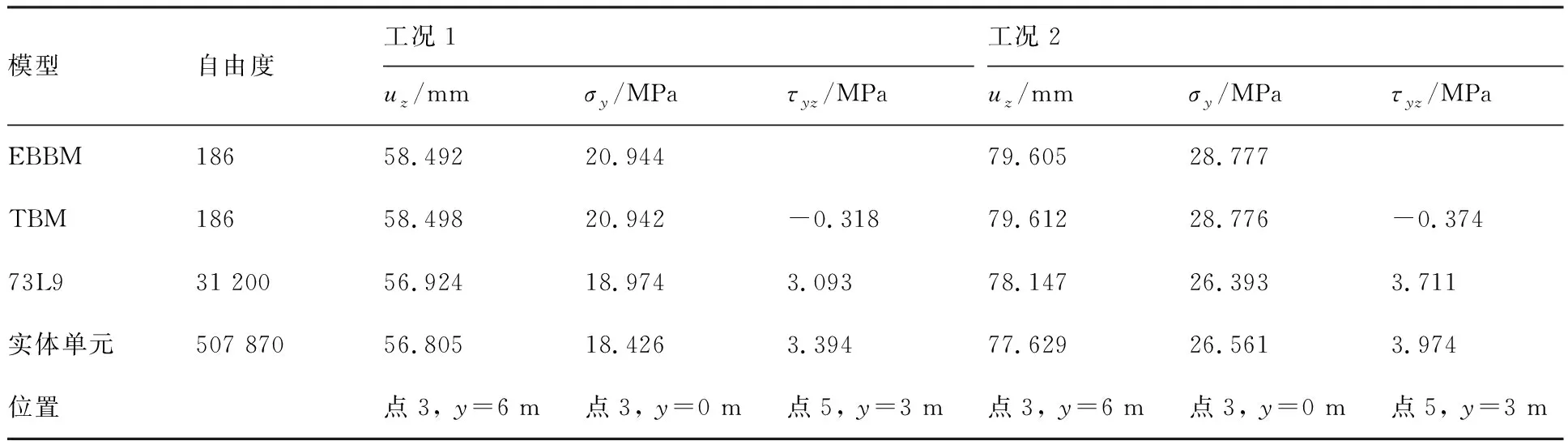
表2 部分位移及应力结果Table 2 Partial displacement and stress results

图12为机翼自由端截面变形图。从表2及图12可以看出，相比经典梁单元，截面插值梁单元计算结果与实体单元计算结果更为接近，但差异很小。从自由度对比情况可以看出，截面插值梁模型自由度远小于实体模型自由度，因而有着更高的计算效率。

图13为点1、点2、点3及点4所在轴线正应力沿轴线y分布曲线图，从图中可以看出，截面插值梁单元计算结果精度整体高于经典梁单元，尤其是图13(d)中，在点4载荷作用部位正应力变化趋势突变，截面插值梁模型可以准确反映出这种变化，与实体单元模型一致。

图14为点5处剪应力分布曲线，其中图14(a)为沿轴线方向剪应力分布图，图14(b)为截面y=3 m 处沿z方向剪应力分布图，从图中可以看出，截面插值梁模型剪应力计算结果与实体模型结果基本一致。图15为点6处剪应力分布图，图15(a)为沿轴线方向剪应力分布图，图15(b)为截面y=3 m处沿z方向剪应力分布。

综合以上2种工况的静力分析结果来看，虽然经典梁单元可以得到部分点的位移分析结果，部分点的正应力分析结果误差也不大，但其无法得到结构的剪应力分布结果，而截面插值梁单元可以得到完整的静力分析结果，且均有着堪比实体单元模型的计算精度，模型自由度也远小于实体模型，因而基于截面插值梁的机翼模型在静力学分析中有着独特的优势。

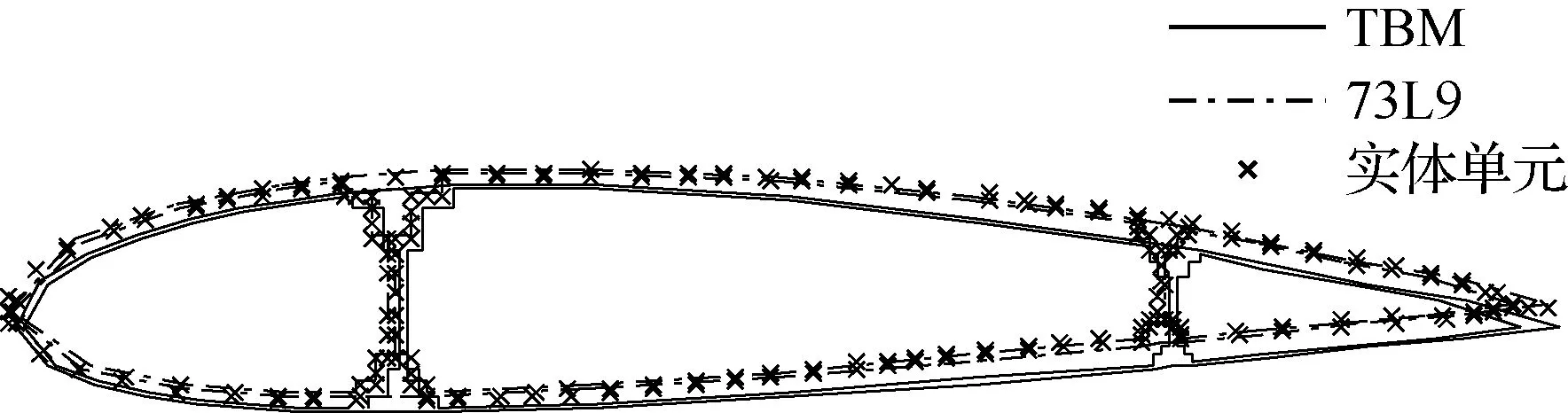
图12 机翼自由端截面变形图Fig.12 Deformation of wingtip corss-section

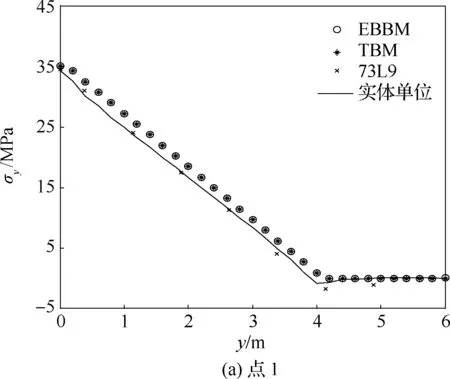
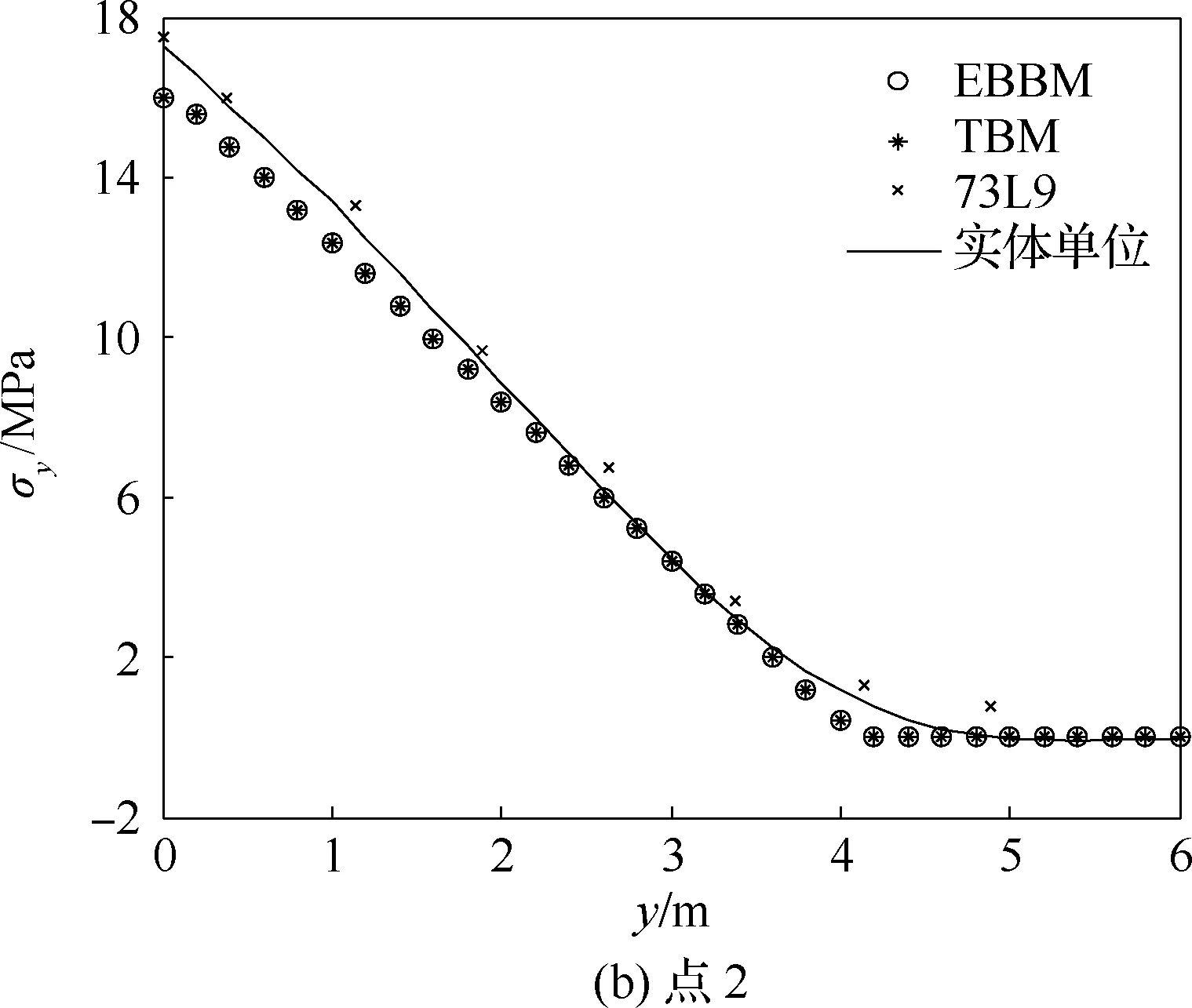
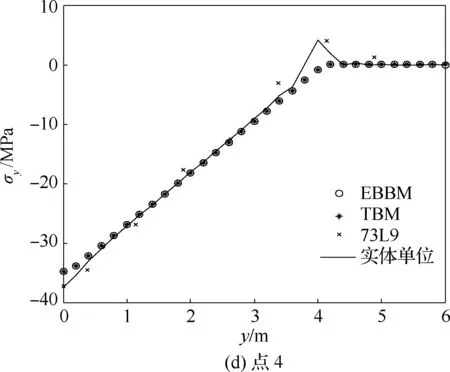
图13 正应力分布曲线(点1～4,工况1)Fig.13 Positive stress distribution curves (Points 1-4, Case 1)

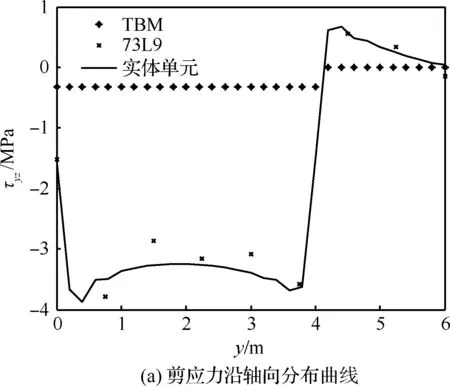
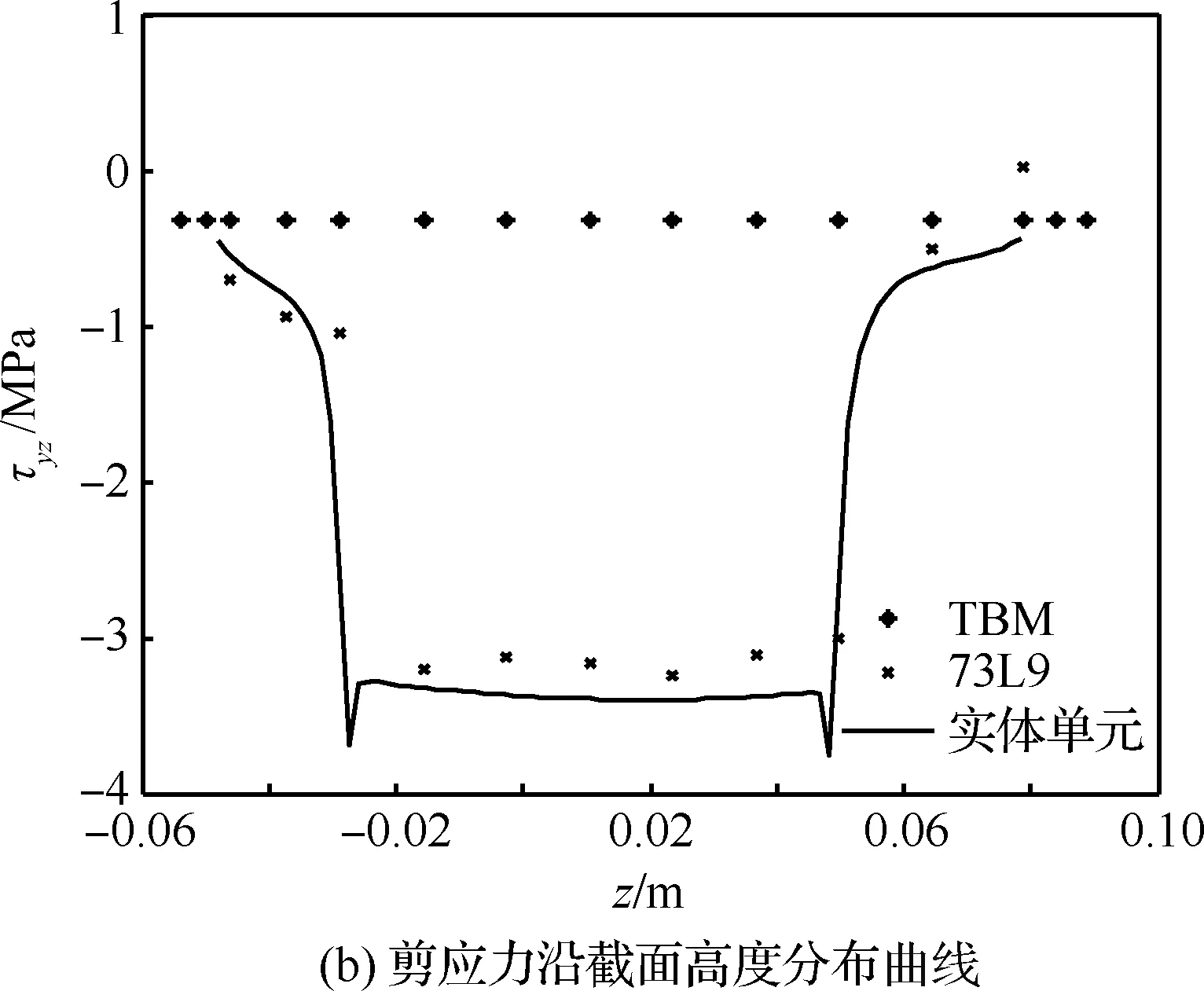
图14 剪应力分布曲线(点5，工况1)Fig.14 Shear stress distribution curves (Point 5, Case 1)

5.2 动力学分析

对机翼结构进行模态分析，分别考虑无集中质量和含有集中质量2种工况(如表1所示)。表3给出了几种不同机翼模型的前8阶固有频率。从表中可以看出，经典梁单元只能得到低阶弯曲模态，无法得到较高阶的扭转模态、弯扭耦合模态。图16给出了截面插值梁模型与实体模型振型结果对比图(不含集中质量)，图17为相应的MAC柱状图，对角线上前6阶模态置信度均大于0.95，前8阶大于0.90，说明采用本文方法的模型模态计算结果与精细化的实体单元机翼模态计算结果吻合程度很好。

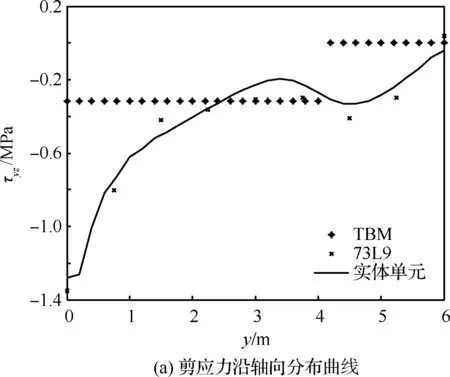
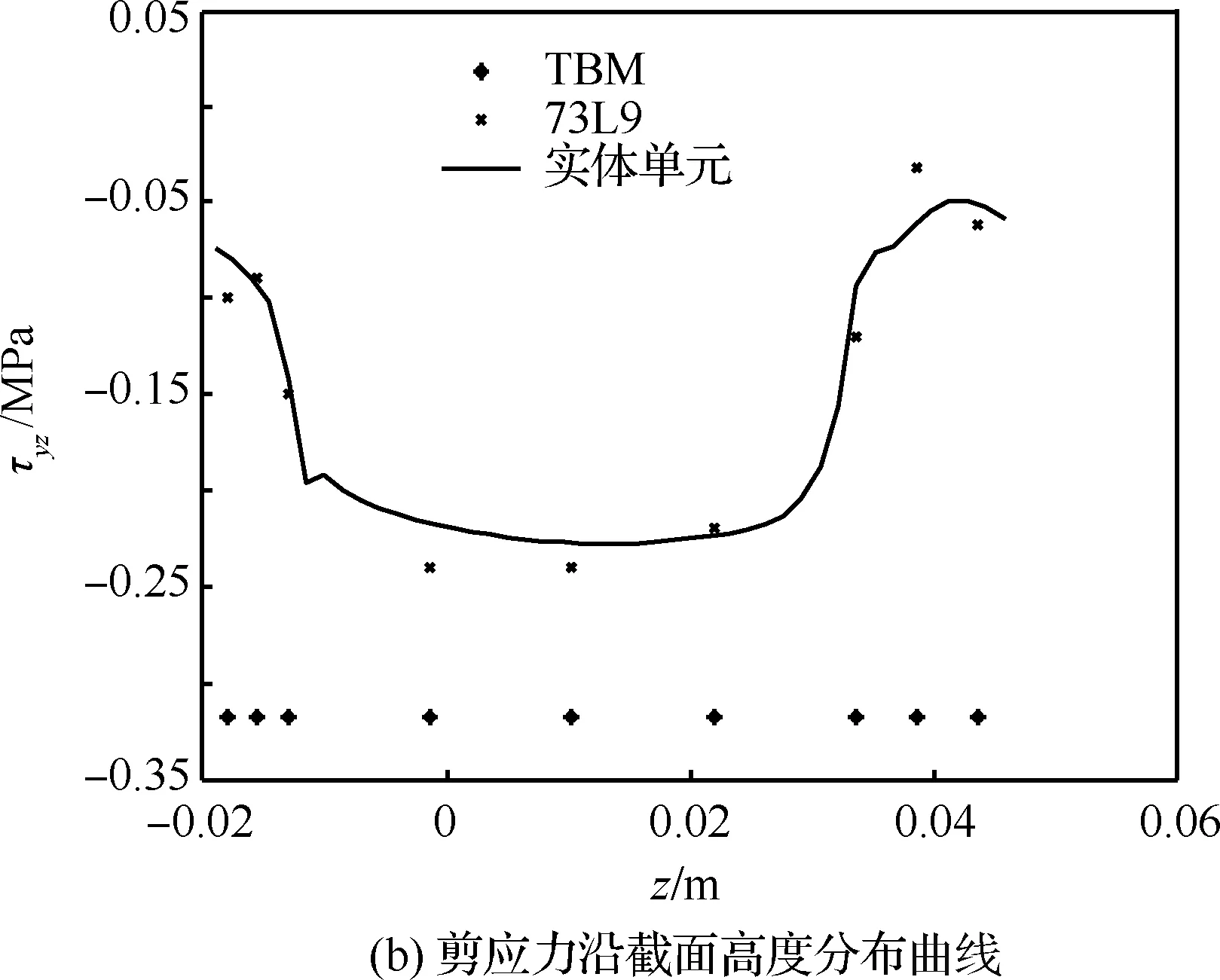
图15 剪应力分布曲线(点6，工况1)Fig.15 Shear stress distribution curves (Point 6, Case 1)

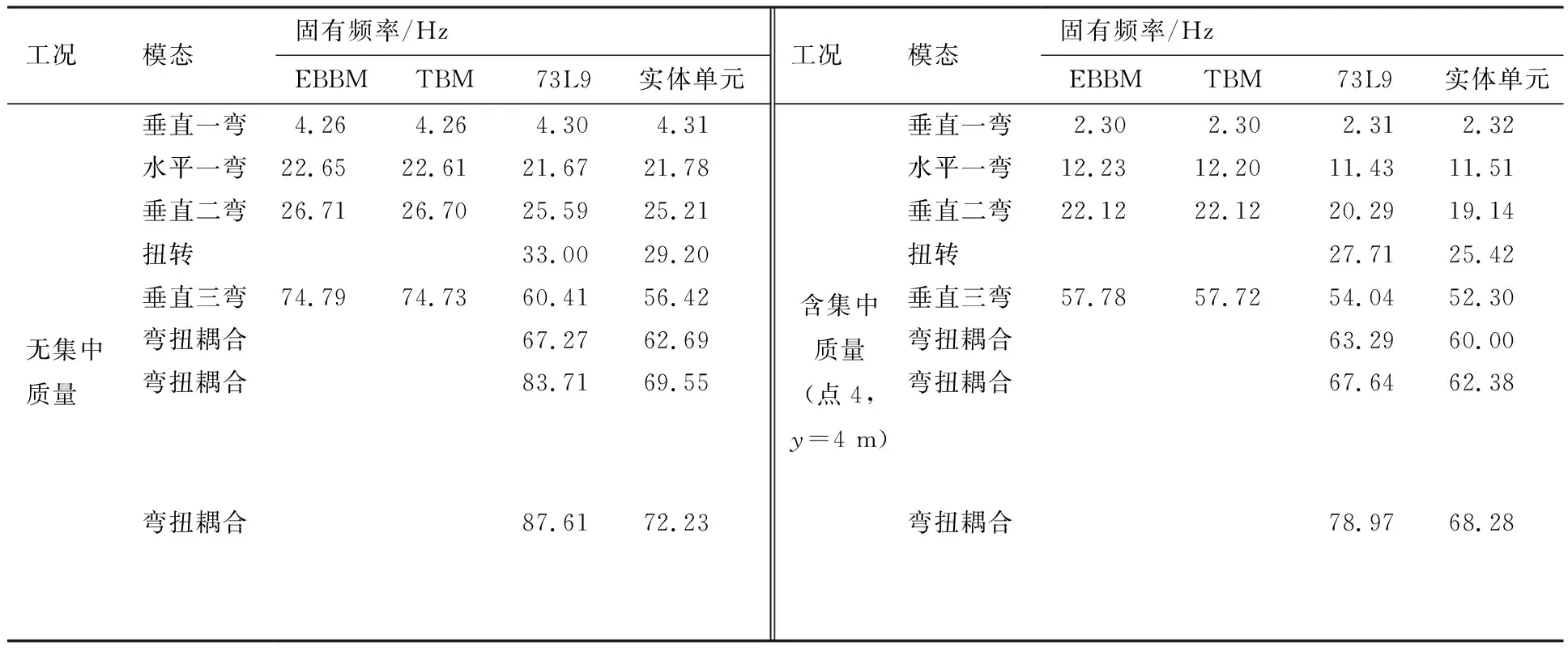
表3 固有频率计算结果Table 3 Natural frequency calculation results

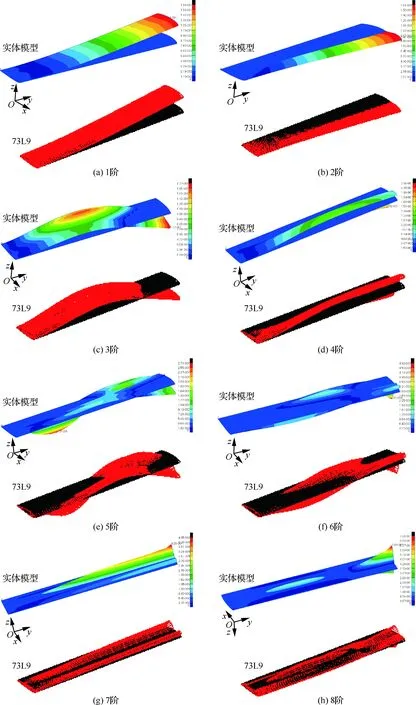
图16 振型结果对比Fig.16 Comparison of mode shapes

在模态分析的基础上，对该机翼展开颤振分析。为简化分析，在空气动力方面采用片条理论，直接利用二维流的已知结果计算气动力。在颤振初步估算阶段，对于大展弦比飞机，无集中质量的情况下可取机翼的一阶弯曲和扭转振型作为位移函数将机翼运动简化为2个自由度[20-21]。利用v-g法进行颤振分析，相应的v-g曲线和v-f曲线如图18所示。

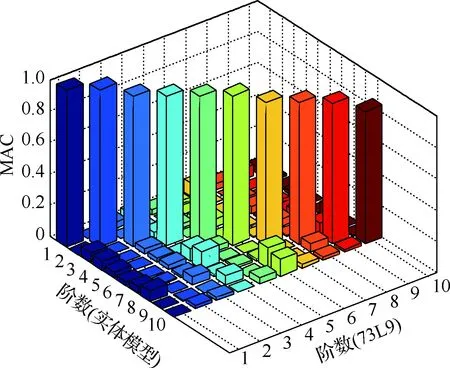
图17 MAC柱状图Fig.17 MAC histogram

图18 颤振计算结果Fig.18 Flutter calculation results

通过插值的方法得到g=0时对应的颤振速度和相应的颤振频率，表4中给出了2种模型的颤振特性对比结果。从计算结果可以看出，截面插值梁模型在颤振初步估算阶段可以得到较为满意的颤振计算结果。

为了进一步验证本文模型的有效性，对截面插值梁机翼模型展开时域响应分析。在点4、y=4 m 处沿z方向施加幅值为3 000 N、频率为20 Hz的正弦激励。分别采用振型叠加法和Newmark 法进行动响应计算，并与Nastran实体单元中的模态叠加和直接积分2种计算结果进行对比。部分点位移响应如图19和图20所示。

图19为振型叠加法计算结果对比，选取的模态数为10，从图中可以看出，2种模型计算结果基本一致，这也进一步验证了前述模态分析结果的可靠性。图20为直接积分法计算结果，从图中也可以看出，2种模型计算结果一致，基于截面插值梁的机翼模型可以很好地用于机翼结构的动响应分析。

表4 颤振计算结果Table 4 Flutter calculation results

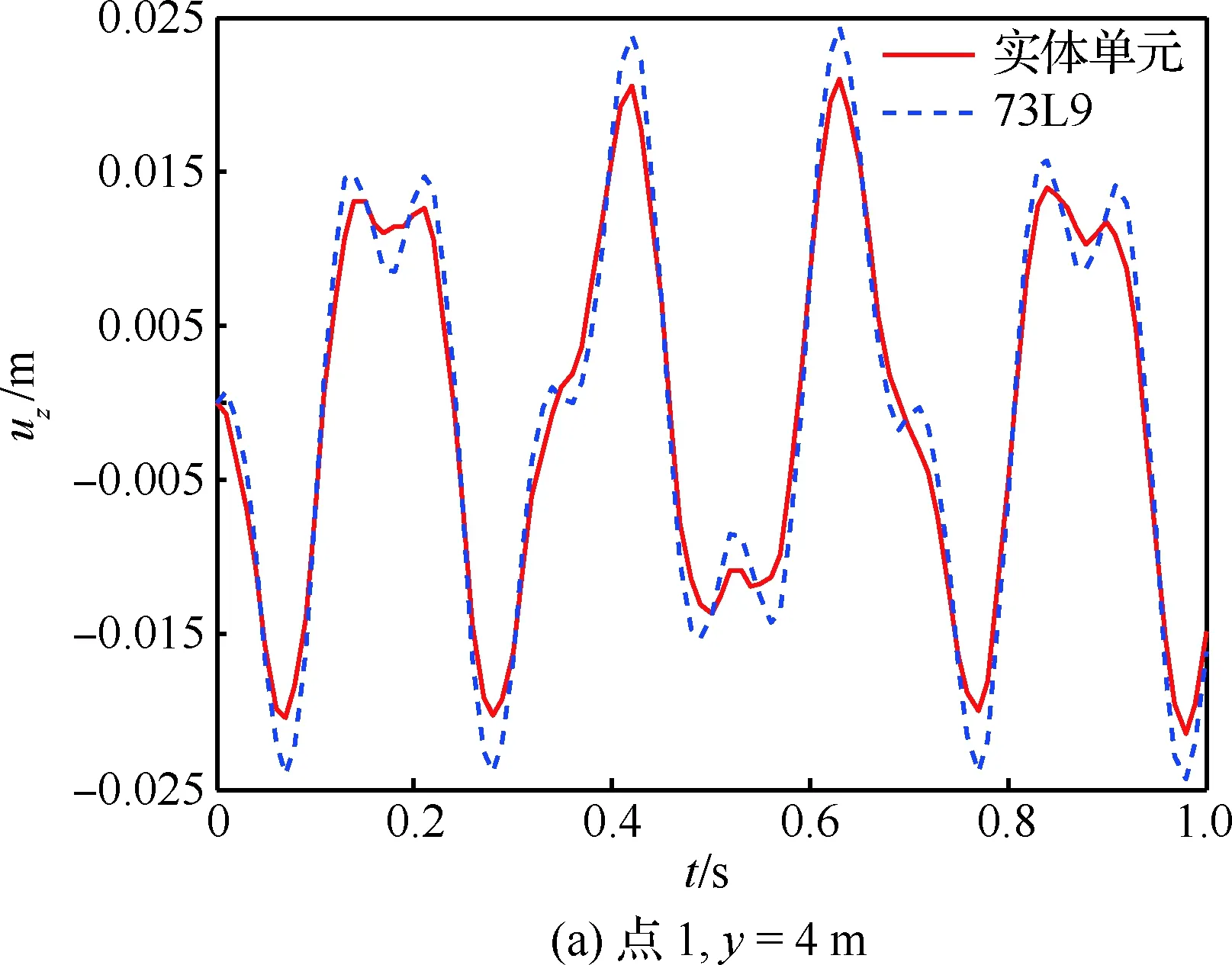
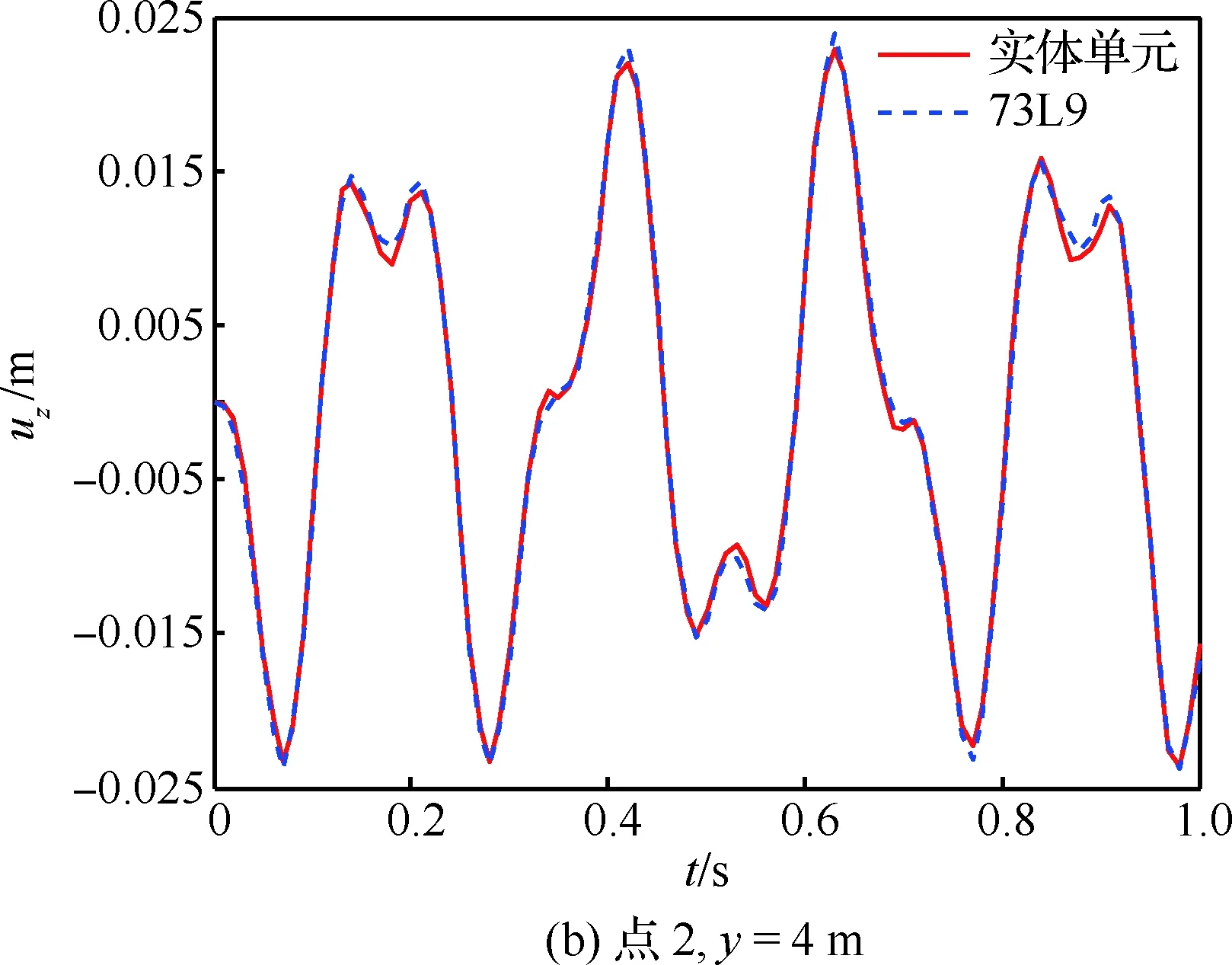
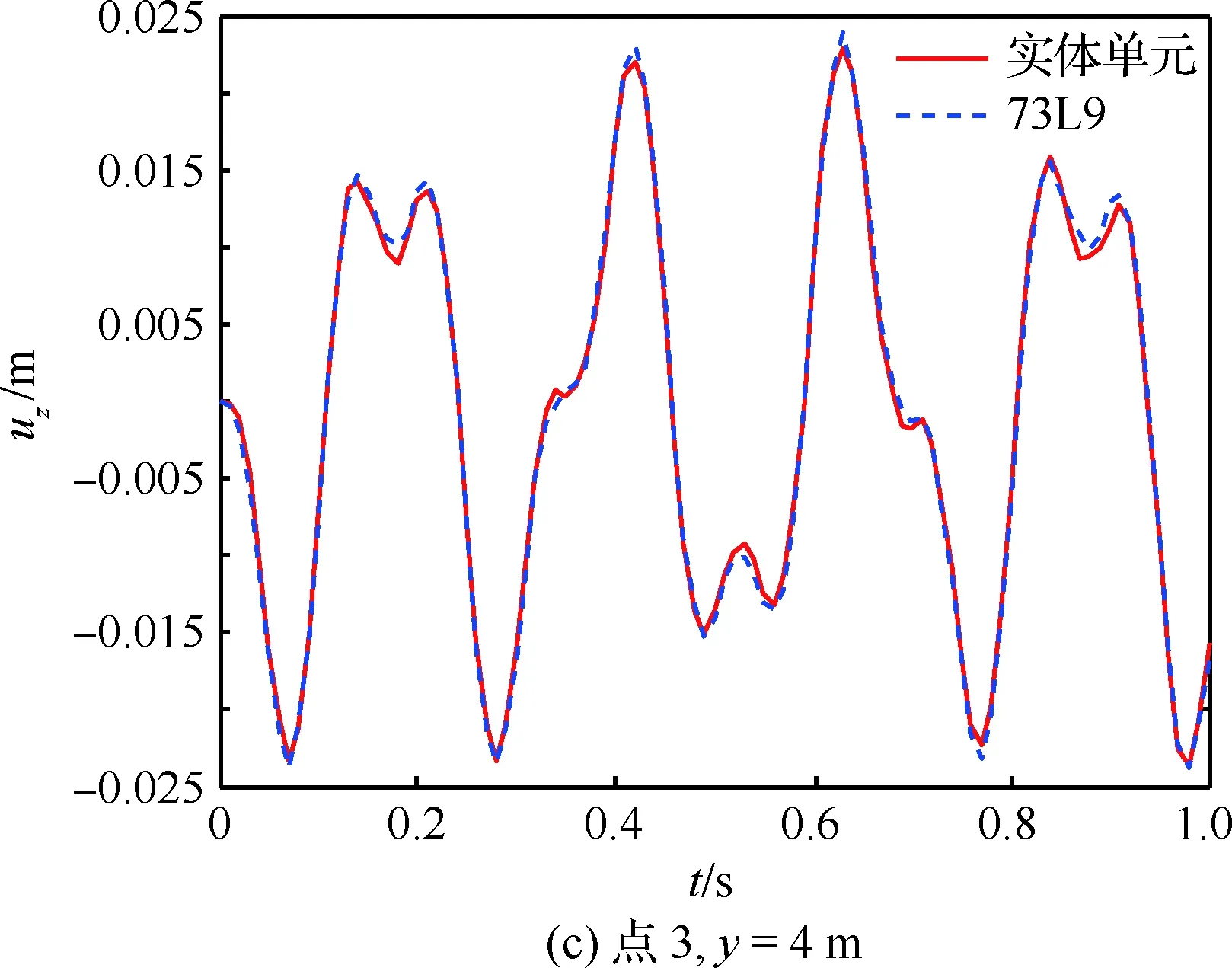
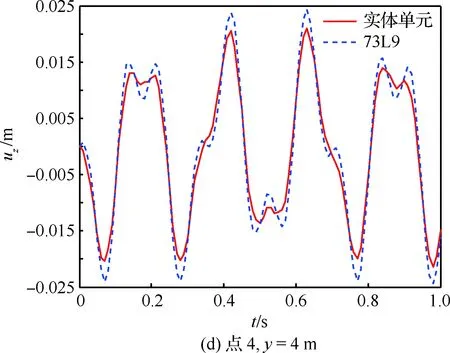
图19 位移响应图(振型叠加法)Fig.19 Displacement results (modal superposition method)

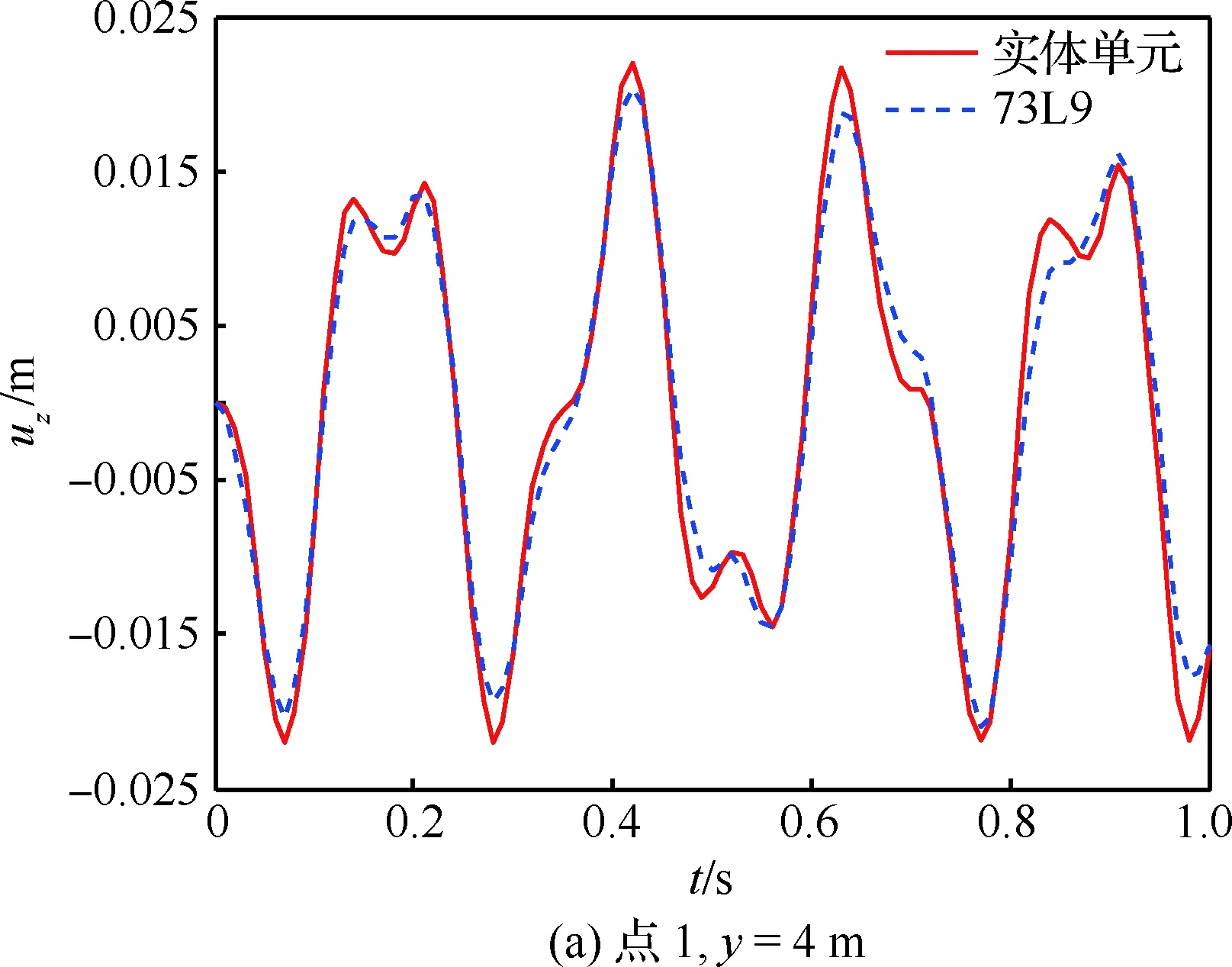
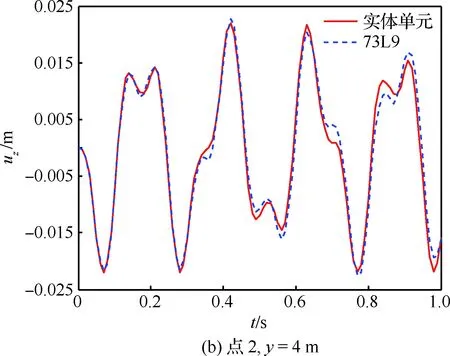
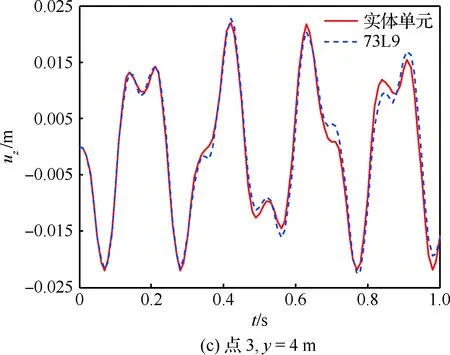
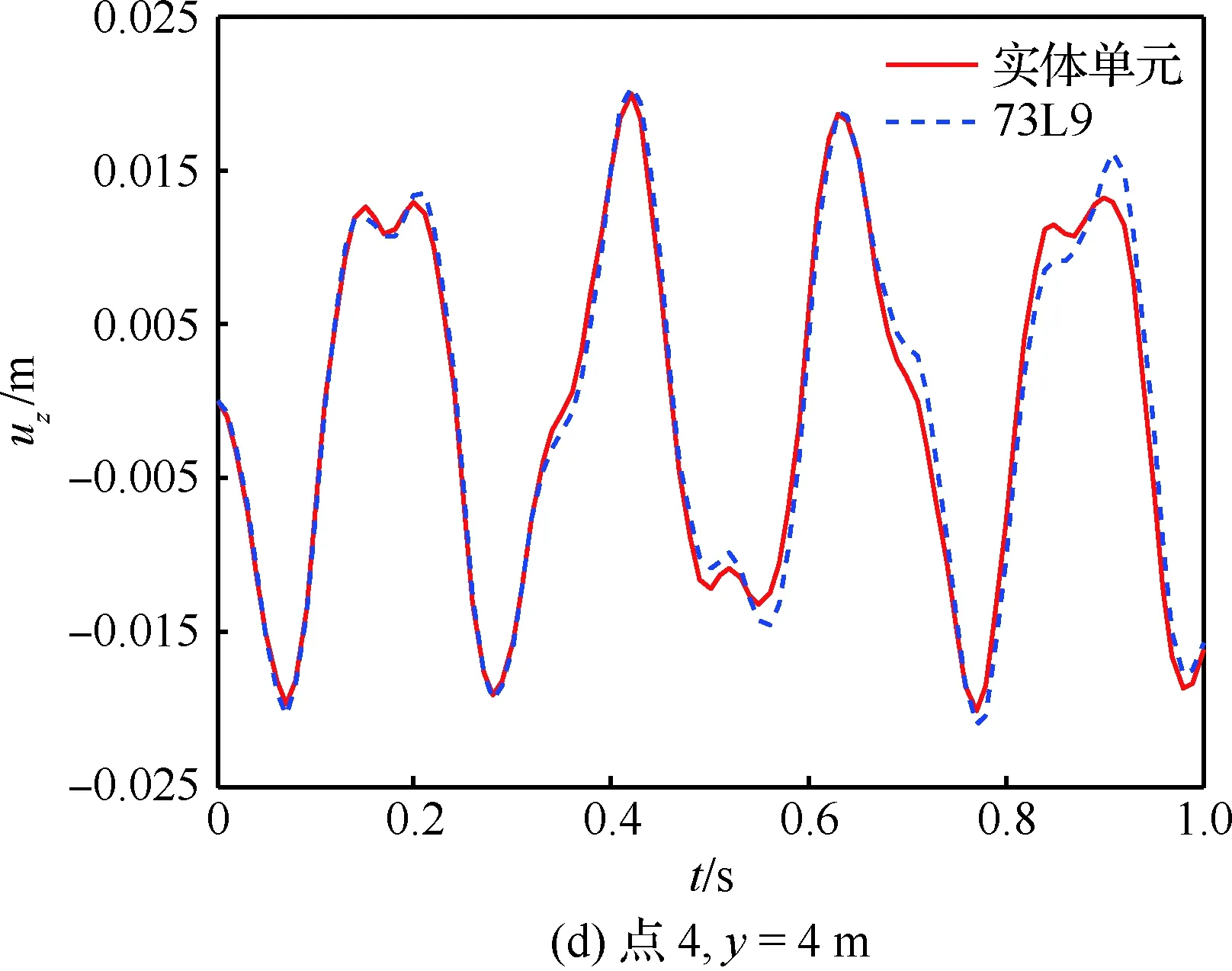
图20 位移响应图(直接积分法)Fig.20 Displacement results (direct integration method)

6 结 论

1) 截面插值梁单元通过截面特征点位移插值得到截面位移场，可以得到截面面内、面外完整截面变形。

2) 截面插值梁单元与经典梁单元相比，不仅有着更高的计算精度，还可以有效处理复杂截面形状细长结构；与实体单元相比，同等网格尺寸、同样误差等级下，截面插值梁单元模型自由度远远小于实体模型。

3) 截面插值梁单元可以用于简单机翼结构建模，并能够得到满意的静力学、动力学分析结果，为机翼的建模与分析提供了一种一维梁简化建模方法。