计及弹射滑车质量的某舰载无人机弹射动态响应分析

房兴波，聂宏, 2,*，张钊，魏小辉, 2，张明

1. 南京航空航天大学 飞行器先进设计技术国防重点学科实验室，南京 210016 2. 南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016

舰载机弹射起飞时，弹射滑车通过弹射杆与前起落架支柱连接，牵制杆通过锁定机构与前起落架防扭臂连接。弹射初始阶段，在飞机发动机推力的作用下，舰载机与牵制杆拉紧；弹射器启动后，牵制杆张紧力随着弹射力增加而增加，当牵制杆张紧力达到锁定机构的解锁阈值时，牵制杆与前起落架分离，弹射滑车拖拽舰载机前起落架向前滑行。

国外学者对舰载机弹射起飞过程做了大量研究工作：文献[1]阐述了前轮拖拽弹射的优点，并对E-2A飞机进行了弹射试验研究；文献[2]提出牵制杆解锁瞬间前起落架产生的振荡现象会给起落架结构带来严重的疲劳问题；文献[3]通过实验研究了A6-A飞机与航母的适配性；美国海军的舰载机弹射起飞技术发展比较早，关于舰载机前起落架结构[4]、牵制杆及解锁装置[5-6]以及飞机结构强度[7]已经形成了成熟的设计标准。

国内学者在舰载机弹射起飞领域的研究起步稍晚，但也做了相当多的研究工作。文献[8]采用智能代理模型方法建立了包含大气、海洋、舰船的舰载机弹射起飞模型；文献[9]分析了舰载机离舰姿态预设、导引律设计等相关问题，为离舰安全边界评估提供了依据；文献[10]研究了舰载机升降舵偏角对起落架突伸性能的影响，以及航母运动对舰载机离舰姿态的影响；文献[11]建立了蒸汽弹射器热力学模型，结合舰载机动力学模型分析了舰载机弹射过程，并与美军试验进行了对比。文献[12-13]分别从理论和试验出发，研究了舰载机前起落架弹射突伸性能。文献[14-15]研究了牵制杆载荷突卸瞬间前起落架结构振动问题，并提出了解决方法。文献[16]通过地面试验研究了舰载机弹射起飞牵制杆突卸瞬间弹射载荷通过前起落架传递至机身时的冲击响应。

目前已公开的文献中，舰载机弹射起飞动力学模型对弹射力的处理方法均为在弹射杆上直接施加弹射载荷，不考虑弹射滑车与起落架之间的耦合关系。但是在舰载机弹射过程中，弹射滑车与前起落架之间通过弹射杆连接，与前起落架形成耦合动力学系统。与舰载机起飞重量相比，尤其是对于舰载无人机而言，3 000 kg的蒸汽弹射器滑车质量已经不能忽略。

本文从弹射滑车与舰载机的耦合运动出发，建立了包含弹射滑车的舰载机拖拽弹射动力学模型，对某无人机拖拽弹射动态过程进行了计算，对比分析了弹射滑车质量对该无人机拖拽弹射过程动态响应的影响。

1 弹射滑车对弹射动态响应的影响机理

图1给出了弹射器弹射滑车组件的结构示意图，弹射滑车主要由弹射接头、导向架、导向轮等组成，并且与蒸汽活塞连接，美国海军C-13系列弹射器的弹射滑车质量高达3 000 kg。弹射滑车与舰载机起落架弹射杆相连，在弹射过程中组成一个耦合动力学系统。

舰载机弹射张紧状态下，由于发动机推力的作用，前起落架撑杆承受压缩载荷，牵制杆解锁后在弹射力的作用下前起落架撑杆载荷从压缩载荷突变成拉伸载荷[14]。载荷突变后，前起落架支柱在弹性撑杆的作用下会产生高频的纵向振动。由于前起落架撑杆和弹射杆几乎是在一条直线上，大质量的弹射滑车将使前起落架上的纵向振动更加剧烈。

前起落架上防扭臂与牵制杆连接，牵制杆解锁后，上防扭臂载荷也同时消失，前起落架缓冲器失去平衡，将带动机身做低频的垂向振动。由于弹射滑车与前起落架支柱连接，弹射滑车的质量将降低振动频率。

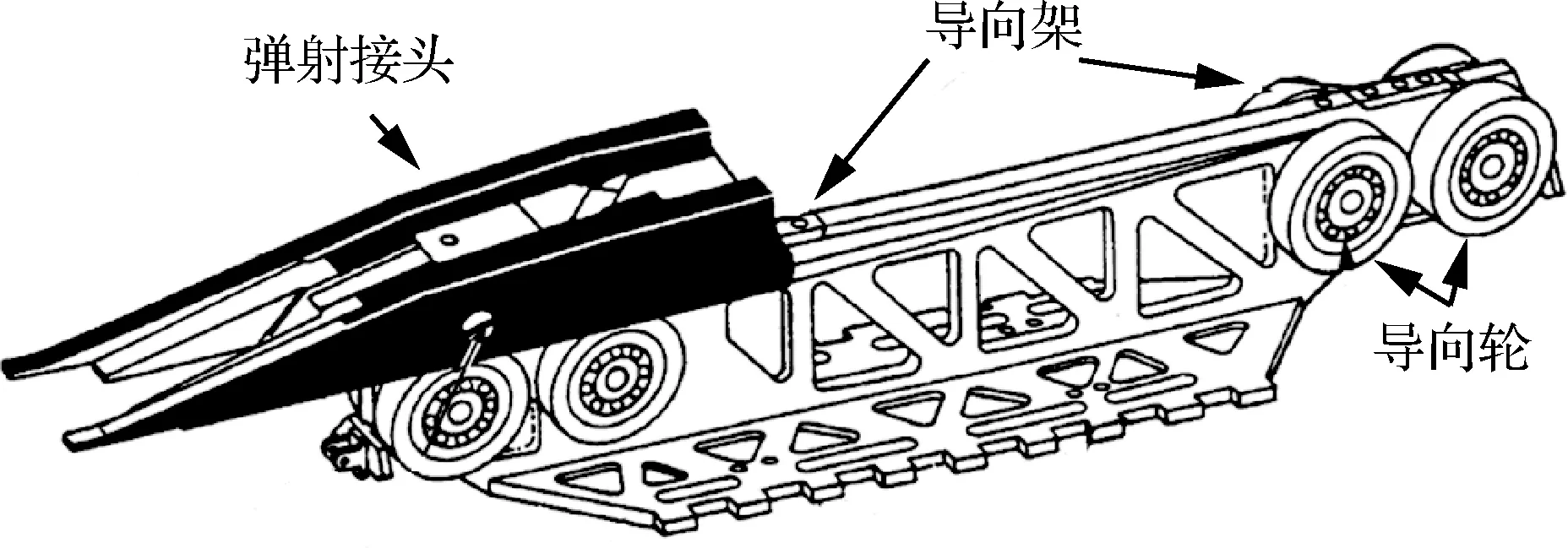
图1 弹射滑车组件示意图图1 Sketch of shuttle assembly

2 计及滑车质量的弹射动力学模型

2.1 动力学模型基本假设

1) 拖拽弹射动力学模型(图2)中，只考虑飞机对称面内的运动，不考虑飞机的侧滑、滚转和偏航。保留：机身在其对称面内的3个自由度(纵向位移xb、垂向位移yb和俯仰角φ)；前、主起落架缓冲器行程(sn和sm)；前、主机轮转动自由度(βn和βm)；前起落架支柱与机身构造线夹角自由度θn；弹射滑车位移自由度xe。

2) 飞机机身和起落架作为刚体处理；牵制杆、弹射杆以及前起落架撑杆简化为线弹性杆。

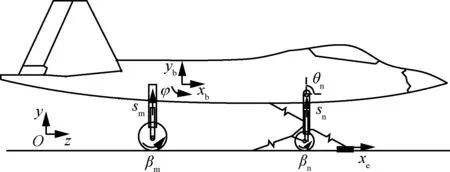
图2 舰载机拖曳弹射动力学模型Fig.2 Dynamic model of carrier-based aircraft tow catapulting

2.2 弹射滑车与前起落架耦合动力学模型

图3给出了舰载机前起落架弹射机构受力示意图。图中：Oxy为全局坐标；Pb为飞机质心位置；Pn为前起落架转轴位置；Pc为前起落架支柱与撑杆的交点；Pd为撑杆与机身的交点；Ps为上防扭臂与前起落架支柱的交点；Pl为防扭臂与牵制杆的交点；Px为下防扭臂与前起落架活塞杆的交点；Pt为弹射杆与支柱的交点；Pe为弹射杆与弹射滑车的交点；Pq为牵制杆与地面的交点；θs和θx分别为上下防扭臂与前起落架支柱轴线的夹角；θq为牵制杆与道面的夹角；θt为弹射杆与道 面的夹角；θc为撑杆与前起落架支柱轴线的夹角。

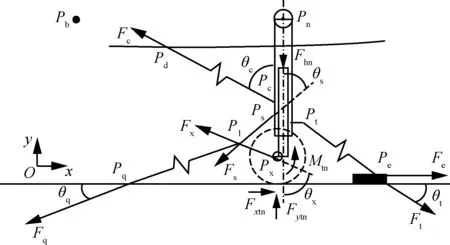
图3 弹射机构受力示意图图3 Sketch of force applied to launch mechanism

弹射机构的外力包含：Fxtn和Fytn为前起落架轮胎水平和垂直载荷；Mtn为前起落架轮胎滚动力矩；Fe为弹射器牵引力。弹射动力学模型的内力包含：Ft为弹射杆轴向载荷；Fc为前起落架撑杆轴向载荷；Fq为牵制杆轴向载荷。

弹射机构的内力包含：Fs为上防扭臂拉压截荷；Fx为下防扭臂拉压载荷；Fhn为前起缓冲器轴向载荷。

由图3可以得到上下防扭臂与前起落架支柱轴线的夹角表达式为

(1)

(2)

式中：L1s为上防扭臂长度；L1x下防扭臂长度；Lsx0为缓冲器全伸长状态下Ps与Px之间的距离。

牵制杆位置矢量rql表达式为

rql=rob+rbn+rns+rsl-roq

(3)

式中：rob和roq分别为Pb和Pq在全局坐标系下的位置矢量；rbn为Pb至Pn的矢量；rns为Pn至Ps的矢量；rsl为上防扭臂位置矢量。

牵制杆与地面的夹角表达式为

(4)

式中：rx为x方向的单位矢量；ry为y方向的单位矢量。

弹射杆位置矢量rte的表达式为

rte=roe-(rob+rbn+rnt)

(5)

式中：roe为Pb在全局坐标下的位置矢量；rnt为Pn至Pt的矢量。

弹射杆与地面的夹角表达式为

(6)

式中：rot为Pe在全局坐标下的位置矢量；Lt0为弹射杆自由状态下的长度。

2.3 弹射器动力学模型

本文旨在分析弹射动力学建模时计及弹射滑车和不计及弹射滑车2种情况下弹射动力学模型动态响应计算结果的差异。因此在建立弹射器模型时分为2种情况分别建模。

在计及弹射滑车质量的弹射动力学模型中，按照弹射杆为线弹性杆的假设，弹射杆轴向载荷Ft由弹射杆的拉伸变形确定，Ft的表达式为

(7)

式中：Kt和Ct分别为弹射杆的轴向刚度和阻尼系数；rte为弹射杆位置矢量。

式(7)中，rte与弹射滑车位移相关，需要建立弹射滑车沿弹射器轨道运动的动力学模型。弹射滑车在弹射器牵引力Fe和弹射杆载荷Ft的共同作用下，沿着弹射器轨道方向运动的动力学方程为

(8)

式中：me为弹射滑车质量。

在不计及弹射滑车质量的拖拽弹射动力学模型中，不包含弹射滑车，不存在弹射滑车的动态响应，那么式(7)和式(8)不再适用。建模时将弹射器牵引力Fe直接作用在弹射杆头部，如图4所示(图中Fv为弹射杆头部竖直方向的约束力)。弹射杆轴向载荷Ft直接由弹射器牵引力Fe通过力的三角形合成原理计算得出，那么Ft表达式为

(9)

在舰载机拖拽滑跑过程中，θt随着前起落架缓冲器压缩量和轮胎的压缩量变化而变化，Ft也受θt和Fe的影响而不断变化。

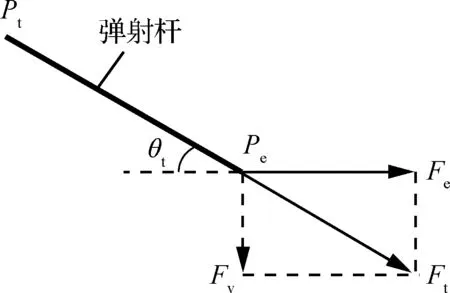
图4 弹射杆受力分析(不计及弹射滑车)图4 Analysis of force applied on catapult link (without catapult shuttle)

2.4 舰载机弹射拖拽动力学模型

在牵制杆与前起落架防扭臂解锁之前，按照牵制杆为线弹性杆的假设，牵制杆轴向载荷Fq的表达式为

(10)

式中：Kq和Cq分别为牵制杆的轴向刚度和阻尼系数；Lq0为牵制杆自由状态下的长度。

弹射器启动后，牵制杆载荷超过解锁阈值后，牵制杆与前起落架解锁，牵制杆载荷为零，即

Fq=0

(11)

下防扭臂张紧载荷Fx表达式为

(12)

前起落架非弹性质量(包含活塞杆和机轮)沿支柱轴线方向运动的动力学方程为

(13)

式中：mhn为前起落架活塞杆质量；mtn为前起落架机轮质量；ln为前起落架与飞机质心的距离。

前起落架撑杆矢量rcd表达式为

rcd=rbn+rnc-rbd

(14)

式中：rnc为Pn至Pc的矢量；rbd为Pb至Pd的矢量。

按照前起落架撑杆为线弹性杆的假设，前起撑杆轴向载荷Fc的表达式为

(15)

式中：Kc和Cc分别为前起落架撑杆的轴向刚度和阻尼系数；Lc0为前起落架撑杆自由状态下的长度。

前起落架绕其安装点Pn的转动方程为

Ftsin(θt+φ+θn)lnt-Fccos(θc)lnc+

Fxtn(sn-sn0)-Fq(rql×rnl)/|rql|

(16)

式中：mzn为前起落架支柱筒质量；Jn为前起落架绕Pn点的转动惯量；lnt为Pn点与Pt点的距离；lnc为Pn点与Pc点的距离；rnl为Pn至Pl的矢量。

前起落架机轮转动角加速度方程为

(17)

式中：Jtn为前起落架机轮对轮轴的转动惯量；Rtn为前起落架轮胎的回转半径。

图5给出了舰载机弹射起飞过程的全机受力分析示意图，按照基本假设式(1)，仅考虑飞机对称面内的力和力矩。图中：Ftb为发动机推力；Fhm为主起落架缓冲器轴向载荷；Fxa、Fya和Ma为飞机气动力和力矩在全局坐标系下的分量。

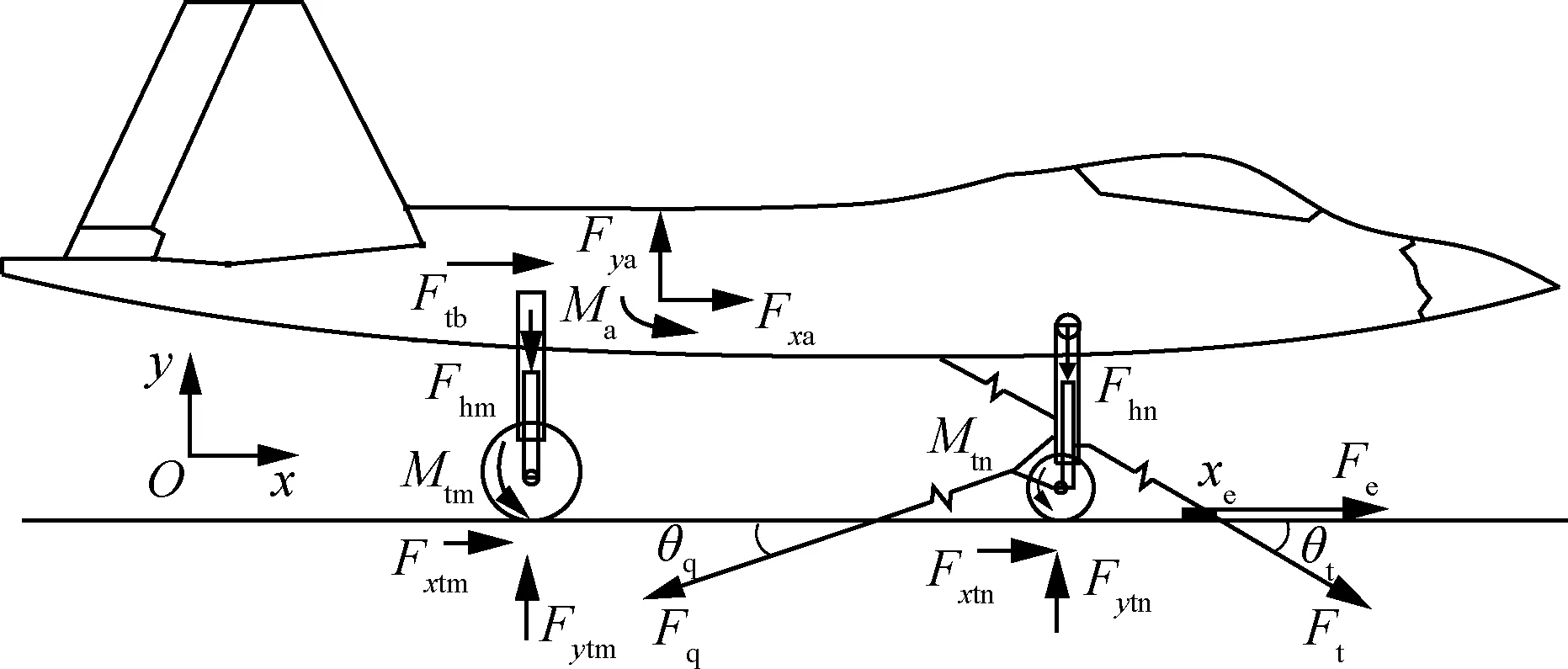
图5 舰载机弹射过程受力分析图5 Analysis of forces applied to carrier-based aircraft in catapulting

主起落架非弹性质量(包含前起落架活塞杆、机轮)沿缓冲器轴线方向的动力学方程为

(18)

式中：lm为飞机质心到主起落架的距离。

主起落架机轮转动角加速度方程为

(19)

式中：Jtm为主起落架机轮对轮轴的转动惯量；Mtm为主起落架机轮的滚阻力矩；Rtm为主起落架轮胎的回转半径。

舰载机的平动动力学方程为

(mb+2(mzm+mhm+mtm)+mzn+mhn+2mtn)·

(20)

式中：mb为飞机机身质量；mzn和mzm分别为前、主起落架支柱筒质量；sn0和sm0分别为前、主起落架缓冲器全伸长状态下轮轴与机身质心的垂向距离。

坐标转换矩阵A(φ)及其对φ的导数表达式为

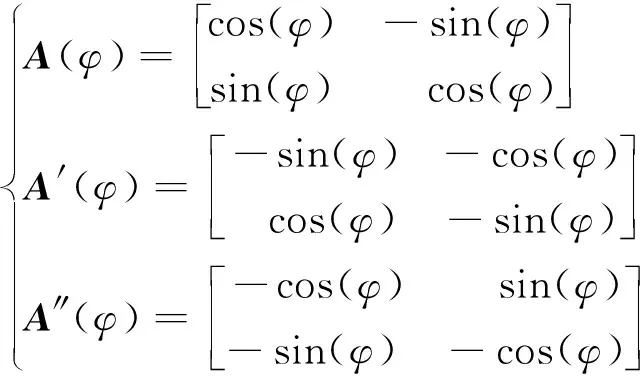
(21)

舰载机俯仰转动的动力学方程为

Ft(ret×rbt)/|ret|-Fq(rql×rbl)/|rql|

(22)

式中：Jb为飞机机身对重心的俯仰转动惯量；Jn和Jm分别为前、主起落架活塞杆对自身重心的俯仰转动惯量。

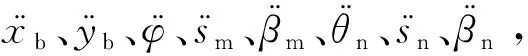
3 拖拽弹射过程动力学分析

采用本文建立的拖拽弹射动力学模型对某舰载无人机拖拽弹射过程进行了分析，动力学模型主要参数如表1所示，并且对比了弹射滑车质量对该舰载无人机拖拽弹射过程前起落架纵向、垂向动态响应以及无人机姿态响应的影响。

为了使计及弹射滑车质量的弹射动力学模型和不计及弹射滑车的动力学模型计算结果具有可比性，本文令两个模型的弹射设计加速度相等。在该无人机弹射加速度为30.0 m/s2的条件下，按式(23)配置弹射器牵引力的设计值。可以得到计及弹射滑车质量的动力学模型中Fe的设计值为180.2 kN，不计及弹射滑车的模型中Fe的设计值为90.2 kN。

Fe=30.0(mb+me)-Ftb

(23)

采用该无人机的弹射力变化曲线按弹射牵引力设计值等比例变换得到计及弹射滑车质量的弹射动力学模型和不计及弹射滑车质量的动力学模型中弹射器牵引力输入随时间的变化趋势，如图6 所示。

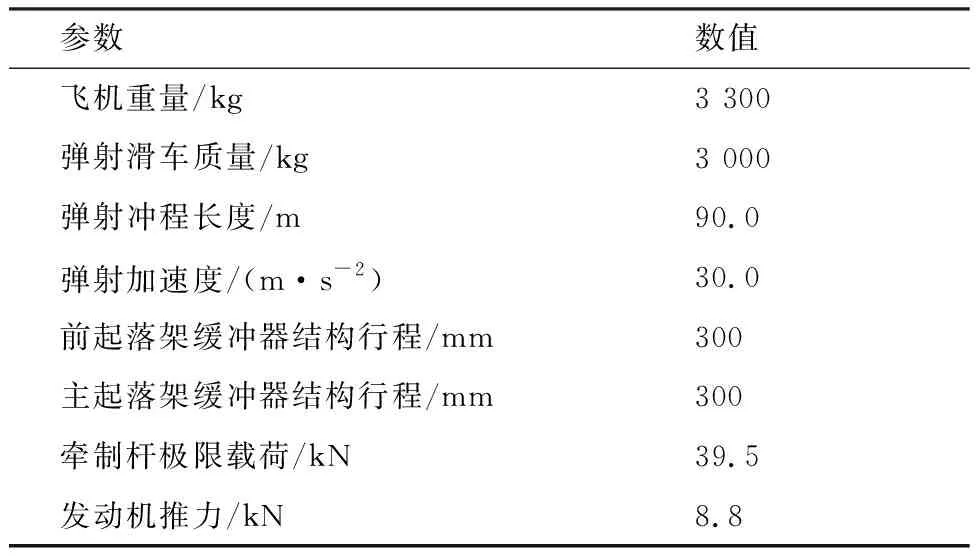
表1 主要仿真参数Table 1 Main parameters of simulation

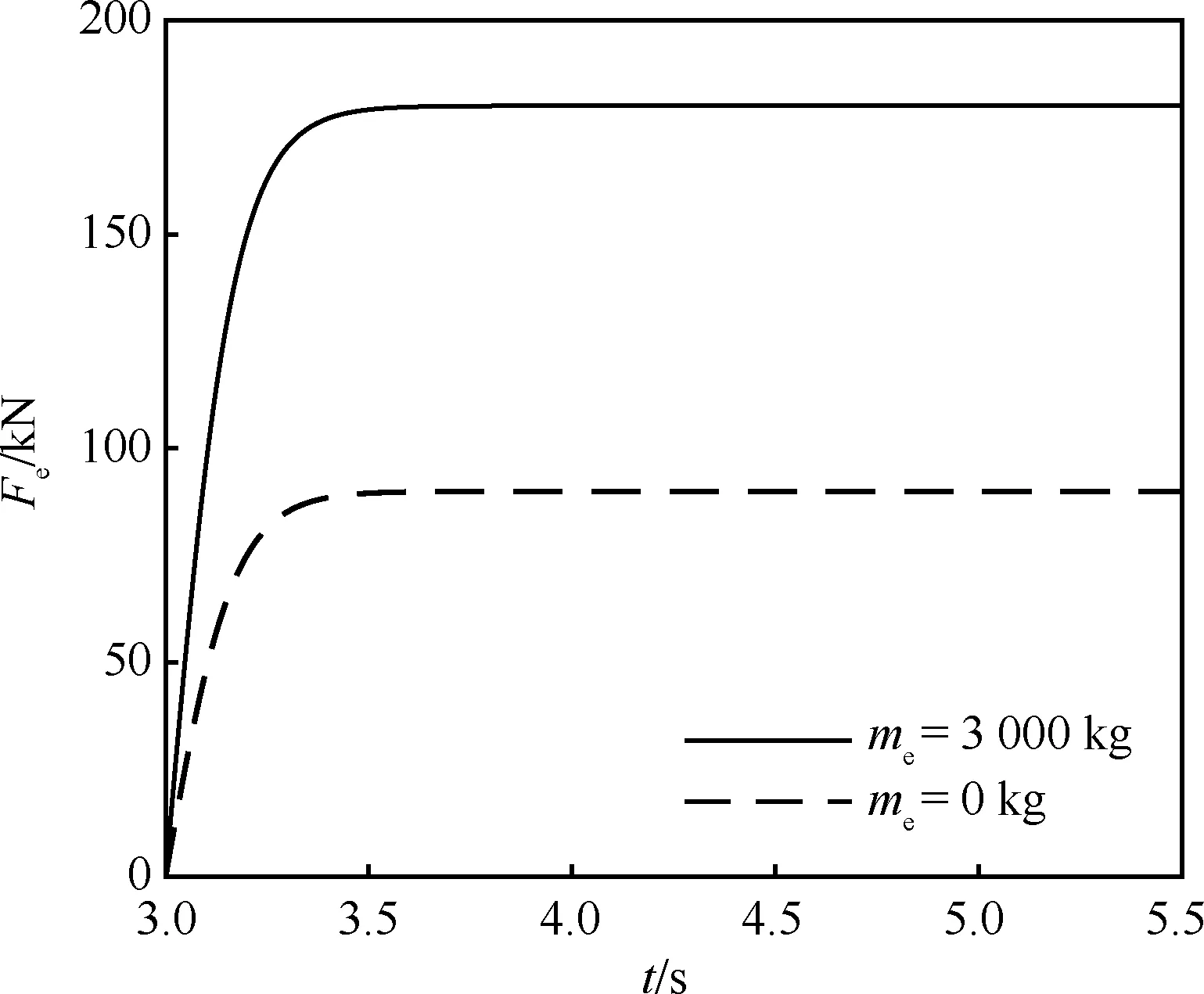
图6 弹射力时间历程图6 Time history of catapult force

3.1 前起落架纵向动态响应对比

前起落架弹射纵向动态响应主要通过为前起落架撑杆载荷和弹射杆载荷响应来表征。

图7为舰载无人机弹射过程牵制杆解锁前后的前起落架撑杆载荷时间历程，图中前起落架撑杆载荷曲线的转折点对应的时间轴为牵制杆解锁时刻。仿真时间为3.0 s时刻启动弹射器，由于弹射滑车惯性的影响，弹射力向前起落架传递过程中有延迟，系统响应变慢。如图7中红色圆形区域所示，即使图6中计及弹射滑车质量的弹射力随时间的增长斜率更大，牵制杆解锁时间仍然推迟了11.0 ms。引入弹射滑车质量后，如图7中红色矩形区域所示，前起落架撑杆载荷高频振荡频率从90.9 Hz降至26.3 Hz；载荷波动从85.4 kN变为93.5 kN，增加了9.5%；载荷峰值从99.8 kN变为123.2 kN，增加了23.4%(见表2)。

图8给出了弹射杆载荷时间历程，在不计及弹射滑车质量时，弹射杆载荷按照式(9)计算，与弹射器载荷相关，逐渐增加。计及弹射滑车质量以后，弹射杆载荷与弹射滑车动态响应相关，在牵制杆解锁瞬间，前起落架支柱向前弹出，弹射滑车的惯性使得弹射杆出现短暂的卸载过程(图8中红色矩形区域)，随后载荷再次增加，呈现61.0 kN的载荷波动，载荷峰值达到112.6 kN，相对于不计及弹射滑车质量的弹射拖拽模型，载荷峰值增加了21.6%(见表2)。

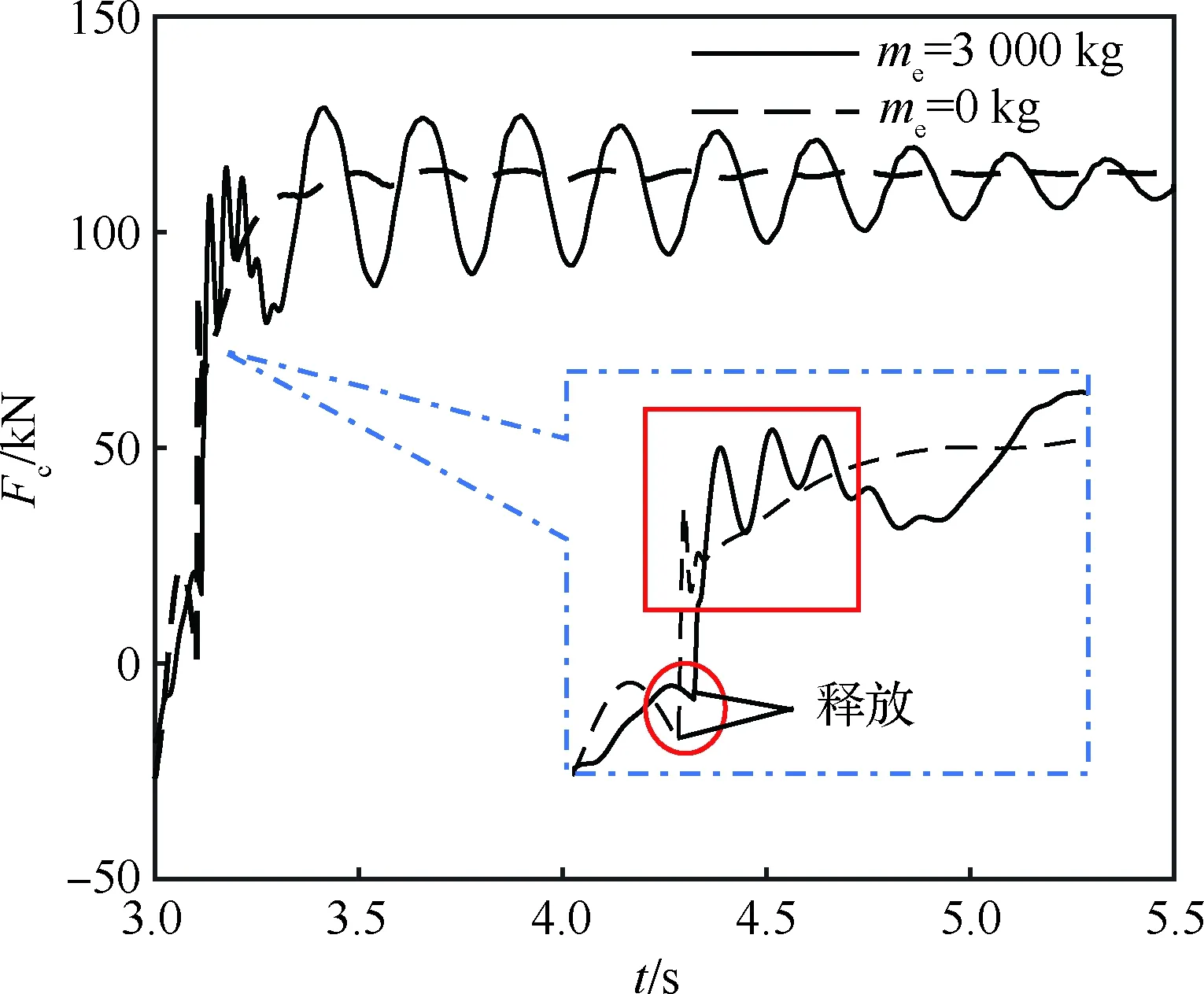
图7 前起落架撑杆载荷时间历程图7 Time history of nose landing gear strut load

图8 弹射杆载荷时间历程图8 Time history of launch bar load

表2 纵向动态响应分析结果Table 2 Results of course dynamic response analysis

参数me=0 kgme=3 000 kg偏差/%撑杆载荷峰值/kN99.8123.223.4弹射杆载荷峰值/kN92.7112.621.6撑杆载荷波动量/kN85.493.59.5弹射杆载荷波动量/kN61.0撑杆载荷波动频率/Hz90.926.3-71.1弹射杆载荷波动频率/Hz26.3

3.2 前起落架垂向动态响应对比

前起落架弹射垂向动态响应主要表现为前起落架缓冲器压缩量以及前起落架垂向载荷响应规律。

图9给出了无人机弹射过程中前起落架缓冲器压缩量变化曲线，计及弹射滑车质量以后，前起落架缓冲器压缩量变化范围明显增大，从20.4 mm增加到26.6 mm，增加了30.4%(见表3)。并且，前起落架缓冲器压缩量振荡衰减也更缓慢，在弹射器到达弹射行程末端时，计及弹射滑车质量的模型计算的前起落架缓冲器行程振幅为4.7 mm，不计及弹射滑车质量的模型计算结果仅为1.8 mm。

图10给出了前起落架轮胎垂向载荷变化曲线，由于计及弹射滑车质量的弹射动力学模型中整个弹射系统的惯性增加，前起落架垂向振荡的幅度变大。前起落架轮胎垂向载荷峰值从58.0 kN增加到66.1 kN，增加了14.0%，同时垂向动态响应频率从5.2 Hz降到了4.4 Hz(见表3)。

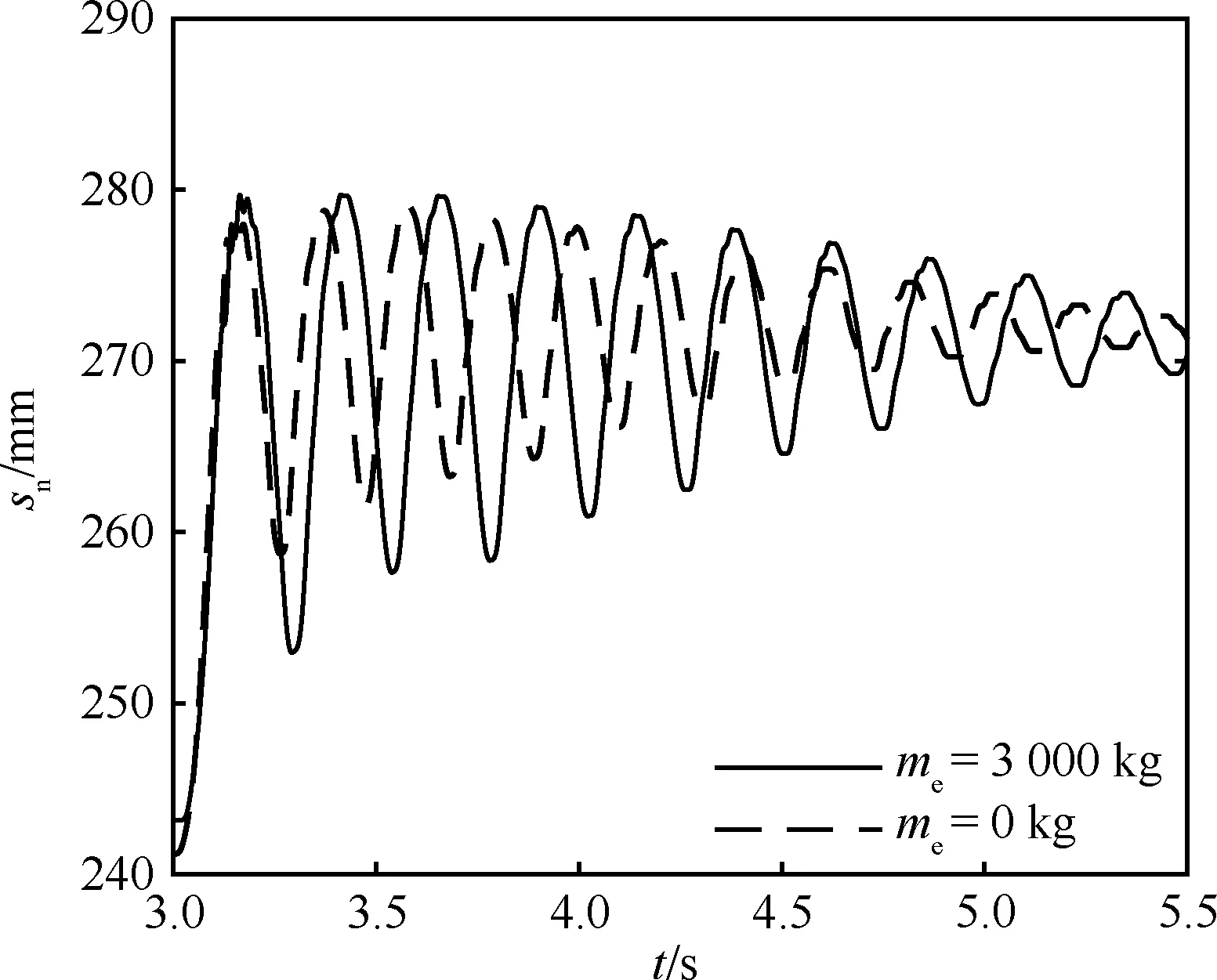
图9 前起落架缓冲器压缩量时间历程图9 Time history of nose landing gear stroke

表3 垂向动态响应分析结果Table 3 Results of vertical dynamic response analysis

参数me=0 kgme=3 000 kg偏差/%前起落架缓冲器压缩量波动量/mm20.426.630.4前起落架轮胎垂向载荷峰值/kN58.066.114.0前起落架轮胎垂向载荷波动频率/Hz5.24.4-15.4

图10 前起落架轮胎垂向载荷历程Fig.10 Time history of nose landing gear tire vertical load

3.3 无人机弹射姿态响应对比

图11给出了无人机拖拽弹射过程中的俯仰角变化曲线，由于计及弹射滑车质量以后前起落架缓冲器压缩量变化幅度更大，使得无人机弹射过程中的俯仰姿态角变化范围从-1.06°～0.09°扩大至-1.14°～0.28°。图12给出了无人机拖拽弹射过程中的俯仰角速率变化曲线，与俯仰角变化规律相比，俯仰角速率受弹射滑车的影响较小，变化范围从-15.1～15.26 (°)/s扩大至-15.4～ 17.2 (°)/s。

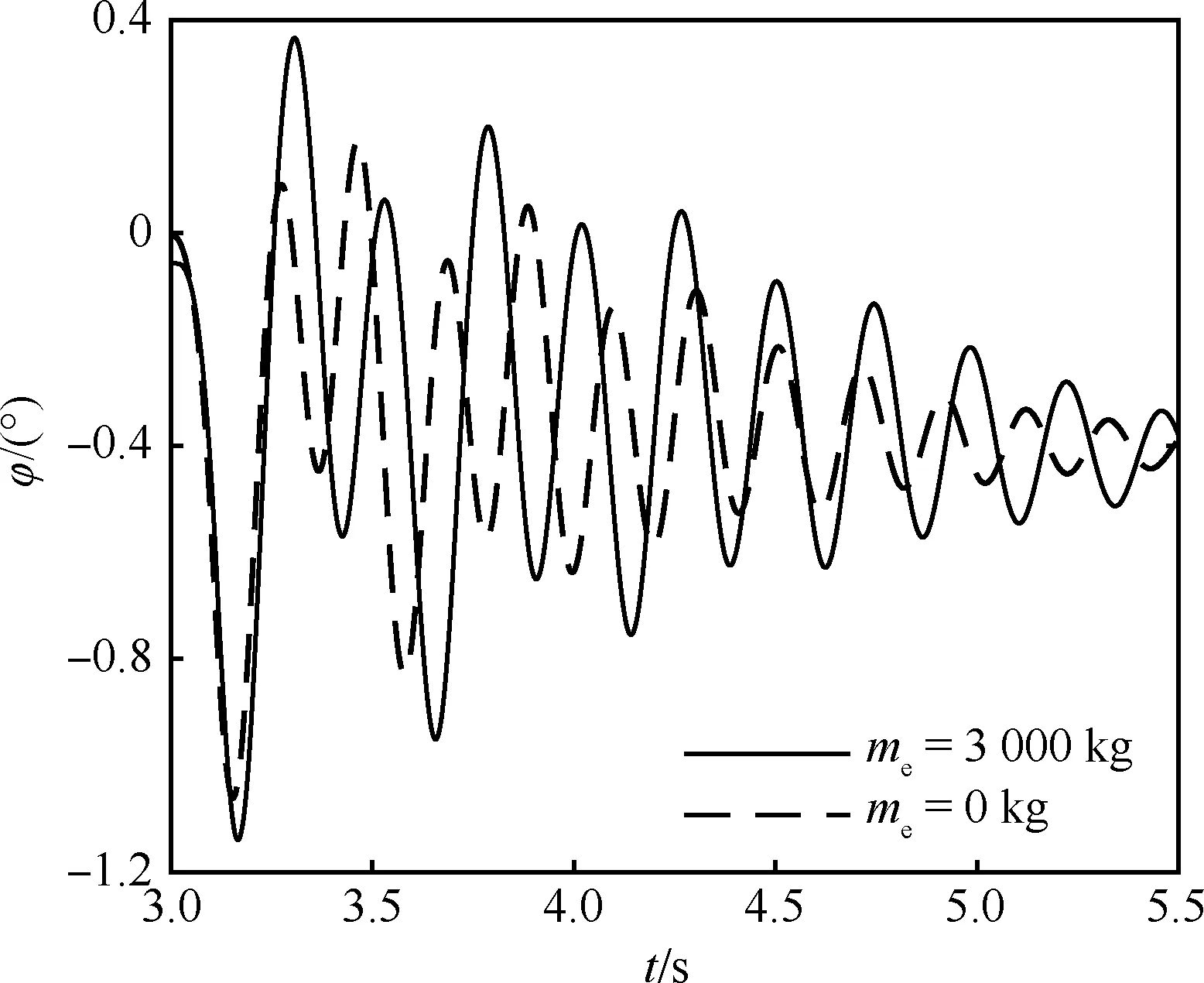
图11 俯仰角随时间变化曲线图11 Variation of pitch angles over time

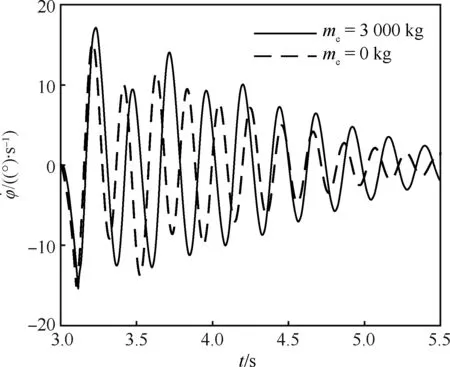
图12 俯仰角速率随时间变化曲线图12 Variation of pitch angle velocities over time

4 结 论

在对由某无人机改造的弹射型研发设计中发现，当飞机起飞重量和滑车重量相当时，弹射滑车质量对于舰载无人机弹射动力学影响较大，通过对比无人机弹射动态响应计算结果得出以下结论供舰载机设计人员，尤其是舰载无人机设计人员参考。

1) 舰载机拖拽弹射过程中，弹射滑车的惯性力会沿着弹射杆传递到前起落架上，改变前起落架的动态响应。

2) 弹射滑车质量的引入，降低了舰载机弹射拖拽过程的高频响应频率，对于该无人机弹射过程，弹射滑车使得前起落架纵向响应频率从90.9 Hz降到26.3 Hz。

3) 弹射滑车质量的引入，增加了舰载机拖拽弹射过程中前起落架的载荷峰值，对于该无人机弹射过程，弹射滑车使前起落架撑杆载荷峰值增加了23.4%，弹射杆载荷峰值增加了21.6%，前轮垂向载荷增加了14.0%。

4) 弹射滑车质量的引入，使得该无人机弹射过程中前起落架垂向响应频率从5.2 Hz降到4.4 Hz， 前起落架缓冲器压缩量变化范围增加了30.4%，进而扩大了弹射过程中无人机俯仰姿态角和角速度的变化范围。