基于卷积神经网络技术的直升机旋翼谱识别方法

王志诚，徐 卉，梁小溪，王 珺，周起华，朱 骏

(1.上海交通大学 电子信息与电气工程学院，上海 200240； 2.上海无线电设备研究所，上海 201109；3.上海机电工程研究所，上海 201109)

0 引言

现代雷达是利用不同飞机目标对电磁波反射的物理特性的差异，基于一定识别技术来实现目标的区分。通常目标识别技术由数据获取、数据预处理、特征提取、目标识别组成[1]。其中目标识别是根据已有的训练样本集，基于一定的训练规则，判断决策被识别对象。

现有的雷达目标识别方法包括卷积神经网络(CNN)、支持向量机(SVM)方法、贝叶斯方法、隐马尔可夫模型方法等。其中，CNN的稳健性较好，具有更强的信息表达与建模能力，能更准确地处理分析信息，在目标识别等方面得到广泛应用。杜兰等[2]提出基于时域回波相关性特征的飞机目标分类方法，其利用支持向量机方法，结合仿真与实测数据证明：在脉冲重复频率较低且多普勒谱存在一定程度混叠时，时域相关性特征仍表现出相对较好的目标分类性能。詹武平等[3]在基于深度神经网络模型的雷达目标识别中给出了深度神经网络模型识别目标算法，利用仿真数据验证该识别方法的准确性，并通过数值实验结果表明该方法能较准确地识别雷达跟踪目标。

运动中的直升机旋翼具有丰富的频谱特征，可采用频域维度目标识别方法，实现直升机目标识别。与时域维度研究目标特征的常规方法不同，本文根据不同目标在频域维度的特征差异，结合卷积神经网络的卷积核技术，实现直升机目标识别，为直升机目标的可靠识别提供了一种新的思路。

1 现代雷达与卷积神经网络

在机器学习中，CNN已成功应用于图像识别[4]。20世纪60年代，Hubel和Wiesel在研究猫脑皮层中用于局部敏感和方向选择的神经元时，发现其独特的网络结构可有效地降低反馈神经网络的复杂性，继而提出了CNN的概念。现在，CNN已成为众多科学领域的研究热点之一，特别是在模式分类领域，由于该网络避免了前期对图像的复杂预处理，可以直接输入原始图像，所以得到了更为广泛的应用。

现代雷达的信号处理系统可获得与光学图像或红外图像类似的“雷达图像”，比如距离角度联合的极坐标图、时频二维分布图、合成孔径图等。图1为时频二维分布图。其中，t为时间，f为频率，U为目标回波的幅度[5]。图中2个尖峰位置代表回波中存在2个目标。根据目标回波在二维数组中的位置，可以明确目标在时域、频域、幅度域的分布，获取目标的距离、速度、能量等信息，进一步实现目标识别。

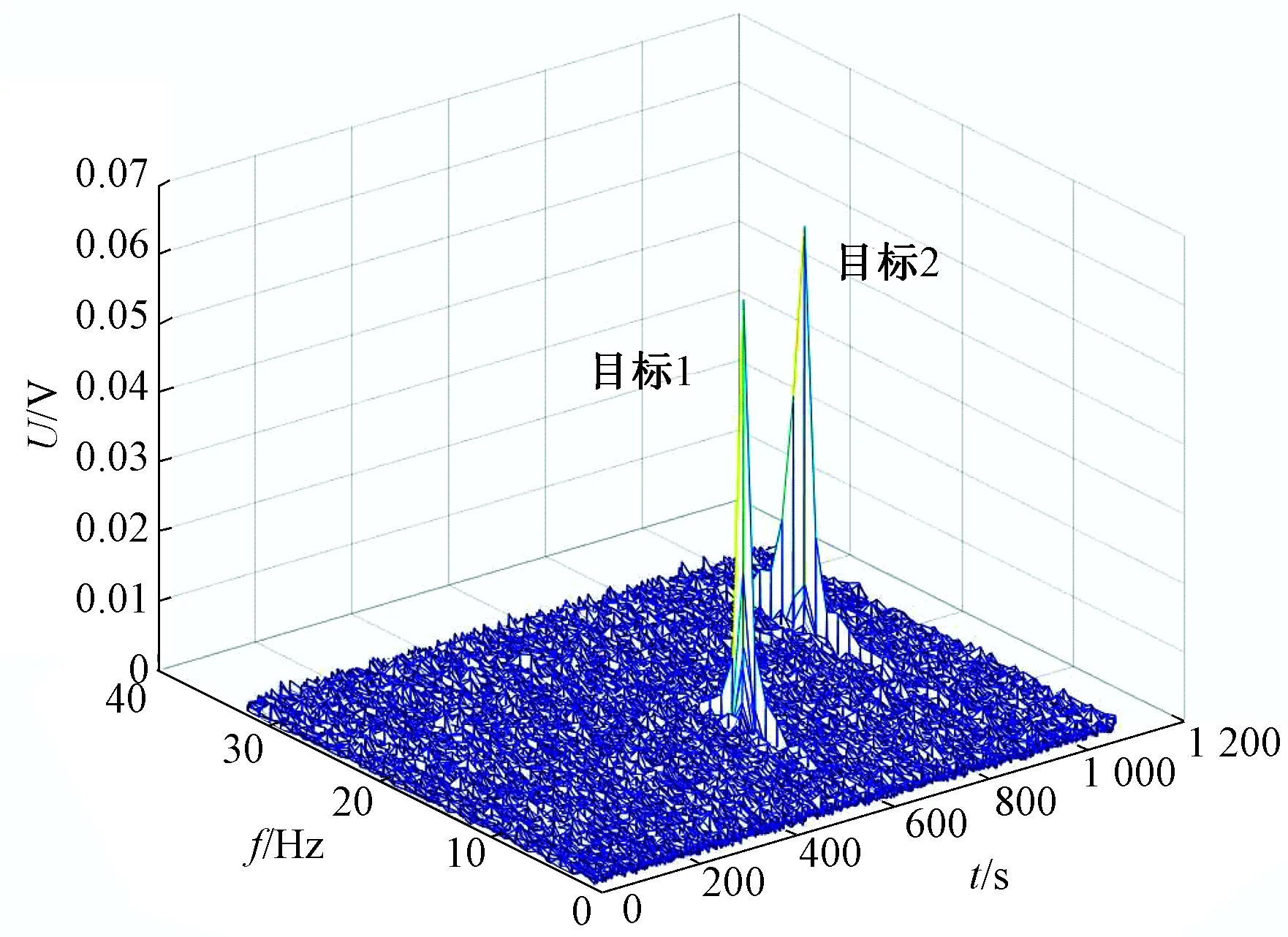
图1 雷达回波的时频二维分布Fig.1 Time-frequency distribution of radar echo

利用卷积神经网络中的特征提取层处理方法实现了雷达目标识别工作。该方法本质上是利用1个二维的滤波器矩阵(卷积核)和1个待处理的二维数组作二维卷积运算。对于二维数组的每一个像素点，计算它的邻域像素和卷积核对应元素的乘积，求和后作为该像素位置的值，该过程称为卷积滤波。卷积核在雷达图像上遍历的过程，类似于模板匹配的过程，即2个矩阵作二维卷积运算。假设矩阵A和矩阵B的尺寸分别为ma×na和mb×nb，则二维卷积运算过程主要分为3步。

第1步：对矩阵A补零。第1行之前和最后1行之后都增加mb-1行0，第1列之前和最后1列之后都增加nb-1列0，如图2所示。

第2步：将矩阵B(卷积核)绕其中心旋转180°，如图3所示。

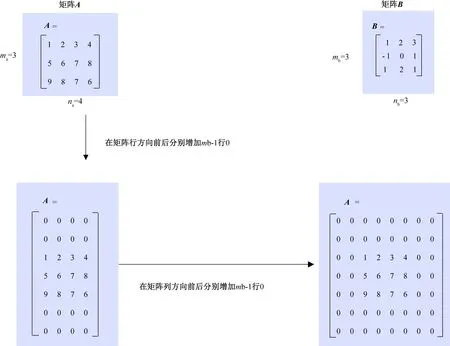
图2 矩阵补零Fig.2 Adding zeros in matrix

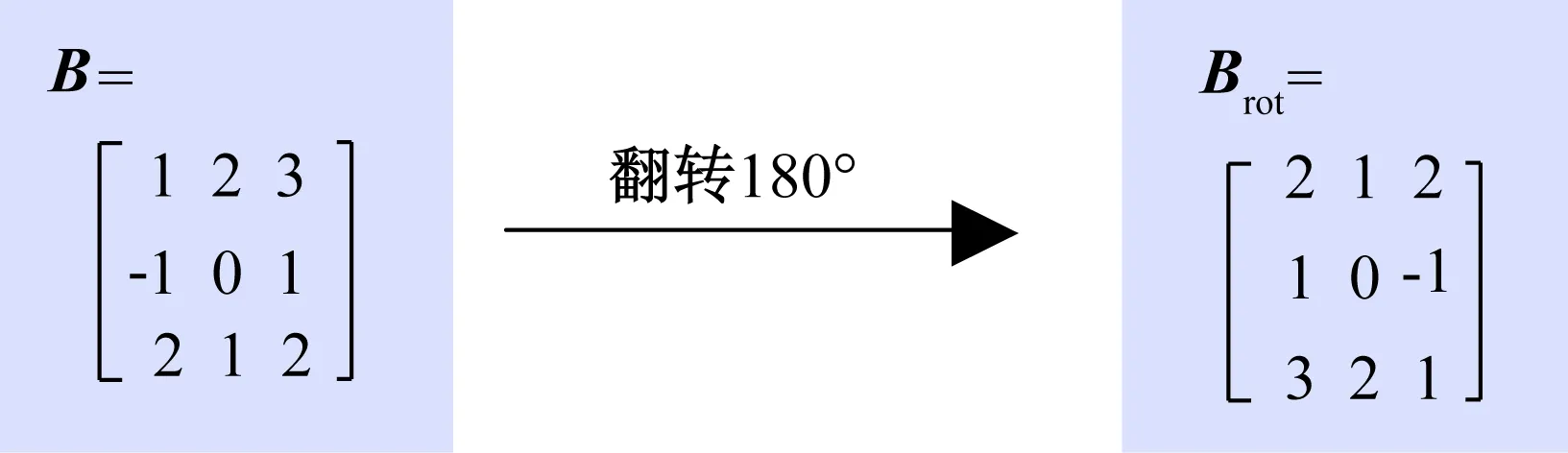
图3 矩阵翻转Fig.3 Matrix inversion

第3步：滑动旋转后的卷积核矩阵Brot，将Brot的中心对准矩阵A的每一个元素，并求乘积和(将旋转后的矩阵Brot在矩阵A上滑动，对应位置相乘后再相加)，如图4所示，位置1表示输出图像的值从当前核的计算值开始(对应输出结果左上角)，位置2表示到该位置结束(对应输出结果右下角)。

完成所有的遍历后，最终输出一个新的二维矩阵。该输出矩阵中包括目标特征信息，可实现目标识别功能。

2 雷达的直升机旋翼回波特征

直升机与其他飞行目标的最大区别在于其具有旋翼。现代雷达系统可以通过分析旋翼回波特征，识别直升机目标。为了确保测距不模糊，现代雷达一般会采用低重复频率(LPRF)工作模式。在该模式下，若目标运动较快，则雷达会出现测速模糊现象。运动中的直升机旋翼处于高速旋转状态，回波速度对于LPRF雷达来说是高度模糊的，导致旋翼回波在时频二维分布图上的分布将呈现特殊性。基于这种特殊性，雷达可以识别直升机目标。

2.1 悬停直升机的雷达回波组成

直升机结构外形如图5所示，其雷达回波主要由机身回波、主旋翼回波、尾桨回波组成[6]。

1) 机身回波

机身回波与一般固定翼飞机目标的回波类似，直升机的雷达散射截面积(RCS)在机首和机尾方向最小约几平方米，而在正侧面可达几十平方米或更大，其多普勒频移取决于相对于雷达的径向速度。当悬停时，其回波无异于固定目标回波。

2) 主旋翼回波

主旋翼回波包括旋翼直接反射以及与机身间的多次反射的回波。在雷达波束垂直照射叶片的一个侧边时，回波达到最强，从而形成周期性峰包[7]。由于空气动力学的原因，现役各种直升机的叶片外端线速度大致相同，约为260 m/s，旋翼转动会形成一定宽度的频谱。单叶片产生的频谱将从零频到最大线速度对应的最大多普勒频率，整体连成一片，当叶片迎着雷达射线方向旋转时，产生正多普勒谱区，当叶片背着雷达射线方向旋转时，将产生负多普勒谱。

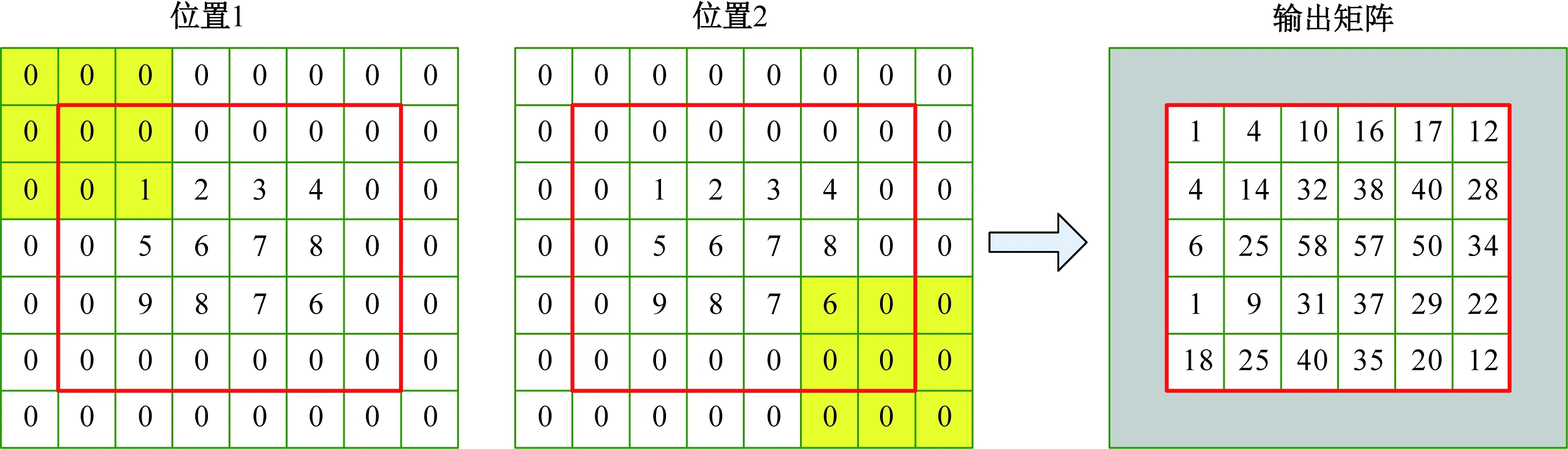
图4 二维卷积过程与输出矩阵Fig.4 Two dimensional convolution process and output matrix

图5 直升机结构外形Fig.5 Structural shape of helicopter

3) 尾桨回波

尾桨回波类似于主旋翼，但叶片直径较小、转速较高，通常是在垂直面内旋转。由于尾桨物理尺寸较小，且易受机身遮挡。雷达波束经常照射不到，导致RCS较小，反射不稳定。

一般情况下，直升机的雷达回波中主要存在机身回波与主旋翼回波[8]。

2.2 旋翼回波时频仿真

雷达获得的直升机主旋翼回波中包含了多个频率信息。桨叶在相同的角速度下，线速度呈现线性变化，雷达在同一时刻将收到多个频率叠加的信号。当叶片朝雷达方向运动时，形成正多普勒谱，而当叶片背向雷达方向运动时，形成负多普勒谱[9]。

出现回波信号最强的时刻是桨叶垂直通过雷达视线的时刻，也就是说，雷达波束一次只能照射到叶片的一个侧边。计算每个叶片的多普勒频率，公式为

(1)

式中：vL为叶片最大线速度；β为雷达入射主波束夹角；λ为雷达工作波长；f为当前叶片产生的多普勒频率。当叶片数目为偶数时，处在脉峰期间的回波脉冲将同时具有正、负2个多普勒谱；当叶片数目为奇数时，正、负多普勒谱交替出现。

当桨叶为偶数时，包含的频率范围为

(2)

仿真分析偶数叶片主旋翼回波时频分布时，参数设置如下：直升机的行进速度v=0 m/s，波长λ=0.015 m，主旋翼桨叶个数N=4，相邻桨叶间夹角为90°；1号桨叶与3号桨叶对称，夹角为180°，2号桨叶与4号桨叶对称，夹角为180°；叶片旋转速度Ω=5 r/s(或5×2π rad/s)，旋转平面与入射主波束的夹角β=30°，叶片旋转初始角θ0=π/8，雷达工作重复频率fr=2 kHz。

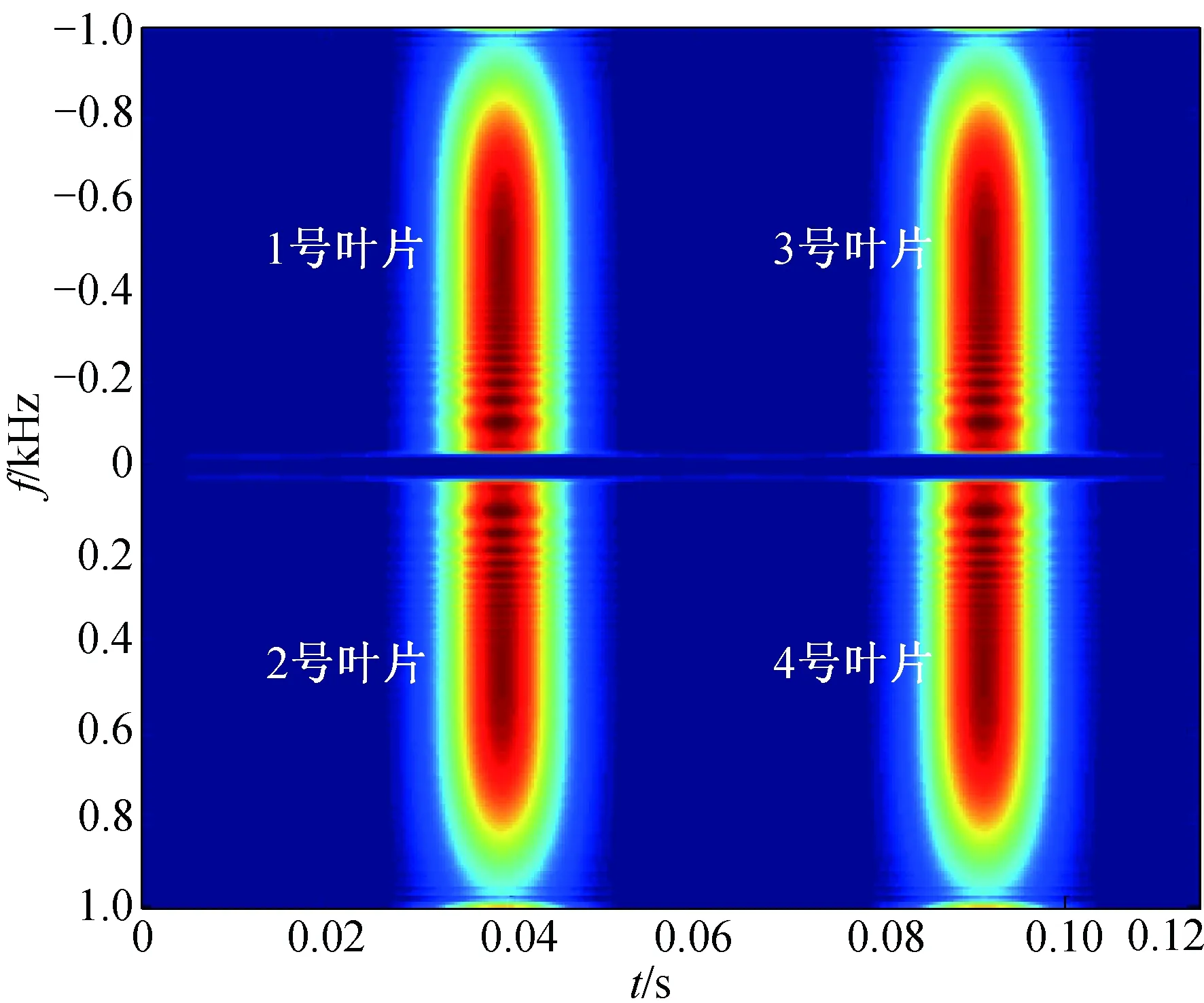
图6 偶数叶片时主旋翼回波时频分布图Fig.6 Time-frequency distribution of main rotor echo for even blades

图6显示了直升机4个主旋翼桨叶的时频分布仿真情况(俯视视角)。由于1号桨叶与3号桨叶对称，则在0.039 s同时采集到两者回波。两叶片角速度相同，旋转方向相对雷达波束照射方向相反，因此多普勒频率与展宽程度相同，符号相反[10]。1号叶片多普勒范围为-1～0 kHz，3号叶片的多普勒范围为0～1 kHz。由于2号桨叶与4号桨叶对称，则在0.091 s采集到两者回波，两叶片多普勒频率范围分别和1号、3号叶片相同。可以看出，当叶片数目为偶数时，正、负2个多普勒谱区域将同时出现。

当桨叶数量为奇数时，包含的频率范围不对称，频率范围可表示为

(3)

(4)

当仿真分析奇数叶片主旋翼回波时频分布时，参数设置如下：直升机行进速度v=0 m/s，波长λ=0.015 m，主旋翼桨叶个数N=5；相邻桨叶间夹角均为72°；叶片旋转速度Ω=5 r/s(或5×2π rad/s)，叶片旋转平面与入射主波束的夹角β=30°，叶片旋转初始角θ0=π/8，雷达工作重复频率fr=2 kHz。

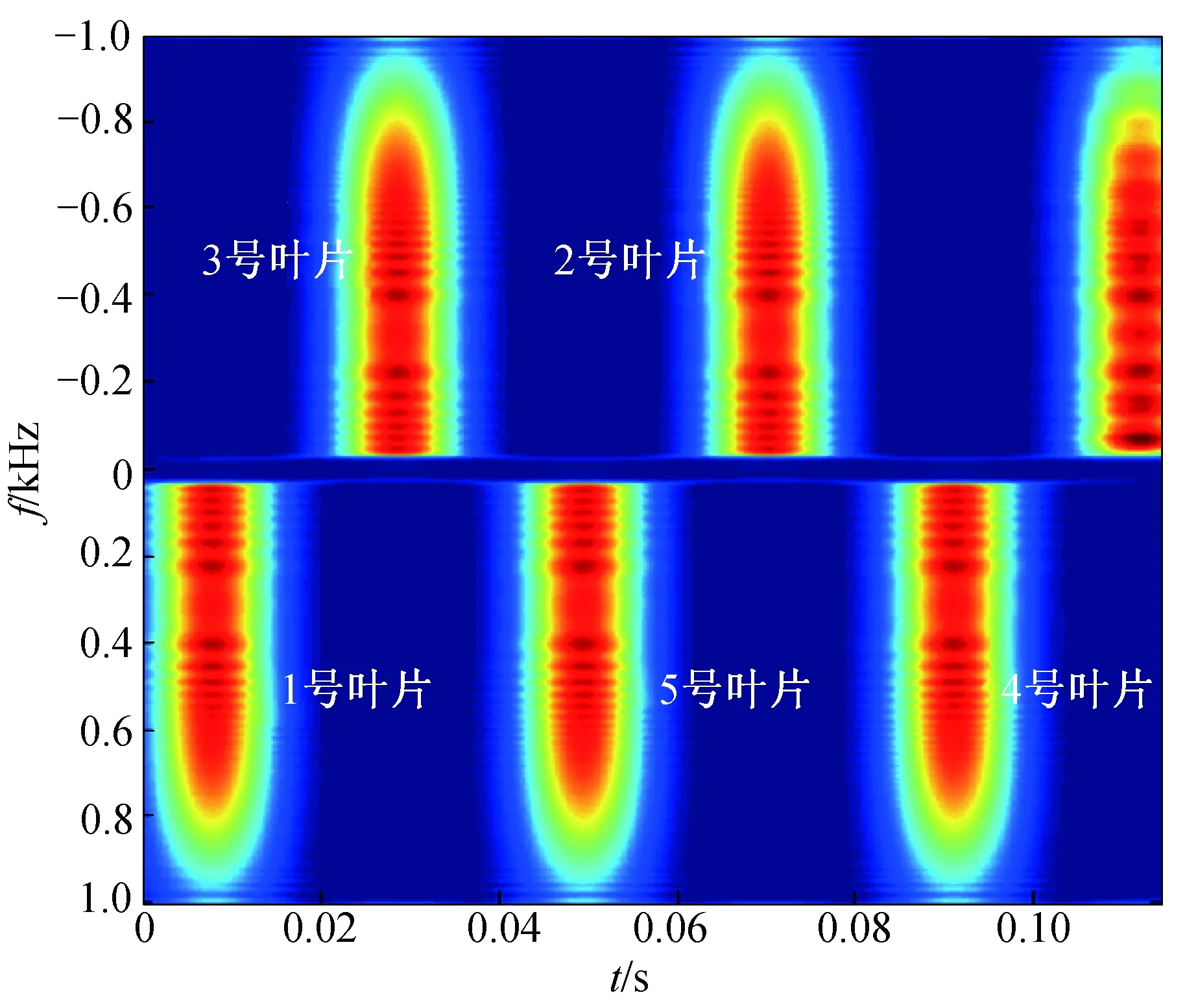
图7 奇数叶片时主旋翼回波时频分布图Fig.7 Time-frequency distribution of main rotor echo for odd blades

图7显示了直升机5个主旋翼桨叶的时频分布仿真情况(俯视视角)。在0.008 s时采集到 1号叶片回波，多普勒范围为0～1 kHz；在0.029 s时采集到2号叶片回波，多普勒范围为-1～0 kHz；在0.050 s时采集到3号叶片回波，多普勒范围为0～1 kHz；在0.071 s采集到4号叶片回波，多普勒范围为-1～0 kHz；在0.092 s时采集到5号叶片回波，多普勒范围为0～1 kHz。由图7可以看出，当叶片数目为奇数时，正、负多普勒谱交替出现。

直升机主桨叶数量无论是奇数还是偶数，高速旋转的叶片都会对雷达信号实施额外调制，导致回波多普勒展宽并占据整个频率范围。

3 利用神经网络卷积核的目标识别过程

直升机旋翼回波沿频率维分布较宽[10]，船只、固定翼飞机等其他类型目标的回波在频率维分布较窄。目标回波在频率维分布宽窄的程度可作为直升机目标识别的特征依据。利用神经网络卷积核技术实现直升机目标识别主要步骤如下。

第1步：根据直升机主旋翼回波在频率维的分布特性，基于大量实测回波数据对直升机回波进行时频二维分析；

第2步：分离直升机机体回波与主旋翼回波；

第3步：训练主旋翼回波，形成卷积神经网络特征提取层的卷积核；

第4步：将卷积核在雷达时频二维分布图上遍历，完成卷积滤波处理；

第5步：分析输出结果，最大值的位置即为直升机主旋翼。

3.1 实测直升机回波时频二维分布图

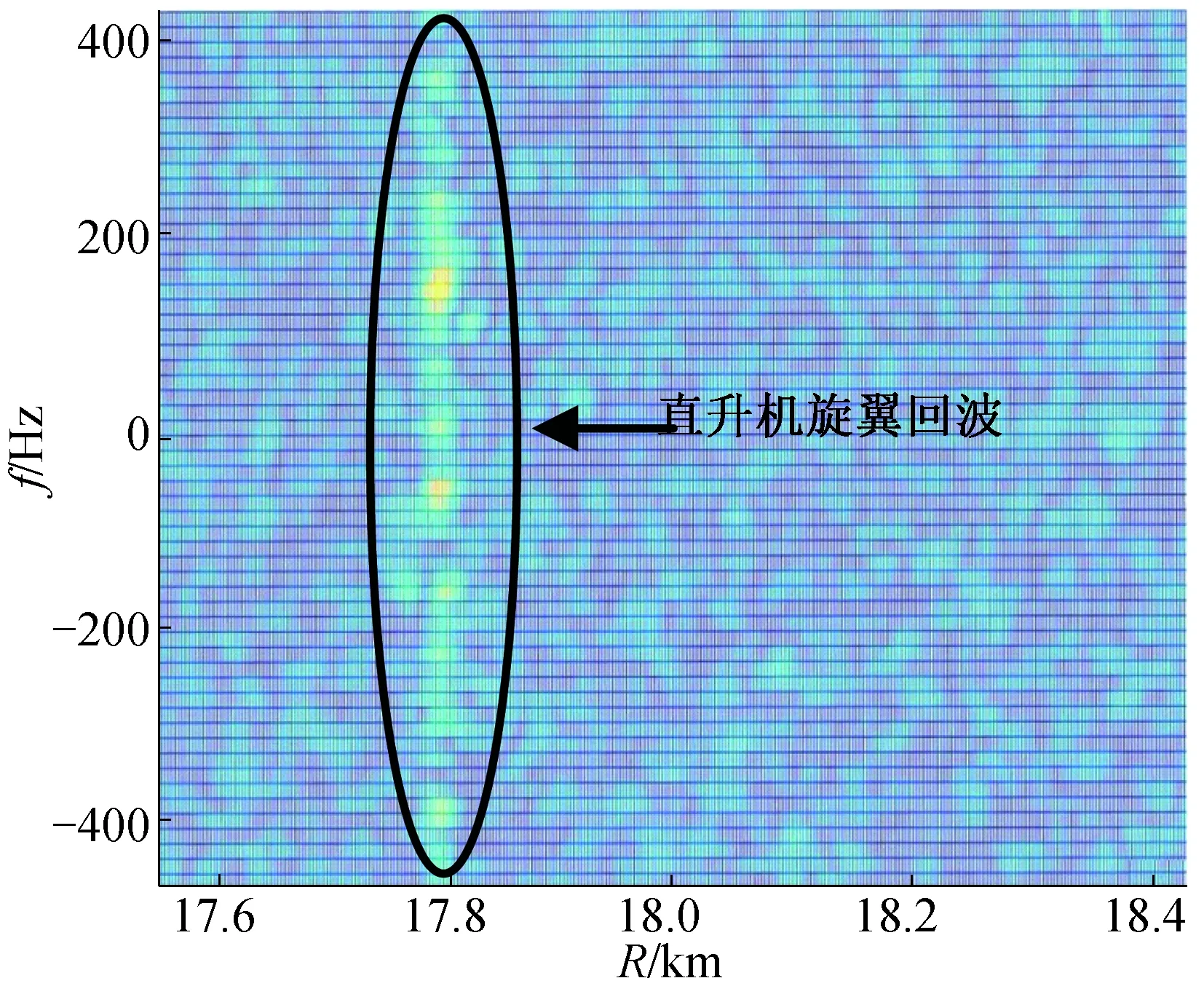
图8 实测直升机回波时频分布图(俯视视角)Fig.8 Time-frequency distribution of measured helicopter echoes (with an overhead view)

根据仿真分析，在LPRF条件下的直升机主旋翼回波在频率维将展宽至整个频率范围。图8为对某型号直升机(主桨叶数为4)实际回波处理后获得的时频二维分布图(俯视视角)。雷达信号参数如下：脉宽为40 μs，相参积累数为64，杂波频率测量范围为-400～400 Hz，杂波距离R测量范围为17.6～18.4 km。不同叶片的回波时间间隔较短，在图中沿距离维聚拢在一起，出现在17.8 km处。直升机主旋翼回波频率范围为-400～400 Hz，呈现出明显的展宽特征，与图6的仿真结果相同。

另外选取不同时刻的4组直升机实测数据，通过斜视视角观察回波时频分布，可以获得直升机悬停时的回波时频分布图，如图9所示。4组实测回波中均包括直升机机体回波与主旋翼回波，均在18.1 km处出现，其中机体回波能量较为集中，呈现“单峰”的形态，幅度范围为12～60 V；主旋翼回波的能量在频率维展宽，幅度范围为4～6 V，呈现连续“多峰”的形态，占据了-400～400 Hz整个频率范围。主旋翼展宽特征与仿真结果一致。

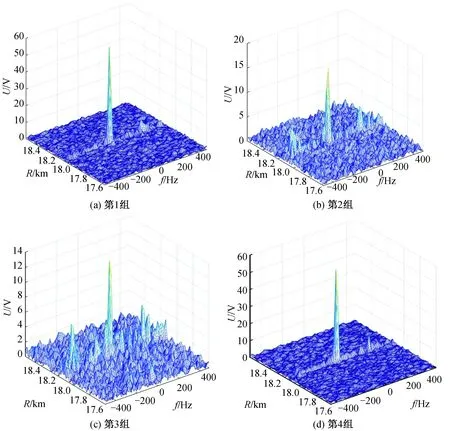
图9 直升机悬停时的回波时频分布图Fig.9 Time-frequency distribution of echo in hovering helicopter

3.2 主旋翼回波

为提取直升机主旋翼回波频谱，需将机体回波从时频分布数据中去除，并保留主旋翼回波。图10为去除机体回波后的直升机主旋翼回波时频分布图。主旋翼回波距离为18.1 km，幅度范围为4～8 V，频率范围为-400～400 Hz。由于直升机相对雷达有静止、远离、接近等多个运动状态，需提取不同运动状态下的直升机主旋翼回波进行训练。经过大量实际采集数据训练后，形成神经网络卷积核矩阵。

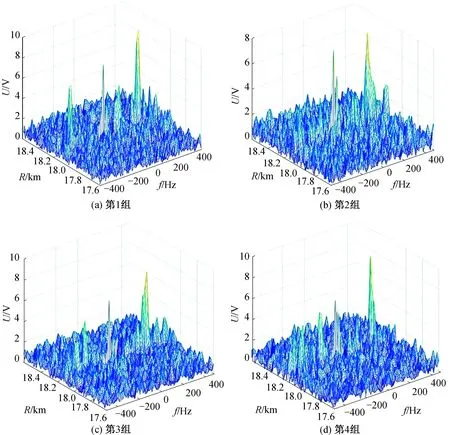
图10 直升机悬停时的主旋翼回波时频分布图Fig.10 Time-frequency distribution of main rotor echo in hovering helicopter

3.3 旋翼神经网络卷积核

根据直升机机体回波的运动方向与运动速度，采用实测的1 000组入射角为0°的直升机回波数据作为样本进行训练，获得神经网络卷积核矩阵。训练后的卷积核矩阵如图11所示，每个卷积核矩阵的尺寸为13×64，采用归一化幅度，距离维与频率维均为点数。经过实测数据训练的神经网络卷积核，主要表征了直升机旋翼回波在频率维度的扩展特征。特征提取时需要将卷积核矩阵与当前雷达回波时频分布图进行二维卷积运算。

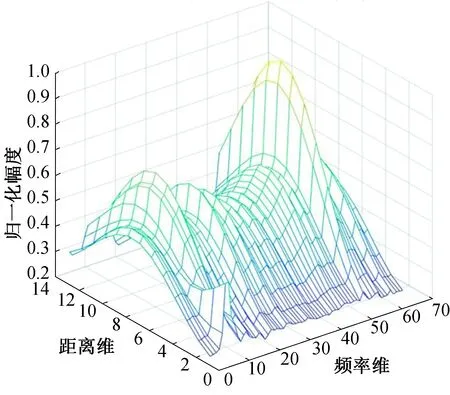
图11 经过实测数据训练的神经网络卷积核Fig.11 Neural network convolution kernel trained by measured data

3.4 识别

神经网络卷积核与待识别的时频二维分布图作二维卷积运算，输出新的二维矩阵。当卷积核与主旋翼回波实现最佳匹配后，输出的二维矩阵中将出现类似山脊状图形。直升机主旋翼回波经过卷积神经网络后的输出矩阵如图12所示。图中，山峰为最大值，其余值以最大值为中心，沿频率维呈现对称下降分布。该最大值在距离维上的位置即为直升机主旋翼回波位置。

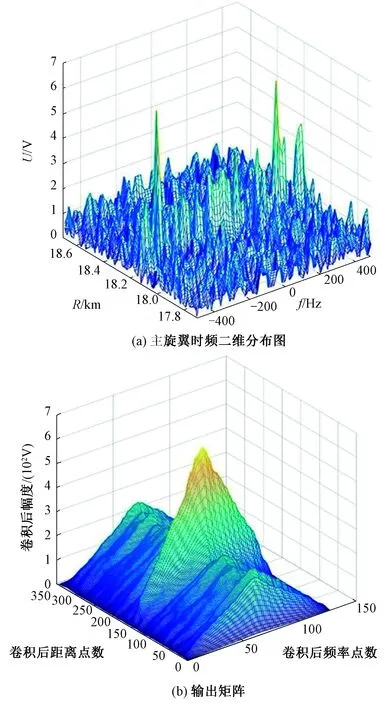
图12 直升机主旋翼回波经过卷积神经网络后的输出矩阵Fig.12 Output matrix of helicopter main rotor echo after convolution neural network

当卷积核与其他类型作目标卷积处理后，输出的二维矩阵将呈现不同的形状。点目标回波经过卷积神经网络后的输出矩阵如图13所示。若目标为点目标(如孤立角反射体)，则二维卷积处理后将在频率维呈现类似矩形形状。

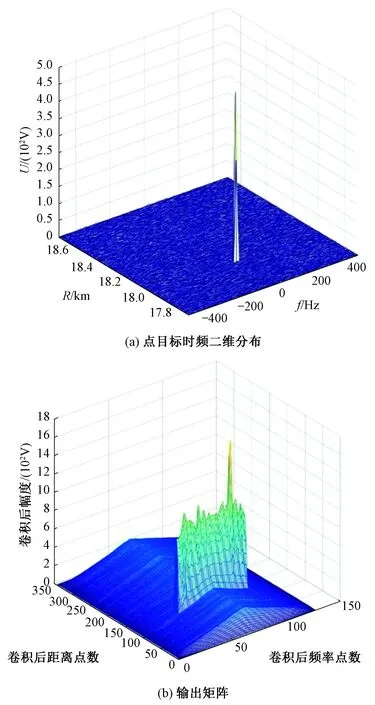
图13 点目标回波经过卷积神经网络后的输出矩阵Fig.13 Output matrix of point target echo after convolution neural network

体目标回波经过卷积神经网络后的输出矩阵如图14所示。由图可知，若目标为体目标(如船只、岛屿等)，则二维卷积处理后的将呈现立方体形状，与主旋翼输出有明显区别。

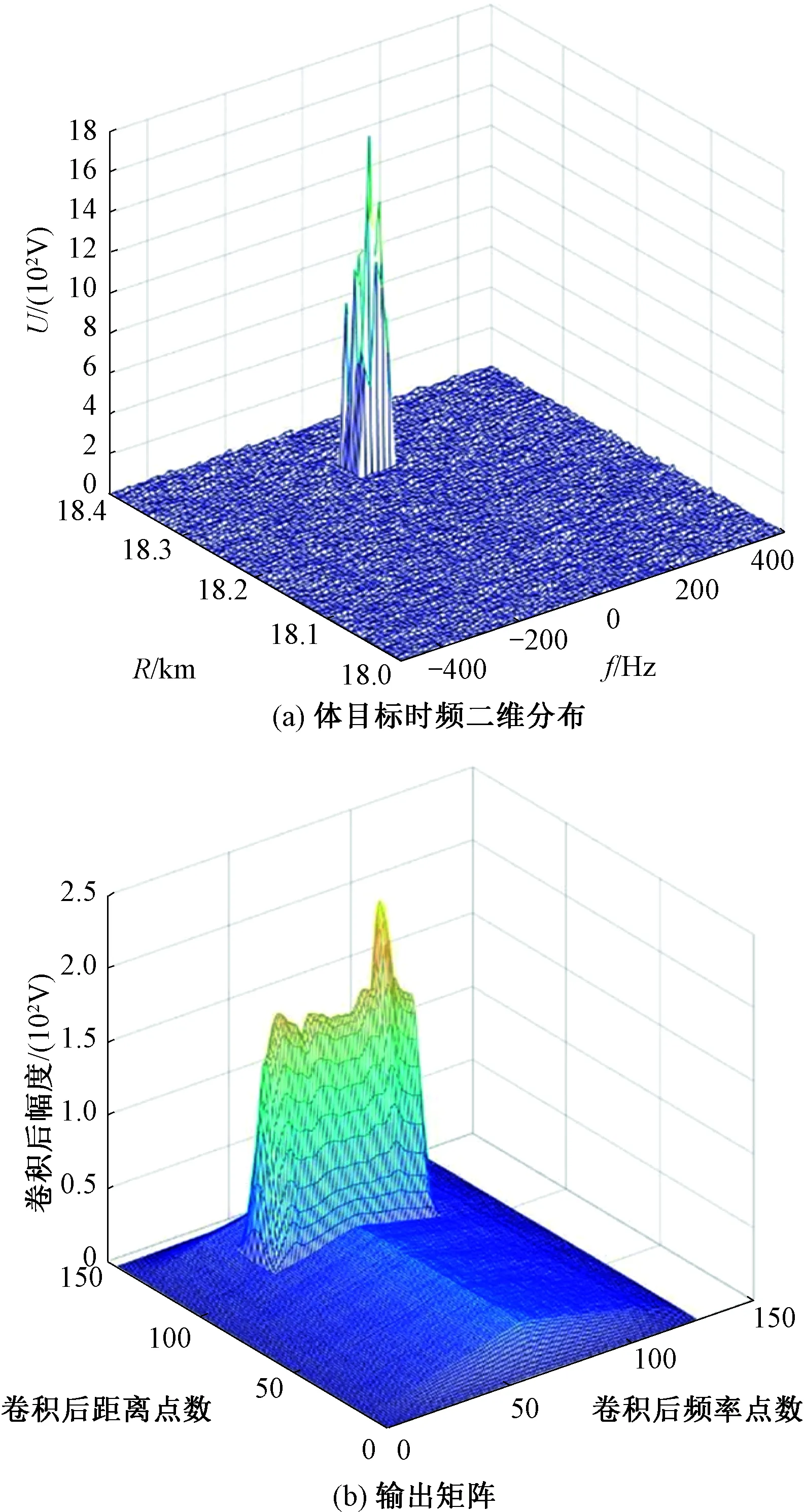
图14 体目标回波经过卷积神经网络后的输出矩阵Fig.14 Output matrix of body target echo after convolution neural network

利用经过卷积神经网络后的输出差异性，可以有效识别直升机主旋翼。直升机回波经过卷积神经网络后，其最大值在距离维上的位置即为直升机主旋翼回波位置。映射到原雷达回波时频分布图上，可获得直升机主旋翼的距离值与频率值。

3.5 识别结果统计分析

采用卷积神经网络技术方法，基于俯仰角为0°的4 000组实测的直升机回波数据，测试并验证基于真实数据的直升机主旋翼识别能力。实测数据参数设置如下：工作重复频率fr=2 kHz，带宽B=10 MHz，积累数为64，直升机运动状态包括悬停、远离、接近等。根据表1统计可得，该方法对直升机主旋翼的识别概率能达到86.2%，识别为其他目标的概率为13.8%。未能准确识别直升机主旋翼的原因有：一是直升机主旋翼回波能量较小；二是主旋翼回波在某些运动状态下会被直升机机体遮挡。若雷达系统能够很好地收到主旋翼回波，则识别概率将进一步提高。

表1 直升机主旋翼识别次数统计Tab.1 Statistics of helicopter main rotor identification times

4 结束语

本文阐述了卷积神经网络中的卷积核概念，仿真分析了直升机主旋翼回波特性，并与实测数据回波时频二维特性进行对比。雷达在LPRF工作条件下，直升机主旋翼回波在频谱的扩展特性可作为识别特征。利用实测直升机主旋翼数据训练神经网络卷积核，将卷积核在实测回波的时频分布图上完成二维卷积与识别处理，正确识别概率超过85%，具有较高的识别概率。后续将深入研究数据训练方法，优化卷积核矩阵，进一步提高目标识别概率。