基于深度卷积网络的雷达辐射源信号识别*

金秋,王宏艳,延淼

(航天工程大学,北京 101406)

0 引言

雷达辐射源识别(radar emitter identification/recognition，REI/RER)技术是电子战领域重要的研究内容，其技术水平制约着整个雷达对抗系统的发展。现代雷达迅速发展，新体制雷达越来越多，电磁环境日益复杂，辐射源交错程度高，信号密度大，已达到每秒数百万脉冲[1]。“高大且杂”的电磁环境为雷达辐射源信号(radar emitter signal，RES)的有效识别带来了很多困难。目前的雷达辐射源信号的识别包括特征匹配法、脉内分析法、数据融合法以及神经网络方法，都停留在辐射源信号特征的表层，没有充分利用辐射源信号的调制特征。文献[2]研究了用图像处理技术处理时频分析图，表征了时频特征具有很好的应用价值。文献[3]将K最近邻(K-nearest neighbor，KNN)分类算法用于雷达辐射源信号的时频特征分类，在高于2.5 dB时可较高的识别率，但在信噪比限制和准确率上还有一定的研究空间。本文提出雷达辐射源信号时频特征与深度网络相结合的方法，构造基于深度卷积网路与时频特征的RES识别模型，实现一种低信噪比、高识别率的雷达辐射源识别新方法。

1 VGGNet

1.1 VGGNet结构

VGGNet由牛津大学计算机视觉组(visual geometry group，VGG)和Google Deep Mind公司一起研发，是当前较为常用的一种卷积神经网络(convolutional neural networks，CNN)。VGGNet[4]的结构包括卷积层、池化层和激活函数，其中卷积层指利用卷积核对输入数据集进行特征筛选处理，可以采用Full卷积，Same卷积和Valid卷积。若输入为x∈Rn，且卷积滤波器w∈Rm，则Valid卷积可以表示为

(1)

式中：t=1,2,…,n-m+1，n>m。Valid卷积不对输入补零。一般来说，卷积流中常用的是Valid卷积。

采用卷积操作能够约减权值连接，引入稀疏或局部连接，以此带来的权值共享策略能够极大的减少参数数目，同时增加数据量，从而避免深度网络出现过拟合现象。且卷积操作具有平移不变特性[5]，所以能够使筛选的特征保留原有拓扑，并且具有很强的鲁棒性。

池化操作则是对特征类型和空间的聚合[6]，降低特征空间维度，可以减少运算量并刻画卷积层输出特征的平移不变特性，减少下一层数据输入维度，进而有效减少下一层的输入参数及计算量，有效控制网络的过拟合风险。池化操作最常用的形式，如图1为最大池化，若池化的窗口大小为k，则池化后参数个数会减少k倍。

激活函数是在深度网络中加入的一种非线性操作，通过层级间的非线性映射使得整个网络的非线性刻画能力得以提升。常用的激活函数有：修正线性单元(rectified linear unit,ReLU)[7]、Softmax函数[8]、Softplus函数(ReLU的光滑逼近)、Sigmoid系(包括Logistic-Sigmoid函数和Tanh-Sigmoid函数等)。

1.2 VGGNet参数设置

VGGNet从Alex-net[9]发展而来,不同的是卷积层主要使用3×3的小卷积核和2×2的小池化核。本文使用VGGNet的16层网络[10]，共有13个卷积层，3个全连接层。所有卷积层有相同的配置，步长为1，维度由64，128，256，到512；共有5个最大池化层，大小为2×2，步长为2；共有3个全连接层，其中前2层是1×4 096通道，第3层是一个1×1 000的特征层。整体结构图如图2所示。

图2 VGG-16参数结构图Fig.2 VGG-16 parameter structure diagram

2 雷达辐射源信号的时频分布

根据雷达辐射源信号时频分析所使用的二维联合分布函数的具体形式的不同，将时频分析方法分为2类，即线性时频表示和双线性时频表示。双线性时频表示也称作二次型时频表示，反映的是信号能量的时频分布。该分布不具有线性可叠加性。二次型时频表示主要有Cohen类时频分布(如伪Wigner-Ville分布、平滑伪Wigner-Ville分布、Choi-Williams分布等)和仿射类(Affine)双线性时频分布(如尺度图、乘积核分布等)。

本文选取部分Cohen类时频分布(平滑伪Wigner-Ville分布[11]、Choi-Williams时频分布[12]和Bord-Jondan时频分布[13])构造RES时频分布训练集。对于信号x(t)，其Cohen类时频分布的表达式定义为

Cx(t,f)=

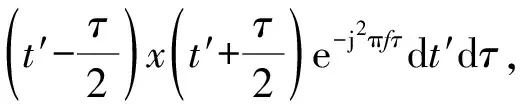
(2)

式中：φ(t-t′,τ)是核函数，核函数不同，分布就不同。核函数的作用是减少时频分析中的交叉项,其选取对时频分布的性质有重要影响。

2.1 平滑伪Wigner-Ville分布(smooth pseudo wigner-ville distribution，SPWVD)

(3)

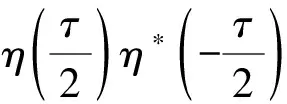
2.2 Choi-Williams时频分布

(4)

式中：σ为尺度因子，决定交叉项的抑制程度和时频分辨率，取值一般在0.1～10之间，如果取无穷大，那么时频分布就变成了WVD。当σ取值越大时，时频分布的分辨率就越高，对时频分布的交叉项抑制程度就越低；当σ取值越小，反之。

2.3 Bord-Jondan时频分布

(5)

该分布的特性是使时频域产生混合联系，一般作为其他分布推到的基础。

3 雷达辐射源信号VGGNet-时频分布分类识别模型

在对雷达辐射源信号进行分类时，先利用时频分析方法提取辐射源信号时频二维联合特征，生成数据矩阵，并通过灰度化处理产生灰度化数据矩阵。灰度化的5数据矩阵以灰度图像的形式呈现，并通过编号产生数据集。将生成的大量数据集分为训练集和测试集，训练VGG16网络，训练后的网络即可用来对未知信号进行分类。

未知信号通过采样和时频变换的运算得到时频二维联合分布灰度图[15]，导入已经训练完成并保存的网络中，经过对信号时频灰度图的分析，即可给出分类的类型，并给出是该类型的可信度(0～1，0表示不可信，1表示绝对可信)。其模型结构如图3所示。

图3 雷达辐射源信号VGGNet-时频分布分类识别模型Fig.3 Classification and recognition model of radar emitter signal VGGNet-time frequency distribution

4 仿真实验及分析

为验证上述模型对复杂体制雷达辐射源信号特征分类的有效性和准确性，选取5种典型的雷达辐射源信号，从-3～16 dB的信噪比下，每个分贝值生成3个时频二维联合特征灰度图像构造成数据集，格式为uint8_656*875，共300幅图像。雷达辐射源信号的调制参数,如表1所示。

生成数据库中雷达辐射源信号0 dB时频灰度图，如图4～8所示。图4～8中a)，b)，c)即为数据库中0dB信噪比条件下对应信号的Bord-Jondan时频分布、ChoiWilliams时频分布和平滑伪Wigner-Ville分布。总而言之，信号的时频二维特征结构信息在3种分布中基本不变，而交叉项在灰度图像上分布差异却很大，可以看作是灰度图存在的噪声。

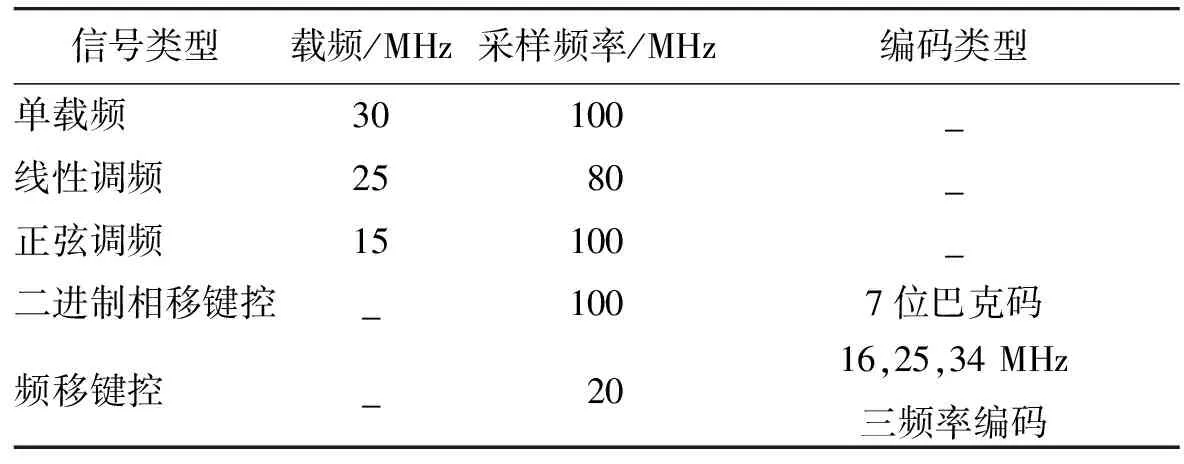
表1 雷达辐射源信号调制参数表Table 1 Radar emitter signal modulation parameter table

图4 单载频信号时频灰度图Fig.4 Time frequency grayscale map of single carrier frequency signal

图5 线性调频信号时频灰度图Fig.5 Time frequency grayscale map of LFM signal

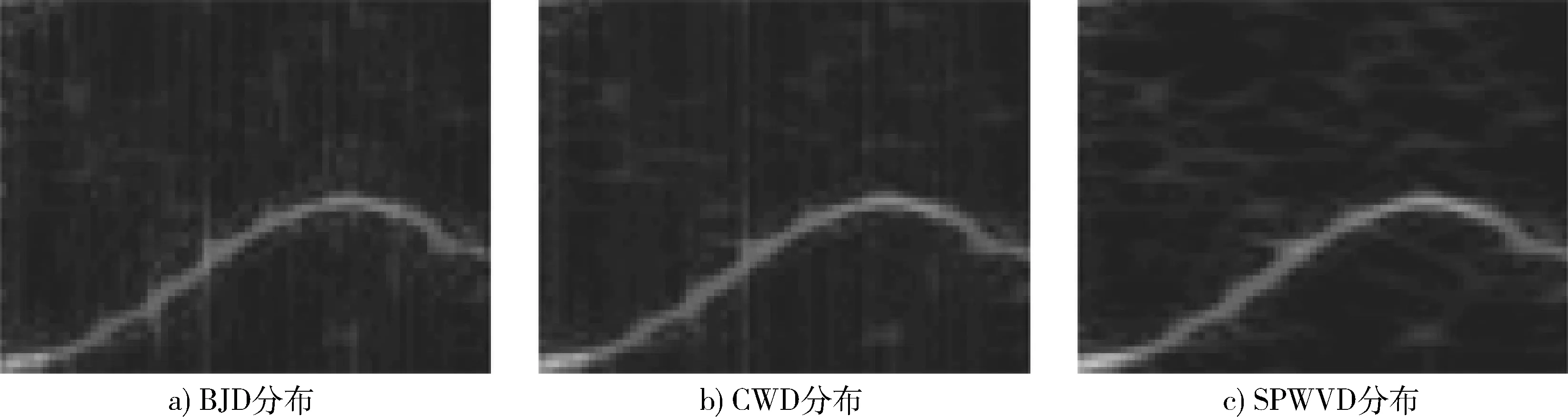
图6 正弦调频信号时频灰度图Fig.6 Time frequency grayscale map of sinusoidal frequency modulation signal

在构造的数据集中，选取90%的数据集为训练集，10%的数据集为测试集，VGG16基本参数设置为：Batch size设置为256；迭代次数为5；Learning Rate：0.001；Weight Decay：0.000 5；Momentum：0.9;

训练模式：CPU

训练过程如图9所示(其中，train为训练集，val为测试集)。

由图9 a),b)可知，train和val的走势皆为趋于变小，第3次迭代后损失函数和top1err几乎为0，说明VGG16在训练至第3代时已经收敛。由图9 c)可知，选取的数据集的拟合难度相对较小，表明了时频灰度图像数据集作为深度网络学习的特征集，以实现RES分类识别的可行性。(top1err和top5err分别指从数据集中抽取1次和5次所预测的错误率，是国际上检验深度网络训练成效的2个常用标准。)

图7 二进制相移键控时频灰度图Fig.7 Time frequency grayscale graph of binary phase shift keying

图8 频移键控信号时频灰度图Fig.8 Time frequency grayscale graph of frequency shift keying signal

图9 深度网络5次迭代曲线图Fig.9 5 Iteration graph of deep network

经测试，本文使用模型在信噪比为-3 dB以上(不含-3 dB)的条件下识别准确率为100%，-3 dB条件下为99.90%，准确度下降原因是因为BPSK信号发生了误判。本文结果与其他文献在同等初始值和信噪比条件下结果对比如表2所示。

表2 实验结果及分析Table 2 Experimental results and analysis (%)

由表2可知，单载频、线性调频以及正弦调频的时频二维特征结构较为稳定，受到干扰后的基本结构趋势还有保留，而二进制相移键控和移频键控信号结构相对较为复杂，在信噪比趋于更小时，受到噪声干扰后交叉项和干扰增多，信号的二维时频特征结构受到破坏，更容易被误判。

5 结束语

时频分析是信号脉内调制特征中较为突出的特征，在复杂电磁环境下，充分利用这一特征实现RES识别具有很大优势。深度卷积网络在图像识别领域取得了良好的效果，本文借鉴其成果应用于雷达辐射源识别领域也证明是可行和有效的。但仿真实验表明，当信噪比降低到-5 dB以下，雷达辐射源信号时频灰度图中的二维联合特征结构会受到噪声干扰而出现断裂、零散的情况，这就使得深度卷积网络参数拟合出现波动。如何实现更低信噪比条件下高精准度的识别和分类，需要进一步加深网络结构、调整网络初始设置，并寻求新的特征以代替时频二维特征。