基于线性非线性回归分析的防空导弹费用建模*

赵曰强，安实，麦强，于道林，张耀东

(1.哈尔滨工业大学 管理学院，黑龙江 哈尔滨 150001；2.中国航天科工防御技术研究院，北京 100854；3.北京电子工程总体研究所，北京 100854)

0 引言

研究防空导弹武器系统费用时，导弹的生产费用单价最受关注。这是因为在武器系统中导弹的技术性能指标可比性强，而地面系统由于使用要求不同，配置繁简差别显著，费用的统计测算离散很大；从整个寿命周期费用来看，生产费用最稳定，研制阶段由于受到技术基础、研制周期、试验鉴定次数的影响费用离散很大；另外，现实中很多防空导弹武器系统的研制生产，一般将导弹和雷达制导等地面系统由不同的承包商分开承担，导弹相对独立性强。综上所述，从导弹的生产费用单价入手易于得到可靠的费用模型。

1 费用变量的分析与选择

费用变量是指影响导弹费用的敏感量[1]。防空导弹武器系统性能指标较多，各指标对费用都有一定的影响，相互间还存在着复杂的关联性[2]。下面对主要技术性能参数进行相关性分析与选择。

首先分析导弹杀伤空域对费用的影响。一般来说在有效载荷(一般指战斗部)给定的情况下，射程增大往往造成发射质量增大，进而引起费用的增加。另外，在射程一定的情况下，提高推进剂的性能虽然可以降低导弹发射质量，但推进剂的费用必定随着增大。提高制导精度可以降低有效载荷，进而大幅降低发射质量，但制导系统的成本会大幅度提升，这在一定程度上会抵消导弹发射质量降低带来的好处。可以看出，在一定制导体制下，射程是影响费用的主要因素。

然后分析导弹质量对费用的影响。发射质量决定了导弹的大小，从而也决定了所需的动力消耗。发射质量越大，费用越大；战斗部质量决定了导弹的杀伤威力，在炸药类型相同的情况下，威力增大，战斗部质量增大，对制导精度的要求降低。可以看出，战斗部质量的变化将从导弹质量和制导精度2个方面影响导弹的费用，其对经费的影响不是单一的增减关系。

此外分析导弹飞行速度对费用的影响。导弹飞行速度增大，可缩短射击周期，提高火力密度，增大有效发射区和杀伤区。同时，导弹飞行速度的提高对导弹控制能力、结构、防热水平等都提出了更高的要求，进而导致导弹费用的增加。

导弹杀伤概率直接取决于导弹的制导精度、引战配合和杀伤威力。其中，制导精度对导弹杀伤概率的影响至关重要。

导弹的可靠性和维修性相关费用可以按导弹武器系统总费用的一定比例来概算[3]。

通过以上分析，结合对导弹武器系统费用敏感的几个主要参数(杀伤空域、导弹质量、飞行速度、战斗部质量、制导精度、目标通道等)，选取以下参数作为研究影响导弹单价的自变量：最大射程、发射质量、最大飞行速度、战斗部质量以及制导误差。

在较早的模型中，自变量多选用发射质量、发动机装药、战斗部质量、最大射程等组合[4-5]。这是由于20世纪80年代以前的防空导弹多是第1代、第2代的产品，技术水平接近，例如：均采用指令制导、脉冲多普勒雷达。后来随着技术的发展，出现了相控阵雷达，防空导弹可以打击多目标。于是出现了以最大射程和多目标数作为自变量的组合。但是现今的导弹制导控制技术得到了大幅度的提升，TVM制导、主动雷达末制导、光学制导和使用直接力控制使得制导精度越来越高，甚至具备了直接碰撞的能力。所以传统的变量参数(如战斗部质量mz)已经难以包含影响导弹费用的全部主要因素；因此，本文引入了新的变量制导误差ρ。另外，多目标能力在全系统费用的估算中将是关键因素之一，系统费用建模时要予以关注[6]。

2 导弹生产费用单价的线性建模

关于防空导弹的生产费用单价和性能参数，数据来源较多，数据的可信度较高，因此可采用参数法。具体而言，首先从已经选出的有代表性的性能参数中确定对导弹费用敏感的自变量，例如：最大射程R，发射质量m，导弹最大飞行速度vm以及导弹制导误差ρ。然后，收集整理类似其他项目的历史数据。最后利用统计回归分析技术建立起费用与自变量间的关系。

假定导弹生产费用单价y(Cmp)与各参数x1～4(R，m，vm，ρ)之间具有如下的线性函数关系：

y=b0+b1x1+b2x2+b3x3+b4x4+e，

(1)

式中：e为服从独立正态的随机变量。

运用多元线性回归分析来确定式(1)中的待定参数b0，b1，b2，b3，b4。

可见对x1～4(R，m，vm，ρ)的n组不同取值(R1，m0，vm1，ρ1)，(R2，m2，vm2，ρ2)，…，(Rn，mn，vmn，ρn)；有对应的y(Cmp)的值Cmp1，Cmp2，…，Cmpn。

(2)

式中：X为自变量矩阵；Y为因变量；B为回归系数；E为随机误差，由式(1)得

Y=XB+BE，

(3)

(4)

变换得

(5)

假定(X′X)的逆矩阵(X′X)-1存在，则得到式(5)回归问题的最小二乘解为

(6)

2.1 大中型导弹生产费用单价线性模型的建立

建模用到的样本数据真实有效性是取得良好统计结果的关键，参照文献[7-11]等，查找分析几个国内外最新防空导弹型号的性能参数和费用数据，并参照美国国防部公布的陆军紧缩指数，对于不同时间价格水平进行比较，整理列于表1中。

由表1中导弹主要性能技术参数作为自变量x1～4(R，m，vm，ρ)，导弹生产费用单价y(Cmp)作为因变量，进行多元线性回归分析，运用Matlab运算得：

表1 几种防空导弹费用数据

注：Cmp为折算的2010年数据，单位人民币万元

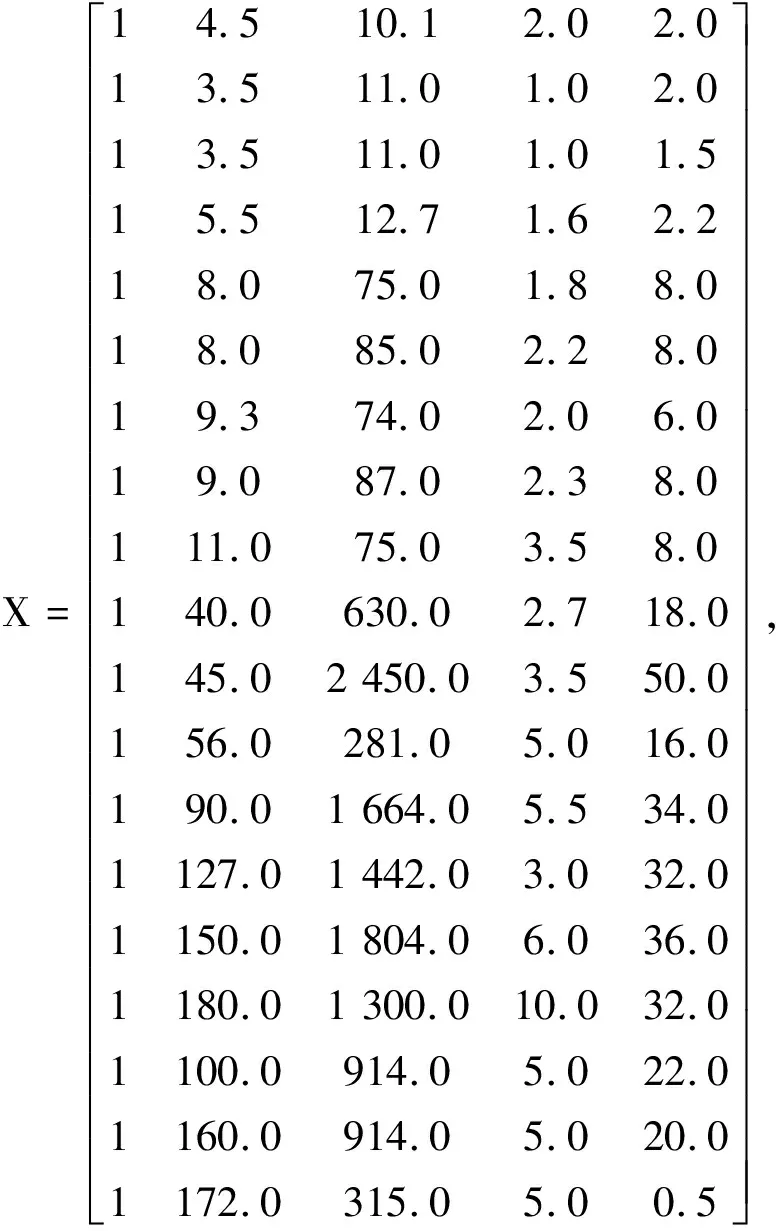
Y= (45.0，49.5，55.6，930.0，157.5，190.0，229.3，

192.5，264.0，316.0，250.0，430.0，690.0，885.0，

856.0，865.0，1 035.0，1 620.0，1 500.0)T.

(7)

将式(7)代入式(2)，得

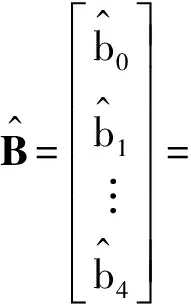
(8)

代入式(1)，则得回归费用模型：

y= 61.940 2+6.362 1x1-0.126 8x2+

52.780 6x3-13.426 3x4.

(9)

首先利用表1样本值和计算值对模型进行验证，由式(9)得出计算值和历史数据值进行比较可以看出，小型导弹的费用估算偏差较大，最大到了279.02%，该模型已经不能适用；该模型对大中型导弹的适用性略好。

这里，解决模型对小型导弹和中大型导弹拟合结果偏离的问题，美国陆军导弹系统全寿命费用模型中对于研制费用提供了3个CER解析式，其中第一个只能适用于便携导弹的费用估计[12-13]。这也得到一些提示，可以对小型和大中型导弹的费用估计进行分段处理。通过对导弹数据的分析，选用导弹发射质量30 kg作为分段点。

先来看发射质量大于30 kg的导弹费用的估计。将表1中序号5～19导弹发射质量大于30 kg的导弹主要性能技术参数作为自变量，进行多元线性回归，则得大中型导弹的回归费用模型：

y= 192.866 9+5.483 0x1+0.369 2x2+

61.753 7x3-27.243 9x4，m>30 kg.

(10)

同样先利用样本值和计算值对模型进行验证，由式(10)得出计算值，和样本值对比看出，对于大中型导弹通过多元线性回归得到的导弹生产单价的费用估算模型并由此而得到的计算值和历史数据(样本值)吻合的较好，有一半的数据偏差在5%以内，最大的偏差仅为21%。

我们进一步对模型的多元回归进行方差分析，分析结果见表2。

表2 多元线性回归的方差分析Table 2 Variance analysis of multivariatelinear regression

相关系数值为

R2=3 167 900/3 261 700=0.971 3.

(11)

调整相关系数值为

Ra2=1-9 376.3/(3 261 700/14)=0.959 8.

(12)

可见有超过95%的费用发生是由选定的4个变量(R，m，vm，ρ)决定的。

Ra2和R2数值差别不大，没有出现Ra2数值远小于R2的情况，说明参数选择数量合理。

查F分布表可得F4，10(0.01)=5.99<84.465 5(统计量F的值)，同时检验的概率P<0.01，所以，假设H0：b1=b2=b3=b4=0不成立，回归方程通过了显著性检验，即认为所得的线性回归方程有意义。

2.2 小型导弹生产费用单价线性模型的建立

现在将几种发射质量小于30 kg的导弹生产单价和主要性能技术参数整理见表3。

从对表2中的数据分析可以看出，小型便携导弹制导体制相近，制导精度相当，导弹生产单价和作战空域、速度以及战斗部质量关联不大，而和导弹的发射质量关联显著，通过各种参数组合为自变量的回归及方差分析也可以说明这一点。

将表3中导弹发射质量作为自变量，导弹生产单价作为因变量，进行线性回归，得小型导弹的回归费用模型：

y=-7.489 0+5.564 7x2，m≤30 kg.

(13)

同样先利用样本值和计算值对模型进行验证，由式(13)得出计算值，和样本值对比看出，由导弹生产单价的费用估算模型得到的计算值和历史数据(样本值)最大偏离13%，偏差不大。

进一步对回归模型进行方差分析，见表4。

对α=0.05，查F分布表可得F1，6(0.05)=5.99。

因为F>F1，6(α)，同时，p=0.026 2<0.05，线性回归方程反映了导弹生产单价和导弹发射质量的相关关系。

2.3 导弹生产费用单价多元线性回归模型

根据上面的计算和仿真，以导弹发射质量30 kg为分界线建立分段函数，建立起导弹的生产费用单价y(Cmp)的线性模型。

(14)

式中：y(Cmp)为导弹的生产费用单价，万元(人民币)；x1(R)为导弹的发射质量，kg；x2(m)为导弹的最大射程，km；x3(vm)为导弹飞行的最高Ma；x4(ρ)为导弹制导误差，m。

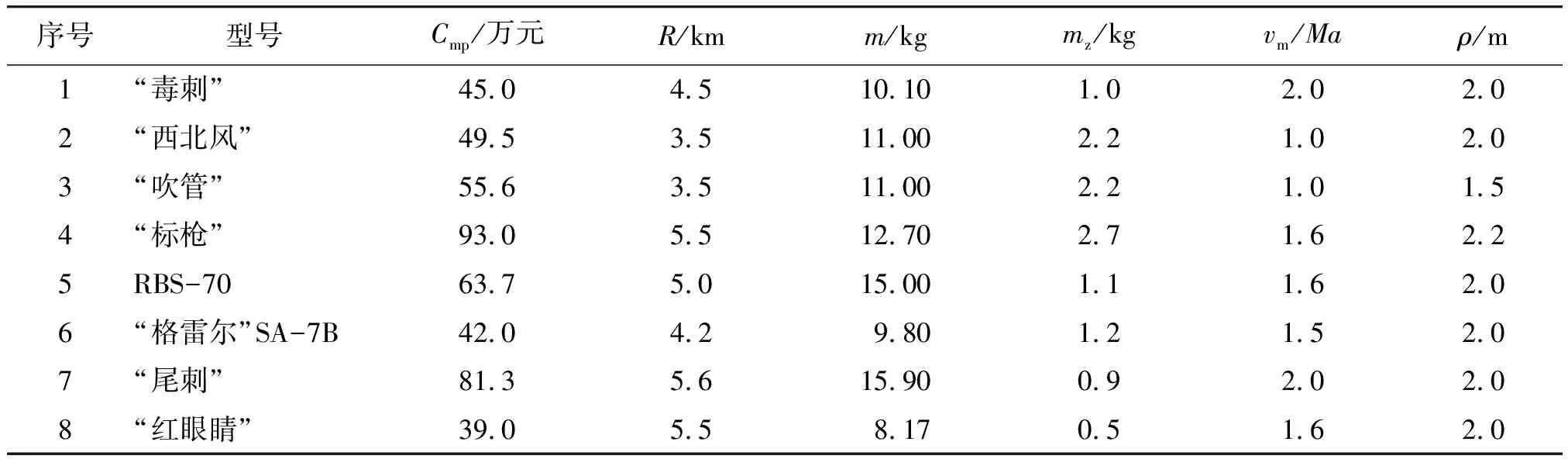
表3 几种小型防空导弹费用数据Table 3 Cost data of several small air defense missiles

注：表中Cmp为折算的2010年数据，单位人民币万元。

表4 小型导弹多元线性回归的方差分析Table 4 Variance analysis of multivariate linearregression for small missile

3 导弹生产费用单价的非线性建模

上节建立起了导弹的生产费用单价与特性参数之间的线性函数关系。采用了对小型和大中型导弹的费用估计进行分段处理，取得了理想的结果。下面进一步开展非线性分析，建立非线性回归模型，来探求比较形成最佳的解决方案[14]。

基本原理是非线性回归最小二乘拟合[15]。利用Matlab非线性曲线拟合命令nlinfit函数，进行非线性函数的系数用最小二乘法估计，该函数使用高斯—牛顿算法，调用格式为

beta=nlinfit(X,y,@myfun,beta0).

(15)

式中：y为因变量矢量；X为自变量组成的矩阵；beta0为包含系数初始值的矢量；@myfun参数为一函数，具有以下的形式

yhat=myfun(beta,X)，

(16)

式中：beta为系数矢量；X为自变量矩阵；@myfun为参数返回一个拟合y值的yhat矢量。

3.1 建立二次函数模型

设定y(Cmp)与各参数x1～5(R，m，mz，vm，ρ)之间具有如下的函数关系：

y= beta1x1+beta2x2+beta3x3+beta4x4+beta5x5+

beta6x12+beta7x1x2+beta8x1x3+beta9x1x4+

beta10x1x5+beta11x22+beta12x2x3+beta13x2x4+

beta14x2x5+beta15x32+beta16x3x4+beta17x3x5+

beta18x42+beta19x4x5+beta20x52.

(17)

这里构建的是含有平方项和交互项的二次函数表达式。

调用Matlab中nlinfit函数进行估算，得到beta为系数矢量，beta(20)为极小值，且超出置信区间略去，即得到最终的多元二次非线性回归的解析式：

y= -221.64x1-49.448x2+609.5x3+168.38x4-

144.07x5-0.1807 5x12-0.249 01x1x2+

0.816 3x1x3+72.346x1x4+3.574 5x1x5-

0.035 167x22-0.269 65x2x3+11.512x2x4+

4.598 9x2x5+10.215x32-192.42x3x4-

60.829x3x5-105.38x42+202.59x4x5，

(18)

式中：y(Cmp)为导弹的生产费用单价，万元(人民币)；x1(R)为导弹的发射质量，kg；x2(m)为导弹的最大射程，km；x3(mz)为战斗部的质量，kg；x4(vm)为导弹飞行的最高Ma；x5(ρ)为导弹制导误差，m。

对该模型进行回归检验，由命令函数[b,bint,r,rint,stats]=regress(y_result,x)，得检验回归模型的统计量：

stats=(0.959 47，86.075，1.074 4e-9，12 430).

(19)

可见，相关系数平方值R2=0.9594 7说明回归方程显著模型拟合程度较高，F=86.075不超临界，显著性概率P=1.074 4e-9<0.05拒零假设，模型有意义，均方根误差RMSE=12 430。

采用式(18)，利用表1中的导弹费用数据拟合结果为

Y_result= (45，49.5，55.6，93，157.5，190，229.3，

192.5，264，316，250，430，690，885，

856，865，1 035，1 620，1 500).

(20)

将拟合值与样本值进行对比见图1。

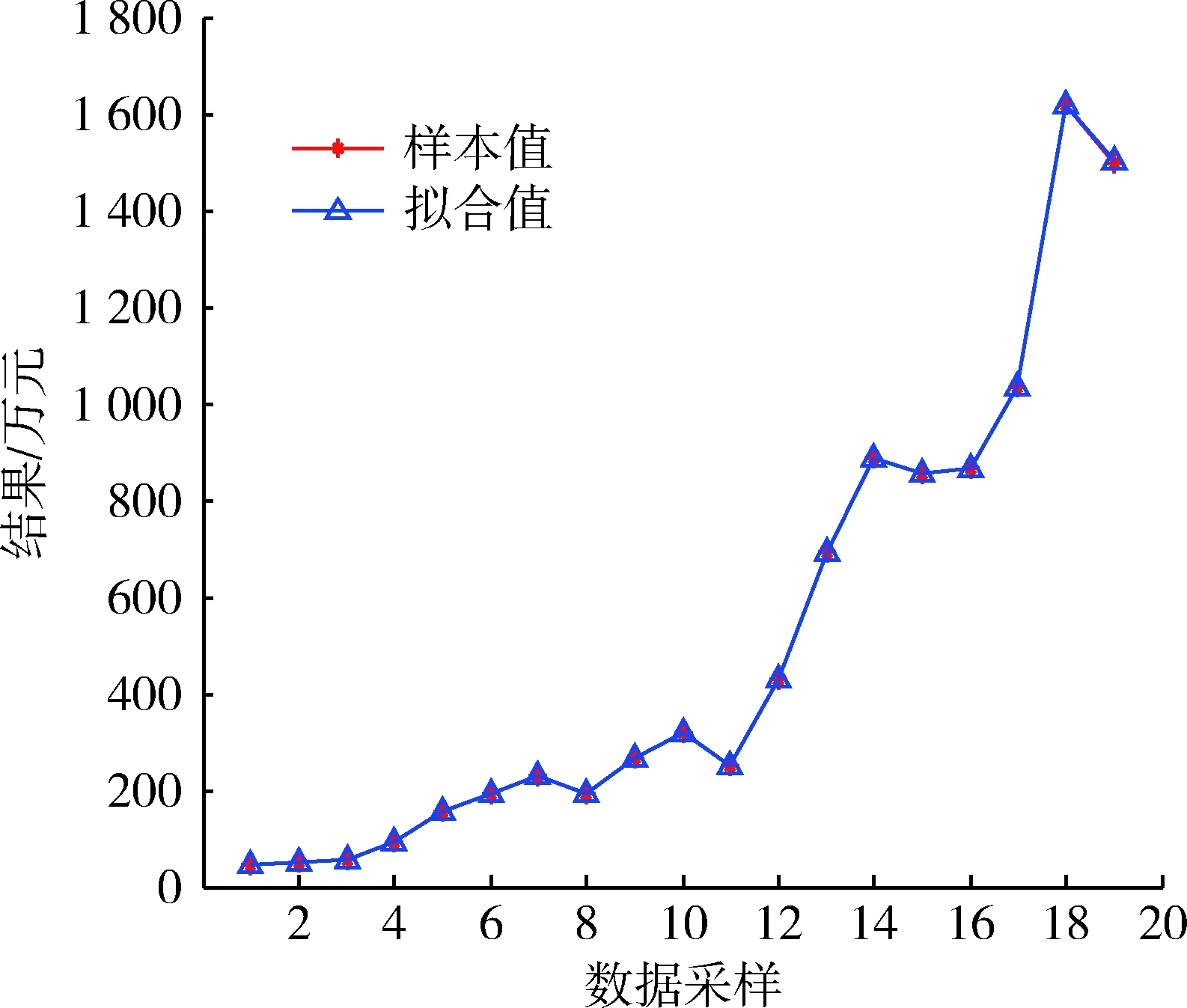
图1 二次函数模型拟合值与样本值对比图Fig.1 Contrast diagram of fitting value and samplevalue of quadratic function model

本模型拟合精度高，用一个解析式较一致地表达了因变量和各参数的关系，而不需要采用分段表示。相对线性回归模型，该模型具有更高的计算复杂性，适合使用计算机进行计算。

3.2 建立非线性函数模型

为了进一步简化允许特定一点出现较大偏差(可视孤立样本予以剔除)的条件下的拟合的函数。先看下每个参数对性能的影响，确定交互项和单一项，然后遍历所有指数的可能，获得和原始数据的最小误差。建立生产费用单价的模型：

y= -71.589+8.692x1-727.39x4- 9.710 4x10.5x30.5+749.1x20.05x40.9，

(21)

式中：y(Cmp)为导弹的生产费用单价，万元(人民币)；x1(R)为导弹的发射质量，kg；x2(m)为导弹的最大射程，km；x3(mz)为战斗部的质量，kg；x4(vm)为导弹飞行的最高Ma。

采用上式，利用表1中的导弹费用数据拟合结果为

Y_result= (61.364，49.017，49.017，73.463，

183.54，193.23，189.77，206.49，228.13，

308.03，281.18，540.08，681.78，911.92，

895 718.29，1 040.4，1 613.6，1 499.2).

(22)

将拟合值与样本值进行对比如图2所示。

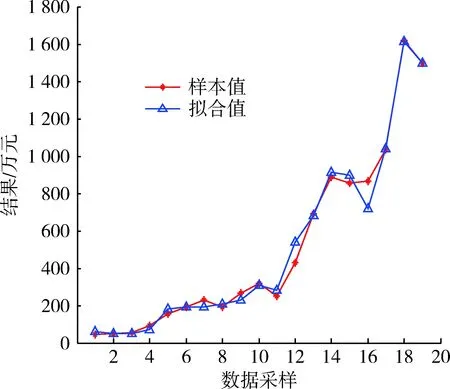
图2 非线性模型拟合值与样本值对比图Fig.2 Contrast diagram of fitting value andsample value of nonlinear model

对该模型进行回归检验，得检验回归模型的统计量

stats=(0.968 53，110.25，2.032 3e-10，9 557.2).

(23)

可见，相关系数平方值R2=0.968 5说明方程回归显著，显著性概率P=2.032 3 e-10<0.05存在非零系数，说明拟合模型有效。

该模型式(21)和原数据总的误差为540，平均每个点的误差为28.4，最大点的误差为150.5。

本模型相对二次函数模型式(18)大为简化，检验有效，但是从图2可知，整体拟合较好，个别点有一定的偏差(17%以内)。

4 结束语

采用线性回归的方法建立导弹生产费用模型式(14)，由于选取的参数典型且与费用相关大，建立的模型相对简单且精度高，易于计算，且物理意义明确，不足之处是要根据导弹的总质量大小分两段进行拟合。非线性回归二次函数建模、非线性建模都取得了很好的结果，避免了线性回归模型分段的不足；但计算略复杂，适合计算机运算。二次函数模型式(18)精度除质量小、近程的个别装备，整体精度较高，但结构复杂，几乎包含了各参数的平方项和交互项；非线性模型式(21)结构简单，精度较好，能用一个式子简明准确地表达了所有防空导弹的生产费用单价。本文建模选取的费用变量虽然相关性较高，但在应用中还应根据工程实际，考虑其他费用变量的作用。