导弹机动路径的差分聚类最优规划*
王凯光,高岳林
(北方民族大学 数学与信息科学学院,宁夏 银川 750021)
0 引言
目前,战时导弹火力打击问题的主要表现为无障碍机车机动路径优化分配研究较多,而含路径威胁的机车机动路径优化研究偏少,模型构造方面,李敏[1]做了基于车载导航系统的路径规划方法研究,邓必年[2]建立了基于蚁群优化算法的物流配送路径规划方案,周慧子[3]等建立了面向自动驾驶的动态路径规划避障算法,李进龙[4]等介绍了基于改进蚁群和免疫算法融合的多配送中心路径优化模型。这些规划模型的建立在整体上仅考虑了导弹本身机动过程,割离实战威胁和路径规划之间的关系,从而忽略了多威胁的实战环境对机动路径的影响,而差分进化算法[5-6]可以对全局环境进行整体寻优,可以利用差分进化算法的全局寻优能力对机动路径进行系统整合。本文在前人研究基础上,结合数字模拟技术刻画发射车在含路径威胁路段的路径轨迹,运用差分聚类分析和Floyd路径算法构建战时含威胁路径的导弹机动路径最优规划的数学模型,弥补无路径威胁条件下路径规划的单一性,提升了导弹在联合指挥作战体系下的安全性、时效性、稳定性、合理性。
1 问题要素描述
针对n(n≤5)个波次的战时打击任务,假设战时导弹类型集合为Ω={甲,乙,丙,…},待打击目标集合为Ψ={A,B,C,…,N},弹目匹配函数映射关系为f:Ω→Ψ,假设第i个转载地域导弹数量为Xi,战时军事物流仓库、战时转载地域、导弹机动发射点、火力待打击目标为Dq(xq,yq),Zi(xi,yi),Fj(xj,yj),Nq(xN,yN),战时作战区域相关要素及其道路分布假设为加权图G=(V,E,μ),V为加权图中的任意一点,E表示图中任意两点间线段,μ表示线段权重,现在假设有k辆发射车,平均部署在战时物流仓库{D1,D2,…,Dq}、转载地域{Z1,Z2,…,Zi}、导弹发射点{Z1,Z2,…,Zj},第n波次对目标进行打击的导弹总数为{An,Bn,Cn,…,Nn}。既要考虑到在含威胁路径上机动的整体暴露时间尽可能短,也要规避敌方的火力侦查和打击,同时要缩短单台发射装置的最长暴露时间,要求整体暴露时间X和单辆发射车最大暴露时间Y尽可能短。
2 聚类分析和Floyd最短路径算法阶段
鉴于路径威胁的不确定性和多变性,采用多层次聚类分析和动态聚类法对含威胁的路径段进行算法研究,首先对含威胁的路径进行多层次化类,提取主要影响因子,运用动态分析法进行归类,在初始状态给出路径数据在可视化环境下的图像分类,随后给出基于某计数原则在化类间重新组合的数据样本。路径规划属于大样本数据的聚类分析,其操作方法是:先粗略分类,后逐渐调整,结合Floyd算法原理进行导弹机动最优路径算法设计。
算法流程如下
Step 1:在控制数据表中输入机动波次、导弹型号与弹目类别匹配函数、导弹数据参量、物流参量以及机动射击点和目标位置Dq(xq,yq),Zi(xi,yi),Fj(xj,yj),N(xN,yN)。
Step 2:输入Floyd算法程序,利用其短距原理计算机动发射点与机动起始点间距。
Step 3:提取所有机动间距中路径长度最短的作为导弹运输路径,一般路径数量为大于等于某一常数m(m为机车数量与物流仓库数量的数量比)。
Step 4:剔除所选的最短间距中的m个机动起始点,同时进行同参数聚类分析,经聚类对照后机动起始点数量小于出发点总数,则返回Step 3,否则进入Step 5。
Step 5:计算最大暴露时长,取所有机动路径中间距最长路径除以机动平均速度即得最大暴露时长,为保证导弹机动的统一性,设置0时刻为机动路径的出发时刻,同时设置最大暴露时长为齐射时刻,齐射时刻与出发时刻的时长正向差值为相应路径导弹机车运输时长,然后计算机动节点处的间隔时长。
Step 6:作空集判断,即判断是否存在某2条路径中的机动机车在某一非主干道路径段反向行驶的时长区间为空,若空集成立,则取其较短路径中的机车起始点作为出发起始点并返回Step 6,否则进入Step 7。
Step 7:对导弹打击目标进行纵向排序,分为N个点以保证打击目标不在同一点,同时按照如此次序对k个导弹发射点进行横向排序,将打击目标与导弹发射点按照匹配关系对应为N个区域,N个区域所包含的导弹发射点与目标间距的地面连线为导弹投射间距。
Step 8:对已完成的导弹打击波次进行程序性终止判断,若波次数小于n,则进入Step 9,否则终止算法,同时对所有导弹机动路径以及相应节点时刻进行输出作统计处理。
Step 9:输入Floyd算法程序,计算物流配送中心与导弹发射地点的最短路径及其间距。
Step 10:为方便考虑物流配送与导弹发射点间路径状况,在这里假设任意物流配送与相应导弹发射点间路径数量小于上线数值Xi,同时选取最短路径作为运输路径。
Step 11:剔除Step 10 所选的导弹发射点,对导弹发射点数量进行判断,若小于k,则返回Step 10,否则进入Step 12。
Step 12:对Step 5中的齐射时刻作预处理,即将其作为新一出发点的出发时刻,并计算经过各节点时刻以及到达目标点时刻,同时为保证机车在转载区域时长较短,仍需判断Step 6中的空集情况。
Step 13:对于空集不成立的情况,则顺次延后任一2条路径中较短路径的出发时刻并返回Step 12,否则进入Step 14。
Step 14:判断时刻差值,即判断是否存在导弹发射车到达某一物流配送点的时刻差值小于10 min的情况,若存在,则顺次延后任一2条路径中较短路径的出发时刻,并返回Step 14,否则进入Step 15。
Step 15:将物流配送点作为下一次机车初始点,将前一波次所剩导弹发射点作为机动终点,返回Step 2。
3 差分进化算法阶段
3.1 差分算法一般模型
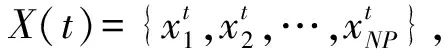
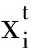
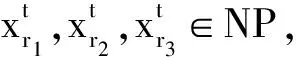
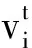
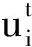
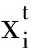
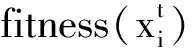
3.2 差分进化算法伪代码

4 数学模型
4.1 模型假设
(1) 作战区域各道路节点及道路交通状况已知,且除主干道可以双向通行之外,其他车道只能单向通行。
(2) 每一辆导弹发射车原则上只能连载1枚导弹,要多波次连射,每个发射点位使用不超过1次,且需要返回导弹转载地域进行实时装弹,各转载地域弹种类型和数量满足需求。
(3) 每辆发射车车速平均设置为50 km/h,每一发射点位只能容纳1台发射装置,各转载地域最多容纳2台发射装置,单台转载作业耗时10 min。
4.2 评价指标
本文拟从安全性、时效性、稳定性、合理性4个方面对战时环境中多波次条件下关于含有路径威胁的导弹机动路径的最优规划问题进行建模和。
(1) 安全性评价指标:导弹运输属于军事物资配送范畴,物资运送时间与机件损耗呈正相关,导弹运输的安全问题应当重视,确保打击任务顺利完成。
(2) 时效性评价指标:导弹战略运输过程最重要的就在于,军事物流的保障能力要紧跟战时变化。在本文所研究的问题中,要求同一波次导弹齐射而且要求整体暴露时间(所有发射装置的暴露之和)最短,由于每一辆导弹发射车的出发时刻均不相同,因此导弹战略运输的时效性就表现为每辆发射车最大暴露时长。
(3) 稳定性评价指标:战时导弹机动路径规划的稳定性主要取决于战时物资运输水平、指令决策、人机调配、机件故障等可控因素。本文研究的问题中,为了使得战时各要素整体暴露时间最短,战时各要素必须稳定在一定的可控范围。
(4) 合理性评价指标:战时火力打击任务分配的合理性主要取决于战时地貌、战时部署、战时结构、作战对象、作战效率、作战意义等[7-8],本文考虑到导弹发射点和待打击目标之间的关系,围绕弹目匹配函数关系f:Ω→Ψ进行合理性研究。
4.3 模型构建
针对n个波次的战时打击任务,可以将其分为奇数个(即2n-1)个阶段,前2个波次分别为待机区域携带导弹沿道路机动到各自指定发射点位实施第1波次导弹机动发射,从第1波次导弹发射点位返回转载地域、从转载地域机动至第2波次导弹发射点位实施第2波次导弹发射,则多目标优化问题可转化为单目标优化问题[7-8],设目标函数为
(1)
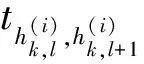
4.3.1 阶段性约束条件
第1阶段
(2)
(3)
(4)
(5)

(6)
(7)
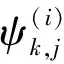
第2阶段
(8)
(9)
(10)
(11)
(12)
(13)
(14)
式(9),(10)分别表示第2阶段起点为第1波次导弹发射点,终点为第1波次导弹转载地域;式(11)表示所列路径的相邻节点2个符合战场实际情况且道路相通;式(12)表示任意单行道节点的反向行驶时间区间交集为φ;式(13)表示在第1阶段存在前提条件下,第k辆车在第2阶段的出发时刻非负;式(14)表示到达任意物资配送中心的导弹发射车数目不大于最大导弹数目Xi;式(15)表示对每一导弹发射车驶离第1次导弹发射点的时间进行调控并使其满足到达同一转载地域的任意2辆导弹发射车的时间差不小于10 min。
第3阶段
(15)
(16)
(17)
(18)
(19)
(20)
(21)
(22)
(23)

4.3.2 算法结果
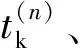
(24)
(25)
(26)
(27)
根据上述模型,我们可以确定打击目标ψ∈{A,B,C,…,N}的位置N(xN,yN)可按纵坐标分为N个区域,每个波次k个发射点的位置Fj(xj,yj)也可以按其纵坐标分为一一对应的N个区域,同时可以确定导弹发射任务的机动方案。
5 算法测试
现有A,B,C3类发射机车,符合模型假设条件,各转载地域弹种类型和数量满足需求。相关道路情况如图1所示(道路节点J01~J62),相应位置坐标由随机函数按照仿真模拟图给出。
5.1 差分聚类算法流程
Step 1:初始化参数:种群规模NP;缩放因子F;变异概率CR;空间维数D;迭代次数T。
(1) 对每个样本Jk,k∈D计算tk,即样本个体到每个机动点的聚类距离;
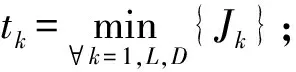
(3) 计算适应度函数值Z(xi)。
Step 4:变异操作、交叉操作按3节流程进行。
Step 6:终止检验:如果达到最大进化代数或满足误差要求,则输出最优质列表;否则转Step 3。
5.2 问题求解
对问题所描述的两个火力打击波次进行系统性分析,种群规模NP为60,变异因子和交叉概率分别为0.5和0.1,进化代数选择为不超过最优值得最大进化代数。从变量参数选择上属于多目标优化问题,因此可以转化为单目标优化问题,设目标函数为
(28)
根据前面2个阶段的算法分析及其数学模型的建立,将表1中数据及相关参数代入公式,通过TerrainView-Lite地理仿真模拟[9-11]对含威胁路径进行可视化模拟仿真,含威胁路径仿真模拟结果如图1所示,含威胁路径段的阶段性规避演化如图2所示,再利用差分聚类算法法和Floyd最短路径路径算法[12-17],通过Matlab编程进行求解,最终得到路径规划的最优分配方案,表1给出了第1波次12辆导弹发射车在含有威胁路径机动规划中的最优分配方案。
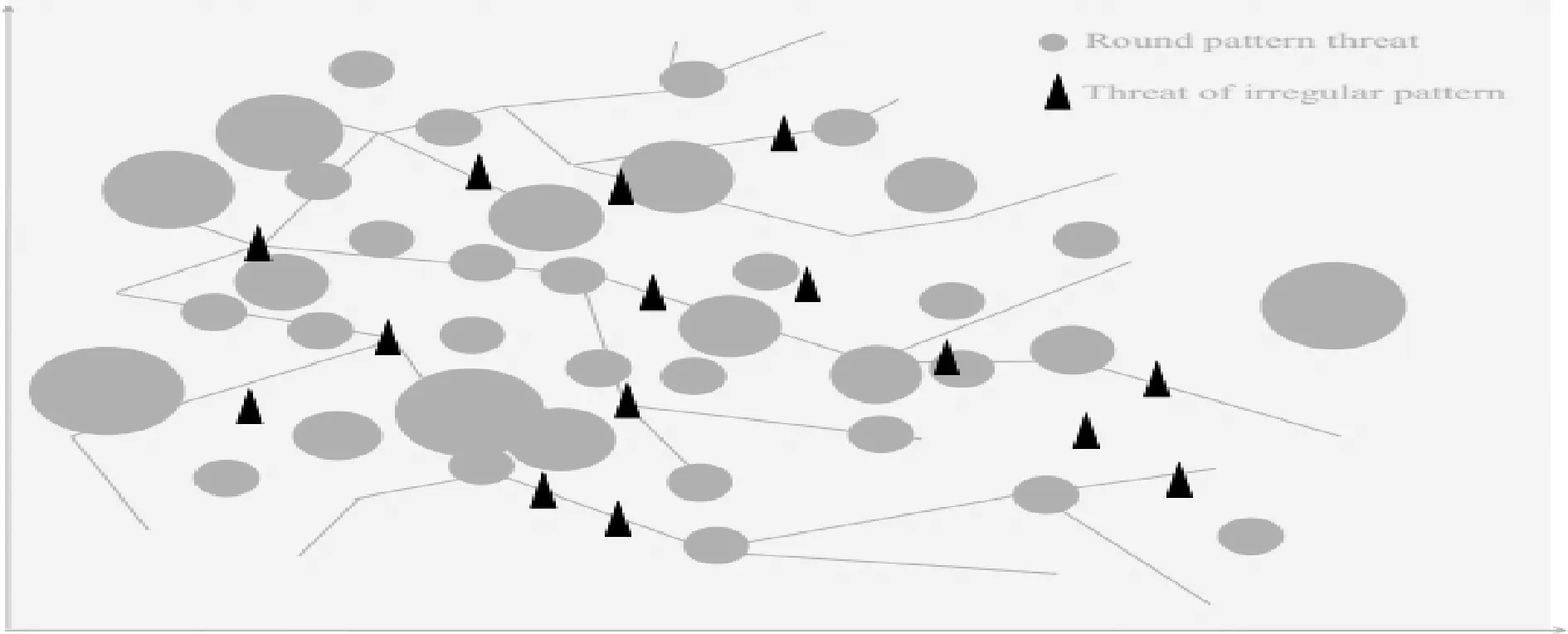
图1 TerrainView-Lite地理仿真模拟图Fig.1 Terrain analogue simulation by Terran View-Lite

图2 3个联合作战方案关于一级评价指标SI1的优度Fig.2 Superiority of the three joint operations plan on thefirst level evaluation index SI1
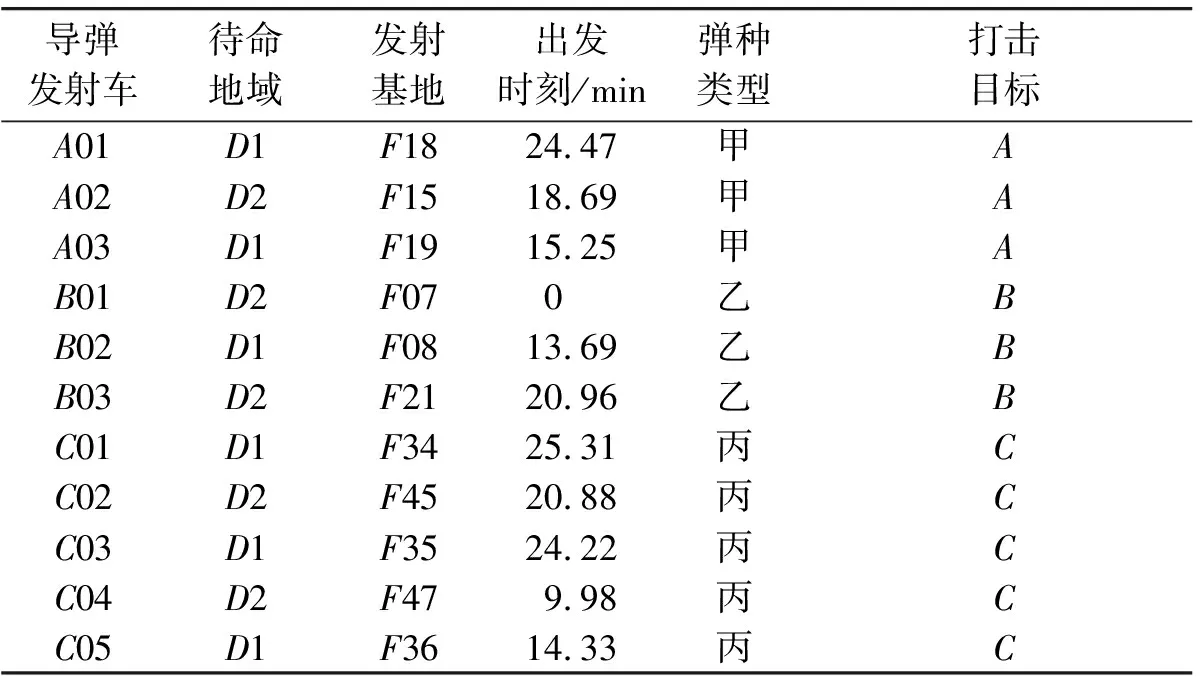
导弹发射车待命地域发射基地出发时刻/min弹种类型打击目标A01D1F1824.47甲AA02D2F1518.69甲AA03D1F1915.25甲AB01D2F070乙BB02D1F0813.69乙BB03D2F2120.96乙BC01D1F3425.31丙CC02D2F4520.88丙CC03D1F3524.22丙CC04D2F479.98丙CC05D1F3614.33丙C
6 结束语
本文对战时多波次导弹火力打击任务条件下含威胁路径的导弹机动路径的规划方案的问题进行了系统研究,采集相关数据,运用TerrainView-Lite地理仿真技术进行含威胁路径的可视化模拟,在算法方面,分析了含威胁路径规避算法阶段、Floyd最短路径算法阶段这2个算法阶段,利用差分聚类算法从系统性角度建立了战时导弹火力打击任务在含有威胁路径的机动规划的数学模型,从合理性、稳定性、时效性、安全性4个方面的指标进行了分析评价。最后通过算法实例对文中所涉及到的数学模型进行测试,结果表明,该数学模型能够较好求解出含路径威胁的导弹机动路径最优规划问题。

