泡沫增阻法清除空间碎片的喷射误差分析*

李人杰，向开恒，陈杨

(航天科工空间工程发展有限公司，北京 100854)

0 引言

自1957年第1颗人造卫星发射以来，人类已经将数千颗航天器送入地球轨道，其中绝大部分已丧失功能，并由于解体、碰撞等事件，产生了大量的空间碎片。目前，在轨的空间碎片中尺寸大于10 cm的有2万多个；尺寸大于1 cm的超过60万个；尺寸大于1 mm的则有上亿个[1-2]。而且，空间碎片的数量将以每年10%的速度递增[3]。

空间碎片运行速度极快，所以会对航天器和航天员的安全产生巨大的威胁。1 mm的碎片会使航天器的子系统失效，1 cm的碎片会导致整个航天器失效，而10 cm的碎片则会将航天器彻底摧毁[4]。随着空间碎片数量的与日俱增，空间碰撞事件频发，已经严重影响到了人类正常的航天活动[5]。

然而，在自然情况下，空间碎片数量的减少速度远小于其增长速度，因此必须采用一定的技术手段来清除空间碎片。国内外发展了多种技术手段，可分为抓捕清除技术、推移清除技术和增阻清除技术3类[6-7]。泡沫增阻法是一种新的增阻清除技术，通过向空间碎片喷射泡沫，增大碎片所受的大气阻力，使其在规定时间内再入大气层烧毁[8]。该方法不需要空间碎片清除卫星(以下简称卫星)与碎片直接接触，可以在远距离实施，这是一个显著的优点，但同时为了使泡沫能够被精确地喷射到空间碎片上，对卫星和空间碎片的定轨精度提出了较高的要求。

本文分析了使用泡沫增阻法清除空间碎片的特点，建立了该方法实施中的运动学模型与喷射误差计算模型，研究了影响泡沫喷射误差的因素，并针对清除不同大小的空间碎片所允许的喷射误差和卫星轨道误差提出了要求。

1 泡沫增阻法

1.1 基本概念

泡沫增阻法是由欧空局和意大利Pisa大学在2011年提出的一种空间碎片清除方法，属于增阻清除技术[9]。具体工作原理是：卫星通过安装的喷射装置向空间碎片喷射泡沫，泡沫接触并粘附在碎片上，泡沫膨胀为低密度、大体积的球体，碎片的面质比因此增大，进而所受的大气阻力摄动效应增大，显著降低其轨道寿命[10]。

1.2 适用范围

泡沫增阻法适用于低地球轨道(LEO)，这是因为该方法是依靠大气阻力来清除空间碎片，而中、高轨的大气过于稀薄，即使是大面质比的泡沫也难以在短时间内再入大气层烧毁。而且，已经有多项研究表明，高度低于1 000 km的大倾角轨道上的空间碎片是威胁较大、急需清除的目标[11-12]。

泡沫增阻法适用于大尺寸空间目标，主要包括火箭残骸和失效航天器，而不适用于清除尺寸较小的目标，一是因为较小的目标会增加远距离瞄准和精确喷射的难度，二是因为小碎片的数量极多，而卫星的机动能力有限，一颗卫星只能清除少量碎片，效果不明显。而大尺寸空间碎片是空间碎片产生的根源，它们之间的相互碰撞会产生大量的小碎片，引发Kessler效应[13]，这是空间碎片环境不断恶化的主要原因。如果要从根本上限制空间碎片的增长，则应以大尺寸空间碎片为主要清除目标。研究表明，如果每年清除5个大空间碎片，空间碎片总数就可以基本保持不变，维持在一个相对稳定的状态[14-15]。

1.3 优点与不足

泡沫增阻法的优点：

(1) 不需要捕获装置，因此结构简单易实现，并且避免了近距离操作时碰撞的危险；

(2) 空间碎片在再入的过程中不需要控制，可以实现无控再入；

(3) 空间碎片在再入的过程中，只利用大气阻力，不需要耗费激光、离子束等额外的能源；

(4) 潜在危险较小，即使泡沫没有喷射到或粘附到目标空间碎片上，因为其超大面质比，也会在很短时间内再入大气层，如直径30 cm的泡沫能在4个月内从900 km的轨道高度上坠落，不会形成新的长期在轨的空间碎片[9]。

泡沫增阻法的实现也有一些难点和关键技术需要攻克，主要是泡沫的膨胀能力，以及在高速交会情况下对空间碎片的粘附能力，这需要材料科学领域的进步。在轨道领域，需要实现高精度的轨道测定和轨道机动以减少喷射误差，这是本文要研究的问题。

2 泡沫喷射运动分析

考虑一般情况，称初始时刻卫星所在的轨道为初始轨道，目标空间碎片所在的轨道为目标轨道，两轨道的高度不同且异面。令卫星变轨，在目标轨道与初始轨道面的交点处接近空间碎片，并向其喷射泡沫，这种情况下，卫星的机动变轨可以在初始轨道面内实现，无需进行异面变轨，从而节省能量。

卫星与空间碎片接近时的轨道如图1所示。

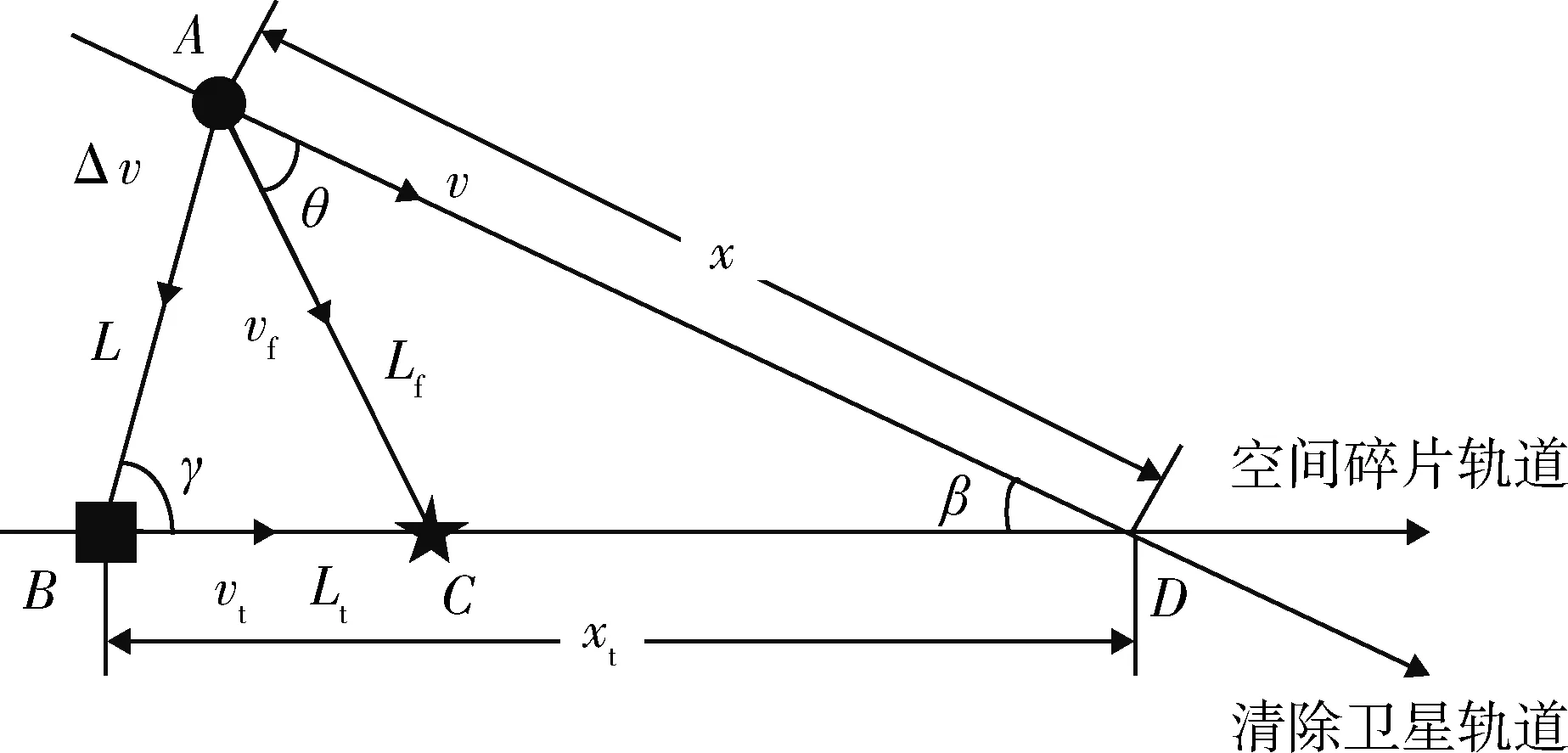
图1 卫星与空间碎片接近示意图Fig.1 Diagram of satellite close to space debris

图1中，A点为喷射泡沫时卫星的位置，也是泡沫的初始位置；B点为喷射泡沫时空间碎片的位置；C点为泡沫与空间碎片交会的点，定义为粘附点；D点为目标轨道与初始轨道面的交点，定义为穿越点；v为卫星运行速度；vt为空间碎片运行速度；Δv为泡沫喷射速度，其方向沿卫星和空间碎片的连线方向；vf为泡沫被喷射出后的运行速度；x为喷射泡沫时卫星与穿越点的距离；xt为空间碎片与穿越点的距离；L为喷射泡沫时卫星与空间碎片的距离；Lt为泡沫与粘附点的距离；Lf为空间碎片与粘附点的距离；β为卫星轨道与空间碎片轨道的夹角；θ为泡沫运行速度与卫星运行速度的夹角；γ为卫星和空间碎片的连线与空间碎片轨道的夹角。

在卫星接近空间碎片时，测距设备测量两者的相对距离，当距离接近到预定值L时，卫星喷射泡沫。为了使泡沫能够被精确地喷射到空间碎片上，即泡沫和空间碎片能够在粘附点交会，在喷射泡沫时卫星和空间碎片需要位于指定的位置，即与穿越点相距x和xt的位置。

设卫星轨道、空间碎片轨道、喷射时卫星与碎片相对距离和泡沫喷射速度已知，即v，vt，β，L和Δv确定，在△ABD中由正弦定理得

(1)

(2)

式中：γ角是未知数。

在△ABC中

(3)

因为泡沫与空间碎片需要同时抵达C点，所以式(3)可变为

(4)

由速度合成三角形得

(5)

由式(5)可得，θ只是未知数γ的函数。将式(5)代入式(4)，都得到一个只含有未知数γ的方程。求解得到γ，并代入式(1)和式(2)得到x和xt。

3 泡沫喷射误差分析

3.1 泡沫喷射误差计算模型

因为对卫星和空间碎片的定轨误差、卫星机动变轨的执行误差，当卫星与空间碎片的相对距离达到预定值L时，卫星和空间碎片不能位于正确的位置，即x和xt出现误差，这会导致出现喷射误差，泡沫不能被喷射到空间碎片上。

设卫星的位置误差为Δx，则卫星的位置x′=x+Δx。根据式可求得γ′角，再根据式可求得θ′角。在△ACD中，泡沫飞行到空间碎片轨道上时经过的距离和时间为

(6)

(7)

该点与空间碎片的距离Lt′由式(3)可得。在时间t′内，空间碎片飞过的距离为

(8)

则喷射误差为

(9)

3.2 最大允许喷射误差分析

为了使泡沫能够接触并粘附在空间碎片上，两者必须有一定的接触深度，如图2所示。因为空间碎片形状不规则，为简化分析，设其截面为正方形。

图2 泡沫与空间碎片的最小接触深度示意图Fig.2 Diagram of minimum contact depth of foam and space debris

图2中，rf为泡沫球半径，rt为空间碎片边长的一半，rmin为两者的接触深度，则所允许的喷射误差最大值为

ΔLt max=rf+rt-rmin.

(10)

空间碎片的质量mt不同，所需的泡沫量不同，最优的泡沫球半径为[9]

(11)

式中：ρf为泡沫的密度。

空间碎片的尺寸rt为

(12)

式中：α为空间碎片的面质比。

4 仿真结果与分析

4.1 泡沫喷射误差影响因素分析

有诸多因素会影响泡沫喷射误差，本文通过仿真，分析卫星与空间碎片的轨道夹角β、喷射时卫星与碎片相对距离的预定值L、喷射速度Δv和卫星的位置误差为Δx对喷射误差ΔLt的影响。

4种影响因素的仿真区间分别为β∈[5°,175°]，L∈[5 km,15 km]，Δv∈[10 m/s,100 m/s]，Δx∈[50 m,200 m]。对各因素独立进行分析，即在分析一种因素的影响时，其他3种因素取固定值，在本研究中，固定取值分别为β=20°，L=10 km，Δv=50 m/s，Δx=100 m。设卫星初始轨道高度600 km，目标空间碎片轨道高度900 km。仿真结果如图3所示。

图3 喷射误差影响因素仿真结果Fig.3 Simulation results of influence factors of ejection error

从图3a)中可以看出，随着卫星与空间碎片的轨道夹角β的增大，喷射误差迅速增大，然后增速逐渐变缓，当β大于50°时，喷射误差基本保持不变；从图3b)中可以看出，随着喷射泡沫时卫星与空间碎片的相对距离L的增大，喷射误差逐渐减小，且减小的速度逐渐降低；从图3c)中可以看出，随着泡沫喷射速度Δv的增大，喷射误差逐渐减小，且两者基本上成线性关系；从图3d)中可以看出，随着卫星位置误差Δx的增大，喷射误差逐渐增大，且两者基本上成线性关系。

除了喷射误差随各影响因素的变化趋势，从图3中还可以看出喷射误差对各影响因素的灵敏度。轨道夹角β和位置误差Δx对喷射误差的影响较大，在仿真区间内，喷射误差的变化均超过百米，其中，喷射误差随位置误差Δx的变化达到300 m；而相对距离L和喷射速度Δv对喷射误差的影响较小，在仿真区间内，喷射误差的变化仅10 m左右。

通过上述分析，可以为提高喷射精度采取针对性的措施，使轨道夹角β和位置误差Δx尽量减小，而相对距离L和喷射速度Δv尽量增大，而且对前两者的改善更为重要。在实施碎片清除任务时，为节省能量，在机动时一般不改变轨道夹角β，而且在任务设计阶段可以通过轨道规划来实现较小的轨道夹角，因此减小位置误差Δx是减小喷射误差、提高喷射精度的最为有效的手段。

4.2 空间碎片质量对喷射误差的约束

由理论分析可知，对喷射精度的需求取决于空间碎片的质量。因此通过仿真分析不同碎片质量所允许的最大喷射误差，同时对卫星的位置误差Δx提出要求。

仿真中，各参数的取值为：泡沫密度ρf=1 kg/m3，空间碎片面质比α=0.02 m2/kg，最小接触深度rmin=10 cm[9]，相对距离L=20 km，喷射速度Δv=100 m/s，β=5°。仿真结果如表1所示。

表1 不同空间碎片质量对喷射误差的需求Table 1 Allowable errors for space debris of different mass

从表1中可以看出，随着空间碎片质量的增大，为使泡沫能够粘附在空间碎片上所允许的最大喷射误差ΔLt max也逐渐增大，进而喷射泡沫时所允许的卫星的最大位置误差Δxmax也增大。对于较小的空间碎片，泡沫增阻法对测定轨精度、轨道机动精度的要求过高，适用性较差。当空间碎片质量mt=500 kg时，其截面边长为3.2 m，这说明泡沫增阻法适用于米级的空间碎片。

4 结束语

泡沫增阻法是一种清除空间碎片的新方法，本文研究了该方法的运动学原理，分析了影响泡沫喷射误差的因素，即卫星与空间碎片的轨道夹角、喷射时卫星与碎片相对距离的预定值、泡沫喷射速度和卫星的位置误差，通过仿真证明，在4种影响因素中提高卫星的位置精度是减小喷射误差的最有效的手段。在此基础上，研究了清除不同大小的空间碎片所允许的最大喷射误差，分析了泡沫增阻法适用的空间碎片的尺寸，并对卫星的轨道精度提出了要求。本文的研究为泡沫增阻法的实现提供了一定的理论基础和参考，为进一步提高该方法的可行性，需要在泡沫的膨胀能力、高速交会情况下对空间碎片的粘附能力等方面进行深入的研究。