改进粒子群算法的防空导弹目标分配方法研究*
阎炼,宋海凌
(海军研究院,北京 100161)
0 引言
在水面舰艇防空问题中,飞机、各类反舰导弹、制导炸弹等空中兵器对水面舰艇的生存构成严重威胁。如何提高舰载防空系统防御能力是水面舰艇防空体系面临的巨大挑战。
水面舰艇对空防御通常使用硬武器与软武器相结合的作战方式。硬武器一般包括舰空导弹和近程反导舰炮武器系统。其中,多目标能力强、射程远、速度快的舰空导弹武器系统是拦截反舰导弹的首选武器。从舰艇配备的防空武器种类来看,既有配备一型舰空导弹的舰艇,也有配备不同射程多型舰空导弹的舰艇。
配备一型防空导弹的舰艇例如“基隆”级驱逐舰,配置“标准-2”舰空导弹。目前越来越多的舰艇配置多型舰空导弹,例如“阿利·伯克”级驱逐舰,“伯克”级配置了MK-41通用垂直发射系统,该发射系统可发射“海麻雀”、“标准-2”、“标准-3”以及“标准-6”等舰空导弹。其中,“海麻雀”舰空导弹制导体制为全程连续波半主动雷达寻的制导,“标准-2”舰空导弹制导体制为末段半主动雷达寻的制导,“标准-3”舰空导弹制导体制为末段被动红外成像寻的制导,“标准-6”舰空导弹制导体制为末段主动雷达/半主动雷达寻的制导。
“伯克”级舰艇配备了3个SPG-62照射器,用来给末段半主动雷达寻的制导的舰空导弹导引头提供制导照射,每部SPG-62能在360°范围内旋转,实现对不同方向来袭目标的照射,为多枚舰空导弹提供服务。例如,“伯克”级舰艇虽然只有3个照射器,但其多目标能力可达12~16个。
因此,研究舰艇配置多型舰空导弹下的目标分配算法,优化分配原则,充分利用防空资源,提高舰载防空导弹武器系统的体系拦截能力具有重要意义。
1 舰空导弹防空作战流程
对空搜索雷达开机后对全空域进行搜索,发现目标后自动转入跟踪,将目标数据传给指挥与决策系统,由指挥与决策系统进行威胁判断与目标分配,将目标分配给武器系统。武器控制系统接收来自指挥与决策系统的目标分配指令、威胁评估结果和雷达的跟踪数据,进行火力通道组织,包括决定拦截方式,选择射击通道。再通过发控系统装订参数,控制导弹发射。舰空导弹防空作战流程如图1所示。

图1 舰空导弹防空作战流程Fig.1 Defense operational process of ship-to-air missile
本文主要研究目标分配算法,不仅包括指挥与决策系统中将目标分配给多型舰空导弹,也包括舰空导弹的火力通道组织。
目标分配是防空作战过程中的重要环节,是确定由哪些火力通道对哪些目标在何时采取什么样的射击方案进行射击,以协调各武器系统作战行为的协调指挥过程。其主要目的是充分发挥各个武器系统的整体优势,寻求在给定约束条件下,符合分配原则的最佳方案,并及时有效地分配防御武器,从而构成整体优化的火力打击体系,在有效消除敌方目标威胁的同时,使防御方所遭受的损失减小到最小[1-5]。
对于配备多型舰空导弹,且多型舰空导弹同时使用照射器资源的舰艇,在目标分配时,需要协调照射资源,优化目标分配原则,最大限度的发挥舰空导弹的作战效能。
2 目标分配算法选择
目标分配问题的解空间会随武器总数和目标总数的增加而呈指数级增长,属于NP完全问题[6-7]。国内外对于目标分配问题的研究重点是模型研究和算法研究[8]。
目前,目标分配优化算法可归纳总结为常规解析目标分配法、智能进化目标分配法和混合式目标分配法3种方法。
常规解析目标分配法是将求解问题抽象化、形象化,用数学的方法进行求解得出最优解。早期对目标分配问题的研究多用常规解析目标分配法[9]。由于计算量大,这类算法在处理大规模问题时通常存在求解时间长的缺点[10]。
智能进化算法是以模拟自然界生物进化过程的优化算法,可利用个体的简单、有限行为拓展到群体的、完成复杂任务的整体能力。其中常见的有粒子群算法、遗传算法、蚁群算法[11-12]等。
混合式目标分配法是将解析法与智能算法相结合,或智能算法之间相结合使用,也是现阶段研究和关注较多的方法。
本文使用智能算法中的粒子群优化算法(PSO)解决目标分配问题。PSO算法是一种进化计算技术,最早是由Kennedy与Eberhart于1995年提出的[13]。源于对鸟群捕食的行为研究的PSO算法同遗传算法类似,是一种基于迭代的优化工具。系统初始化一组随机解,通过追随个体极值和群体极值,在连续空间内迭代搜寻最优值[14-15]。该算法具有收敛能力强,易于实现等优点。在使用PSO算法解决目标分配问题中,如何选取合适的粒子编码形式,如何定义算法中的粒子位置与速度,以及如何提高PSO算法的搜索能力是目前重点研究的问题。文献[16]通过将粒子之间相似度的概念引入PSO算法中,提高了粒子的寻优能力。文献[17]利用粒子相似度对PSO算法中的位置与速度重新定义,从而使PSO算法的搜索过程更加适用于目标分配问题。本文在此基础上增加了照射器数量的约束条件,改进了惯性权重ω,同时考虑了武器对目标拦截可行性以及目标威胁程度,使之应用于多型舰空导弹的目标分配问题。
3 基于改进粒子群算法的目标分配
3.1 目标分配模型
本文研究多型舰空导弹目标分配模型。假设水面舰艇配备m型舰空导弹W1,W2,…,Wm,制导方式皆为末段半主动雷达寻的制导。每型舰空导弹Wi拥有ri个火力通道,m型舰空导弹共同使用的照射器数量为u,在舰空导弹与目标小于某固定距离时照射器开始照射目标直至舰空导弹拦截目标。来袭空中目标数量为n,分别为T1,T2,…,Tn。引入目标分配矩阵
(1)
若分配了武器Wi迎击目标Tj,则xij=1,否则xij=0。以分配给舰空导弹迎击全部目标的失败概率之和作为目标函数,求其最小值,则可推导出最优化目标分配模型为
(2)
式中:E为多型舰空导弹对所有目标的打击失败概率;qij为第i型武器Wi对第j个目标Tj实施打击的单发毁伤概率;wj为各目标的威胁度权重。
该目标分配模型需包含的约束条件有:
(1) 一型武器分配的目标数不超过该武器的火力通道数;
(2) 一个目标最多分配给一个武器中的一个火力通道;
(3) 一个火力通道最多分配一个目标。
3.2 粒子的编码与解码
PSO算法中的粒子对应优化问题的解,即目标分配问题中的某分配方案。使用PSO算法解决目标分配问题时,针对不同的问题背景可采用不同的编码方式。
粒子群中的粒子可视为一维向量,代表一种分配方案,粒子每一维对应一个火力通道,即粒子维数D=r1+r2+…+rm。假设来袭空中目标数量为n,则粒子每一维数值范围1~n,代表分配至该火力通道的目标。
该粒子编码方式可自动满足目标分配模型(2)中的约束条件(1)和(3)。对于约束条件(2),应在粒子编码时进行检查,使1~n中的某数值在某粒子中至多出现一次。
举例说明,假设将6批目标分配至3型舰空导弹,3型舰空导弹的火力通道数量分别为2,2,1。某次分配结果为:舰空导弹1的2个火力通道分别拦截目标4,1,舰空导弹2的2个火力通道分别拦截目标3,6,舰空导弹3拦截目标5,目标2暂未分配火力通道。则该粒子为[4,1,3,6,5]。其编码方式如图2所示。

图2 某粒子目标分配方案Fig.2 Target allocation scheme of one particle
可见,粒子与目标分配矩阵X一一对应。粒子的解码过程即为从左至右扫描该粒子,得到相应的目标分配矩阵,从而计算该粒子的适应度。
3.3 适应度函数选取
PSO算法的寻优即寻求最优的适应度。本文中适应度对应目标分配模型中的目标函数,为得到舰空导弹迎击全部目标的失败概率E的最小值,可对目标分配模型(2)取倒数。则适应度
(3)
3.4 基于改进PSO算法的目标分配算法流程
改进PSO算法的原理与基本PSO算法相同。其算法流程如下:
(1) 设定种群中粒子个数、迭代次数,按照上文编码方式随机初始化所有粒子。初始化个体最优位置pib以及种群最优位置gb。个体最优位置pib为个体在历次迭代中取到适应度最优值时的位置,种群最优位置gb为目前种群中取到适应度最优值的粒子的位置。
根据舰空导弹的速度vs,目标的速度va及斜距d,计算各舰空导弹分别拦截各目标时的遭遇点x以及遭遇时间t1:
(4)
(5)
来袭目标中既有高空目标也有低空目标,舰空导弹在拦截高空与低空目标时平均速度不同,在相应计算中需根据目标高度进行区分。假设对于武器i拦截目标j,遭遇点x在武器i的杀伤空域之外,则武器i对目标j的杀伤概率会有所降低。为便于计算,在计算适应度时令qij=0。
此外需计算舰空导弹从发射至进入末制导,照射器开始照射的时间t2,假设反舰导弹与目标相距D时进入末制导,则
(6)
之后进入算法的迭代过程。
(2) 对所有粒子求其适应度f(p),以更新个体最优位置pib以及种群最优位置gb。
(3) 对所有粒子的速度进行更新。改进的PSO算法定义了新的粒子移动方式,同时速度被定义为步长,即每次迭代中粒子通过该移动方式移动的次数。粒子pi的速度更新公式为
vi=ωvi+c1r1d(pib-pi)+c2r2d(gb-pi),
(7)
式中:ω为惯性因子;c1为认知因子;c2为社会因子,r1,r2为随机数。对vi取整得到粒子速度。基本PSO算法中,惯性因子ω取固定值1。而在粒子迭代寻优过程中,前期粒子搜索范围较大,粒子的移动步数可适当增大,以提高搜索速度。迭代后期接近最优值,粒子的移动步数应逐渐减小。因此本文中将惯性因子设为变量。惯性因子
ω=ωs-(ωs-ωe)(g/gmax)2,
(8)
式中:ωs为惯性因子初始值;ωe为惯性因子最小值;g为当前迭代次数;gmax为最大迭代次数。惯性因子将随迭代次数增加逐渐减小。公式(7)中其余参数含义及取值与基本PSO算法相同。
两粒子之间距离
d(pi-pj)=k[a|f(pi)-f(pj)|/C+
b(D-S(pi,pj))/D],
(9)
式中:k,a,b为正整数;a+b=1;C为种群中适应度最大值;D为粒子维数。S(pi,pj)为两粒子之间相似度。相似度的确定方法为:将两粒子的第1维至第D维分别进行比较,初始相似度为0,若某一维上两粒子数值不同则相似度加1。

对于照射器数量为u的舰艇,若某分配方案使用的照射器数量超过u,则该方案无效。因此对粒子位置进行更新后,需检查每个粒子是否有效,检查方法如下:根据步骤(1)中各舰空导弹分别拦截各目标时到达遭遇点时间t1与进入末制导时间t2,可计算照射器需要对目标照射的时间:
Δt=t1-t2.
(10)
假设某粒子对应的分配方案中,其中2个火力通道对各自目标的拦截时间分别为ti1,tj1,进入末制导时的飞行时间分别为ti2,tj2。若ti1 (5) 转到步骤(2)进行迭代计算直至求得最优解。 该算法中包含的约束条件有: (1) 一型武器分配的目标数不超过该武器的火力通道数; (2) 一个目标最多分配给一个武器中的一个火力通道; (3) 一个火力通道最多分配一个目标; (4) 每个火力通道分配的目标须在其杀伤空域之内; (5) 某方案中所有火力通道同时使用的照射器数量不超过舰上的照射器数量。 其中约束条件(1)~(3)通过目标分配模型以及算法的编码实现。本文提出的约束条件(4)和(5)是通过对每个粒子对应分配方案中的弹目遭遇时间、照射器照射时间等进行计算实现,即检查粒子在条件(4)和(5)下的有效性。 假设某舰艇配备三型舰空导弹。导弹射程以“海麻雀”、“标准-2”以及“标准-6”舰空导弹为例,分别为50,150以及370 km。火力通道数量分别为2,3,3。三型舰空导弹拦截低空目标时平均速度800 m/s,拦截高空目标时平均速度1 000 m/s。三型舰空导弹均采用惯性中程制导加末段半主动雷达自动寻的制导的复合制导体制。 假设舰艇配备3个照射器,3型舰空导弹共同使用照射器,并假设弹目相对距离15 km时,导弹进入末制导,此时,需要照射器对来袭目标进行照射。 假设在防空作战中,某时刻来袭目标数量为10,各目标运动参数如表1所示。 表1 目标运动参数值Table1 Motion parameter value of target 目标威胁程度可以使用层次分析法进行计算。首先根据经验构造判断矩阵: (11) 可求得该矩阵特征向量,即权向量W=(0.524,0.275,0.1,0.1)T,最大特征根4.265。 威胁隶属函数可将目标的参数数值转化为威胁程度。其中,目标速度v的威胁隶属函数为 uT(v)=1-e-αv, (12) 式中:α=0.005。 目标航路捷径p的隶属函数为 uT(p)=e-βp2, (13) 式中:p≤3;β=0.5。 距离r的威胁隶属函数为 (14) 式中:r1=3.5 km;r2=100 km;r3=300 km。 目标高度h的威胁隶属函数为 (15) 式中:k=10-5;γ=10 m。 由式(15)可根据目标参数值求得威胁值矩阵: (16) 式中:t为目标数量;n为目标参数数量;本文t=10,n=4,btn代表第t个目标第n个因素的威胁值,即第1~4列分别为uT(v),uT(p),uT(r),uT(h)。 对威胁值矩阵B进行归一化得到矩阵B′。与向量W的乘积即为各目标威胁程度的权重向量: F=B′·W=(F1,F2,…,Ft)= (17) 式中:F1,F2,…,Ft表示t个目标的威胁程度权重。即得到10个目标的威胁程度如表2所示。假设3种舰空导弹对各目标的杀伤概率如表3所示。 表2 各目标威胁程度值Table 2 Threat value of target 本次仿真中算法参数选取如下:惯性因子初始值ωs为1,惯性因子最小值ωe为0.4,认知因子c1为2.8,社会因子c2为1.2,式中系数k为1.2,a=b=0.5,最大迭代次数gmax为50,种群粒子数量为100。 将算法应用至该实例中。本次程序用时0.739 s,得到种群最佳适应度值随迭代次数的变化如图3所示。 表3 各舰空导弹对目标杀伤概率Table 3 Killing probability to target of ship-to-air missile 图3 种群最佳适应度变化过程Fig.3 Change process of population optimal fitness 程序迭代16次时得到最佳适应度的粒子[8,3,5,9,1,2,10,4],本次仿真中该粒子适应度为2.754,其对应目标分配方案如表4所示。 表4 目标分配方案Table 4 Target allocation scheme 该分配方案满足照射器数量,舰空导弹射程等约束条件。通过式(2)对最后得到的分配方案进行评价,在本次仿真通过50次迭代搜索到的所有方案中,使用该方案拦截目标时,舰空导弹武器系统体系的拦截能力最强。 本次仿真选取的粒子种群数量较大,从而使粒子群寻优范围更易广,更易求得最佳适应度,同时减少了求得最佳适应度的迭代次数,但会使程序运行时间增加。若实验中对适应度要求较低,可减小粒子群数量以及最大迭代次数以提高算法效率。 本文使用改进粒子群算法,针对多型舰空导弹的目标分配问题进行了研究。该算法中,粒子根据粒子之间相似度进行移动,更加适用于目标分配问题中的粒子编码方式。为解决照射器资源的数量限制问题,在算法中对每一种方案进行拦截时间等计算,增加了粒子的约束条件,对粒子进行筛选。 作为目标威胁排序的结果,粒子适应度计算中增加了各目标威胁程度权重。对实例的仿真表明,该方法可有效解决多型舰空导弹的目标分配问题。3.5 算法中的约束条件
4 仿真校验
4.1 背景条件

(0.100,0.078,0.078,0.106,0.021,
0.056,0117,0.093,0.109,0.111),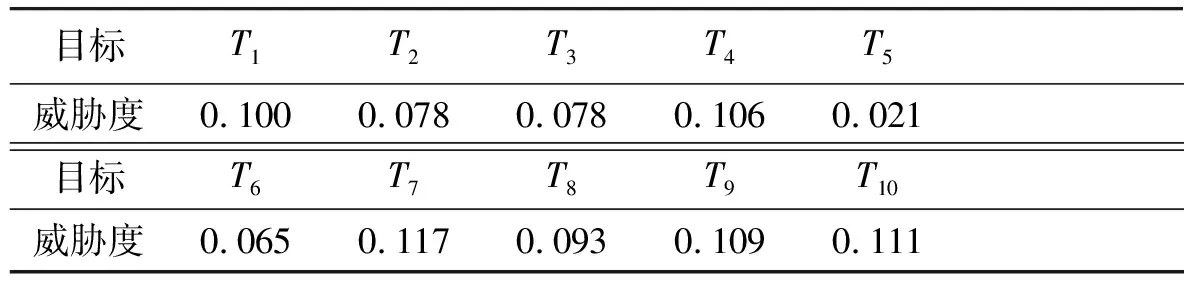
4.2 仿真参数设定
4.3 仿真结果及分析



5 结束语

