考虑导弹速度时变的带落角约束制导律*

龙婧，孔哲，潘涛

(西安航天动力技术研究所，陕西 西安 710025)

0 引言

随着现代战争作战需求的多样化，以及固体变推力发动机技术的发展，小型战术导弹将具有一定程度的自主变速能力，因此在进行末制导律设计时应同时考虑速度变化。但目前大多数基于比例导引律[1-4]、最优制导律[5-8]以及滑模变结构制导律[9-12]而展开的落角约束末制导律研究均假定导弹速度恒定，关于速度时变的研究较少。现有的几篇文献中，马国欣[13]等将导弹的速度信息视为是部分先验已知的，通过对导弹速度曲线进行预测并根据当前时刻测得的实际速度大小对其进行更新，从而得到了导弹速度的变化规律。Taub[14]对预测的速度不断进行数值迭代获得了接近实际的速度变化规律，并基于最优控制极小值原理推导出了落角约束末制导律。这2篇文献都将速度预测为时间的函数，实际过程中需要不断进行更新或者迭代，增加了推导过程的难度。

本文直接将导弹速度假设为相对距离的指数函数，通过建模引入了脱靶量和落角约束，根据最优控制原理直接求解黎卡提方程，获得了考虑速度时变的带落角约束的制导律解析表达式。仿真表明，该制导律能够满足设计要求，并可以适用于不同速度变化的情形，相比传统的最优弹道成型末制导律具有更平直的弹道和更小的需用过载。

1 问题描述与建模

首先进行以下假设：①导弹和目标均视作质点，在二维平面内运动，且目标静止；②忽略导弹和目标受到的重力作用；③末制导阶段导弹速度矢量与弹目连线之间的夹角为小量。末制导段弹目相对运动如图1所示。

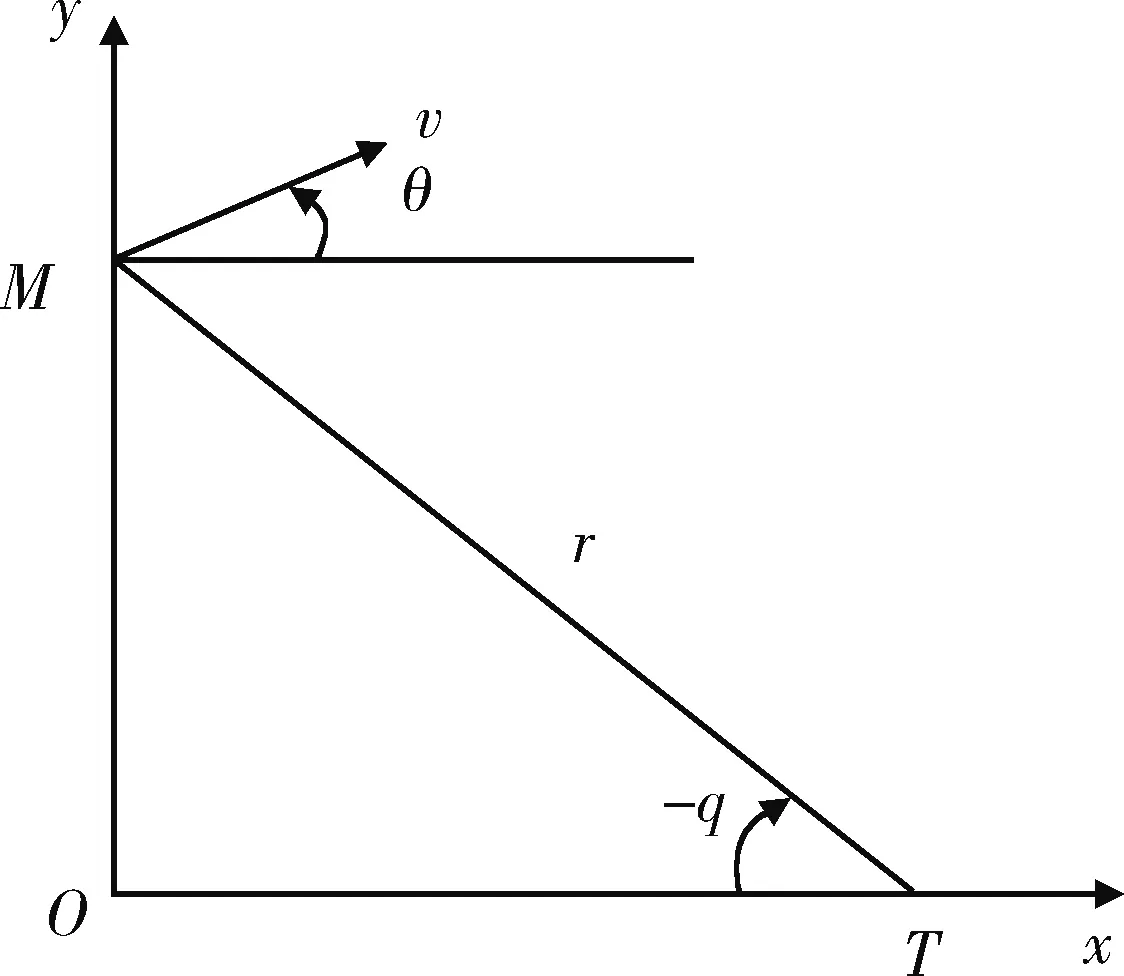
图1 弹目相对运动关系图Fig.1 Relative motion relationship betweenmissile and target

图1中，M代表导弹位置，T代表目标位置。r，q，θ分别为弹目相对距离、目标视线角以及导弹的弹道倾角，v为导弹当前时刻的速度。

相对运动方程可以描述为

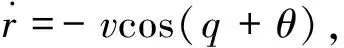
(1)

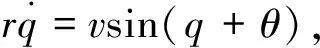
(2)

对式(2)求导并联立式(1)可得

(3)

为了满足脱靶量以及末端落角约束，选取状态变量如下：

(4)

式中：θd为导弹的期望落角。

则上述问题可以表达为系统状态方程的形式：

(5)

终端约束条件为x1(tf)=0，x2(tf)=0。

选择二次型性能指标如下：

(6)

式中：R为对称正定矩阵;F为半正定对称矩阵。选取R=1，F-1=0，将导弹末端约束问题转化为典型的最优控制问题。

2 最优制导律设计

根据最优控制理论[15]可知，第2节描述的问题的最优解存在且唯一，即

u*=-R-1BTPx,

(7)

式中:P为满足黎卡提方程的对称矩阵，可以通过求解逆黎卡提方程得到。

逆黎卡提方程如下：

(8)

令

(9)

由于P为对称矩阵，q12=q21。

则式(8)可以写为

(10)

即

(11)

将式(11)展开后可得

(12)

假定导弹在制导过程中的速度可控，并可近似写成弹目相对距离r的指数函数的形式，如式(13)所示：

v=kra,

(13)

式中：k和a为常数，且满足k>0，a<0。当导弹速度为常值时，a=0。对式(13)求导可得速度变化率为

(14)

此外，根据第1节假设(3)可得

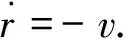
(15)

联立式(12)～(15)求解即可得到矩阵Q如下：

(16)

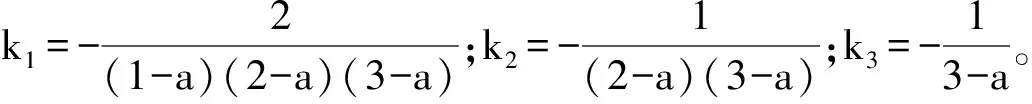
P=Q-1=

(17)

将k1，k2，k3代入式(17)中，则

(18)

将式(7)展开，代入矩阵B，P，x，最终可以得到

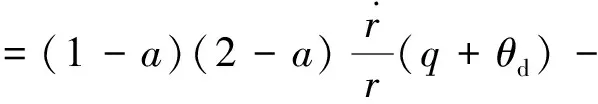
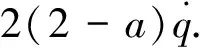
(19)

最优制导律为

(20)

当a=0时，导弹速度为常值，导引律为

(21)

与文献[5]中给出的相同。

1.1 对象 选择2011年1—12月在我院行前列腺电切术患者40例为观察组，年龄53～79岁，平均年龄68.0岁，实施临床护理路径方法;以2010年1—12月在我院行前列腺电切术患者40例为对照组，年龄在56～81岁，平均年龄71.0岁，采用常规护理方法。入选条件:诊断明确，没有严重的合并症，且患者能配合完成各项治疗和护理。两组患者在年龄、文化程度等比较差异无统计学意义(P＞0.05)，具有可比性。

3 仿真分析

设初始时刻导弹的坐标为(0,4 000m)，目标的坐标为(3 000 m,0)。初始时刻导弹的弹道倾角为0，导弹的期望落角为-60°。

(22)

3.1 仿真校验

为了研究不同速度变化情况下本文提出制导律的性能，在上述仿真条件下，分别取a=-0.2，k=550；a=-0.6，k=16 500；以及a=-1，k=500 000进行仿真，结果如图2所示。

仿真结果表明，在初速相同，导弹采用不同的加速度飞向目标的条件下，本文给出的制导律都能够以要求的落角击中目标，导弹轨迹以及弹道倾角变化较为平缓，法向过载较小，而且在弹道末端导弹的法向过载有趋于0的趋势。因此，本文提出的制导律有效且具有良好的综合性能。

3.2 与传统最优制导律对比

为了研究本文给出的末制导律与传统的最优末制导律即式(20)与式(21)的区别，进行了如下仿真。

其次对速度曲线的不同拟合情况进行对比。由图3d)可以看出，拟合速度1的精度高于拟合速度2，所以制导律1相比制导律3具有更平缓的弹道和更小的法向过载，但二者差距并不明显，这说明速度曲线拟合精度要求不必太高。

综上，在较大的拟合精度范围内，本文给出的制导律都具有高于传统最优制导律的综合性能，因此，当导弹速度时变时，可以用速度关于相对距离的指数函数对导弹预设的速度曲线进行拟合，并根据式(20)得到性能良好的制导律。

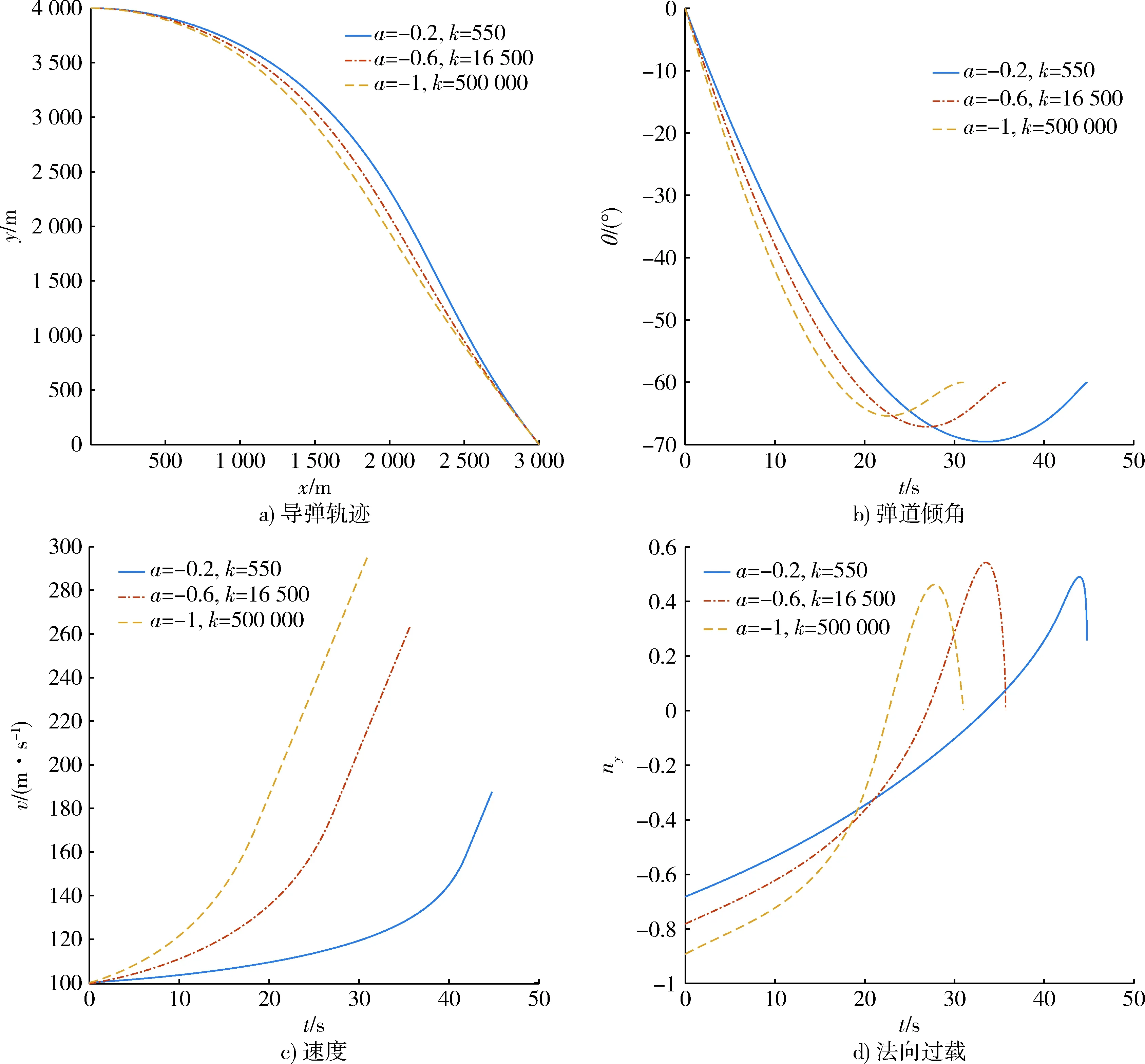
图2 不同参数条件下的仿真结果Fig.2 Simulation results with different parameters

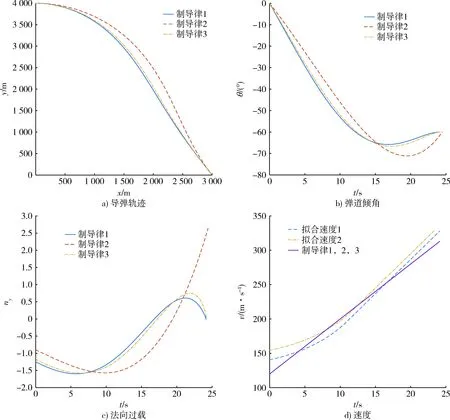
图3 匀加速情况下最优制导律对比Fig.3 Comparison of optimal guidance law with constant acceleration

4 结束语

本文根据小型战术导弹可能具有的自主变速能力，提出了速度时变条件下满足脱靶量和落角约束的最优制导律。仿真结果证明了推导中各个假设的合理性以及该制导律的有效性。所设计的制导律结构简单，精度良好，适用范围广，具有一定的工程应用价值。