用思路点拨法培养学生解综合题能力

张煜彬

一、了解考点与命题趋向，明确解综合题的要求

（一）知识考点及能力培养要求

1.准确地掌握基础知识，具有熟练的基本技能;2.弄清概念，熟记全部定理、法则、公式，特别是定理、法则、公式的适用条件;3.加强分析问题、解决问题的思维训练，逐步提高解题能力;4.通过变式训练，拓展学生思维，提高学生的辨别能力，有利于学生克服思维定势;5.在解题中培养学生的创新意识，巧解复杂、综合的数学问题;6.善于把实际问题转化为数学问题，培养学生用数学知识解决实际问题的能力，这也是素质教育的要求。

（二）解综合题的思想方法和解题过程要求

1.认真审题，善于分解，使综合问题向典型问题转化;2.善于拾漏补遗，力求答案准确无误; 3、善于运用数学思想、方法解综合题;数学方法有待定系数法、分类讨论法、反证法等;数学思想有数形结合、分析与综合、转化、方程等，在解题中能自如地运用。

二、解题方法与技巧的探索，思路方法的培养

学生能力的提高，要依靠在平时的知识积累，在教学中适时拓展知识范围，引导学生自觉地去思考，从特殊想到一般，从抽象想到具体，由此及彼，由里到外，从而培养学生分析和解决问题的能力，逐步提高学生归纳、整理知识的能力。使学生走上发展创新之路，真正实现提高学生解答综合题的能力与技巧的愿望。

下面是我在教学中，根据教学内容适时补充如下类型题目作学生课后思考题，具体实施办法：①先用小黑板公布思考题，并作简要分析，点明解题思路。②多位学生作解后，作评讲，肯定最优方法。③解题方法规律总结。通过长期的训练，学生解综合题能力提高较快，取得了较好的教学效果。 类型题目举例如下。

方法1：数形结合法。（借助图形联想，巧解题）

【例1】如图所示，Rt△AOB的顶点A是直线y=x+m与双曲线y=mx在第一象限内的交点直线y=x+m和x轴交于点C，且S△AOB=3

求：（1）m的值

（2）△ACB的面积

【分析】要求m的值，只需求xy的值即可，由S△AOB=12OB·AB=3，即xy=6，从而求出m的值，确定了直线和双曲线的解析式，最后解方程组，求出两图象的交点A的坐标和BC的长，S△ACB就可以求出。

【解】（略）

【规律总结】此题是函数类形综合题，凡是求函数图象交点问题，常转化为方程组求解，解函数问题常借助图象，这就是数形结合思想的表现形式。

方法2：分类讨论法。（此类题课本中少出现的探索型问题）

【例2】已知二次函数y=ax2+bx+c的图象过点A（2，4），顶点的横坐标为12，它的图象与x轴交于两点B（x1，0），C（x2，0），与y轴交于点D，且x12+x22=13，试问：y轴上是否存在点p，使得△POB与△DOC相似（O为坐标原点）？若存在，试求出过P，B两点直线的解析式，若不存在，请说明理由。

【分析】易求抛物线的解析式为y=-x2+x+6，与x轴交点坐标为（-2，0），（3，0），与y轴的交点坐标为D（0，6），因为题中未给出B，C的确定位置，所以要分两种情况讨论。

【解】（略）

【规律总结】此题是就点的不确定性进行讨论，即点B的坐标有（3，0）或（-2，0）兩种情况。分类讨论思想方法是解探索型问题的一个重要的思想方法。分类的关键是捕捉问题中的不确定因亲，把握了这一点，一些复杂问题也就转化为我们所熟悉的简单问题。

方法3：变换视角。（是逆向思维的运用，巧妙解决问题）

【例3】已知关于x的方程x3-ax2-2ax+a2-1=0有且只有一个实根，求实数a的范围。

【分析】按常规思路，把x当成主元，求出x，再对a进行讨论，解题过程相当繁琐，若把a当作主元，这种反“客”为“主”的转换思维技巧很新颖别致。

【解】原方程可变为：a2-（x2+2x）a+x3-1=0，即[a-（x-1）][a-（x2+x+1）]=0，∴x=a+1或x2+x+1-a=0

因为原方程有且只有一个实根，所以方程x2+x+1-a=0无实根。由△<0  ∴1-4（1-a）<0即a<34。

【规律总结】此题顺向思维不易解决，变换主元，使问题得以巧解达到创新的解法，令人耳目一新。

方法4：转化法。（几何问题可转化为代数问题，也可将三角函数值转化为线段比去解答）

【例4】如图，在正方形ABCD中，F是CD上一点，AE⊥AF，AE交CB的延长线于E，连结EF交AB于G。

（1）求证：DF·FC=BG·CE;

（2）已知当tan∠DAF=13时，△AEF的面积为10m2问当tan∠DAF=23时，△AEF的面积是多少？

【分析】（1）由题设易证Rt△ADF≌Rt△ABEAF=AE，DF=BE，可证Rt△EBG∽Rt△ECF，从而DF·FC=BG·CE。（2）由tan∠DAF=13，可设DF=x，AD=3x，则AE、AF都可由x表示，再根据ΔAEF的面积即可求得x的值，即得AD的值。

【证明】（略）

【规律总结】解此类问题时，若已知条件中合有角的三角函数值，可将其转化为线段的比，这样可使问题得到简解。

方法5：等量转换。（通过几何，代数式的等量代换，使条件和结论能联系一起，使问题易解决）

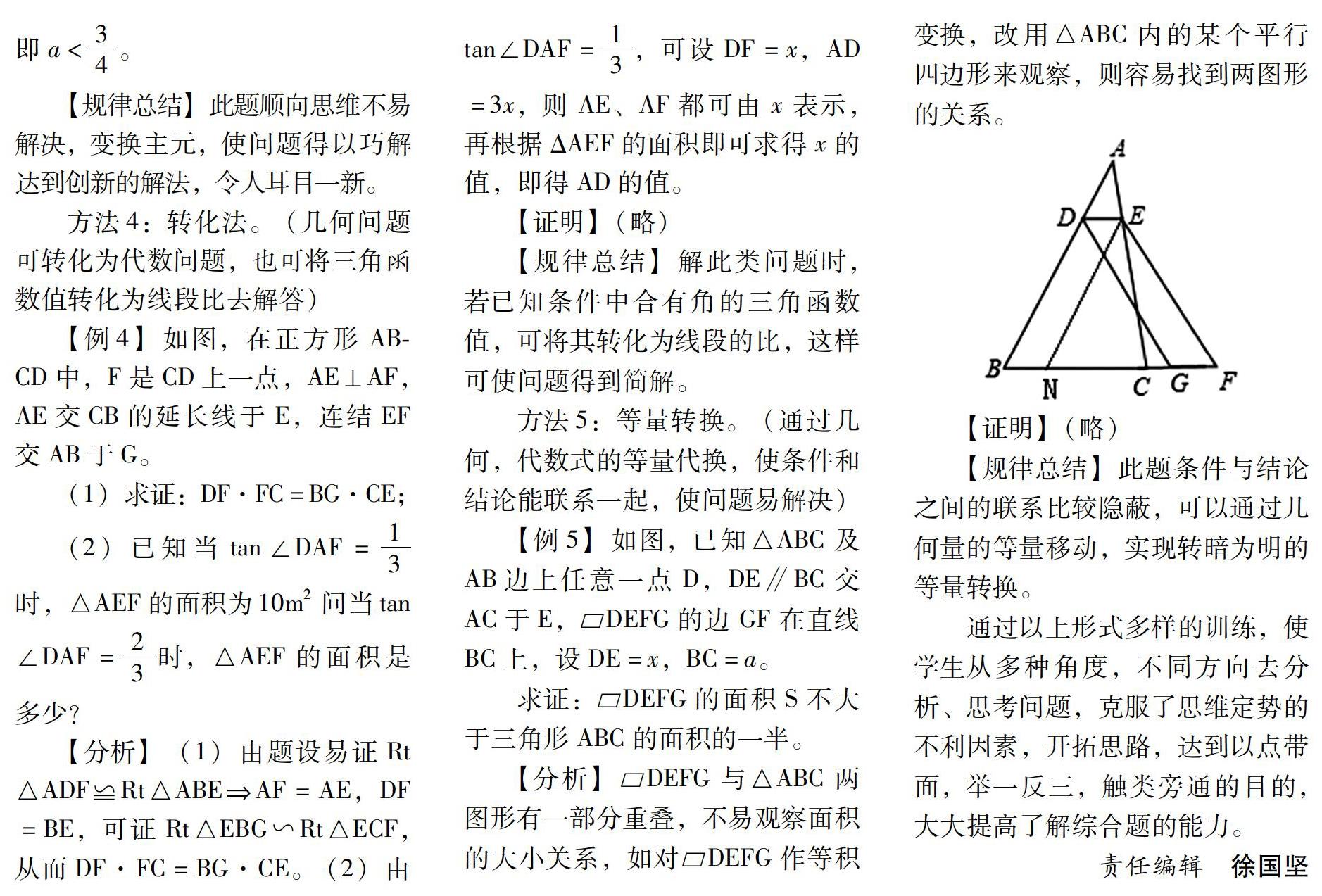
【例5】如图，已知△ABC及AB边上任意一点D，DE∥BC交AC于E，DEFG的边GF在直线BC上，设DE=x，BC=a。

求证：DEFG的面积S不大于三角形ABC的面积的一半。

【分析】DEFG与△ABC两图形有一部分重叠，不易观察面积的大小关系，如对DEFG作等积变换，改用△ABC内的某个平行四边形来观察，则容易找到两图形的关系。

【证明】（略）

【规律总结】此题条件与结论之间的联系比较隐蔽，可以通过几何量的等量移动，实现转暗为明的等量转换。

通过以上形式多样的训练，使学生从多种角度，不同方向去分析、思考问题，克服了思维定势的不利因素，开拓思路，达到以点带面，举一反三，触类旁通的目的，大大提高了解综合题的能力。

责任编辑 徐国坚