插装式溢流阀流体自激振荡仿真研究

，，

(同济大学 机械与能源工程学院,上海 201804)

引言

在挖掘机等工程机械的液压回路里，插装式溢流阀是一种很常见的液压元件，通常被用作安全阀，来承载系统压力。插装式溢流阀在应用广泛的同时，也出现了许多工程问题，比较显著的有两点：① 阀芯在压力作用下打开时，由于流动出口较小，会产生很强的节流效应，从而诱发空化噪声和气蚀等问题； ② 溢流阀的核心部件是阀芯-弹簧，这种结构在受到系统压力波动的影响时，很容易产生振动，诱发振动噪声或者导致溢流阀意外开启。学术界针对这两个问题已经进行了很多研究和改良。

另外，随着挖掘机等工程机械的吨位提升，其液压回路的压力可以达到数十兆帕，对应的流量可以达到每分上百乃至数百升。在这种工况下，插装式溢流阀阀口的流速可以达到数每秒十乃至上百米，马赫数接近0.1甚至更高。在这种工况下，高速液流经过阀口凹腔时会造成剪切层的高频波动，并撞击到后壁产生向上游运动的声波。剪切层波动与反向声波耦合后还会产生更强烈的自持振荡，学术界称为流体自激振荡现象[1]。

对于这种现象提出的最经典的理论是1964年，ROSSITER[2]在研究风洞实验时提出了凹腔自激振荡半经验频率公式和理论，如图1所示。

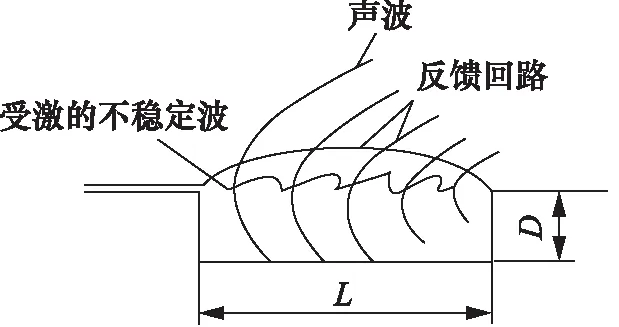
图1 Rossiter的波涡耦合理论模型

Rossiter认为涡流在这一过程中扮演着重要角色，并将其机理解释为：高速流场经过剪切层分离处时与凹腔内流体产生剪切，形成向下游运动的涡流。涡流撞击到凹腔后壁，形成向上游传播的反馈声波，声波到达前壁再次激发涡流，并对涡流的产生形成调制。如此循环往复，形成凹腔内的自激振荡。

Rossiter针对自己的理论模型提出如下经验公式：

n=1,2,3,…

(1)

(2)

(3)

其中，设向下游传播的涡流波长为λ1，向上游传播的声波波长为λC。f为声波频率，v和C分别为自由流流速和声速；S为斯特劳尔哈数；M为马赫数；kv为涡流流速与自由流流速的比值。L为腔长；α为相位滞后；n为模态数，即自激振荡的阶数。

Rossiter的理论模型奠定了流体自激振荡研究的基础，后续的研究大多在修正、补全Rossiter模型的基础上展开。

针对液压阀结构的流体自激振荡研究开始较晚，1986年，BALDWIN和SIMMONS[3]指出在具有分支的管道结构中，气动溢流阀阀口会有涡脱落，并产生声学共振。1997年液压阀公司SUN[4]针对自己设计的Counterbalance Valve进行了仿真实验，并指出阀内产生的啸叫是具有主频的共振噪声。

SUN的仿真实验针对的是气动溢流阀，而现在工程机械中广泛应用的插装式溢流阀通常在液压环境中工作。液压系统相比于气动系统，马赫数要低一些，但是流动介质密度更大，其带来的质量惯性效应也更大。插装式溢流阀在液压系统中所产生的自激振荡会带来怎样的影响，值得进一步研究。

1 插装阀典型结构

1.1 插装阀的典型凹腔流动结构

插装阀通常被安装在集成阀块上，其基本结构如图2所示。

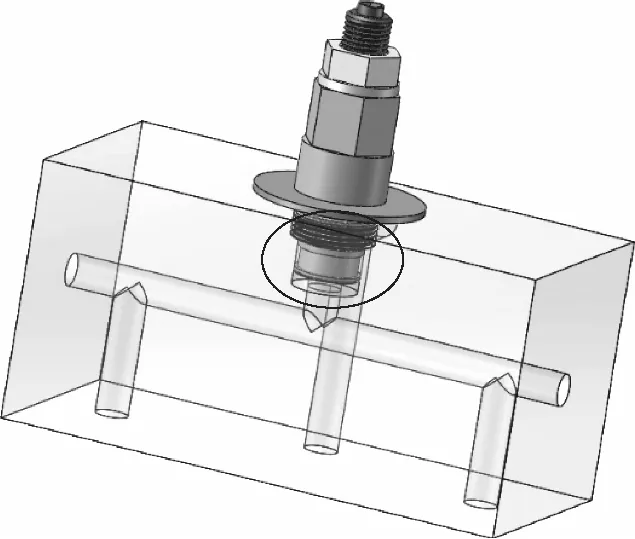
图2 插装阀的基本安装结构示意图

图2中圆圈所标识的位置是插装阀阀块中常见的结构，阀体安装孔道与横向流道构成了“主流流道-凹腔”的特殊结构，这个结构与凹腔自激振荡经典理论中的“自由流-凹腔”结构十分相似，很容易诱发自激振荡现象。

1.2 研究用插装阀参数

为了使仿真具有工程意义，特别选取了真实的插装阀作为仿真结构设计参考。某型号的插装先导式溢流阀为选取结果，其结构如图3所示。

图3 仿真参考插装阀结构示意图

该型号的插装阀与仿真相关的主要参数为：最大流量75.8 L/min，油口直径10 mm，这些数据作为仿真物理模型建立以及计算参数设置的参考。

该插装阀是先导式、锥阀型的溢流阀，通常用作安全阀，或者与其他控制阀配合安装作为压力控制阀。这种溢流阀在工程机械、搬运机械以及农业机械上都有广泛应用。

2 数值仿真

2.1 流场物理模型

截取阀口凹腔与横向流道组成的结构作为流场的物理模型，自激振荡现象主要在这一部分结构中产生，如图4所示。

图4 流场物理模型

流道是圆孔结构，不过其两侧对称，取其中间横截面作为近似结构，进行二维仿真，二维网格划分如图5所示。

与传统的流体自激振荡研究不同，插装阀凹腔外部的并不是自由流场，而是管道流动，管壁对流动存在限制。所以凹腔附近的结构，包括凹腔内部和凹腔外部延伸到管壁的这部分都是研究流动现象的重要区域，所以将这一区域统一加密。剪切层近壁面处也是流体自激振荡现象的重要区域，所以一并加密。

图5 流场网格局部图

2.2 仿真方法及设置

CFD仿真中默认液体为不可压缩流体，但是流体自激振荡是波涡耦合的现象，液体的可压缩性必须考虑进去[5-7]。

使用Fluent的可压缩液体模型，设置流体介质的各项参数如表1所示。

表1 仿真实验介质参数

在可压缩模型下，使用RNG模式的k-e计算模型，这种模型的计算方程为：

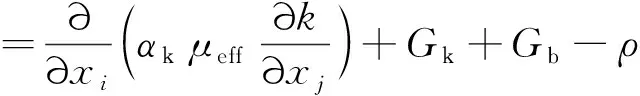
(4)

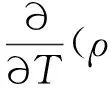
(5)

Gk是由层流速度梯度而产生的湍流动能；Gb是由浮力而产生的湍流动能；YM是在可压缩湍流中，过渡的扩散产生的波动；C,C和R是常量；αk和α是k方程和e方程的湍流Prandtl数，Sk和S是用户定义源项，一般采用Fluent内置的默认值。但是由于k-e模型本质上是个半经验公式，某些情况下为了更好地与真实实验结果契合，可以在UDF文档里修改Sk和Se的数值，以达到更好的模拟效果。

比起标准k-e模型，RNG模式的k-e模型考虑了湍流中的漩涡，在这方面精度更高，并且更适合近壁面的剪切流动，十分切合插装阀凹腔流体自激振荡的仿真需要。

另外，由于流体自激振荡现象是一种波涡耦合的流动现象，需要采用流动-压力耦合的算法[5]，采用Coupled算法进行求解。

根据涡的运动速度及凹腔宽度，设置仿真步长为10-6s，仿真步数为2000步。

由于流体自激振荡在马赫数太低的时候会渐渐消失，成为宽频噪声[8]，所以为了观察到阀口凹腔内的自激振荡现象提高马赫数，设置流速为125 m/s，液体内声速为1300 m/s，对应马赫数为0.1。

3 结果与分析

3.1 凹腔剪切层上的涡流运动

从仿真结果中每5个步长提取一次流动图像，可以发现，经过初始阶段后，会有漩涡从凹腔前壁周期性地脱落。取其稳定阶段的一个周期，如图6所示。

图6 涡运动过程示意图

图6展示了一个涡从凹腔前壁脱落并撞击到凹腔后壁的过程，可以观察到当上一个涡撞击到后壁的时候，下一个涡刚好从前壁脱落。

剪切层稳定后这个过程周期性地发生，初步印证了Rossiter理论中的自激振荡机理描述。

由于还没有对仿真结果进行过声学分析计算，所以参考Rossiter理论中的涡流频率假设，用涡脱落的频率对自激振荡频率进行估算。对整个仿真时间内经历的所有完整涡运动周期取平均值，得到涡出现的周期约为90个步长。

涡流频率即涡脱落的频率，可以得到涡流的仿真频率：

由于当上一个涡撞击到后壁的时候，下一个涡刚好从前壁产生，一个周期内在剪切层上最多会出现2个涡，可以估算出Rossiter理论中的涡流波长λ1在本案例中约为凹腔长度L的一半，则涡流的流速为：

进而得到：

kv≈0.44

而相位滞后α一般取0.25[8]，分析涡的运动过程可以得到这个凹腔的涡运动所对应的自激振荡模态n为2，则可以通过式(3)计算得到自激振荡的声学频率：

Rossiter理论中假设fs=fc，而计算结果是fs略大于fc，可认为两者近似。

出现这种现象的原因可能是纯粹从图片上的漩涡运动来估算涡流周期，导致出现误差；也可能是本案例中的实际相位滞后α要比0.25小，相位滞后α取值0.25，导致计算频率偏大。

另外，根据HELLER等[8]的理论，凹腔内的真实马赫数要根据当地介质的比热容进行调整，凹腔内的真实马赫数要比根据自由流流速和声速计算得到的马赫数小，这也可能是fc偏小的原因，有待进一步的实验验证。

3.2 腔底压力波动现象

仿真时设置监测器对凹腔底部压力进行检测，并将数据导出，可以得到腔底压力波动曲线，如图7所示。

图7 腔底压力波动

可以看出在初始扰动消失后，凹腔底部出现了周期性的压力波动，这种压力波动直接作用在插装阀阀芯上，可以认为是插装阀阀芯振动和意外开启的原因。

如图8所示，通过频谱分析可以得到压力波动是多个高频震荡信号的叠加，这些频率信号是成整倍数的谐振频率，其基础频率约为11718 Hz，正好与通过涡脱落估算的自激振荡主频十分接近，可以推测这种压力波动的频率与凹腔中的自激振荡频率有直接的关系。

图8 腔底压力波动频谱分析

这种关系可以描述为，在流体自激振荡发生的同时，剪切层的波动引起了凹腔内的质量流动，这种质量流动导致了腔底的压力波动。在液压环境中，液压油密度远大于气体，质量的惯性效应也更强，这种质量流动所导致的压力波动对液压系统的影响要远大于气动系统。

凹腔内流体自激振荡频率与凹腔宽度及横向流道流速直接相关，由于腔底压力波动与凹腔内自激振荡频率之间存在直接关系，可以针对不同流速对插装阀凹腔尺寸提出设计建议。首先在特定的流速下可以通过选取合适的凹腔长深比来降低自激振荡频率，从而抑制这种压力波动；或者选取合适的弹簧，使弹簧的共振频率避开压力波动频率，提高插装阀稳定性和使用寿命。

4 结论

(1) 针对插装阀凹腔结构，使用RNG模式的k-e模型和Coupled算法建立了可压缩的、流动-压力耦合的Fluent仿真模型；

(2) 通过仿真获得了剪切层涡流图像，涡流频率与Rossiter半经验频率公式计算得到的自激振荡频率相比偏大，误差可能源于相位滞后α的取值和凹腔内马赫数M的变化；

(3) 通过在凹腔底部设置监测器，同步获得了腔底的压力波动信号，这种压力波动在一定程度上可以认为是源于剪切层波动引起的凹腔内质量流动，其波动频率与估算的自激振荡主频十分接近；

(4) 根据估算的自激振荡主频与腔底压力波动频率之间的关系，可以通过设计合适的凹腔长深比来抑制腔底压力波动，也可以通过选取合适的弹簧来避免压力波动与弹簧产生共振。