分布式系统实时信号级仿真实现方法*

邱 岚，胡 莉

（1.江西科技学院信息工程学院，南昌 330098；2.河北师范大学信息技术学院，石家庄 050024）

0 引言

仿真技术是以相似原理、系统技术、信息技术以及仿真应用领域的有关专业技术为基础，以计算机系统、与应用有关的物理效应设备以及仿真器为工具，利用模型对实际系统进行研究的一门多科学综合性技术[1]。随着现代信息技术的高速发展，仿真技术也得到了长足进步，在军用和民用领域中的应用更是不断向深度和广度拓展。对于仿真系统的要求也越来越高，目前，就军用仿真系统而言，主要分为功能级仿真系统和信号级仿真系统[2]。功能级仿真系统主要是检测该系统能否实现预期功能，对于系统中细节部分关注较少。优点在于仿真速度快；而缺点在于仿真精度低。信号级仿真系统更接近真实系统，主要用于对系统中应用的相关算法、系统结构以及系统功能进行研究。优点在于系统结构反映清晰、仿真精度高；而缺点在于计算量大，运行速度慢。

目前，国内对于解决分布式系统的实时信号处理问题主要集中于硬件提升以及算法上，传统的应用实时处理机制多是利用构建系统模型，牺牲空间来弥补时间上的不足，这样的仿真系统过于繁琐，应用受限。现代军用仿真系统主要应用于战场环境、电子对抗等方面，用来对战术战法、武器系统研制以及各项处理算法进行研究。根据以上特点，系统必须具备运行速度快、逼真度高等条件。所以研究一种实现实时性、信号级仿真系统的方法十分必要。目前，制约信号级仿真的最大障碍就是系统的运行速度，文献[3]中利用并行计算模式构造了相控阵雷达仿真系统，提高了系统运行速度，其实质在于利用大量的计算机资源换取计算速度，但计算量却没有降低。

本文结合透明计算实现结构，提出一种实时信号级仿真系统的实现方法。该方法主要是根据透明计算概念中，软、硬件分离的思想，改变仿真系统中信号发射端和接收端的结构，将信号的特征值代替信号采样数据作为各节点间传输信息，传输的数据量大大减小，从而最终使系统达到实时仿真。

1 原理介绍

文献[4]中是这样描述透明计算的：透明计算模式由服务器以及终端机组成，用户通过网络，向服务器提出要求，服务器根据要求，下发指令至各用户，由各用户所持有的终端产生用户所需要的资源。这种计算模式使得用户能够根据自己的兴趣和需要去选择资源，减少了资源浪费；同时服务器只用于储存，不从事应用计算，提高了用户响应速度。这种模式也可理解为远端提供指令；本地提供硬件，根据用户所需，获取远端技术指令，并在本地生成对应数据。这种方式的好处在于远端无需提供用户所需全部数据，通过指令指导用户本地硬件产生对应数据，大大减少传输数据量，缩短响应时间。

在仿真领域定义3种时间：自然时间、机器时间和仿真时间[5]。自然时间为客观世界的现实时间；仿真时间为仿真系统产生的仿真世界的时间。只有当自然时间等于仿真时间时，才能认为该仿真具有实时性。通常，在实时性要求很高的军事仿真领域，相邻的两次仿真时间间隔不应超过1/60 s，否则仿真人员往往在下达指令后无法立刻得到系统响应，产生延迟的感觉[6-7]。

信号级系统仿真时，大数据量的传输导致了整个系统的计算、响应速度变慢，无法适应现代军用仿真的要求。信号经采样后，每秒传输的数据量为几兆至几十兆不等，而对于一些信号源数目较多的系统，比如雷达组网仿真、雷达侦察仿真等系统，在进行仿真时，在传输线上每秒所需要传递的数据量就会达到几百兆甚至更大，所以降低传递的数据量是改善系统运行速度的关键。

根据透明计算的模式结构，将仿真系统的信号发射端和接收端类比于服务器和终端机，服务器将对终端机用户的需求提供技术指导，最终用户的需求通过技术指导，在本地生成所需资源，这样直接减少了数据传递量，并且也能完成用户所需。同样的，仿真系统也能通过此方法减少数据量，信号发射端提供产生发射信号所需的足够特征值，将特征值数据传递给信号的接收端，接收端利用信号特征值信息，在接收端产生信号，直接进行处理。这样系统传输的不再是大量的信号采样后的数据，取而代之的则是信号特征值数据。很明显，系统各节点间传递的数据量大幅减少。系统结构如图1所示。

图1 发射、接收端结构

图1重新规定了仿真系统中的信号发射、接收端结构。按照透明计算的软硬件分离的思想[9-10]，将产生信号的硬件结构安置于信号的接收端，这样信号发射端产生的只是所要产生信号的特征值，接收端利用特征值在本地信号复原模块上进行信号复原，并得到信号数据，进一步处理。

该原理也可理解为系统任务分割并重新组合的一类决策问题[8]。将系统的每一节点所需完成的任务进行分割，例如信号发射端，产生发射信号的任务可以进行再分割，可分为信号特征值提取和信号复原两部分。若进行这样的分割还是无法达到预期效果，则可以进一步细化。细化后的节点拓扑图按照所需要求进行重组，得到最优系统结构。重组前后拓扑结构如图2所示。

图2 系统拓扑结构

图2（a）中，将系统任务分为3部分，并将任务1，2，3赋予系统各节点。任务1为信号产生；任务2为信号接收；任务3为信号处理。图2（b）中，任务1被重新划分，分为新的任务1，任务4和任务5。任务1为信号产生，任务4为信号特征值提取，任务5为信号复原。将信号复原硬件安装在信号接收硬件部分，也就是说，信号复原和信号接收的硬件部分在同一台PC机上，且信号特征值在系统各节点间的传递可视为实时传递，所以信号产生和传递便不存在时间延迟等问题。

2 实验验证

该实时信号级系统仿真方法已经应用于雷达侦察分布式系统中[11-13]。雷达侦察仿真系统，主要分为3个部分，分别为导演控制台、雷达信号产生子系统和雷达信号接收机子系统。两个子系统分别用不同的PC机实现，数据通过传输线传输。雷达信号产生子系统中，包括火控、警戒等9部雷达仿真模块，采样率为1 M/s，9部雷达仿真模块同时产生仿真信号，则雷达信号产生子系统每秒产生的采样后的数据量为9 M，数据传输的时候就会产生数据冗余，传输速度变慢，导致响应无法实时产生回应，失去了仿真的意义。应用本文提出的方法，解决了此问题，使得分布式雷达侦察仿真系统成为真正意义上的实时信号级仿真系统。各子系统间数据传递的示意图如图3所示。

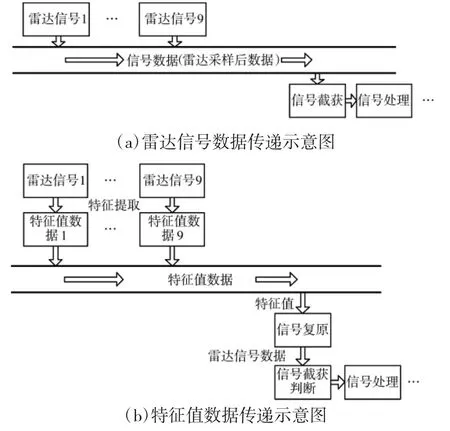
图3 数据传递示意图

当仿真开始后，雷达信号发射系统根据任务想定，从导演控制台处接受指令，产生相应类型信号，并通过局域网向雷达侦察子系统传递信号数据[14]。根据不同的需求，发射系统所产生的数据量的大小就会产生差别[15]。数据量大时，势必会产生传输速度慢、系统不能及时响应等问题。所以根据本文方法，将传递的数据量转换为足够多的特征值进行传递以解决该问题。

2.1 数据传输耗时对比实验

假设，本次实验的源信号为9部雷达同时产生的，信号类型为线性调频、伪码调相以及Barker编码。利用SystemVue软件产生以上几类信号，具体参数见下页表1。

通过改变3种类型信号的脉冲重复周期实现9个雷达信号。信号产生后，SystemVue软件能够形成雷达信号数据，又由于本次实验是在信号级下进行仿真，采样点数达到了1 M，而每个点就是雷达信号时域的幅度值，换算成比特，每个雷达信号每次采样就会产生8 Mb的数据量，9个雷达信号大约就会产生72 Mb以上的数据量，传输时必然会产生时延。将数据打包，最终需要传递的数据量为85 032 kb，利用传输软件，在局域网中将100次实验得到的雷达信号数据进行传输，传输时间如下页图4所示。

实验中，平均传输速率为11.3 Mb/s。通过计算得到100次实验平均耗时为7.373 6 s，远远超过了仿真预期耗时，无法达到实时性系统的要求。按照本文提出的方法改变仿真系统结构，子系统间传输的数据由雷达信号采样数据变为雷达信号特征值数据，包括信号类型编码、脉冲重复周期、脉冲宽度、特征值和采样率。经过打包后，数据量为3.652 kb。单从数据量上就能看出本文使用的方法能够很好地减少传输数据量。同样按照上述实验方法进行实验，得到的结果如图5所示。

表1 雷达信号参数

图4 雷达信号数据传输耗时图

实验中，平均传输速率为219 kb/s，平均耗时0.173 6 s，达到了实时性条件。对比图4和图5，很清楚地看到，系统间传输特征值数据所耗时间远小于雷达信号数据传输耗时。说明本文提出的方法减少了系统间传递的数据量，大大减小数据传输时间。

图5 特征值数据传输耗时图

2.2 接收端复原信号对比实验

将实际的信号接收端复原的雷达信号时域波形与雷达信号发射端产生的信号进行对比，目的是为了验证本文提出的方法能够保证复原信号不失真。利用均方根误差来表示信号之间的差异，实验结果如图6所示。

图6 复原信号与源信号对比图

从图6可以看出，经过复原的信号与源信号相差无几，并使系统按照图3的两种信号传输方式进行仿真，最终得到的雷达信号的脉冲描述字相同，说明了该方法不会影响整个系统的仿真结果。

3 结论

本文根据透明计算的实现结构，提出一种实时信号级仿真系统的实现方法。将仿真系统中信号产生的硬件部分转移至信号接收端，利用所需产生信号的特征值来指导硬件在信号接收端产生所需信号。该方法减少了系统间传输的数据量，缩短传输时间，并达到与原系统相同的仿真效果，说明了该方法能够有效实现实时信号级仿真，具有一定的实际应用价值。