基于ICoSaMP重建的TDCS宽带压缩感知算法*
刘 洋,任清华,2,苏玉泽,王桂胜,徐兵政
(1.空军工程大学信息与导航学院,西安 710077;2.中国电子科技集团航天信息应用技术重点实验室,石家庄 050081)
0 引言
变换域通信系统(Transform Domain Communication System,TDCS)是认知无线电的候选技术之一,因其在低信噪比环境下具有良好的通信抗干扰性能以及灵活的频谱接入方式等优势受到广泛关注,具有良好的发展前景[1]。
由于TDCS具有很强的抗干扰性能,因此,非常适合于军事通信抗干扰领域,在电子对抗过程中敌对双方采取的干扰方式通常是有精确式干扰,包括单音干扰、多音干扰、窄带干扰和宽带干扰等方式,再加之TDCS的通信环境是一个低信噪比的宽带环境,其无线频谱具有明显的稀疏特性,因此,将压缩感知理论引入到TDCS宽带频谱感知的领域中。
目前国内在TDCS宽带压缩频谱感知领域研究较少,高成林[3]等人提出了一种基于时频二维压缩的MIMO-TDCS压缩感知信息反馈方法。李楠[4]等人针对TDCS宽带压缩感知使用随机性观测矩阵存在的局限,提出一种确定性嵌入式混沌序列-循环Toeplitz结构压缩感知观测矩阵构造方法。
压缩感知技术的关键问题就是如何快速精确地重建原始信号,之前的学者研究TDCS宽带压缩频谱感知所使用的重建算法都是基于已知稀疏度条件下的传统算法,如匹配追踪(MP:Matching Pursuit)算法、正交匹配追踪算法(OMP:Orthogonal Matching Pursuit)和压缩感知匹配追踪算法(CoSaMP:Compressive Sampling Matching Pursuit) 等 。 其 中CoSaMP算法是在OMP算法基础上的改进,添加了“回头检验”的思想,即将每次迭代选入支撑集的原子重新检验,符合条件则留在支撑集,反之删除不符合条件的原子。
针对上述问题,本文提出了一种盲稀疏度的ICoSaMP(Improved Compressive Sampling Matching Pursuit)算法。该算法利用频带占用率对信号的稀疏度进行估计,利用相邻两次迭代的残差之差小于某个阈值作为迭代终止条件,同时设置了残差比系数,降低系统噪声的影响。仿真结果表明,在相同信噪比和稀疏度条件下ICoSaMP算法相比于CoSaMP算法在重构概率方面有显著提高,在盲稀疏度条件下ICoSaMP算法的重建均方误差低于CoSaMP算法。
1 TDCS宽带频谱感知的模型描述
设TDCS的工作带宽为B,授权用户随机占用一部分频段,其余频段处于空闲状态,因此,宽带信号在频域具有一定的稀疏性。如图1所示。

图1 宽带频谱感知模型
在TDCS前端构建宽带压缩感知框架如图2所示。

图2 TDCS宽带压缩感知框架
AIC为模拟信息转换器,其以压缩感知理论为基础,可以直接对模拟信号边采样边压缩,从而得到离散的观测向量y为:


其中,F为N×N离散傅立叶变换矩阵,s为x的频谱,有K个非零值,并且K<M,被称作信号s的稀疏度。将式(2)代入式(1)中得

其中,Θ为M×N维观测矩阵,其需要满足约束等距特性(RIP)、零空间特性以及非相关性(Incoherence)等条件。
对于式(4)的求解,通常通过求解一个基于e0范数最小化的问题来重建频谱s,然后利用式(2)反解出信号x。

这种求解方式得到的解是最优的,但求解式(5)仍然是个NP难题。为此压缩感知理论采用的主要方法是将e0范数最小化问题转化为e1范数最小化问题,并且利用线性规划的思想来求解信号的重建[5]。文献[6]表明e1最小范数与e0最小范数在一定条件下具有等价性。因此,式(5)可以写为

目前解决这类凸优化问题主要使用贪婪算法,作为解决上述重建问题的快速有效算法,目前其主要包括匹配跟踪算法(MP)、分段匹配跟踪算法(StOMP)、正交匹配跟踪算法(OMP)和压缩感知匹配追踪算法(CoSaMP)等。
2 CoSaMP算法
与其他贪婪算法相比,CoSaMP算法的优点是在每次迭代的过程中能识别多个原子,从而能够快速收敛,同时添加了“回头检验”的思想,使得重构精度提高,避免了阈值选择的难题。其算法伪码如下。
输入:观测矩阵Θ,测量值y,稀疏度K。
1)m=m+1。
6)终止判决,若 m<K,则返回 1),否则执行 7)。
3 残差比阈值迭代终止条件设置
文献[7]针对传统迭代终止条件的不足,设计了一种新的残差比阈值迭代终止条件,解决了传统迭代终止条件在低信噪比下的不足。
首先,测量值y可以分解为

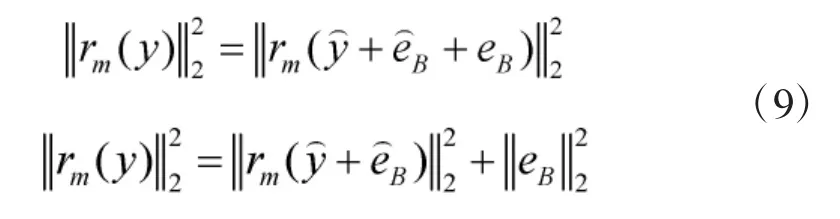


本文借鉴以上思想,对CoSaMP算法进行改进,提出了一种盲稀疏度的ICoSaMP算法。
4 盲稀疏度的ICoSaMP算法
4.1 算法分析
根据第2节针对CoSaMP算法的分析可知,其最大的缺陷就是需要知道信号稀疏度这样的先验信息,并且将其作为迭代次数,这使其在实际应用中的潜力大打折扣。第3节针对传统迭代终止条件的不足,设计了一种残差比阈值迭代终止条件,一定程度上克服了重建信号的过程在较低信噪比下的影响。
由以上分析,可将残差比阈值迭代终止条件应用到CoSaMP算法作为迭代终止条件而不依赖信号稀疏度K,即每迭代一次可以算出该次的残差比fm,再将其与设定的阈值θ进行比较,若fm<θ,则迭代停止,输出,否则继续迭代,直到fm<θ为止。对于CoSaMP算法在迭代过程中出现的稀疏度K,可以由该频段的占用情况进行估计。
在TDCS实际工程应用当中,信号的稀疏度很难获得,但是某个频段的占用率范围这个指标很容易求得,通常通过频谱检测仪器在一定区域内对某个频段进行检测获得,也可以对相关频谱管理部门进行问询来获得长期的调查统计结果,得到频带占用率范围之后就可以对信号的稀疏度进行一个粗略估计,例如美国相关研究部门对30 MHz~3 GHz这个频段内的频谱占用情况进行调查,其结果是5.2%~13.1%,因此,该频段的稀疏度范围为N×5.2%~N×13.1%,其中N为Nyquist采样频点数,稀疏度估计值K′在该范围取便可。
4.2 算法流程
ICoSaMP算法的伪码如下:
输入观测矩阵Θ,观测值y,稀疏度估计值K′
2)m=m+1。
7)迭代判决,如果 fm<θ,则执行 8),否则返回2),阈值的取值范围通常为0.1~0.5。
算法结束。
在改进后的ICoSaMP算法中,不需要知道信号稀疏度K这个先验信息,只需知道所研究频段的占用率即可,而这个参数在实际应用过程中很容易获得。该算法另一个优点是融合了残差比阈值迭代终止条件进而产生步骤7)迭代判决过程,代替了信号稀疏度这个迭代终止条件。解决了CoSaMP算法在TDCS盲稀疏度条件下无法精确重建信号的难题。
5 仿真分析
5.1 重建概率分析
为了验证改进后的ICoSaMP算法的重建效果,尤其是在TDCS这种较低信噪比的环境下ICoSaMP算法与其他算法在重建概率上的差异,利用MATLAB仿真平台进行验证,测量矩阵选用高斯随机测量矩阵,Nyquist采样频点数N=256,观测值数量M=128,频带占用率 η=10%,判决阈值 θ=0.2。
5.1.1 无噪条件下重建概率仿真分析
图3所表示的是在无噪条件下,OMP、ROMP、StOMP、CoSaMP和 ICoSaMP算法的重建效果对比图。

图3 无噪条件下不同算法的重建概率对比
由图3可知,ICoSaMP算法的重建概率曲线明显优于先前的CoSaMP算法,当信号稀疏度低于13时,各算法都能以接近百分之百的概率重建原始信号;信号稀疏度在15~40之间时,OMP和ROMP的重建概率开始明显下降,而CoSaMP和ICoSaMP算法依然能以接近百分之百的概率重建原始信号;而当稀疏度大于45时,CoSaMP和ICoSaMP算法的重建概率开始骤降,甚至低于先前的几个算法。这可能是由于CoSaMP和ICoSaMP算法在较高稀疏度下每次迭代需要选入更多原子作为支撑集进而产生过匹配的情况所致,因此,在较低稀疏度下,ICoSaMP算法重建效果优势明显。
5.1.2 有噪条件下重建概率仿真分析
TDCS传输系统的工作环境往往是低信噪比环境,因此,在较低信噪比环境下进行各重建算法的重建概率对比实验更具有实际意义。实验结果如图4所示。
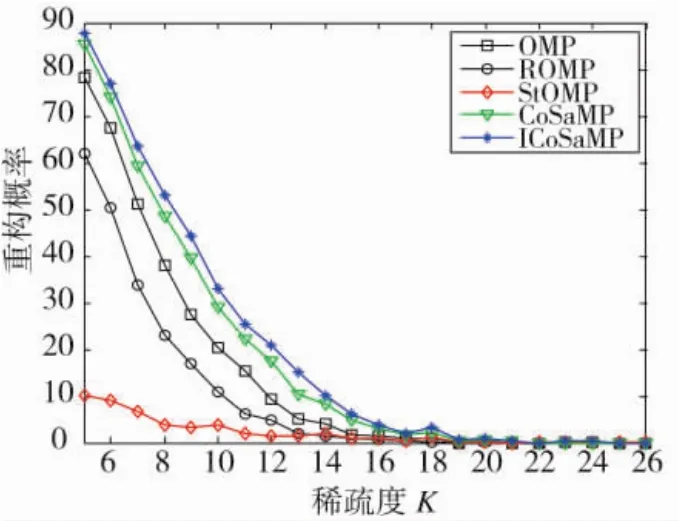
图4 不同算法在SNR=-1时的重建概率对比

图5 不同算法在SNR=0时的重建概率对比

图6 不同算法在SNR=1时的重建概率对比
图4~图6是几种算法在较低信噪比下重建概率与稀疏度的关系示意图,由图可知,各算法的重建概率在较低信噪比的环境下均受不同程度的影响,信噪比越低,重构概率越低。同时可以看出,ICoSaMP算法的重建概率曲线明显优于其他几种算法,通过计算可知,ICoSaMP算法在相同信噪比环境下的重建概率比CoSaMP算法高10%左右,这是由于ICoSaMP算法利用相邻两次迭代的残差之差以及残差比系数来削弱随机噪声的影响,进而提高自身的抗噪声性能。因此,ICoSaMP算法在较低信噪比环境下的优势更为明显。
5.2 重建效果仿真分析
以上实验验证了ICoSaMP算法在TDCS低信噪比环境下的重构性能明显优于先前的CoSaMP算法,下面验证ICoSaMP算法在盲稀疏度下的重建效果,稀疏度K=25,频谱占用率η=10%,其余条件不变,实验结果如图7、图8所示。

图7 原始信号

图8 两种算法的恢复信号对比
根据图7和图8可以直观地看到ICoSaMP算法和CoSaMP算法重建原始信号的效果基本一致,但是ICoSaMP算法是在未知稀疏度K的条件下对原始信号进行恢复。因此,ICoSaMP算法在盲稀度条件下优势已有体现。
5.3 均方误差(MSE)分析
为了检验ICoSaMP算法在TDCS低信噪比下的信号恢复精度,本文对OMP算法、CoSaMP算法和ICoSaMP算法进行均方误差(Mean Square Error,MSE)仿真分析,信号稀疏度K=25,频谱占用率η=10%,测量矩阵选高斯随机测量矩阵,Nyquist采样频点数N=256,观测值数量M=128,判决阈值θ=0.2。仿真结果如图9所示。

图9 不同算法的信号恢复MSE对比
图9给出了OMP算法、CoSaMP算法和ICoSaMP算法恢复原始信号的MSE值随信噪比变化的曲线。由于TDCS在较低信噪比下仍然具有良好的性能,因此,本文所选取的仿真环境是较低信噪比。由图9可知,不同算法恢复原始信号的MSE值都随着信噪比的增加而减小,且ICoSaMP算法的MSE始终略优于CoSaMP算法,这是由于ICoSaMP算法将相邻两次迭代的残差比阈值作为迭代终止条件,同时增加了残差比系数,这些改进措施使ICoSaMP算法具有一定的抗噪声性能,因此,在TDCS较低信噪比环境下恢复信号的精度高于CoSaMP算法,但另一方面,由于处于高噪声的仿真环境中,且噪声对重建算法的恢复精度有很大影响,因此,在高噪声环境下ICoSaMP算法与CoSaMP算法的恢复难度都很大,所以ICoSaMP算法的重建精度相比于CoSaMP算法是在可见范围内的提升。同样,图9中CoSaMP算法的MSE始终略优于OMP算法,这是由于CoSaMP算法是在OMP算法基础上通过添加“回头检验”的思想而进行改进的算法,因此,在相同条件下CoSaMP算法恢复信号的精度也就略高于OMP算法。
6 结论
在TDCS低信噪比环境下,信号在频域具有明显的稀疏特性,因此,利用压缩感知技术对TDCS前端的频谱环境进行感知。在实际的工程应用中,信号的稀疏度很难获得,而传统的CoSaMP算法在使用时必须要知道信号稀疏度这样一个先验信息。为此,本文利用频谱占用情况对信号的稀疏度进行估计,利用残差比阈值迭代终止条件对CoSaMP算法进行改进,提出了一种盲稀疏度的ICoSaMP算法。通过仿真实验,ICoSaMP算法相比于CoSaMP算法的重建精度更高,抗噪声性能越强,对于TDCS低信噪比下的宽带频谱感知具有重要意义。

