陆基GNSS干扰信号测向误差分析研究*

陈建华，陈树新，刘卓葳，黄 森

（空军工程大学信息与导航学院，西安 710077）

0 引言

随着“导航战”概念在军事对抗领域不断深入发展，针对全球卫星导航系统（GNSS）辅助作战这一战术形态，世界各国对卫星导航的干扰研究工作也在不断推进。目前我国北斗卫星导航系统（BDS）已经完成了亚太地区的部署并且为其提供导航、定位和授时的功能，军事和民用对其依赖程度日益增强。减轻地面环境噪声的影响，特别是消除人为干扰，是确保BDS用户端稳定工作的关键，而对GNSS干扰信号来波方向的测量则是实施测向定位的基础。然而目前L波段电磁环境比较复杂，除了GNSS信号，典型的还有900 MHz和1 800 MHz频段的移动通信信号。再者GNSS干扰信号功率较小，从测向体制上提高精度非常困难，这就给测向定位带来很大挑战。

目前在信号测向领域已经有很多研究成果，文献[5]基于雷达的大功率信号从目标跟踪角度研究了UHF频段雷达信号的测向精度，文献[6]针对通信信号从具体应用角度研究了GSM通信干扰信号的测向技术，文献[7-9]中提出根据角度变化率、相位变化率和相位差变化率来估计来波方向，从测向体制原理角度研究了测向精度，文献[10-12]从测向原理角度研究了2.4 GHz无线电波的测向误差，文献[13]针对测角可能得到异常误差给出了一系列抗异常误差定位算法。这些工作并没有从电波传播衰落角度对测向误差进行定性乃至定量地计算分析。

为使GNSS干扰信号测向所得的角度信息更加精确，为各类无源定位算法提供参考，同时为各类抗差算法提供典型异常误差的参考值，本文从电波传播的角度出发，基于环境噪声和大尺度衰落，分析了GNSS干扰电波在自然环境和阴影衰落下的功率衰减和信噪比变化情况，进而在相位法测向体制下计算了在上述环境中的测向误差。

1 GNSS干扰信号传播衰落分析

1.1 传播衰落要素

在电波传播过程中，造成衰落的因素有很多，例如自由空间传播、阴影、散射、反射、多普勒频移、大气吸收、云雾雨雪和太阳活动等影响。考虑到GNSS信号频率特点和测向需求，大气吸收、云雾雨雪以及太阳活动的影响微乎其微，故下文主要分析了自由空间传播和阴影衰落所造成的衰减。

1.1.1 自由空间传播

理想情况下，空间中的电波在传播过程中，能量是呈发散状向外辐射的，随着传播距离的增加，单位面积上所接收到的功率不断减小，如式（1）所示。

式中，Pr表示接收功率，Pt为发射功率，Gt和Gr分别为发射增益和接收增益，为电波波长，d为传播距离。

工程上一般用式（2）作功率预算的计算：

1.1.2 阴影衰落

除了自由空间传播衰减，GNSS干扰信号在传播过程中还可能会遇到各种障碍物的遮挡，由于这种遮挡造成衰减的因素是未知的，因此，采用统计的方法来描述。阴影衰落通常是一个乘性的且随时间缓慢变化的随机过程，其信号的接收功率可以用式（3）表示[14]。

式中，Lp表示平均路径损耗，Pt（t）是发射功率，Pψ（t）表示阴影衰落的随机过程。

对数正态阴影模型可以比较精确地刻画空间中无线电波接收功率的随机变化。其中，发射功率和接收功率的比值ψ被设为一个服从对数正态分布的随机变量，其概率密度函数为：

对数正态阴影衰落模型中的参数一般采用对数均值 μ[ψ]，在典型的微波环境中，σ[ψ]的变化范围一般为5 dB～12 dB。

1.2 典型传播模型分析

在实际的测向环境中，由于传播路径上存在各种不确定因素的影响，如地形起伏、地表水、地面建筑、植被和地球曲率的影响，电波传播的实际损耗是以上几种损耗的叠加。为了工程应用，人们建立了很多符合理论并且实用价值较高的电波传播预测模型，考虑到GNSS干扰源的工作频段、测向距离限制以及干扰源可能工作的地形环境，本文仅列举Longley-Rice模型和COST231-Hata修正模型。

1.2.1 Longley-Rice模型[15]

Longley-Rice模型在传统影响因素的基础上，还引入了极化方向、地形不规整度、地球表面折射率、地面电导率和相对介电常数等因素，在考虑电磁波本身传播特性的基础上，同时兼顾了传播环境的电气特性。该模型将整个传播路径上的总损耗分为自由空间传播损耗和其他损耗两部分：

式（5）中的Lf可通过式（2）计算得到，其他传播损耗Lo的计算如下：

式中，d为距离参数，对应自由空间传播距离；dLS为光滑地面距离，dx表示衍射与散射损耗相等的距离；Le、Led、Les分别表示自由空间下视距、衍射和散射时的传播损耗值，对应上述分析中的自由空间损耗、阴影和大气损耗；K1和K2为传播损耗系数，即对自由空间传播损耗的修正系数；md和ms分别为衍射和散射损耗系数，对应阴影衰落的损耗系数。

1.2.2 COST231-Hata修正模型

COST231-Hata模型[16]是在 Okumura-Hata模型的基础上，由欧洲研究委员会COST231工作组进一步扩展，将模型的频率适用上限从1.5 GHz提高到了2 GHz。COST231-Hata模型本质上是一个半经验半理论的传播模型，经过大量实验数据的检验，其经验公式如下：

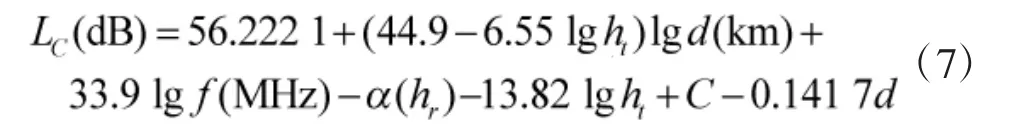
式中，ht和hr分别为发射和接收天线有效高度，单位为m；C为传播环境校正因子，密集大城市取3，其余环境取0；α（hr）是接收天线高度修正因子，其数值取决于环境因素：

郊区及中小城市：

大城市：

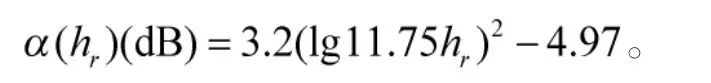
该模型的经验公式基于自由空间传播损耗公式，引入了天线高度影响因素，这符合信号衰减规律。环境校正因子C和接收天线高度修正因子α（hr）可以看作上述阴影衰落的影响参量。

1.2.3 模型选取

如上文所述，本文以近地对流层GNSS干扰信号的测向问题为研究对象，考虑到为了尽量减小误差，测向会选取地形较为平坦、视野较为开阔的地域作业，且测向距离一般会在数十公里级别，该问题没必要如Longley-Rice模型对各类参数进行细致的划分，如此细致的分析并不能提高最终的测向结果精度，反而增加了运算复杂度。而COST231-Hata修正模型正好满足解决该问题的需求，且运算量适中，可操作性强。故本文选择COST231-Hata修正模型来描述近地对流层GNSS干扰信号在传播过程中的衰减。

2 GNSS干扰源测向精度分析

2.1 测向方法

无线电测向的方法很多，例如振幅法、相位法和空间谱估计等，本节讨论相位法测向中的二单元干涉测向。

2.1.1 GNSS频谱特点

GNSS由于任务需求和技术特点的限制，其信号的载波频率都上升到了微波波段，典型GNSS工作波段如表1所示。

表1 典型GNSS工作频率

从表1中可知，GNSS信号载波绝大多数工作在L波段，目前已知的只有印度的区域卫星导航系统NAVIC有一个频点在S波段。以此为基础可以确定，GNSS干扰信号也应当工作这一频段，本文假设待测GNSS干扰信号工作在L波段。

2.1.2 相位法测向

各天线单元配置的位置不同，电波传播的路径不同，则传播时间也不同，最后电波在各天线单元上感应的电压之间形成相位差，相位法测向就是这个相位差进行测向。二单元干涉仪测向就是一种简单的相位法测向体制。

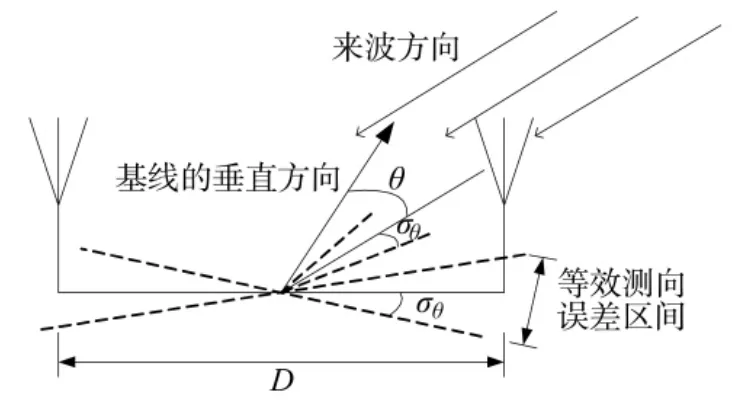
图1 二单元干涉仪二维测向

如图2所示，两个天线单元之间的连线称为测向基线，其间距D被称为天线孔径，一般用D与待测电波的波长的比值来衡量测向误差的精度，该比值一般取1～2，越大测向结果越精确[17]。

理想状况下，待测信号非常强，且不受任何干扰影响，如果忽略测向系统误差，假设该体制下相位模糊问题已经得到很好的解决，则测向结果可用下式表示：

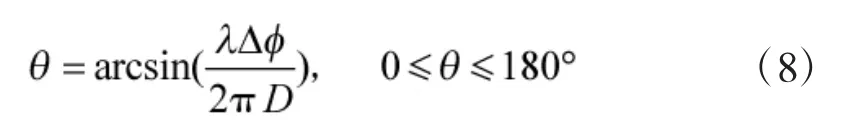
式中，Δφ表示两个天线单元所接收信号的相位差。

2.2 相位法测向精度分析

在实际测向作业中，电磁环境非常复杂，待测信号经过传播路径之后功率会发生很大的衰减，而且环境中存在自然噪声和有意无意的人为干扰，这些都会使测向结果产生偏差。据研究，这一偏差的大小跟该体制下所测得的Δφ的标准差σφ有关，其关系可用式（12）表示[18]。

在大信噪比条件下，两个天线单元所测得相位差的标准差σφ可以用下式来描述：

式中，S表示接收天线收到待测信号的功率，N是测向机所处环境总的噪声功率。

2.3 GNSS干扰源测向误差解析分析

根据上文分析，GNSS干扰源发出的干扰信号到达测向机接收端时的信噪比可以表示为：

将上式代入式（9）与式（10）可得：

上式就是在二单元干涉测向体制下测向误差受各因素影响的解析形式，可以看出在一定的信噪比条件下，干扰源有效发射功率和干扰信号传播损耗、测向环境噪声水平的比值决定了误差水平，在三角函数线性性质比较好的范围内测向误差的方差与之呈近似线性关系。

3 仿真分析

3.1 仿真1：传播衰落仿真

假设GNSS干扰设备发射天线有效高度为10m，测向设备接收天线有效高度分别设为5 m、10 m、15 m和20 m，以BDS电波衰减为仿真对象，结果如图2、图3所示。

图2 1 561 MHz电波传播信噪比变化

可以看出，L波段电波传播损耗随着距离增加而增加，与自由空间传播理论吻合，且频率越高损耗越大；接收天线接收到的电波传播损耗越小，且高度相差5 m，损耗差值大约为17 dB。

图3 不同接收天线传播损耗（1 561 MHz）

3.2 仿真2：测向误差仿真

假设周围不存在其他干扰测向设备正常工作的辐射源，GNSS干扰源以10 W的干扰功率稳定持续辐射干扰信号，其发射天线增益为12.1 dB[18]，环境中白噪声估计值为-141 dBW[18]（主瓣2 MHz带宽内），测向设备天线孔径取1，则在上文所分析的测向体制下的测向误差随信噪比变化规律如图4所示。

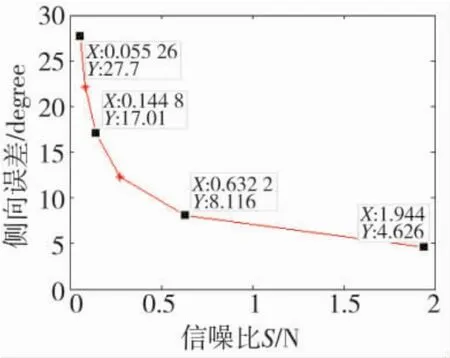
图4 1 561 MHz干扰信号测向误差随信噪比的变化

图3表明，GNSS干扰信号测向误差随着测向机前端信噪比的提高而降低，且在一定范围内呈现出近似指数下降。在本文研究的大信噪比条件下，测向误差最大不超过30°，这一结果可作为针对普通环境下GNSS测向误差研究的参考值。

测向天线与待测GNSS干扰源的距离15km[13]，路径损耗取值如表2所示，考虑不同测向天线高度对测向精度的影响，仿真结果如图5所示。

图5 测向误差与接收天线高度关系（1 561 MHz）

表2 1 561 MHz电波传播路径损耗（15km）

图4表明，随着测向天线有效高度的提升，相同条件下的测向误差近似指数趋势减小，这说明测向天线的高度是影响测向误差的重要原因，并且在一定范围内架高天线对提高测向精度具有重要意义，可以尝试通过飞机来完成这一需求，这一点很有启发意义。

4 结论

本文针对近地对流层GNSS干扰信号的测向问题，从干扰信号传播衰落要素出发，阐述了其与典型电波传播模型参数之间的关系，着重分析了GNSS干扰信号的频谱特点和相位法测向及其精度，推导了GNSS干扰信号信噪比与测向误差的定量关系，并且作了仿真分析，结论如下：

1）GNSS干扰信号测向误差随着测向机前端信噪比的提高而降低，且在一定范围内呈现出近似线性下降，在大信噪比条件下，测向误差最大不超过15°，这一结果可作为滤波算法和抗差估计研究中的参考值；

2）理论上测向距离越小越好，但是实际中由于干扰源方位未知和环境限制，测向距离不可能近，仿真结果表明信噪比大于0.5时测向误差已经趋于稳定，故测向距离选择在10 km左右最为经济；

3）随着测向天线有效高度的提升，测向误差近似指数趋势减小，说明测向天线的高度是影响测向误差的重要因素。但是地面上架高天线又有诸多限制，因此，可以考虑使用无人机作为测向平台。

针对以上结论和存在的问题，下一步工作应当着手考虑：干扰机工作模式多变，且存在信号多径和多普勒频移的测向误差；无人机测向平台飞行姿态的改变，引起干扰信号畸变甚至中断的情况；干扰源运动状态不断变化。