超低功耗短距离无线通信干扰源精准定位方法

唐 乐，赵吉祥

(1. 中国计量大学现代科技学院，浙江 义乌 310018；2. 中国计量大学信息工程学院，浙江 义乌 310018)

1 引言

无线通信技术在人们工作生活中扮演着关键的角色，低功耗与微型化是其主要优势。其中短距离无线传输在很多领域获得广泛应用，它可以解决由于环境约束而不利于有线布置的问题。此外还具有低成本、低功耗与对等通信的特点。由于传输距离相对较短，发射功率通常较低，因此需要扩大其应用范围。在传输过程中网络设备不必进行中转，接口设计与高层协议较为简便，资源管理一般会采用竞争方式。现阶段，短距离无线通信方式主要包括蓝牙、Wi-Fi以及超宽带技术。其中蓝牙传输范围在10～100米，可构建临时性对等连接；Wi-Fi虽安全性较低，但覆盖范围广，应用前景广阔；超宽带技术传输速度较快，在军事领域获得青睐。然而大部分无线通信技术还具有开放性的特征，导致网络中存在干扰源。为有效防止干扰攻击，众多学者展开相关研究，相继提出一系列干扰源定位方法。

文献[1]提出基于边界点拟合的干扰源定位方法。分析目标网络边界点与被干扰点的位置情况，选取最近的节点对，建立一组虚拟边界节点；基于该组节点通过最小二乘法拟合圆形式估计干扰范围，对虚拟点集合进行持续更新，并重新拟合干扰区域获取最后定位结果。文献[2]利用包络前沿特征对干扰源进行识别定位。将小波去噪与滑窗处理相结合完成信号滤波；通过互相关算法使接收信号和模板信号位置对齐；将包络上升沿差异幅值的平均值当做特性因子，采用K-means聚类方法完成干扰源识别与定位。

上述两种方法虽然对于不同种类无线通信都有较好的适应性，但只能在具有固定单个干扰源情况下才能实现精准定位。而在实际环境中，干扰源是移动的，且敌方一般会在无线传感网络中设置多个干扰源来达到理想的干扰效果。干扰范围不是简单几何区域，因此对定位造成一定困难。为此，本文引入灰色预测理论对干扰源进行准确定位。

2 基于灰色理论的无线通信干扰源定位

2.1 对数衰减模型构建

无线通信网络一般包含传感器节点、汇聚节点以及管理节点[3]三部分。传感器节点在目标范围内利用自组织形式收集信息并进行处理，此外还要与其它节点进行合作，共同完成其它工作。汇聚节点能够与外部网络相连，实现管理节点对网络的访问与管理。

为实现干扰源准确定位，本文对网络模型做出下述假设。

1)所有节点都处于静止状态[4]。布置完网络后，节点不再移动，即网络运行过程中，节点位置固定。

2)节点具体位置是已知的，每个节点都有自己的位置信息。

3)网络运行过程中，节点能够获取接收信号功率，并将其当做网络信息进行通信。

4)节点能够在网络运行时，结合具体情况更新邻居节点列表。

在无线通信过程中，由于会出现路径损耗[5]现象，导致信号强度逐渐减小，且和信号传输距离存在函数关系。针对干扰信号，利用对数衰减模型对无线通信网络进行表示。无线通信符合下述公式要求。设定Pt表示原始发射功率，Pf代表出现一定损耗后的功率，Xσ为其它损耗，在距干扰源d距离处，节点接收功率等于Pf与变量Xσ的和，其表达式如下。

Pt=Pf+Xσ

(1)

Pf=Pt+K-10ηlog10(d)

(2)

式中，Xσ属于一个随机变量，K是一个与天线特性相关的常数，η代表消耗指数。通常情况下无线通信能量随路径损耗情况符合上述对数衰减模型。

2.2 节点干扰判断

本文将干扰所在区域近似看做以干扰源为中心的圆形范围。与干扰源距离不同，通信受到干扰情况也不同。位置越接近干扰源，受到干扰越严重，甚至无法保持正常通信，导致网络黑洞；而没有受到干扰的节点，通信能力不会受到影响。因此，本文结合节点受干扰状况，利用信噪比衡量通信受到的干扰程度[6]，并对节点做如下划分。

Nj表示遭到干扰节点：此节点在干扰区域内，不能和邻居节点进行正常通信，无法出现在通信网络拓扑结构中。

Nb表示边界节点：该节点处于干扰区域边缘部分，会受到较小干扰，能保证部分网络连接。邻居列表中会减少一些遭到干扰的节点，这些节点在通信网络中呈现出环形分布，处于最大干扰区域处。

Nu表示正常节点：在干扰范围之外，能够保证正常通信，邻居列表[7]始终不变。

当网络遭到不同程度干扰后，邻居节点列表会出现一定改变，节点能够结合网络信息来判断是否遭到干扰，其不同情况下的表达式为

Nj={nj|SNRiu<γ0，∇i∈n}

(3)

Nb={nb|∃i∈n，SNRiu>γ0}

(4)

Nu={nu|SNRiu>γ0，∇i∈n}

(5)

2.3 干扰源区域划分

根据上述出现的不同干扰情况，利用网格聚类方法明确干扰源数量，并对其所在区域进行初步划分。该方法主要分为空间网格化与网格单元聚类[8]两个步骤，详细描述如下所示。

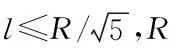
步骤二：将不同节点之间存在的欧式距离当做聚类依据，假定Qi，j表示传感器网路第i行、第j列的网格单元，cidi，j代表Qi，j的类别标识符，sidi，j属于Qi，j的搜索标示符号。则实现网格聚类的步骤如下：

1)将全部网格单元Qi，j类别标识符号cidi，j与搜索标识符号sidi，j都设置等于零，类临时符号k设为1。

2)遍历全部网格单元Qi，j，如果Qi，j不是空集，且满足cidi，j=0，则设置cidi，j=k、sidi，j=1、k=k+1。

3)遍历Qi，j的全部邻居单元Qm，n，Qm，n不属于空集，且sidi，j=0。

4)如果cidm，n≠0，则令sidm，n=1，此时回到步骤3)继续执行。

5)反之，如果∀Pr∈Qi，j，∀Ps∈Qm，n，且符合Pr与Ps之间存在的距离小于或等于设置距离ε，令cidm，n=cidi，j。

6)反之，将Qm，n中全部和Qi，j中节点距离不高于设置距离ε的节点Ps引入Qi，j内。

7)完成遍历后，将全部和cid相同的网格单元分为同一类，并输出最终聚类结果。

2.4 干扰源精准定位

2.4.1 二次多项式干扰源运动模型

在确定每个干扰源所在区域后，针对运动干扰源，构建二次多项式运动模型。该模型表示在固定时间段内结合定位坐标、速度与加速度构建干扰源运动模型[9]。

针对干扰源运动路线建模，假定干扰源在x与y方向的运动模型分别为mx和my，t时间点上模型参数矢量表示为axt与ayt，则运动模型描述为

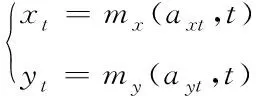
(6)

式(6)属于时变模型，运动参量会随干扰源移动而发生改变。由于节点采样时间较短，参数不会出现较大变化，因此结合运动学理论，将上述运动模型变换为二次多项式干扰源运动模型，其表达式为

(7)

式中，ρxk与ρyk是x与y方向干扰源预测模型，xk与yk表示tk时间点干扰源具体坐标，vxk、vyk与axk、ayk分别代表干扰源在x与y方向的速度与加速度分量。

将式(6)与(7)进行对比，能够获得模型参数矢量axk=[xk，vxk，1/2axk]，ayk=[yk，vyk，1/2ayk]。

如果干扰源加速度固定，通过及时更新拟合数据即可抑制定位误差，从而提高运动模型对干扰源运动的自适应性。

2.4.2 基于灰色理论的精准定位

在获得每个干扰源二次多项式运动模型后，利用灰色理论对干扰源进行精准定位。灰色预测属于一种对具有不确定因素进行预测的方式，经过判断不同因素发展趋势，对其做关联分析，寻找变换规律，形成数据序列，并构建微分方程，预测事物未来发展趋势，从而获得目标精准位置。下面对定位过程进行描述。

假设原始序列表示为

{X(0)=X(0)(1)，X(0)(2)…，X(0)(n)}

(8)

如果k′代表数据序列时刻，初始数据属于0次累计数据，则初始数据每次累计序列表示为

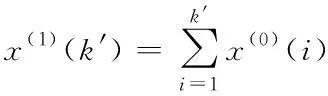
(9)

经过n此累计的序列为

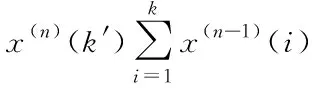
(10)

通过r次累计数据序列x(r)(k)的O次数据累减表示为

a(0)(x(r)(k))=x(r)(k)

(11)

则n次数据累减定义为

a(n)(x(r)(k))=a(n-1)x(r)(k)-a(n-1)(x(r)(k-1))

(12)

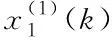
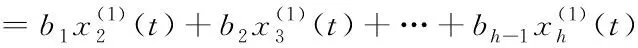
(13)

上述方程被称作GF(n，h)模型，若n=1且h=1，GF(n，h)将退化为GF(1，1)模型。它可以在已知一定历史数据前提下预测系统的未来发展趋势。

利用上述微分方程的干扰源进行定位，分为以下步骤

步骤一：对位置序列X(0)做准光滑检验，并假设

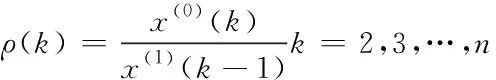
(14)

如果符合ρ(k)<1、ρ(k)∈[0，ε](ε<0.5)，则ρ(k)表现出递减趋势，此时称X(0)是准光滑序列，则X(1)具备准指数特征。反之利用下述公式做一阶弱化处理[11]。

步骤二：通过上步可知，根据干扰源位置信息累加生成的序列X(1)存在指数增长规律，所以能认为序列X(1)符合以下一阶线性微分方程

(15)

对上述方程求解得到

(16)

式中

(17)

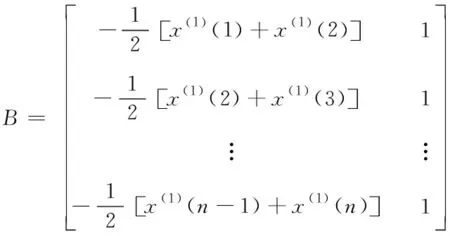
(18)

(19)

步骤三：构建灰色预测模型，根据微分方程(16)获得累加数列X(1)的预测模型

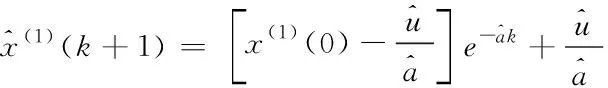
(20)

若X(1)是X(0)经过一阶弱化处理获得的数列，则根据式(16)进行一阶弱化还原

(21)

反之，进行累减还原，获得X(0)的预测模型为

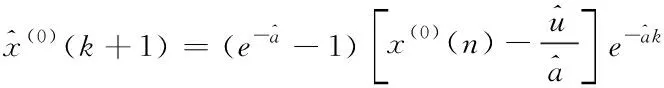
(22)

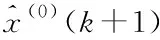
3 仿真分析

为验证本文提出的超低功耗短距离无线通信干扰源精准定位方法的可行性，利用Matlab 2018a仿真工具搭建一个100m×100m仿真平台，在此区域中随机设置节点。假设节点通信半径为30m，任意一个节点上均布置全向天线，能够和自身通信范围内的邻居节点实现通信。将干扰源放置在此平台中，随机撒播完节点后在干扰环境下利用文献[1]、文献[2]与本文方法对干扰源进行定位。当干扰源较为单一且位置不变时，将定位误差与根均方差当做评价定位精度的量化指标。两个指标定义分别如下所示：

(23)

2)根均方差：干扰源定位误差平方和的平均值，表示算法定位和实际位置的偏移程度。

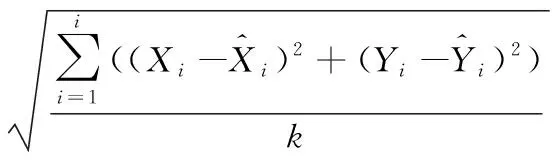
(24)

每个算法分别运行7次，则在单一干扰源情况下定位精度对比情况如图1和图2所示。

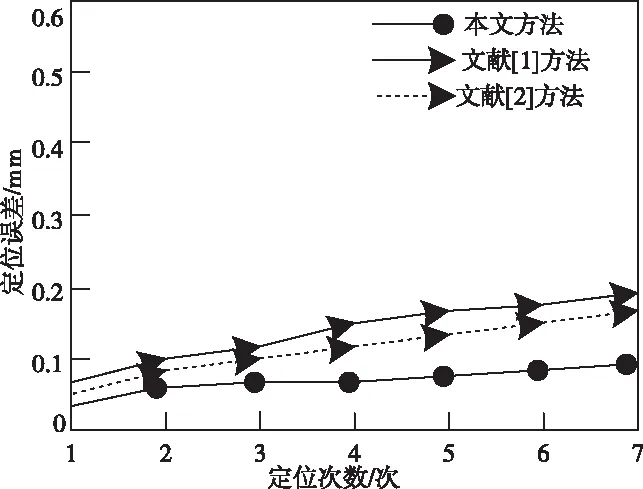
图1 不同方法定位误差对比图

图2 不同方法跟均方差对比图

由图1和图2可以看出，三种方法在单一干扰源情况下，定位误差均较低，但是所提方法定位误差与根均方差最低，全面反映出该方法定位精度高，获得的干扰源位置与实际位置偏差较小。这是因为本文利用网格聚类方法确定干扰源数量，明确单个干扰源所在区域，对传感器节点密度非常敏感，因此提高了定位精度。

在多干扰源直线和曲线两种运动下，对本文方法、文献[1]方法和文献[2]方法的超低功耗短距离无线通信干扰源进行定位，定位结果如图3和图4所示。

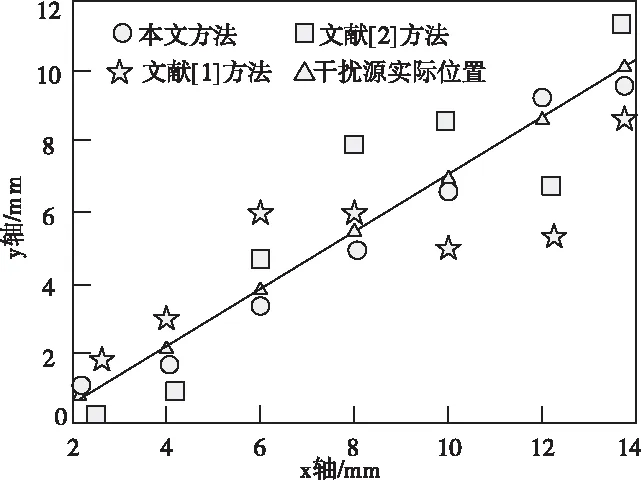
图3 多干扰源直线运动定位图

图4 多干扰源曲线运动定位图

从图3与图4可以可知，无论多干扰源进行直线或曲线运动，本文定位方法都优于其它方法。这是因为本文方法对干扰源进行了运动建模，通过灰色理论预测干扰源运动位置，从而实现了精准定位。

4 结论

为满足超低功耗短距离无线通信网络安全要求，本文提出一种基于灰色理论的干扰源定位算法。构建干扰源运动模型，对原始数据进行累加处理，寻找系统变动规律，实现干扰源定位。仿真结果表明，该方法无论针对单一还是运动的干扰源都表现出较高的定位精度。由于本文提出的聚类算法在聚类过程中有时会存在误差，所以，对聚类方法需要进行进一步研究，设计更加稳定、精准的聚类过程，对干扰源定位具有重要意义。