直升机双旋翼气流纵向稳定性恢复方法仿真

郎娟芳

(空军工程大学航空机务士官学校，河南 信阳 464000)

1 引言

双旋翼直升机的基本结构特征是拥有两幅完全相同的旋翼[1]，以一上一下的结构形式安装在同一个旋翼轴上，两个旋翼之间保持安全间距。这种双旋翼结构直升机在使用过程中产生的扭矩大小相等，且方向相反，能够在飞行过程中进行相互抵消，由此可以通过控制两旋翼之间的总距来操纵直升机的飞行航向[2]。然而直升机在飞行过程中会受到高空的气流影响，横向气流会对直升机产生阻力，而纵向气流会影响直升机飞行的稳定性，当直升机双旋翼发生稳定偏移时，需要通过控制器以最快的时间使其恢复稳定状态，否则就可能会引发飞行事故，甚至发生空难。

在进行直升机双旋翼气流纵向稳定性恢复的过程中，需要按照偏移情况提供稳定机械力，进而达到恢复稳定的效果，因此稳定性恢复控制设备需要检测主直升机当下的飞行状态，以及受力情况，及时的生成恢复驱动程序，并计算出具体的恢复参数[3]。传统的直升机稳定性恢复方法包括：基于自适应的稳定恢复、基于模糊控制的稳定恢复以及基于非线性遥控的稳定性恢复方法。这三种传统的方法分别通过自适应算法、模糊矩阵以及非线性遥控算法实现直升机双旋翼的快速稳定。

然而经过长时间的应用发现，传统稳定性恢复方法存在着恢复时间长的问题，为此提出针对直升机双旋翼气流纵向稳定性恢复方法，以达到加快恢复速度的目的。

2 双旋翼气流纵向稳定性恢复方法设计

2.1 建立直升机运动坐标系

将直升机的运动情况看成是六个自由度的刚体运动，即绕三个轴的转动和重心沿三个轴的线运动[4-5]。在不考虑直升机双旋翼弹性振动以及变形情况下，以直升机的重心为原点建立坐标系，坐标系建立结果如图1所示。

图1 直升机运动坐标系

由图1(a)可知，直升机的机体坐标系的纵轴Ox在直升机对称平面内，且规定指向机头的方向为正，竖轴Oz通过重心且竖直向下；横轴Oy通过重心，与平面Oxz垂直，右旋旋翼指向右方向为正，与左旋旋翼的正方向相反，在该坐标系下可以对直升机双旋翼的悬停状态进行分析。当直升机呈现飞行状态，会产生对应的偏向角，因此需要建立飞行状态下的速度坐标系，如图1(b)所示。定义直升机的机身迎角为α，飞行速度为v，在这种飞行状态下，以机体轴Ox作为飞行速度v上的正方向，定义侧滑角β是飞行速度v与无人机对称平面之间的夹角，且飞行速度v位于X轴右侧的正方向[6]。

2.2 构建直升机双旋翼状态方程

通过分析双旋翼悬停状态，在坐标系上构建直升机双旋翼运动状态方程，并加以分析双旋翼的运行状态。当直升机处于快速飞行状态时，双旋翼均处于较大后行边反流区，承受大量的阻力[7-8]。前行边的气流从桨叶的前缘位置向后移动，逐渐向后缘位置靠近，并在后缘处形成脱体涡，反流区气动情况如图2所示。

图2 反流区气动示意图

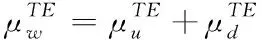
(1)

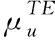
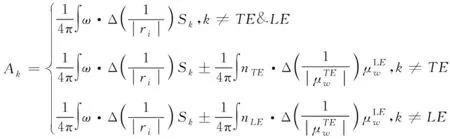
(2)

式中，nTE与nLE为后缘与前缘的法向矢量，而ri为后缘或前缘的位置矢量，当i取值为k时，则表示第k个面元的位置矢量。另外，Sk表示的是第k个单元面积，ω表示运行方向角。综合偶极子的影响系数，可以得出直升机双旋翼桨叶偶极子的求解方程

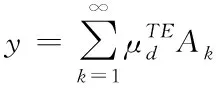
(3)

当求解出的y值小于0时，判定直升机处于悬停状态；若y∈[0，1]，则处于慢速飞行状态，若y值大于1，则直升机处于快速飞行状态。由此可以得出直升机双旋翼的运动状态方程为

Y=Cx+Dy

(4)

式中，C与D为参数系数。

2.3 双旋翼气流纵向动力计算

直升机双旋翼在飞行过程中除了机身施加的支持力外，还受到自身的重力G，气流产生的气动力Fwj、后向力FH、拉力T以及侧向力FS，双旋翼在总方向上的受力分析情况如图3所示。

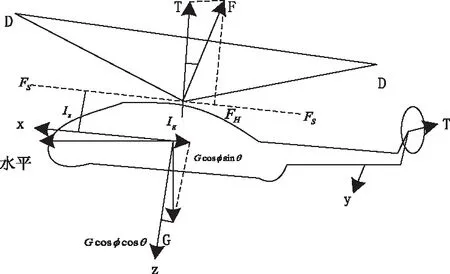
图3 双旋翼纵向受力分析示意图

这些力作用在直升机的双旋翼上引起了对中心的俯仰、横滚以及偏航力矩。因此分别从旋翼载荷情况、纵向气流力矩两个方面得出气流纵向动力值。针对直升机双旋翼的桨叶进行受力分析，分析结果如图4所示。

图4 桨叶剖面受力示意图

从图中可以看出，双旋翼桨叶经过气流的影响，主要受到气流施加的升力和阻力。其中升力用dL表示，其计算公式如下

(5)

式中，b为双旋翼的弦长，Cl为双旋翼的升力系数，ρ为气流密度。则阻力dD的计算公式为

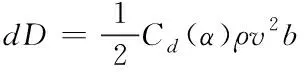
(6)

式中，Cd为双旋翼的阻力系数。根据能量守恒定律来判断dL与dD的稳定性，若dL与dD大小相等且方向相反，则直升机双旋翼气流纵向呈现稳定状态，无需进行稳定性恢复调整。若得出dL大于dD，则直升机双旋翼气流纵向向上偏移，需要通过恢复程序向下进行稳定恢复，若得出dL小于dD，则进行反方向恢复调整。

2.4 实现稳定恢复方法

在安装稳定恢复控制器的基础上，根据气流纵向动力的计算和判断结果，求出双旋翼恢复稳定的配平量，进而形成稳定恢复程序，分别通过驱动急拉杆/急推杆和转弯电压稳定恢复实现直升机双旋翼气流纵向的快速稳定恢复。

2.4.1 安装稳定恢复控制器

通过在直升机上安装双旋翼气流纵向稳定性恢复控制器来生成对应的稳定性恢复程序，通过控制器将生成的程序传输到直升机的控制中心，通过调整直升机的机械设备实现稳定性恢复。安装的稳定性恢复控制器的结构如图5所示。

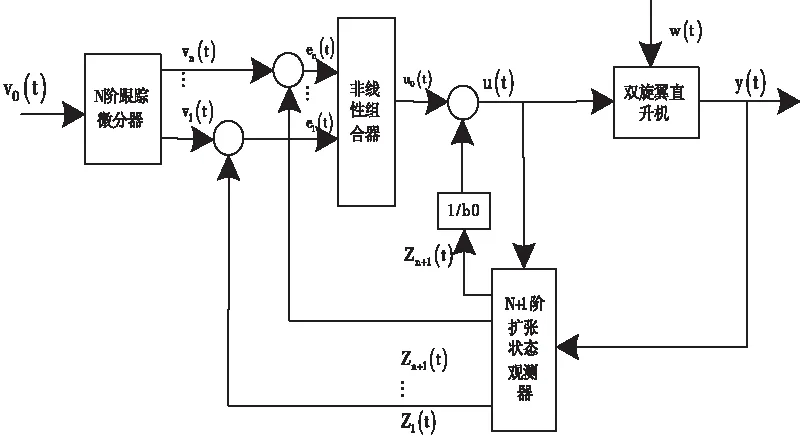
图5 自抗扰稳定恢复控制器结构图

从图中的结构可以看出，整个稳定恢复控制器由跟踪微分器、扩桩状态观测器以及非线性反馈律三部分组成。在三个组成部分的协调作用下计算恢复强度，并生成稳定性恢复程序。

2.4.2 气流压缩分离

按照生成的稳定性恢复程序，确定气流的分离点f，求出分离系数η的值。

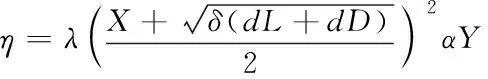
(7)

式中，δ为沿弦向从前缘机器的无量纲分离点的位置系数，λ为法向力斜率。在标准大气压下，气流的升力曲线斜率可以取常数2π。而直升机双旋翼气流纵向稳定性恢复的气流分离点的位置选取与直升机运动状态的迎角α有关，因此通过对迎角的分类得出气流分离点的具体位置计算公式

(8)

式中αz为零升迎角，参数0.7为迎角的失速值，αH表示失速角的临界值，S1为稳定特性参数。在选择好分离位置的基础上，对分离强度C进行计算，计算公式如下

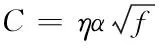
(9)

在程序执行过程中，直升机双旋翼的f位置上，将分离强度C对气流进行压缩分离，降低气流对双旋翼的作用力。

2.4.3 驱动急拉杆/急推杆

驱动急拉杆/急推杆是在纵向对称面内进行恢复控制，急拉杆是用来向上进行稳定性恢复调整，而急推杆用来向下进行稳定恢复调整。驱动拉杆与纵向恢复变化情况如图6所示。

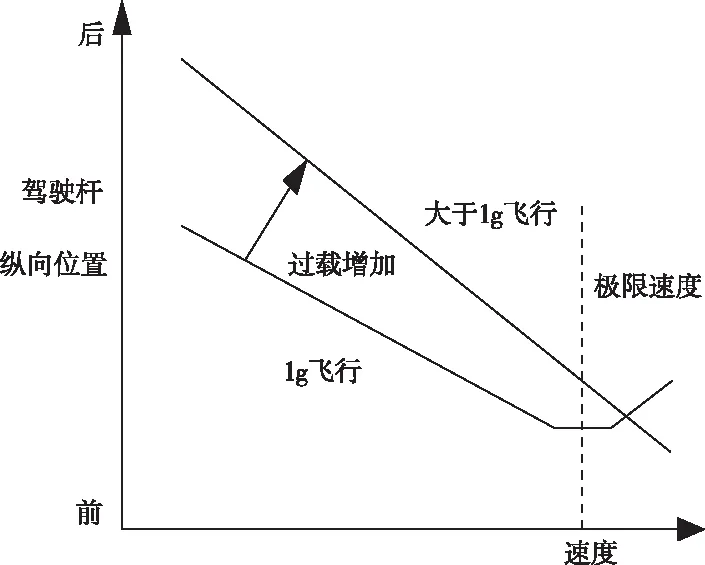
图6 驱动急拉杆/急推杆与纵向位移的变化关系

通过对急拉杆/急推杆的驱动，可以及时准确的对直升机双旋翼的角度进行调整，实现角度方向上的稳定恢复。

2.4.4 电压稳定恢复

直升机的过载和倾斜角有关，因此可以使用转弯飞行的方法来恢复直升机双旋翼气流纵向的稳定性。在转弯的过程中，需要保证电压稳定，为直升机转弯提供足够的动力支持。假设将直升机两个旋翼电机上的电压表示为V0和V′0，那么控制器输出的电压值为

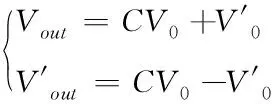
(10)

将式(10)中的方程组联立，即可得出每一个旋翼的电压为

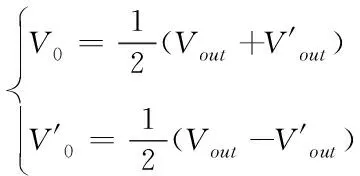
(11)

上式计算结果即为发给直升机双旋翼的最终电压控制信号值。

综上所述，结合稳定恢复的气流分离参量、急拉杆驱动参量以及转弯电压参量，实现直升机双旋翼气流纵向稳定性的恢复方法。对直升机双旋翼气流纵向稳定性恢复方法进行设计，设计过程如图7所示。

图7 稳定性恢复方法流程图

从图中可以看出，首先对直升机双旋翼的运行状态进行分析，同时对影响直升机双旋翼稳定性的纵向气流情况进行计算。根据分析计算得出的结果生成对应的控制程序，即对主控程序求解，得出距离的稳定性恢复参数值，最终通过对直升机上机械设备的驱动与控制实现直升机双旋翼气流纵向稳定性的快速恢复。

3 仿真分析

3.1 仿真对象

本文以ANSYS为仿真平台建立微型共轴双旋翼的有限元模型，控制网格总体数目并保证旋翼模型周围的网格密度，整个计算域的网格总 数为371585。直升机的参数如表1所示。

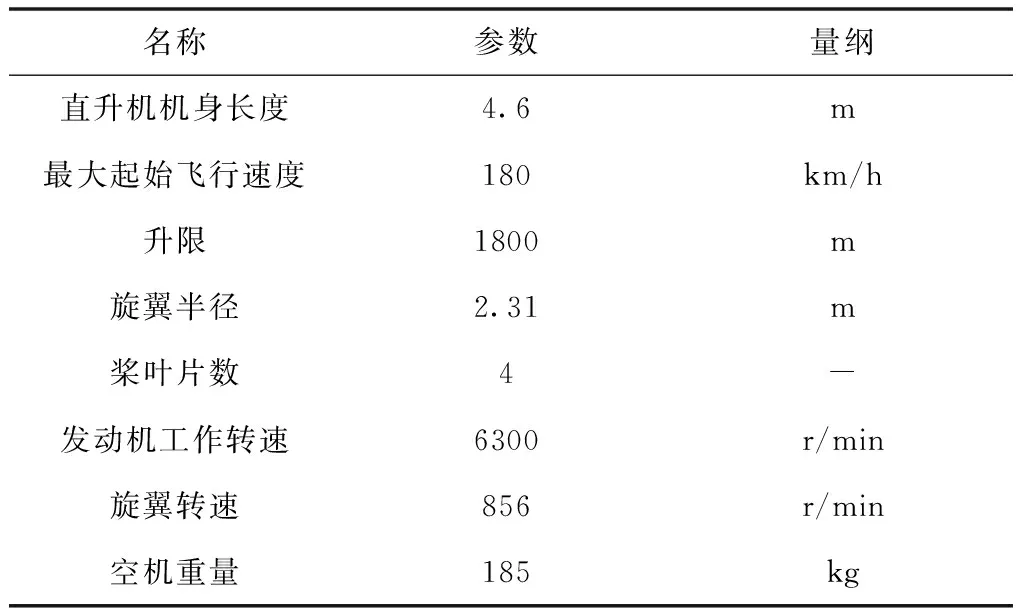
表1 仿真对象构建数据

3.2 流线分析

在仿真环境中模拟气流，气流的生成装置为鼓风机，模拟实际鼓风机的制风强度。将气流强度分别固定为5NL/min、10NL/min、20NL/min和30NL/min，编写随机程序控制气流方向，充分反映直升机的实际飞行环境。为能直观地从流场结构等细节来观察共轴双旋翼周围及重叠区域的流场特点，各间距下的径向流线分布如图8所示。

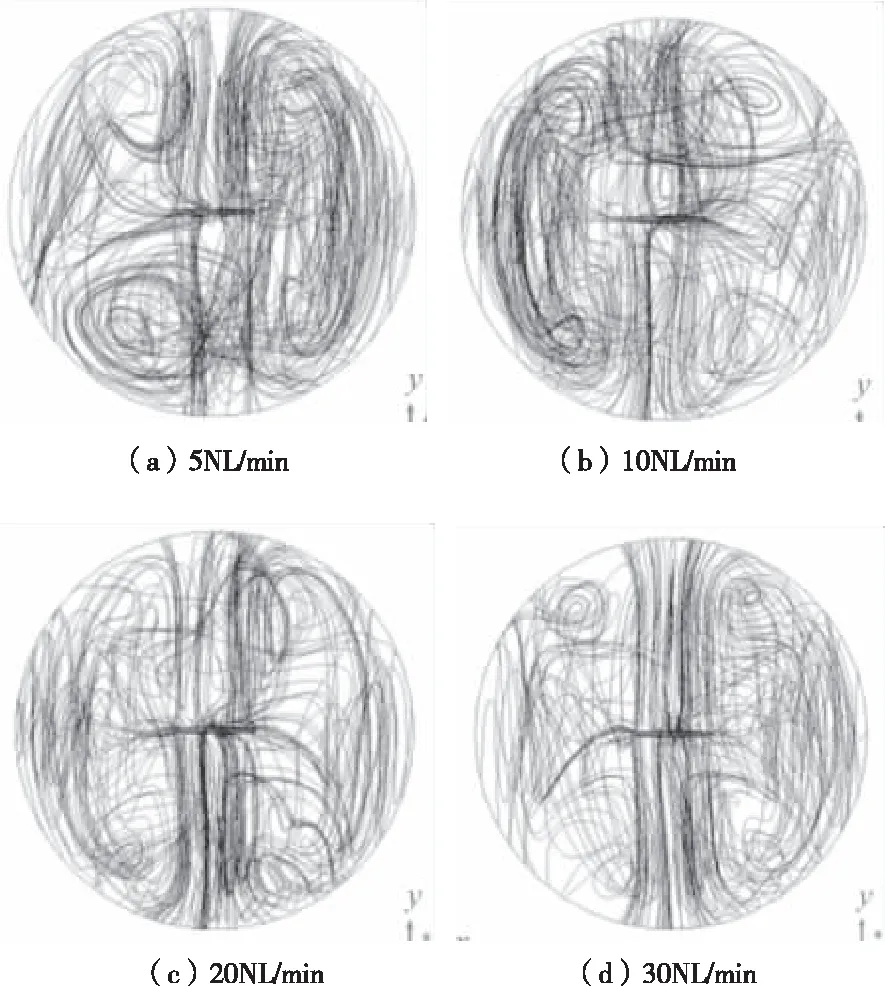
图8 径向流线分布

从图中可明显看出由于旋翼间的气动干扰，旋翼附近产生的涡流使得流线周向发散，间距较小时涡流相互作用强烈，当涡流干扰发生在旋翼附近时会对共轴升力和功耗产生影响。双旋翼重叠区域的流场存在耦合干扰，涡流周向流动明显。随着间距增大，上下旋翼间的气动干扰减弱。小间距内强烈的气流耦合一定程度上提高了旋翼系统的性能。

3.3 稳定性恢复时间对比

在小间距径向流线分布前提下，同时启动实验环境中的气流，直升机双旋翼上受力平衡，且双旋翼稳定运动作为稳定性恢复的标准，以双旋翼失衡为时间起点，恢复稳定为时间终点，记录两种方法的稳定性恢复控制时间，并将两种稳定性恢复方法的恢复时间进行对比。通过时间的统计，可以得出两种稳定性恢复方法的恢复时间对比结果如图9所示。

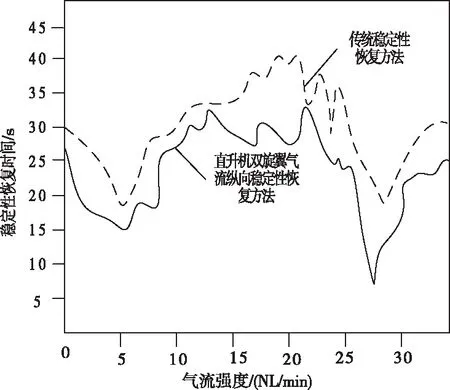
图9 仿真结果对比曲线

从图中可以看出，无论气流强度如何，设计出的稳定性恢复方法消耗的时间始终低于传统方法。经过计算，传统方法进行恢复处理消耗的平均时间为33.84s，而设计出的直升机双旋翼气流纵向稳定性恢复方法的平均时间消耗为19.93s，比传统方法节省13.91s，说明本文方法的稳定性恢复时间较短。

3.4 上、下旋翼截面载荷

上、下旋翼气动干扰对桨盘诱导速度和非定常气动载荷影响明显。因此对上、下旋翼截面载荷进行分析。如图10所示。

图10 上、下旋翼截面载荷

由上图可以看出，随着方位角的变化，上、下旋翼截面法向升力系数呈现上下波动，与流体力学计算结果相吻合，证明本文方法对于截面荷载的计算结果较为准确，从而保证了直升机双旋翼气流纵向稳定性快速恢复。

4 结束语

直升机双旋翼具有十分复杂的动力学特征，能够实现多变的飞行姿态。通过直升机双旋翼气流纵向稳定性恢复方法的仿真研究，进一步为直升机双旋翼提供飞行的安全保障。尽管设计出的稳定性恢复方法具有足够的有效性，但该方法只考虑了气流对直升机双旋翼的纵向影响，而在设计中没有考虑到一些横向的、以及倾斜方向的气流影响元素，因此在今后的工作当中需要针对该方面进行进一步研究。